资金短缺零售商促销下供应链的协调

代建生 刘新愿

(昆明理工大学 管理与经济学院,云南 昆明 650093)

0 引言

中小企业在我国经济发展中起着重要作用,截至2015年底,我国99%以上的企业是中小企业,他们创造了60%以上的GDP及50%的税收收入[1]。中小企业普遍面临资金短缺,这一问题严重制约了企业的健康发展,甚至导致企业破产。2019年上半年美国多家零售商因破产关闭旗下门店,全美零售行业关店数量超过7000家[2]。

供应链是物流和资金流的统一体,物流和资金流相向流动。节点企业的资金短缺阻碍供应链的交易活动,导致供应链效率低下。中小企业由于资金薄弱,资本流动性差,对经营风险的抵抗力较小,难以获得银行等外部金融机构的融资[1]。为了改善供应链的运营绩效,伴随着节点企业的交易活动,贸易融资应运而生。作为一种短期的贸易信用方式,延迟支付能缓解购货商暂时性的资金周转困难,改善供应链的运营绩效[3],因而广泛存在于商业活动中。截至2018年末,我国规模以上工业企业应收账款额高达14.3万亿元,平均回收期为47.4天[4]。

在市场经济下,促销是赢得市场竞争的重要手段。由于延迟支付只能缓解商品采购的资金短缺问题,不能解决促销资金短缺问题,因此,在零售商促销下,其采购决策面临更大的限制,供应链的协调也面临更大的挑战。直觉上,零售商的资金短缺问题越严重,其运营决策受到的限制越大,供应链的协调也愈加困难。已有一些文献研究了资金短缺对零售商运营策略的影响,结果表明:资金短缺零售商的订货量低于资金充足下的最优水平[5-6]。还有一些文献探讨了资金短缺对供应链协调的影响,指出在资金充足下有效的契约安排在资金短缺下未必有效,比如,在资金充足下,收益共享契约能协调供应链[7],但在资金短缺下,这一结论并非总是成立的[8-9]。尽管如此,鲜有文献在“零售商促销且融资途径仅限贸易融资”这一背景下讨论资金短缺对零售商运营策略及供应链协调的影响,尤其缺少探讨“资金短缺严重程度对零售商策略及渠道协调影响”的文献。本文拟对上述问题进行讨论,尤其关注收益共享契约能否协调供应链以及资金短缺程度对契约协调的影响问题。

本文考虑资金充足的供应商和资金短缺的零售商组建的供应链,供应商提供延迟支付政策,将报童商品销售给零售商,零售商实施促销努力(比如优惠券、赠品、促销广告、宣传标语、艺人促销活动等),并以商品销售收入为限承担延迟支付货款的偿还责任。供应商分担零售商的促销成本。特别地,本文限定在以下背景下进行讨论:除了贸易融资,零售商没有其它融资渠道。在这一背景下,促销资金短缺问题不能通过融资渠道解决,这是本文区别于现有的资金约束下的运营管理文献的一个重要特征。本文刻画了零售商的订货及促销策略,设计了能协调供应链的收益共享和促销成本分担机制。

本文还讨论了一个相关问题:如何度量资金的稀缺程度?直觉上,可以用初始资金这一指标进行度量,但这一指标存在以下问题。首先,初始资金的多寡只能反映企业拥有的资金状况,包括充裕和短缺状况;由于缺乏比较的标准,我们不能根据初始资金的大小判断资金状况是否短缺。其次,仅仅使用初始资金这一指标不能完全衡量资金短缺的程度,难以确定资金是极其短缺还是相对不足。最后,作为一个绝对指标,初始资金忽略了企业经营规模的大小,难以对两个或多个企业资金稀缺的程度进行比较。本文构造了一个相对指标(实施最优策略要求的最低资金与初始资金的差与最优策略得以实施所要求的资金之比)来衡量资金的稀缺程度。

下面对相关文献进行评述。本文与以下三类文献相关,其中第一类文献是促销影响需求下供应链契约协调文献,相关研究表明:在零售商促销下,供应商通过分担促销(广告)成本,能为零售商的促销努力提供额外的激励[10],并最终导致合作双方实现双赢[11]。特别地,借助促销(广告)成本分担机制,收益共享或回购契约能够协调供应链[12-14]。部分文献还对上下游企业同时开展合作促销下的协调问题进行了研究[15],结果表明:通过相互分摊对方的广告费用,可以实现供应链的协调[16];特别地,收益共享契约能协调供应链[17]。上述文献均在资金充足下进行研究,而本文在资金短缺下进行讨论。本文构造的协调契约包含了促销成本分担机制,其中两个协调机制也适用于资金充足情形,研究表明:资金短缺限制了促销成本分担比例的取值范围(在资金充足下,这一比例可取0至1的任意数值),且资金短缺越严重,促销成本分担比例的取值范围越小。

第二类文献关注零售商的资金短缺对其运营策略的影响问题。比如,Goyal[18]在供应商提供延迟支付政策下刻画了零售商的采购策略;Shinn和Hwang[19]进一步讨论了零售商的联合定价及订购策略;占济舟和卢锐[20]分析了资金约束对融资方式的影响问题,他们在市场需求服从均匀分布假设下通过算例分析表明:当零售商自有资金较少时,供应链应采取存货质押的融资方式;而当自有资金大于一定程度时,则应采取商业信用的融资方式。上述文献并不关注资金稀缺的严重程度对订购策略的影响问题。在不考虑破产的情形下,窦亚芹和朱金福[6]探讨了零售商的初始资金量、金融市场的竞争程度和破产成本率对库存策略的影响,研究表明:无论是否对外融资,最优订货量关于初始资金严格递增。杜文意等[21]则在银行融资下分析了初始资金对订购及促销策略的影响:订货量和促销努力水平关于初始资金递增。与上述两篇文献有所不同,陈祥锋[22]在零售商承担有限责任下分析了初始资金对订货策略的影响,得到“订购量关于初始资金递减”的结论。

在上述文献中,窦亚芹和朱金福[6]、杜文意等[21]和陈祥锋[22]与本文最相近,但存在以下区别和联系,首先,这三篇文献分析订货策略关于初始资金的变化关系,而本文讨论订货策略关于资金稀缺度的变化关系。其次,窦亚芹和朱金福[6]及杜文意等[21]在零售商承担无限责任下进行研究,而本文与陈祥锋[22]在有限责任下进行讨论。第三,窦亚芹和朱金福[6]及陈祥锋[22]没有考虑促销问题,而本文与杜文意等[21]则考虑了这一问题,本文研究表明:在零售商促销下,陈祥锋[22]有关“订购量关于初始资金递减”的结论仅在资金稀缺程度较严重的情形下才成立。第四,杜文意等[21]在银行融资下进行讨论,促销资金短缺可通过融资途径予以解决,本文在贸易融资下进行讨论,促销资金短缺不能通过融资途径予以解决。

第三类文献是资金约束供应链的运营优化及契约协调文献,罗春林和骆建文[23]在资金短缺供应商管理库存且零售商促销下刻画了贸易融资和银行融资下的均衡策略,并比较分析了融资模式对广告策略及双方收益的影响。沈建男和邵晓峰[24]则分析了制造商或零售商的销售努力对制造商付款方式的影响问题。上述两篇文献关注供应商(制造商)的资金短缺,与之不同,方磊等[25]研究了资金不足零售商分别通过银行贷款和股权融资时,供应链的最优运营和融资策略以及零售商融资方式的选择问题。本文在零售商资金短缺下探讨契约协调问题,与这一主题相关的文献包括Chod[26]、Yan等[27]以及 Yang 和 Birge[28]。 Lee 和 Rhee[8]在整个供应链面临资金短缺且存在融资成本下分析了回购契约和收益共享契约的协调问题,结果表明:借助商业信用,回购契约能够完成渠道协调,但收益共享契约不能协调供应链。Kouvelis和Zhao[29]在考虑破产成本下的研究表明:如果不存在固定的破产成本,那么收益共享和回购契约都能完成渠道协调;如果存在固定的破产成本,只有收益共享契约能协调供应链。艾兴政等[30]在供应商或零售商提供延保服务下讨论了收益共享契约的协调问题,结果表明:无论哪方提供延保服务,收益共享契约都能协调供应链,且当收益共享比例在一定区间时,成员企业的福利状况都能实现帕累托改进。最近,杜文意等[31]在零售商资金短缺下讨论了供应链的协调问题,他们提出融资成本共担的协调机制,该机制能实现渠道双方成员的期望收益均得到帕累托改善。

在这类文献中,与本文最相近的研究包括鄢仁秀等[32]、鄢仁秀等[33]以及Xiao等[9]。在不考虑促销下,鄢仁秀等[32]、鄢仁秀等[33]分别讨论了回购契约和收益共享契约的协调问题,分析了初始资金对协调契约参数的影响,得到以下结论:在延迟支付下,收益共享和回购契约均能协调供应链,且批发价格随初始资金的增大而减小,而回购价格(在回购契约下)和收益共享比例(在收益共享契约下)随初始资金的增大而增大。上述两篇文献与本文存在以下区别,首先,这两篇文献关注初始资金对契约参数取值的影响,而本文关注资金稀缺度对渠道协调能否实现以及协调契约可行域(参数取值范围)的影响。其次,在这两篇文献提出的协调契约中,批发价格这一参数依赖于随机需求的分布;本文构造的协调契约参数独立于需求分布,具有更好的适用性。第三,在这两篇文献中,要实现渠道协调,延迟支付机制是必须的;本文构造了不需要延迟支付机制的协调契约。Xiao等[9]假定零售商不能直接对外融资,供应商在获得外部贷款后借助贸易信用给零售商融资;本文假定供应商资金充足,使用延迟支付政策向零售商提供贸易信用。Xiao等[9]没有考虑促销问题,研究表明:仅当供应链拥有充足的运营资本时,收益共享和回购契约才能协调供应链;本文在零售商促销下进行讨论,结果表明:无论零售商的资金短缺问题有多么严重,收益共享和促销成本分担机制总能够协调供应链,其中促销成本可在发生时或者期末进行分担。

1 模型及假设

考虑由单一供应商和单一零售商组建的供应链,供应商将某一报童商品卖给零售商,该商品的生产提前期较长且经营期具有季节性,零售商只有一次订货机会,订购量设为q。商品的市场价格、批发价格和单位生产成本分别为p、w和c。商品市场需求是随机的,用非负随机变量ξ来表示,其概率分布函数和密度函数分别为F(ξ)和f(ξ)。为了简化分析,假设F(ξ)严格递增。令(ξ)=1-F(ξ)。

假设1随机变量ξ具有递增的失败率(IFR)。

随机变量ξ的失败率被定义为h(ξ)=f(ξ)(ξ)。 在运营管理领域很多常见的分布函数,如均匀分布、指数分布、正态分布等,都满足这一性质。

供应商实力雄厚、资金充足,但零售商面临资金约束,初始自有资金为A。供应商提供延迟支付政策,如果零售商资金短缺,商品货款可选择延迟支付,延迟支付利率为r。为确保零售商在延迟支付下仍有利可图,约定w(1+r)＜p。

假设2零售商承担有限偿付责任[22,28,29,34]。如果销售收入不足以支付剩余货款和利息,零售商破产,供应商获得全部销售收入作为补偿。

假设3零售商没有其它融资渠道,只能通过供应商提供的延迟支付政策进行贸易融资[9]。

中小企业的融资难是一个普遍现象,由于中小企业难以借助企业信誉获得贷款支持,也不能提供足够的抵押品,难以通过金融机构的融资渠道解决资金短缺问题[35],并且,即使金融机构愿意向零售商融资,只要延迟支付利率r足够低,比如,r等于或略低于金融市场竞争性的贷款利率,零售商也会选择贸易融资[34]。

零售商实施促销努力。特别地,本文讨论的促销是指能直接向消费者推销产品以改善市场需求的一切促销活动,包括销售促进(赠品及优惠券等)、促销广告(不同于通过改善企业形象来间接促进商品销售的品牌广告、观念广告及公益广告等)以及其它旨在直接改善市场需求的销售活动。市场需求的改善程度用e来表示,后文提及为促销强度。在文献中讨论促销对市场需求的影响存在两种广泛采用的模型方法,一是加法模型[36-37],即e+ξ,另一个是乘法模型[38-39],即eξ。在加法需求模型下,即使随机实现的需求为0,仍存在由促销引致的正需求,即但在乘法需求模型下不存在那样的确定性需求。如果存在正的确定性需求,即使随机实现的需求很小,资金短缺的零售商也存在不破产的可能性,但如果没有那样的确定性需求,零售商则始终存在破产风险。资金充足供应链的协调要求零售商不存在破产风险,因此,是否存在促销引致的确定性需求将导致研究结论的显著差异;除此之外,两个需求模型对本文的主要结论没有影响。在现实中,促销对需求的影响介于加法模型和乘法模型之间,即存在促销引致的确定性需求,基于加法需求模型得到的管理洞见比乘法需求模型更具一般性,且与更一般的加法和乘法混合需求模型一致,但加法模型的求解过程及表达形式比混合需求模型更为简洁,基于此,本文采用加法模型。促销费用C(e),它关于e严格凸增,且有C(0)=0及C′(0)＜p-w(1+r),最后一个假设是为了确保零售商的优化问题关于e有严格正的解。

2 资金短缺下零售商的策略分析

给定策略(q,e),在有限偿付责任下,零售商在期末的现金流为

式(1)等式右侧大括号中的第一行表示零售商在期初支付促销费用及商品货款后持有的现金,第二行表示在期末实现的销售收入及需要支付的剩余货款及利息。若A≥wq+C

(e),零售商在期初不存在资金短缺,其优化问题退化为无资金约束下的订购和促销联合决策问题,已有一些文献对此进行了研究[12-13]。本文考虑A＜wq+C(e)的情形。由于贸易融资仅可解决采购资金短缺问题;零售商须使用初始资金支付促销费用,故有C(e)≤A。由C(e)≤A＜wq+C(e),可将(1)简化为:

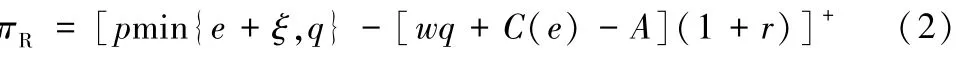
对任意q≥0,恒有[p-w(1+r)]q≥0≥[C(e)-A](1+r),即pq＞[wq+C(e)-A](1+r)。零售商是理性的,其订购和促销策略满足q-e＞0。令

由(2)和(3),有

引理1ξ0＜q-e;除了一个测度为零的空间之外,ξ0关于q和e可微,且ξ0关于q非减,而关于e先减后增,且极小点为。

证明:注意到q-e＞0,若ξ0=0,则ξ0＜q-e;若ξ0＞0,则由pq＞[wq+C(e)-A](1+r)=p(ξ0+e),有ξ0＜q-e。 综上,ξ0＜qe。利用ξ0的定义容易表明ξ0关于q和e连续,且当ξ0＞0时,ξ0关于q和e可微。令,并用N°表示N的内部,即ξ0=0的内点集合,则对任意(q,e)∈N°,ξ0关于q和e可微。

令ς=(wq+C(e)-A)(1+r)-pe。ς关于q严格增且关于e严格凸,其极小点为^e,因而对任意给定的e,存在唯一的q(e)使得ς=0;而对任意给定的q,至多存在两个点e1(q)和e2(q),使得ς=0。

既然ξ0=(ς)+/p,因此,除了一个测度为零的空间,ξ0关于q和e可微,且对∀,有∂ξ0/∂e≤0。 证毕。

2.1 零售商的最优策略

零售商面临的问题是:确定q和e以最大化期末现金流的数学期望E[πR],即(P1)

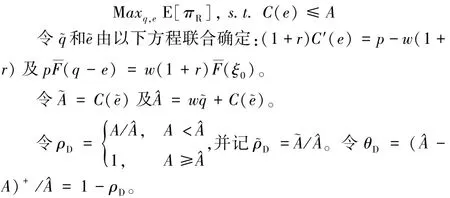
ρD∈(0,1]和θD∈[0,1)分别度量了资金充裕及稀缺状况,为了阐述的方便,后文分别提及为资金充裕及稀缺系数。ρD(θD)取值越小(大),零售商的资金稀缺程度越严重。特别地,用下标D指代分散决策,以与集中决策下的对应指标相区别。若ρD=1(θD=0),零售商资金充足,相关讨论退化为无资金约束情形。除非特别说明,后文总是假定ρD＜1。使用这两个指标中的任何一个进行分析所得结论完全一致,为了讨论的方便,后文使用ρD。

下面分两种情形讨论。第一种情形:≤ρD＜1。在这种情形下,问题P1的约束不起作用。

命题1若≤ρD＜1,E[πR]是关于q和e的联合拟凹函数,零售商的最优策略(q*,e*)由以下两式联合刻画:

证明:令 ∂E[πR]/∂q=0 及 ∂E[πR]/∂e=0, 可 得(5)和(6)。

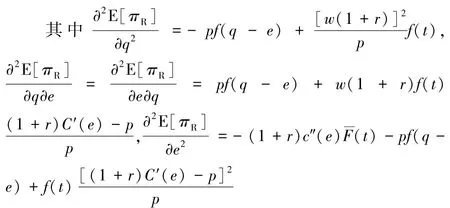
要证E[πR]关于q和e联合(严格)拟凹,只需表明矩阵H在满足(5)和(6)的点是(严格)负定阵。由(5)和(6),有及(1+r)C′(e)-p=-w(1+r),因而有

利用上面三个式子,可得

这就完成了证明。

在贸易融资下单位资金的使用成本为1+r。当促销强度为e时,继续增大促销力度的边际成本为(1+r)C′(e),为满足促销引致的额外市场需求,需增加订货量,其单位采购成本为w(1+r),商品的边际收益为p,边际收益等于边际成本给出式(6)。商品采购的边际成本为w(1+r),这个成本仅当零售商不破产时才会承担,发生的概率为;商品若实现销售可得收入p,实现销售的概率为,这就给出了式(5)。

第二种情形:0＜ρD≤ρ~D。在这种情形上,问题P1的约束绷紧,即C(e*)=A。对任意给定的e,E[πR]关于q严格凹,利用E[πR]关于q的一阶最优条件,可得以下结论。

命题2若0＜ρD≤ρ~D,零售商的最优策略(q*,e*)由以下式子联合确定:

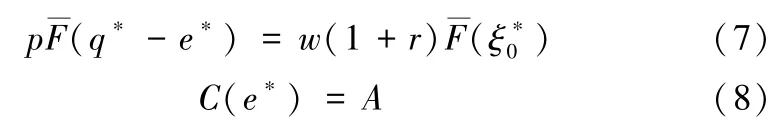
由于促销成本需事先支付,当ρD≤时,零售商没有足够的资金来实施最优促销策略e~。因p＞(1+r)C′(e)+w(1+r),促销的边际收益大于边际成本,零售商有激励将所有初始资金用于促销,所有商品货款通过延迟支付方式解决。

2.2 资金稀缺度对最优策略的影响分析

定理1在区间(0,1),q*和e*关于ρD连续,且e*关于ρD递增,而q*关于ρD递减。特别地,有:(1)若D＜1,e*独立于ρD的变化,而q*是ρD的减函数,当且仅当＞0时,q*关于ρD严格递减。(2)若0＜ρD＜,e*关于ρD严格递增,q*关于ρD严格递减。

证明:当ρD=ρ~D,即时,由命题1和命题2确定的q*和e*相等,即q*和e*关于ρD连续。

下面仅对第(2)部分进行证明,第(1)部分的证明类似,略去。

(2)由(8),有 ∂e*/∂A=1/C′(e*)＞0。 对(7)两侧求关于A的偏导数,得到

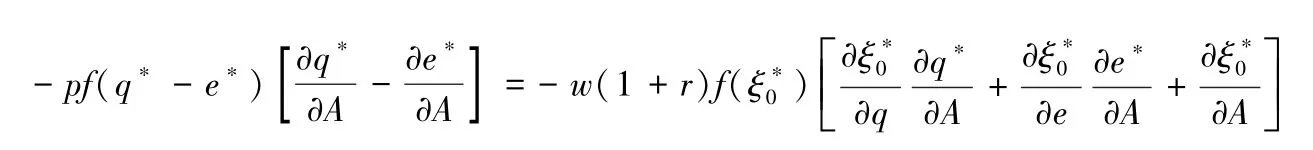
将上式变形后,得到

利用式(7),可将上式化简为

如果0,则除了一个测度为零的空间,有/∂q=/∂e=/∂A=0,利用这个事实,可将(9) 简化为-∂q*/∂A=∂e*/∂A。 由∂e*/∂A＞0,可得 ∂q*/∂A＜0。 如果0,(9)可简化为

利用上式,并注意到 ∂e*/∂A＞0,可得 ∂q*/∂A＜0。

根据ρD的定义并注意到是严格正的常数,则∂e*/∂ρD与 ∂e*/∂A,∂q*/∂ρD与 ∂q*/∂A有完全相同的正负号。 证毕

直觉上,随着ρD增大(等价地,θD减小),零售商拥有更大的支付能力来采购商品并开展促销活动,即q*和e*关于ρD递增(关于θD递减)。 但在延迟支付政策下,资金短缺的零售商可选择贸易融资缓解资金周转困难,其运营策略并不受限于自有资金的支付能力。

由于采购资金短缺可通过延迟支付予以解决,零售商将把初始资金优先用于促销活动。ρD越大,促销策略的选择空间越大,促销强度随ρD严格递增,直至最优策略e~得以实施。此后,随着ρD的进一步增大,零售商不再投入更多的资金用于促销,这是因为促销的边际收益不变而边际成本递增,当~时,促销的边际收益小于边际成本。

θD越大,资金短缺问题越严重,同样策略下破产的可能性越大,零售商实际承担责任的概率越小,因而越有激励采取冒险策略,即采购更多的商品;反过来,ρD越大,破产可能性越小,零售商愈发关注期望利润的大小,经营行为越谨慎。

当D＜1时,初始资金足以支付最优促销费用,e*独立于ρD的变化。若0,初始资金的微小变化不改变与零售商破产相对应的市场需求的临界值,故对采购策略没有影响。当0＜ρD时,e*~,e*关于ρD严格递增,在这种情形下,即使0,q*也会随ρD的变化而变化:资金稀缺度越严重,零售商的订购量越大,促销强度越弱。

引理2存在唯一的∈(0,1),当且仅当ρD≥时,有0,且q*=e*(w(1+r)/p)。

证明:首先证明:存在唯一的∈(0,),当且仅当A≥时,有=0。

为了强调关于A的依赖性,记(A)。根据的定义,有＞0。

当A=0时,有ρD,因此,q*和e*由(7)和(8)联合确定,显然有e*=0且q*＞0,由(3)可得(0)＞0。当时,有ρD,q*和e*由(5)和(6)联合确定,显然有e*~＞0且q*~。根据的定义,有wq*+C(e*)~+C(~),因此,()=0。

(A)关于A在区间和(]连续是显然的。由定理1,(A)在点也连续,因而(A)在区间[0,]连续。

令ς(A)=(wq*+C(e*)-A)(1+r)-pe*,则有(A)=[ς(A)]+/p。 很显然,ς(A) 在区间[0,]连续,且ς()＜0。由定理1,q*和e*在区间(0,)关于A连续,因而存在一个充分小的正数δ,使得ς()＜0,故有()=0。 由引理1和定理1,(A)关于A在区间和()递减。因此,存在A′∈(0,)满足以下条件:当A≥A′时,有(A)=0。

推论1当且仅当ρD∈(max{},1)时,q*和e*均独立于ρD的变化。

证明:直接由引理2和定理1可推得结论。

是资金充足和短缺的临界点。当资金充裕(ρD=1)时,q*和e*独立于ρD的变化是易于理解的,因为支付货款和促销费用后存在剩余资金,初始资金的微小改变对零售商的策略无影响。根据推论1,只要资金稀缺度不严重,资金量的微小改变就不会影响零售商的策略,这与资金短缺严重的情形不同:当资金极其短缺时,q*和e*中至少有一个会随着ρD的变化而变化(定理1)。 定理1和推论1的结果总结在表1中。

表1 ρD对q*和e*的影响Table 1 Im pact ofρon q*and e*D

在零售商承担无限责任下,杜文意等[21]研究表明:订货量和促销努力水平关于初始资金递增,这与定理1不一致,造成这种差异的原因在于零售商承担的偿还责任不同。在有限责任下,陈祥锋[22]在不考虑促销下的研究表明:零售商的订购量关于初始资金递减。根据表1,在零售商促销下,陈祥峰[22]的结论在ρD＜ρ~D下成立,在ρ~D＜1下有限地成立。max{,}是一个临界值,当且仅当ρD大于这个临界值时,订货量独立于A的变化。

3 供应链的协调

作为比较的标准,首先给出集中决策下供应链的最优策略。供应商的资金充足,整个供应链不存在资金约束问题。给定(q,e),供应链的利润为:ΠSC=pmin{e+ξ,q}-cq-C(e)。供应链的期望利润E[ΠSC]关于q和e(严格地)联合凹,使用一阶最优条件方法可得集中决策下最优生产量qI*和促销强度eI*:

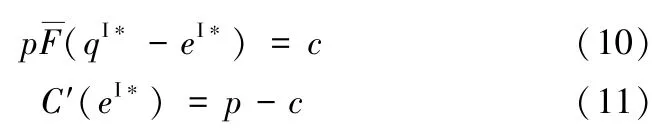
由(11)及成本函数的严格凸性,有C(eI*)＜(pc)eI*。用表示最优策略下供应链的利润。由(10)和(11),有(qI*,eI*)≠(0,0),由E[ΠSC]的严格凹性,必有E[]＞ 0。

令AI*=cqI*+C(eI*),它表示在集中决策的最优策略下商品采购与促销的成本之和,是在集中决策下实施最优策略要求的最低资金量。

若ρI=1,零售商使用初始资金可实施集中决策的最优策略,供应链的协调总可实现[12,13]。除非特别说明,后文总是假定ρI＜1。4.4小节将简单讨论ρI=1的情形。

令(eI*)/AI*,表示在集中决策的最优策略下促销成本占总成本的比例。在批发价格契约下,若ρI,则由定理1,有e*＜eI*,因而渠道协调不可实现。即使ρI＞,比较(5)和(10),有w(1+r)()=c;由(6)和(11),又有(1+r)C′(e*)=p-w(1+r) ≤p-c=C′(eI*),故有C′(e*)＜C′(eI*),即e*＜eI*。综上,批发价格契约不能协调供应链(唯一的例外是ρI,即A=C(eI*),但这种情形的概率测度为零)。

下面考虑收益共享与促销成本分担契约,记为(w,φ,α),契约规定如下:商品批发价格为w;双方共同分享销售收入,零售商和供应商的分享比例分别为φ和1-φ;双方共同承担促销成本,两者分担比例分别为α和1-α(在现实中的具体表现形式为供应商向零售商支付场地使用费及促销费等)。为了避免平凡的讨论,约定φ∈(0,1)且α∈(0,1)。

供应商和零售商之间还可能存在固定的单边转移支付(lump sum side payment)T,其取值可正可负(在现实中表现为供应商向零售商支付的渠道管理费,或零售商向供应商支付加盟费等)。由于T只影响最终的利润分配,并不影响双方的最优决策,后文将忽略这一变量。第3小节假定供需双方可通过调整T来确保双方的参与约束得到满足,第4小节考虑不允许单边转移支付的情形。

博弈过程如下,在销售期初,零售商促销并用初始资金支付促销费用,供应商分担部分促销成本(促销成本的结算可在销售期初或期末进行);供应商按零售商的订货要求提供数量为q的商品并在期初交付,如果零售商资金短缺,可以选择延迟支付货款,延迟支付的利率为r;销售收入实现后,双方共同分享,零售商用销售收入支付未付货款及利息。零售商承担有限责任,如果销售收入不足以支付货款,剩余货款不再支付。

由于销售收入的不确定性,收益共享只能在季末(销售收入实现后)进行;与之不同,促销成本在期初发生且数量确定,易于证实,在销售期初分摊这一成本具有现实基础。基于此,下面分别考虑促销成本在期初和期末进行分摊两种情形下的契约协调问题。为了行文方便,将促销成本在期初和期末进行结算分别提及为及时结算(instant settlement)和延后结算(delayed settlement);后文中用上标is和ds分别指代这两种情形。

3.1 促销成本延后结算

如果延后结算促销成本,在契约(w,φ,α)下,零售商在期末的现金流为:

促销费用事先支付要求A≥C(e),基于此,式(12)可简化为:

在收益共享契约下,w小于c,因此,A＜AI*不能排除A≥wq+C(e)这种可能性。

(1)若wq+C(e)≤A,则最优策略(qds*,eds*)满足以下两个一阶最优条件:

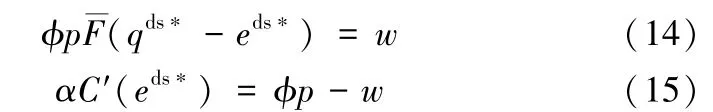
(2)若wq+C(e)＞A,则最优策略(qds*,eds*)满足:

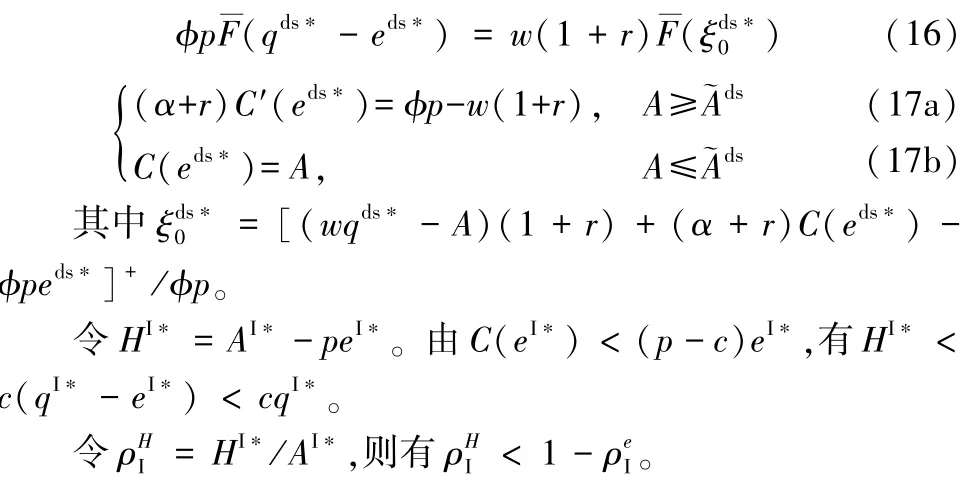
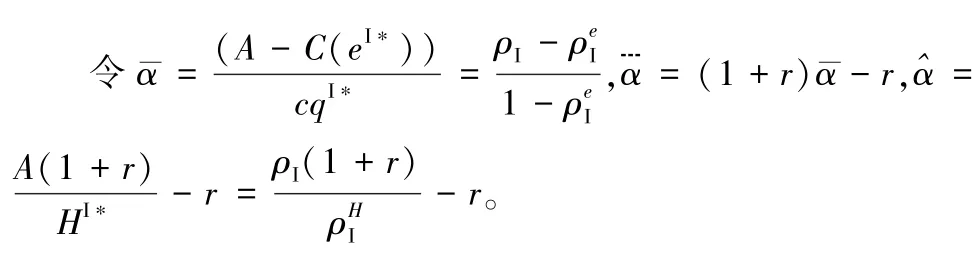
定理2在延后结算促销成本下,(1)当ρI＜1时,契约(w,φ,α)可以协调供应链,其中协调契约参数满足:

在对定理2证明之前,先给出一个技术性引理。

令ξA=[(α+r)[cx+C(eI*)-peI*]-A(1+r)]+,ξB=[α[cx+C(eI*)-peI*]-A]+。

考虑如下关于x的方程:

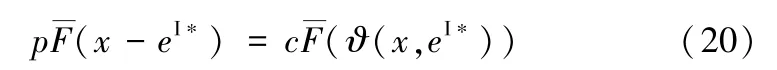
引理3(1)若α＜α^,则当ϑ(x,eI*)=ξds/(α+r)p时,方程(20)存在唯一解qI*。(2)若α＜,则当ϑ(x,eI*)=ξis/αp时,方程(20)存在唯一解qI*。

引理3的证明:(1)如果α＜,那么ϑ(qI*,eI*)=0,由(10)可知qI*是方程(20)的解。

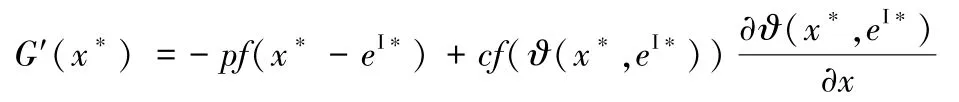
若ϑ(x*,eI*) ＞ 0,则G′(x*)(x*-eI*)[-pz(x*-eI*)+cz(ϑ(x*,eI*))]＜0,最后一个不等号来自假设1。

若x*∈M°,则有G′(x*)=-pf(x*-eI*) ＜ 0;若x*∈M′,G(x)在点x*的导数不存在,其左导数G-′(x*) 和右导数G′+(x*) 分别为:G′-(x*)=-pf(x*-eI*);G′+(x*)=F(x*-eI*)[-pz(x*-eI*)+cz(ϑ(x*,eI*))]＜0。综上,则对方程(20)的任意解x*,G(x)在x*处严格递减,因此,仅有唯一的x*满足G(x*)=0。

(2)与第(1)部分的证明相同,略。

定理2的证明:只对第(2)部分进行证明。

由r＜1,有max{ρeI,rρHI/(1+r)}＜ρeI+(1-ρeI)/(1+r),故存在ρI∈ (max{ρeI,rρHI/(1+r)},ρeI+(1-ρeI)/(1+r))。

注意到max{ρeI,rρHI/(1+r)}＜ρI＜ρeI+(1-ρeI)/(1+r)与max{C(eI*),rHI*/(1+r)}＜A＜C(eI*)+cqI*/(1+r)等价。由r＜1,可得rHI*/(1+r)}＜C(eI*)+cqI*/(1+r),故存在A∈ (max{C(eI*),rHI*/(1+r)},C(eI*)+cqI*/(1+r))。下证(19)定义的契约非空,即要表明。

将(19)代入(17a),有C′(eds*)=p-c=C′(eI*),既然C(·)严格增,故eds*=eI*,将其及(19)代入(16),可得

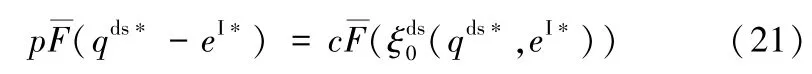
既然α＜,则必有(1+r)-r,由(21)和引理3,有qds*=qI*。

最后,由α＞,有:

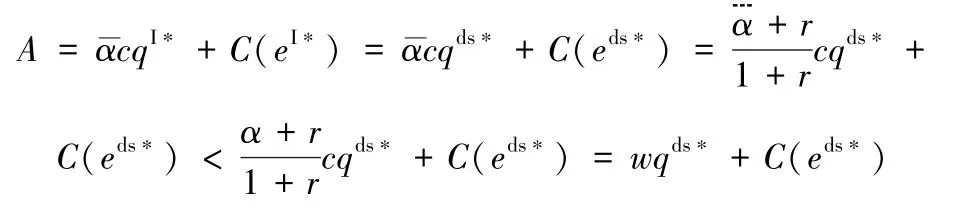
既然A＞C(eI*),因此,在(19)定义的契约下,(qds*,eds*)是由(16)和(17a)联合确定的。定理2得证。

定理2刻画了延后结算促销成本下协调契约(w,φ,α)的参数满足的条件,分别由(18)和(19)刻画。在(18)定义的契约下,零售商在期初不存在资金短缺,不会选择延迟支付,协调契约参数之间的关系与无资金约束情形相同,但协调契约的可行域(由α的取值空间来表示)比无资金约束的情形要小((0,)⊂(0,1))。 若ρI=1,则1。 在(19)定义的契约下,初始资金不足以支付商品货款和促销成本,部分货款选择延迟支付。作为补偿,零售商在期末分享更高比例的销售收入,以实现供应链的协调。根据定理2,如果促销成本延后结算,要使用契约(w,φ,α)协调供应链,当且仅当ρI＞。若资金短缺严重,即ρI＜ρeI,供应链的协调不可实现,其根源在于零售商没有足够的初始资金支付促销费用,A＜C(eI*),最终实施的促销强度小于渠道协调要求的促销强度。

3.2 促销成本及时结算

如果及时结算促销成本,在契约(w,φ,α)下,零售商在期末的现金流为:

在及时结算下,零售商在期初只需承担α部分的促销费用,故有A≥αC(e)。利用这一结果,可将(22)简化如下:

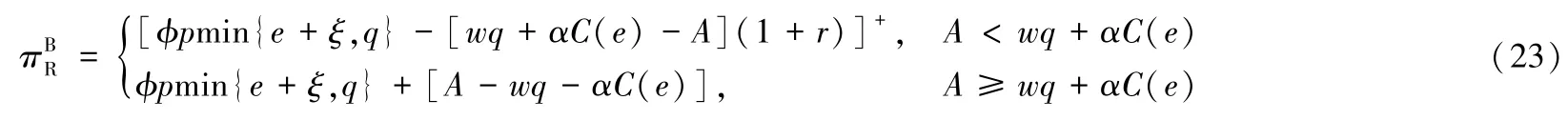
(2)如果wq+αC(e)＞A,最优策略(qis*,eis*)则由以下两式隐含确定:

定理3在及时结算下,(1)当ρI＜1时,契约(w,φ,α)可以协调供应链,其中协调契约参数满足:

(2)当ρI＜1/(1+r) 时,契约(w,φ,α)可以协调供应链,其中契约参数满足:

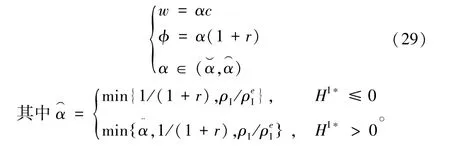
(3)当ρI≤时,如果cqI*≤peI*,契约(w,φ,α)可以协调供应链,其中契约参数满足:

证明:(1)由ρI＜1,有 0＜＜1,(28)定义的契约非空。将(28)置入(24)和(25),有(qis*,eis*)=(qI*,eI*)。

下面确认:在(28)定义的契约下,(qis*,eis*)由(24)和(25)联合确定。由α∈(0,],有

因此,(qis*,eis*)由(24)和(25)联合确定。

(2)注意到φ∈(0,1)及φ=α(1+r),要确保(29)定义的契约参数有意义,要求α＜1/(1+r),否则φ≥1。

ρI＜ρI及ρI＜是显然的,注意到ρI＜1/(1+r),显然有=ρI＜。 因此,(17)定义的契约参数空间非空。

将(29)代入(27a),有C′(eis*)=p-c=C′(eI*),既然C(·)是严格增函数,因此,有eis*=eI*。 把这一结果代入(26),并利用(29),可得

最后,需要确认在(29)定义的契约下,(qis*,eis*)由(26)和(27a)联合确定。

(3)与前两部分的证明类似,略去。证毕。

定理3刻画了及时结算促销成本下协调契约(w,φ,α)的参数需满足的条件。第一种情形由(28)刻画,在这种情形下,通过收益共享(零售商的采购成本小于供应商的生产成本)和促销成本分担机制,可确保零售商在销售期初资金充足。协调契约参数之间的关系与无资金约束情形相同,但可行域比无资金约束情形要小((0,]⊂(0,1))。

第二种情形由(29)刻画,零售商在期初需承担较大的商品采购和促销成本(促销成本分担比例更大,批发价格更高),以至于运营资金不足,故将延迟支付部分货款。为了完成渠道协调,相对于无资金约束情形,参数之间的关系需要修正为φ=α(1+r)(在无资金约束下有φ=α),这是因为:在延迟支付下,零售商的边际采购成本为w(1+r)而非w。通过参数设计,可确保零售商的初始资金足以支付(分担的)促销成本,且有部分剩余资金用于支付商品货款。

第三种情形由(30)刻画,零售商承担的促销成本比例比前两种情形更高。若资金短缺极其严重,可让零售商在期初仅承担部分促销成本且延迟支付所有商品货款。通过选择契约参数α=,可确保零售商使用初始资金实施集中决策下的最优促销策略。据此,要协调供应链,只需设定契约参数w和φ来确保零售商的订货量与集中决策一致。由于延迟支付下的边际采购成本为w(1+r),在收益共享契约下,要协调订货量要求契约参数满足w(1+r)=φc。

一般地,仅仅通过收益共享或者促销成本分担机制不能实现对供应链的协调。通过促销成本分担机制,可诱导零售商选择供应链最优促销策略[13];通过收益共享机制,则可诱导零售商选择集中决策下的最优采购策略[13]。关于零售商的资金短缺问题,存在两种协调机制,第一种,使用延迟支付机制,供应商为零售商融通资金;第二种,联合使用收益共享和促销成本分担机制,通过减小批发价格并分担零售商的促销成本,将商品货款和促销成本控制在初始资金支付能力之内。从前面的讨论可知,收益共享和促销成本分担(及时结算)机制在本质上具有融资功能。总之,延迟支付机制并不是解决零售商资金短缺问题的唯一选项——这一结论也可拓展到其它融资途径。

如果促销成本延后结算,零售商在期初至少需要支付全部促销费用。要实现供应链的协调,必然要求初始资金大于集中决策下的最优促销费用,这一限定在促销成本及时结算下是不存在的。因此,从渠道协调这一视角来看,及时结算促销成本进一步减少了对初始资金的要求。

3.3 资金稀缺度对供应链协调的影响分析

表2对定理2和定理3的结果进行了总结。根据零售商资金稀缺情况,有五种协调契约可供选择,为方便阐述,用符号Ⅰ-Ⅴ对协调契约进行区分,见表2最后一栏。

表2 协调契约参数满足的条件Table 2 Conditions satisfied by the parameters of coordination contracts

根据促销成本的结算时间以及是否包括延迟支付机制两个维度,可将上述五种契约进行归类,如表3所示,其中契约Ⅰ和Ⅳ不使用延迟支付机制(即使供应商提供这一政策,零售商也不会选择贸易融资),契约Ⅱ、Ⅲ和Ⅴ则包含延迟支付机制。

表3 契约分类Table 3 Contract classification

给定资金稀缺度,在契约Ⅰ-Ⅴ里可能存在多个契约可完成渠道协调,见表4。

在及时结算促销成本下,随着资金稀缺度的下降,能协调供应链的契约种类随之减少,隐藏在背后的逻辑如下:无论资金稀缺度如何,总可设计那样的契约机制,以至于零售商在期初不存在资金短缺问题;但随着资金稀缺度的下降,要设计能诱导零售商选择延迟支付的协调契约更困难,因为那样的契约要求零售商在期初分担更高的促销成本比例,而这一比例是有上界的。比如,在(29)中,成本分担比例的上界为,而要诱导零售商选择延迟支付,要求α＞⌒α,若⌒α≥,(29)定义的契约可行域是空集。在延后结算促销成本下,上述有关“随着资金稀缺度的下降,协调契约的种类随之减少”的结论并不成立,见表4的第b)部分。

表4 在不同的资金稀缺度下供应链的协调契约Table 4 Coordination contracts under different degrees of shortage of fund a)r2/(1+r)≤≤1-

表4 在不同的资金稀缺度下供应链的协调契约Table 4 Coordination contracts under different degrees of shortage of fund a)r2/(1+r)≤≤1-

资缺金程稀度 0 ＜ ρI≤ρe IρI＜ 1/(1+r) 1/(1+r)≤ ρI＜ ρ ρe I e I +＜( 1ρI- ＜ ρ e I 1)/(1+r) ρe I+(1- ρe I)/(1+r)≤ ρI契约类型 Ⅰ、Ⅱ、Ⅲ Ⅰ、Ⅱ、Ⅳ、Ⅴ Ⅰ、Ⅳ、Ⅴ Ⅰ、Ⅳb)rρe I＜r2ρH I/(1+r)＜1-ρe I资金稀 ρe I ＜ ρI＜ 1缺程度 0 ＜ ρI≤ ρe IρI ≤ rρH I/(1+r) rρH I/(1+r) ＜ρI＜ 1/(1+r) ρe I1+/((11+-r)ρe I≤)/(ρ1I+＜r) ρe I+(1- ρe I)/(1+r) ≤ ρI契约类型 Ⅰ、Ⅱ、Ⅲ Ⅰ、Ⅱ、Ⅳ Ⅰ、Ⅱ、Ⅳ、Ⅴ Ⅰ、Ⅳ、Ⅴ Ⅰ、Ⅳc)1-ρe I≤rρe I资金稀0 ＜ ρI≤ ρe Iρe I ＜ ρI＜ 1缺程度 ρI＜1/(1+r) ρI＞1/(1+r) ρI＜ρe I+(1-ρe I)/(1+r) ρI＞ρe I+(1-ρe I)/(1+r)契约类型 Ⅰ、Ⅱ、Ⅲ Ⅰ、Ⅲ Ⅰ、Ⅳ、Ⅴ Ⅰ、Ⅳ

推论2对任意ρI∈(0,1),契约Ⅰ总能协调供应链。

证明:直接由定理2可推得结论。

尽管资金稀缺度影响协调契约的选择,但无论稀缺程度如何,契约Ⅰ总是有效的。特别地,即使ρI=1,契约Ⅰ仍能协调供应链。总之,若供应商资金充足而零售商资金短缺,渠道协调总可以实现。在不考虑促销下,Xiao等[9]研究表明:仅当供应链拥有充足的运营资金时,收益共享契约才能协调供应链,这与推论2的结论在本质上是一致的。

3.4 进一步讨论

推论3(1)在契约Ⅱ、Ⅲ和Ⅴ下,有在契约Ⅰ-Ⅴ下,对任意ξ＞0,有

证明:(1)直接由定理2和定理3可推得相关结论。

(2)在契约Ⅰ和Ⅳ下,有A＞wqI*-αC(eI*),与(13)和(23)相结合,可得在契约Ⅱ、Ⅲ和Ⅴ下,有因而对任意ξ＞0,有及证毕。

在契约Ⅰ和Ⅳ下,通过减小批发价格并分担促销成本,将零售商在期初的支付总额控制在支付能力之内,零售商不融资,不存在破产的可能。在契约Ⅱ、Ⅲ和Ⅴ下,尽管选择贸易融资,但由于存在确定性的销售收入peI*,只要零售商分享的销售收入大于融资金额及利息,零售商就不会破产。比如,在契约Ⅲ下,有w(1+r)qI*=φcqI*≤φpeI*,零售商不会破产。

推论3揭示了以下管理启示:要实现对供应链的协调,可以设计那样的风险分担机制,以至于无论市场需求的随机实现如何,零售商都不会破产。当然,零售商仍有可能出现亏损,即

在乘法需求模型eξ下,如果及时结算促销费用,则有注意到由(29)刻画的契约对应着wqis*+αC(eis*)＞A,由(30)刻画的契约对应着αC(eis*)=A,在这两种情形下,恒有0,即零售商存在破产风险,但供应链协调要求即不存在破产风险,因此,契约Ⅱ和Ⅲ将不能协调供应链。类似地,在延后结算下,有,在这种情形下,通过限定α的取值范围(φ和w的取值范围随之确定),可确保供应链的协调仍可以实现,即契约Ⅴ可以协调供应链,但参数的取值范围需要进行修正。

在契约Ⅰ和Ⅳ下,零售商不对外融资,因而不存在破产的可能。无论是采用乘法需求模型还是加法需求模型,对所得结论(包括协调契约参数之间的关系及取值范围)均没有影响。

前文在ρI＜1下进行讨论。事实上,定理2和定理3可自然地拓展到ρI=1的情形。

推论4如果ρI=1,在上述五种契约中,只有契约Ⅰ和Ⅳ能够协调供应链,且契约Ⅰ和Ⅳ的参数关系及取值空间完全相同,即w=φc=αc∈(0,c)。

在资金充足下,促销成本是及时结算还是延后结算对协调供应链是无关紧要的,这与直觉相符。在资金充足下,零售商不会使用贸易信用,契约Ⅰ和Ⅳ在本质上是同一个契约。但在资金短缺下,促销成本的结算时机至关重要。

根据推论4及前面的讨论,若ρI=1,采用加法需求模型或者乘法需求模型所得结论完全一致。若资金充足,无论市场需求的随机实现如何,零售商都不会破产。在这种情形下,是否存在由促销引致的确定性需求对契约协调没有影响。

前文对供应链协调的讨论没有考虑成员企业的参与约束。若契约(w,φ,α)能诱导分散决策下零售商的策略与集中决策下的最优策略一致,借助单边转移支付机制,总可确保供应商和零售商都参与供应链,从而实现对供应链的协调。但如果不允许单边转移支付[39],上述契约还能协调供应链吗?接下来讨论这一问题。

4 不允许单边转移支付

分别用ΠR和ΠS表示零售商和供应商的利润,在促销成本延后或及时结算下,有表示策略(qI*,eI*)下的ΠR。令假设零售商和供应商的保留效用均为零。在不允许单边转移支付下,要确保成员企业均参与供应链,必然要求0＜k＜1。

4.1 协调契约

引理4ρ1＜1且ρ2＜1,且有以下结论:(1)若HI*≤0,则当r＜r′时,有ρ1＜ρ2,其中r′满足若HI*＞0,则当r＜min{r′,r″} 时,有ρ＜ρ,其中r″12满足

证明:ρ1＜1及ρ2＜1是显然的。 注意到ρ2关于r严格递减可完成其它部分的证明。证毕。

根据r′和r″的定义,有:r′＜1 且r″＜1。

定理4如果不允许单边转移支付,则有以下结论:(1)契约Ⅰ和Ⅳ仍然有效。

(2)当ρI≤时,若cqI*≤peI*,则契约Ⅲ有效,但参数间的关系需要修正为及α=。

(4)当ρI∈ (ρ1,ρ2) 时,若r＜ min{r′,r‴},则契约 Ⅴ 有效,契约参数须满足其中

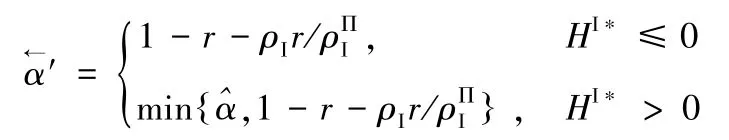
证明:只对第(3)部分进行证明,其它部分的证明类似。

很显然,对任意α＞0,有k＞0。而k＜1必然要求

关于协调条件,契约Ⅰ、Ⅱ和Ⅳ只对资金稀缺度进行了限定,因而总存在那样的供应链。契约Ⅲ的有效性依赖于cqI*≤peI*这一假设,即商品生产成本小于因促销引致的确定性销售收入。如果商品属于奢侈品,对促销很敏感,相对于生产成本,商品售价极其高昂,那么上述假设可能成立。契约Ⅴ的成立要求r＜min{r′,r‴},只要r足够小,这一条件总能得到满足。

4.2 单边转移支付对契约协调的影响分析

定理4将定理2和定理3的结论拓展到不允许单边转移支付的情形。在允许或不允许单边转移支付两种情形下,契约Ⅰ和契约Ⅳ均有效,且契约参数之间的关系及取值范围在两种情形下完全相同。但契约Ⅱ、Ⅲ、Ⅴ在两种情形下存在明显差异,首先,可被协调的供应链的范围减小,比如契约Ⅱ在有无单边转移支付下分别要求ρI＜1/(1+r)及ρI＜min{1/(1+r),/r}。 其次,契约的柔性减弱,其中柔性可用k的取值范围(等价地,协调契约自由参数的取值空间)来度量,如表5所示。

表5 五种契约在有无单边转移支付机制下的比较分析Table 5 Com parison of five contracts in the presence of lum p side payment w ith ones in the absence of side transfer payment

在契约Ⅰ和Ⅳ下,由于k=α且,因此,无论是否允许单边转移支付,均有0＜k＜1。在契约Ⅱ、Ⅲ和Ⅴ下,零售商选择延迟支付货款,ρI不仅影响协调契约参数的取值空间,也直接作用于利益分配比例k,这是因为资金稀缺度影响延迟支付金额及利息。要确保双方均参与渠道协作,即k∈(0,1),要求对自由参数α(φ)的取值范围进行限定,从而要求对α(φ)的上下确界进行修正,这又反过来作用于ρ1的取值范围,以确保α(φ)的取值范围非空。因此,不允许单边转移支付减小了供应链被契约Ⅱ、Ⅲ或Ⅴ协调的可能性。

4.3 资金稀缺度对契约可行域及利益分配的影响

引理5关于ρI严格递增关于ρI递增。

推论5契约Ⅰ和Ⅳ的参数取值空间关于ρI严格递增。

如果不借助延迟支付(见表3),契约(w,φ,α)虽能协调供应链,但在资金短缺下渠道收益的任意分配不可实现,且资金稀缺度越严重,契约可行域越小,渠道收益的柔性分配受到更大的限制。k的取值范围由契约自由参数的可行域确定。用和分别表示k取值的上确界和下确界,利用引理5可得以下结论。

推论6和均是关于ρI的增函数。

若不允许单边转移支付,在渠道协调下零售商分享的最低利润及最高利润随ρI递增。资金稀缺度限定了利益分成的谈判范围,因而在一定程度上反映了零售商的议价能力。由推论6,零售商的资金稀缺度越严重,议价能力越小。

5 结束语

资金短缺影响零售商的策略选择,并对渠道协调施加重要影响。本文在“零售商促销且融资途径仅限贸易融资(延迟支付)”下探讨零售商的运营策略及供应链的协调问题。由于延迟支付只能解决采购资金短缺问题,不能解决促销资金短缺问题,在零售商促销下,供应链的协调面临更大的挑战。

本文构造了一个相对指标来衡量资金的稀缺程度,并运用这个指标分析了资金稀缺度对运营策略的影响,结果表明,存在一个临界值,当资金稀缺度大于这个临界值时,订货量关于资金稀缺度递增,促销强度关于资金稀缺度递减;当资金稀缺度小于这个临界值(资金仍然短缺但不太严重)时,订货及促销策略不随资金稀缺度的变化而变化。

本文设计了五种收益共享与促销成本分担的协调机制,根据零售商资金的稀缺程度,可从五种协调契约中选择一种或多种契约来协调供应链。研究得到以下结论,第一,若延后结算促销成本,仅当初始资金大于集中决策对应的最优促销费用时,供应链的协调才可实现;若及时结算促销成本,则不管资金稀缺度如何,始终存在契约机制能协调供应链。第二,如果不需要诱导零售商选择延迟支付来协调供应链,单边转移支付是不必要的;否则,允许单边转移支付将增大供应链被协调的可能性,且使得利益分配更有柔性。第三,零售商的资金稀缺度越严重,议价能力越小;且在不使用延迟支付机制下,协调供应链的契约可行域随之减小,但协调契约的种类随之增多。

研究揭示了以下管理启示,首先,要协调零售商资金短缺的供应链,延迟支付机制并非必不可少。针对资金短缺问题,存在两种协调机制,一是延迟支付机制,通过融资解决资金短缺问题;二是收益共享和促销成本共担机制,通过减小批发价格并分担促销成本,将零售商在期初的支付总额控制在初始资金的支付能力之内。其次,在资金充足下,促销成本的分摊时机对协调供应链无关紧要,但在资金短缺下却至关重要:及时结算促销成本比延后结算更有效。第三,收益共享和促销成本分担(及时结算)机制在本质上具有为零售商融资的功能;而单边转移支付机制在一定程度上具有渠道协调功能。最后,要实现对供应链的协调,可以设计那样的风险分担机制,使得零售商在期末获得的销售收入大于延迟支付金额及利息,如此,无论市场需求如何,零售商都无破产风险。

本文的讨论基于加法需求模型,相关结论可以自然地拓展到加法和乘法混合需求模型。在乘法需求模型下,由于不存在促销引致的确定性需求,契约Ⅱ和Ⅲ不能协调供应链,契约Ⅰ、Ⅳ(需要修正)和Ⅴ仍然有效。特别地,仅当零售商资金短缺时,在两个需求模型下所得结论才存在差异,若零售商资金充足,需求模型的选择对研究结论没有影响。