圆形扩展风机基础温度场和温度应力仿真分析

刘明华，杜志达，任金明，郭 晨，理倞哲

(1.中国电建集团华东勘测设计研究院有限公司， 浙江 杭州 311122；2.大连理工大学 建设工程学部， 辽宁 大连 116024)

随着“十四五”规划的提出，我国第三大发电方式的风力发电未来仍将是发展的重点，具有广阔的市场[1-2]。陆上建设的风电机组基础形式包含有板式独立扩展基础、桩基础和岩石锚杆基础等，目前圆形扩展基础仍是主要的应用类型[3]。圆形扩展基础一般使用500 m3左右的混凝土，结构实体最小几何尺寸不小于1 m，属于大体积混凝土结构[4]。由于风机基础混凝土在浇筑过程中产生大量的水化热，且混凝土内外散热不均匀，易产生温度裂缝[5]。如李子箐风电场最早浇筑的11基基础混凝土中有8基产生了温度裂缝[6]；东海某风电场项目7号和8号机组基础承台及台柱混凝土浇筑完成后，均出现不同程度的裂缝[7]。温度应力是风机基础产生各类裂缝的重要原因，而混凝土裂缝会破坏结构整体性，降低构件的刚度，影响结构的承载能力，为侵蚀性物质提供通道，造成钢筋腐蚀和结构破坏，降低结构的耐久性[8]，因此对风机基础温度应力的研究具有重要意义。

本文选择圆形扩展风机基础，结合高邮某风电场实际工程，对风机基础的温度场和温度应力进行仿真计算分析，为风机基础的温控防裂提供参考。

1 研究方法

1.1 混凝土温度场计算

在求解三维非稳定温度场时，根据变分原理，热传导问题可等价转化为下列泛函的极小值问题，如式(1)所示：

(1)

式中：R为计算域；C为第三类边界条件的边界；T为温度，℃；a为导温系数，m2/h；θ为绝热温升，℃；λ为导热系数，kJ/(m·h·℃)；β为表面散热系数，kJ/(m·h·℃)；Ta为周围介质的温度，℃；τ为龄期，d[9]。

求解区域R划分为有限个单元时，根据泛函实现极值的条件，并对τ取差分格式，可得所有单元集合后的方程组，如式(2)所示：

(2)

式中：[H]为热传导矩阵；[R]为热传导补充矩阵；{T}τ+Δτ和{T}τ为结点温度列阵；{F}τ+Δτ为结点温度荷载列阵；Δτ为时间步长[9]。

根据式(2)，由已知的上一时刻的温度可求得下一时刻的温度。

1.2 混凝土应力场计算

混凝土的应变增量包括弹性应变增量、徐变应变增量、温度应变增量、自生体积变形增量和干缩应变增量[9]，如式(3)所示：

(3)

将结点力和节点荷载用编码法加以集合，得到整体平衡方程，如式(4)所示：

[K]{Δδn}={ΔPn}L+{ΔPn}C+{ΔPn}T+{ΔPn}0+{ΔPn}S

(4)

式中：[K]为整体刚度矩阵；{ΔPn}L为外荷载引起的结点荷载增量；{ΔPn}C为徐变引起的结点荷载增量；{ΔPn}T为变温引起的结点荷载增量；{ΔPn}0为混凝土自生体积变形引起的结点荷载增量；{ΔPn}S为干缩引起的结点荷载增量[9]。

1.3 仿真模拟计算

本文使用有限元计算软件ANSYS来进行仿真模拟计算。利用APDL并结合二次开发子程序UPFs高效地实现建立模型、输入参数、施加边界条件、输出计算结果，模拟施工过程，材料性能的变化以及外界条件的变化过程[10]，其中子程序usermat可根据应变增量计算应力增量；子程序USsBeg用于计算由温度徐变产生的节点力增量{ΔPn}C；子程序user01用于读入相关参数并获得单元信息；子程序user03用于温度计算；子程序user04用于Jacobian矩阵计算；子程序user05用于读入各步温度结果文件；子程序user07可获取当前所有节点温度；子程序user08用于输出全部节点应力最大值；子程序user09和user10用于输出温度和应力结果文件[11]。

由于温度场计算的初始条件对结果影响较大且难以确定，为得到准确的温度场初始条件，本文采取地基温度场提前计算一年的方法，将第365天的温度场作为正式计算的初始温度场。由于软基对结构温度变形的约束作用很小[12]，在保证计算精度的原则下，为提高计算效率，采用大模型计算温度场，小模型计算应力场的方法，将大模型计算的温度场结果转换为小模型的温度荷载，全过程模拟圆形扩展风机基础的温度场和应力场。

2 计算模型及参数

2.1 工程概况

某风电场位于高邮市临泽镇东南部，东临近兴化市。风机基础采用现浇钢筋混凝土圆形扩展基础。风电机组基础直径为20.00 m，圆盘厚0.80 m～2.50 m，埋深3.45 m，中墩直径7.00 m，中墩高度3.60 m，单个基础混凝土总量约为554.0 m3。地基为软基，主要由第四系全新统、上更新统冲积、湖积成因的粉质黏土、黏土、粉土等组成。

2.2 有限元模型

根据结构的对称性，取1/4基础进行实体建模分析。为得到精确的温度场计算结果，温度场计算模型包含土基、垫层、圆形扩展基础和覆土，温度场计算模型共含单元7 465个，节点8 768个，温度场计算有限元模型如图1所示。在应力场计算中仅考虑温度荷载和混凝土自重，应力场计算模型包含垫层和圆形扩展基础，应力场计算模型共含单元2 140个，节点2 734个，应力场计算有限元模型如图2所示。

图1 风机基础温度场计算模型

图2 风机基础应力场计算模型

由于风机基础位于地表以下，为得到准确的初始条件，将温度场计算模型材料参数全改为土基的材料参数提前计算一年，将第365天的温度场作为正式计算的初始条件。考虑模拟施工过程，材料性能的变化以及外界条件的变化过程，对温度场计算模型进行时程分析，得出风机基础从开挖、浇筑、覆土到运行的温度场，然后将各时刻温度场计算结果转化为温度荷载和自重施加到应力场计算模型上，得到风机基础的温度应力场。

2.3 计算条件与参数

此工程的计算条件如下：

施工开始时间为5月1日，风机基础土方开挖3 d后浇筑C20混凝土垫层，7 d后浇筑基础C40混凝土，15 d后覆土。浇筑温度取浇筑当日气温加2℃。温度场计算时间为1 110 d，应力场计算时间为1 095 d。考虑混凝土徐变和自生体积变形的影响。

本文在分析时所用的计算参数取值参考《混凝土坝温度控制设计规范》(NB/T 35092—2017)及实测数据，此工程的计算参数如下：

土和混凝土的主要热学和物理力学参数如表1所示。当地各月平均气温和风速如表2所示。

表面散热系数计算公式为：

粗糙表面：β=21.06+17.58v0.910

(5)

光滑表面：β=18.46+17.30v0.883

(6)

式中:v为风速[13]。

表1 土和混凝土热学和物理力学参数

表2 各月平均气温和风速

3 模型计算结果

在大体积混凝土结构中，温度应力的发展可分为三个阶段：(1) 早期：自混凝土浇筑开始，至水泥放热作用基本结束时止，一般30 d左右；(2) 中期：自水泥放热作用基本结束时至混凝土冷却到最终准稳定温度时，这个时期温度应力由混凝土的冷却及外界温度变化所引起，本算例中中期约为120 d；(3) 后期：混凝土完全冷却以后的运行时期，混凝土应力主要由外界气温的变化所引起[14]。

在此圆形扩展风机基础实例计算中，选取竖向剖面圆盘扩展部位表面节点和中墩部位中心节点，根据其温度和应力变化绘制出了相应部位的温度变化过程线和应力变化过程线，见图3—图6。通过遍历各部位温度和应力计算结果，选取各部位最大温度和最大应力，绘制出此风机基础的温度和应力包络线，见图7、图8。

图3 表面节点温度变化过程线

图4 中心节点温度变化过程线

由图3可以看出，此圆形扩展风机基础扩展部分表面节点温度会在浇筑后迅速升温至35℃左右，120 d后降至气温，然后随气温呈周期为一年的周期性变化。由图4可以看出，由于混凝土内部热量聚集，中心部位在浇筑后也迅速升温至65℃左右，之后温度下降至准稳定，以年为单位周期性变化。

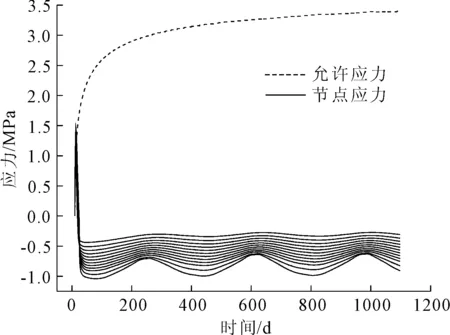
图5 表面节点应力变化过程线

图6 中心节点应力变化过程线

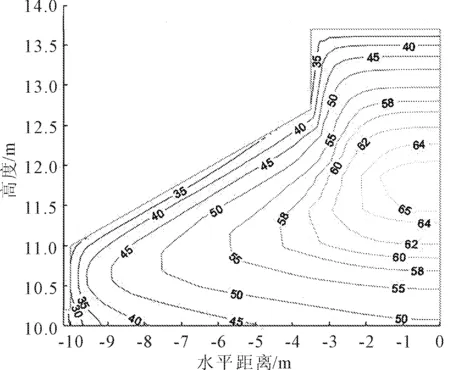
图7 竖向剖面最高温度包络图

图8 竖向剖面最大应力包络图

由图5可以看出，风机基础表面最大拉应力仅为1.5 MPa左右，但最大应力发生在早期，根据朱伯芳院士提出的混凝土极限拉伸变形与龄期的关系[15]可知，风机表面养护期内会出现温度裂缝，之后拉应力会逐渐减小，甚至变为压应力，限制表面裂缝的发展或使表面裂缝弥合。由图6可以看出，风机基础中心部位温度应力早期较小，但后期会增长至2.2 MPa左右。

由图7的温度包络线可知，此风机基础最高温度发生在中墩中部附近，最高约65℃。由图8的应力包络线可知，最大应力与最高温度类似，也发生在中心部位附近，最大约2.2 MPa。圆形扩展风机基础的最大温度应力和最高温度均呈由内向外递减。

4 结果分析

在圆形扩展风机基础施工过程中会产生大量水化热，而混凝土内表面散热不均匀，产生的温度应力不容忽视。初期虽然表面温度应力较小，但因混凝土发育不完全，仍有开裂的风险，经过分析发现内外温差和温度梯度与风机表面应力有很好的对应关系。后期风机中心部位会产生最大应力，圆形扩展风机基础中心部位温度最高时，应力并不是最大，反而中心温度降为准稳定后才出现应力最大值，为进一步探究风机基础中心部位最大应力与温度的关系，发现中心部位的温降值能更好的表现最大应力及发生的时间。

4.1 内外温差与应力关系

选取扩展部分混凝土表面和扩展部分混凝土中部区域，计算其温差。图9表示其温差和表面节点的平均应力变化趋势。由图9可看出，温差与表面平均应力的变化趋势相同。平均应力达到最大值1.15 MPa，1 d后，温差也达到最大值24.6℃。约100 d后，表面节点平均应力和温差均呈现周期性变化，同时达到极大值和极小值。

图9 表面节点内外温差与应力随时间变化图

4.2 温度梯度与应力关系

选取扩展部分混凝土表面区域，将其温度梯度和应力绘制成图10。由图9可知，在第61 d～158 d、358 d～545 d和718 d～911 d，内外温差为负值，即混凝土内部温度小于表面温度，其余时间内部温度均大于表面温度。结合图10可知，若温度梯度由内部温度大于表面温度引起，则应力与温度梯度同增同减；若温度梯度由表面温度大于内部温度引起，则应力与温度梯度变化趋势相反。

图10 表面节点温度梯度与应力随时间变化图

4.3 温降值与应力关系

中心部位的温降值指风机基础中心部位混凝土在达到最高温度后，混凝土各时刻温度与该部位最高温度的差值。由图11可以看出，风机基础中墩中部温降值和应力的变化趋势相近，中墩中部温度应力随温降值的增大而增大，随温降值的减小而减小。在第290 d附近，中墩中部温降值达到极大值51℃，温度应力值也达到极大值1.98 MPa。此后温降值和平均应力值按年进行周期性变化。

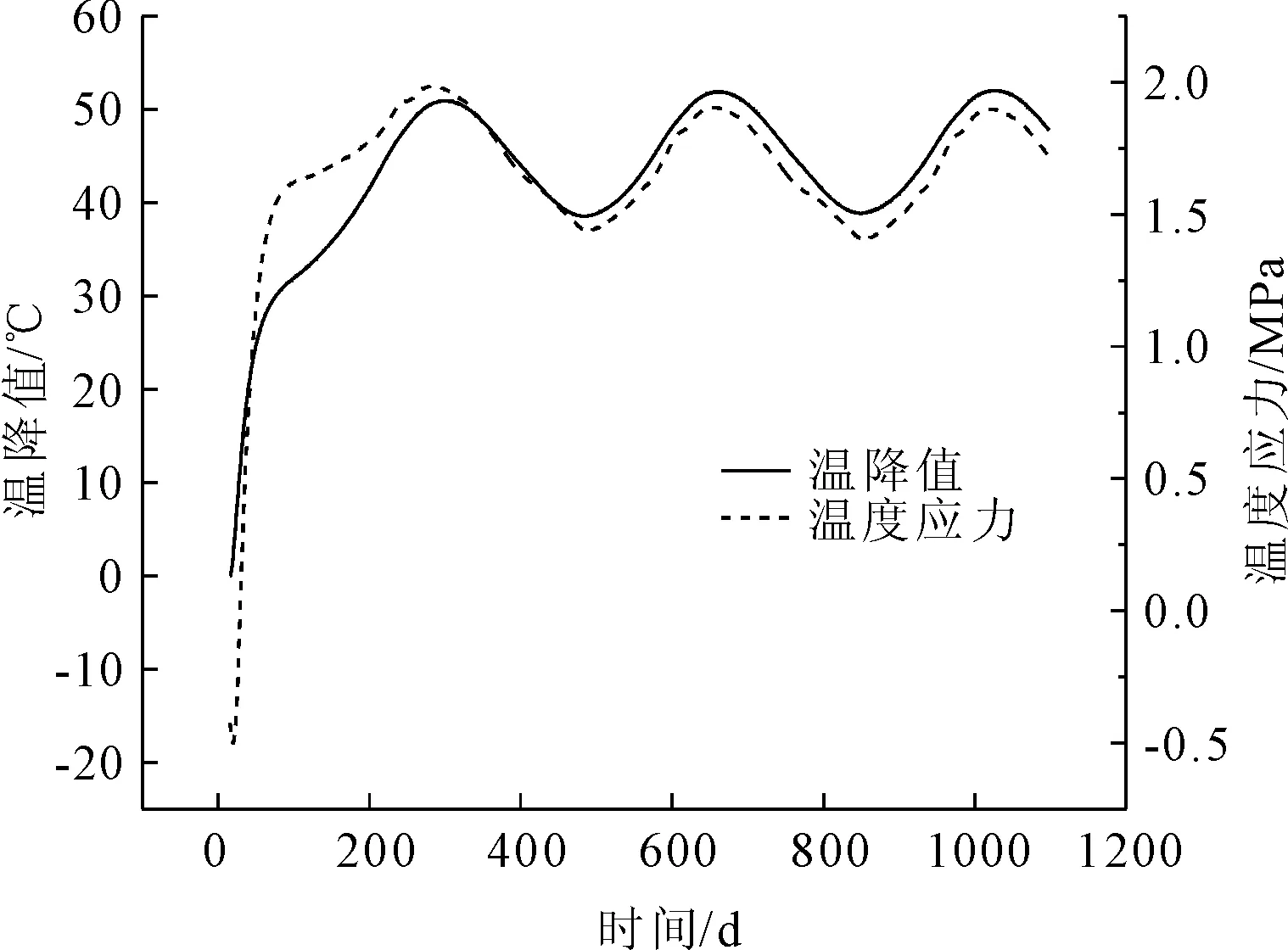
图11 中部节点温降值与应力值随时间变化图

5 结 论

通过对某圆形扩展风机基础温度场和应力场进行有限元计算，分析其温度场和应力场，可以得出以下结论：

(1) 圆形扩展风机基础混凝土浇筑期间产生大量水化热，内表散热不均匀，内部易热量聚集，故基础最高温度出现在中心部位，温度由内至外递减，之后基础各部位温度降至准稳定，随气温变化而周期性变化。

(2) 圆形扩展风机基础表面最大应力发生在早期，虽然数值不大，但此时混凝土未发育完全，可能会出现温度裂缝，之后拉应力会逐渐减小，甚至变为压应力，限制表面裂缝的发展或使表面裂缝弥合，危害较小。风机基础中心部位最大应力发生在后期，数值较大，不易观察且危害严重，应当警惕内部温度裂缝的产生。

(3) 圆形扩展风机基础表面附近的内外温差和温度梯度与表面应力、中心部位的温降值与应力均有很好的对应关系。表面附近的内外温差与表面应力同增同减。温度梯度由内部温度大于表面温度引起时，表面应力与温度梯度同增同减；温度梯度由表面温度大于内部温度引起时，表面应力与温度梯度变化趋势相反。中心部位的应力与温降值变化趋势相同。因此可以通过控制中心部位的温降值、表面附近的内外温差和温度梯度来控制风机基础温度应力。