基于Harris衰减函数的岩石单调加载本构模型
2022-05-17许志雄
许志雄,范 炜
(1.福州职业技术学院 建筑工程系, 福建 福州 350108;2.福建江夏学院 工程学院, 福建 福州 350108)
随着我国经济与科学技术的发展,向地下要空间则是未来发展的重要方向之一[1],这势必涉及到大量的岩石工程。岩石变形是影响岩石工程安全的重要因素,因此掌握岩石的力学本构模型对更好利用地下空间具有重要意义。Krajcinovic等[2]在Lemaitre[3]提出的等效应变假说基础上,结合了连续损伤和统计强度理论,建立了损伤模型,后人在此基础上不断完善改进,提出了多种统计损伤模型。高玮等[4]将破裂岩石视作多个小立方体,并假定各个立方体的强度服从Weibull 分布,从而提出一种破裂岩体的本构模型。曹瑞琅等[5]在岩石微元强度服从Weibull 分布的基础上,考虑了岩石残余强度并对损伤变量进行了修正,最终建立了考虑岩石峰后残余强度的本构模型。蒋浩鹏等[6]则将温度考虑进来,得到了高温后岩石统计损伤本构模型。 Li等[7]和王林峰等[8]则认为岩石强度服从正态分布,并基于此建立了新的本构模型。然而 Weibull 分布存在尺寸效应,而正态分布则会出现岩石强度和参数为负值的现象,这与实际情况不符。因此,部分学者尝试采用新的函数构建岩石统计损伤模型,其中效果比较理想的是Harris函数。黄海峰等[9]假设岩石微元强度服从Harris函数,并对损伤模量进行修正,构建了损伤软化模型。王创业等[10]和李小峰等[11]同样认为岩石微元强度服从Harris分布,建立的本构模型与试验结果匹配度较好。但上述理论涉及到的岩石微元强度存在不易测量的缺点,而且,部分学者采用拟合法确定模型参数,虽然拟合度较好,但参数物理意义不明,而这势必影响本构模型的应用。大量试验表明,岩石在单调加载过程中,随着应力增大,应变快速增加直至岩石破坏,其对应变形模量表现出逐渐衰减的特征。变形模量作为岩石基本物理量之一,测量简便[12],如果能够获得变形模量的衰减规律,就可以建立应力与应变之间的关系。因此,本文通过引入Harris函数来表征变形模量衰减规律,并通过极限求导的方式获得模型参数。通过与已有试验数据进行对比,验证了新模型的适用性。
1 本构模型分析
1.1 理论模型
图1所示为岩石典型单调加载应力应变曲线。
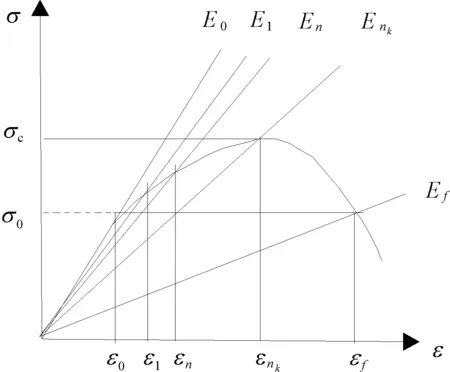
图1 岩石单调加载应力应变曲线
考虑压密段岩石应力较低,故忽略岩石压密过程。假设在ε0之前岩石处于线弹性段,随后岩石进入弹塑性阶段,随着应力增加,应变大幅增加,应力应变曲线逐渐偏离纵坐标。选取原点作为起点,根据变形模量定义可获得不同应力应变处变形模量如图1所示。
若将ε0至εf段应变进行Nf等分,则第n段应变为:
(1)
式中:ε0为弹性终点处应变值;εn为第n等分处应变值;εf为单调加载破坏处应变值;n为第n等分;Nf为弹性段终点至破坏点等分总数。在单调加载过程中变形模量从E0逐步衰减到Ef后,岩石破坏。已有成果常采用式(2)定义岩石损伤[13-14]:
(2)
式中:Dn为岩石第n等分处损伤值;En为第n等分处变形模量;E0为初始变形模量。
根据公式可知当岩石破坏时,岩石损伤并不等于1,即岩石不会破坏,这与实际不符。为此,将变形模量进行归一化,如式(3)所示。
(3)
式中:Kn为变形模量归一化值;Ef为岩石加载破坏处变形模量;E0,En意义同上。
由此可知,随着单调荷载的增加至岩石破坏,变形模量归一化值则从1衰减到0。若能利用一个函数来表征衰减规律,则可以获得变形模量数值,从而得到应力应变关系。常见衰减函数有线性衰减,指数衰减,高斯衰减以及Harris衰减等。显然对于单一线性衰减其衰减速率为恒值,若要满足衰减速率为变量则要构造分段线性函数,过于麻烦;指数衰减是先剧烈衰减然后变缓,难以满足不同类型岩石的变形模量变化规律;高斯衰减速率是先缓慢,然后变快,最后又放缓呈钟形,同样难以满足不同类型岩石破坏,且高斯衰减计算相对繁琐,参数可为任意实数,这与实际情况不符[15]。反观Harris函数,见式(4),仅有2个参数且均大于0,通过变换两个参数的值可以得到不同形状的衰减形式。
(4)
式中:X为函数自变量;a,b为大于0的常数。
为了建立变形模量与等分段数之间的关系,可令X=n/(Nf-n),则当n=0,S(0)=1,当n=Nf时,S(Nf)=0,从而得到用衰减函数表征归一化变形模量的表达式:
(5)
根据式(5)可以求得εn处对应的变形模量为:
(6)
从而可得:
(7)

B=(E0-Ef)·ε0
D=Ef·ε0
1.2 模型参数确定
根据式(7)可知,岩石单调加载过程中应力与分段数n(由应变确定)存在一一对应关系,是分段数n的函数。假定岩石全应力应变曲线峰值σc对应分段次数为nk,则该点满足边界条件有:
(8)
式中:σc为峰值应力;nk为峰值应力对应的应变分段数根据式(8)中第一项可得:
(9)
根据式(8)中第二项可得:
(10)
根据式(9)和式(10)可得:
(11)
(12)

通过对式(12)变换则有:
(13)
由式(11)可得:
(14)
由此解得:
(15)
联立式(13)和式(15)可得:
(16)
(17)
2 本构模型验证
为验证所建立的岩石本构模型的适用性,根据文献[16-19]试验数据进行计算,得到本构模型参数如表1所示,最终结果如图2所示。
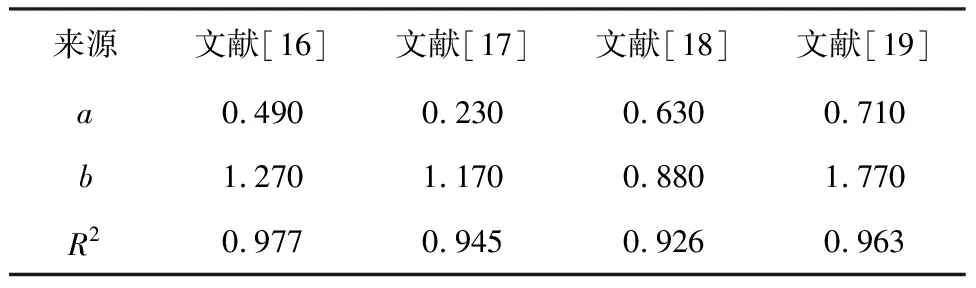
表1 模型参数值
从图2可以看到,本文所提出的本构模型理论值与试验值吻合度较高,尤其在峰前段高度重合,在峰后段存在一定偏差,当岩石在峰后段应力快速降低时,二者吻合度较差,对于该问题,需进一步研究。但在岩石工程中,一般利用的都是岩石峰前段承载能力,因而本文所建立的模型能够满足工程应用。
3 模型参数分析
为了进一步讨论模型参数对理论解的影响并分析参数的物理意义,以文献[15]为例,通过改变参数a和b的值,来分析模型参数对结果的影响,结果如图3所示。

图2 本构模型验证
从图3(a)中可以看到当参数b保持不变,随着参数a的增大,峰值应力出现较为明显的下降,当参数a由0.5增大至2.0时,峰值强度由72 MPa逐步降低至54 MPa,与参数a基本呈线性关系。与此同时,岩石峰值应变也随着参数a的增大而减小,而参数a的变化对岩石峰后曲线形态没有明显影响,这即表明参数a与岩石峰值强度相关。而从图3(b)则可以看到,当参数a保持不变,随着参数b的增大,峰值应力和峰值应变均增大,但增大幅度较小。但参数b对岩石峰后曲线形态影响较为明显,随着b的增大应力应变曲线由较为平缓状转变为陡直状,峰后应力跌落速度加快,表明岩石脆性增强。故经上述分析可知,模型参数a主要反映了岩石的宏观强度,而参数b则在一程度上体现了岩石的延脆性。
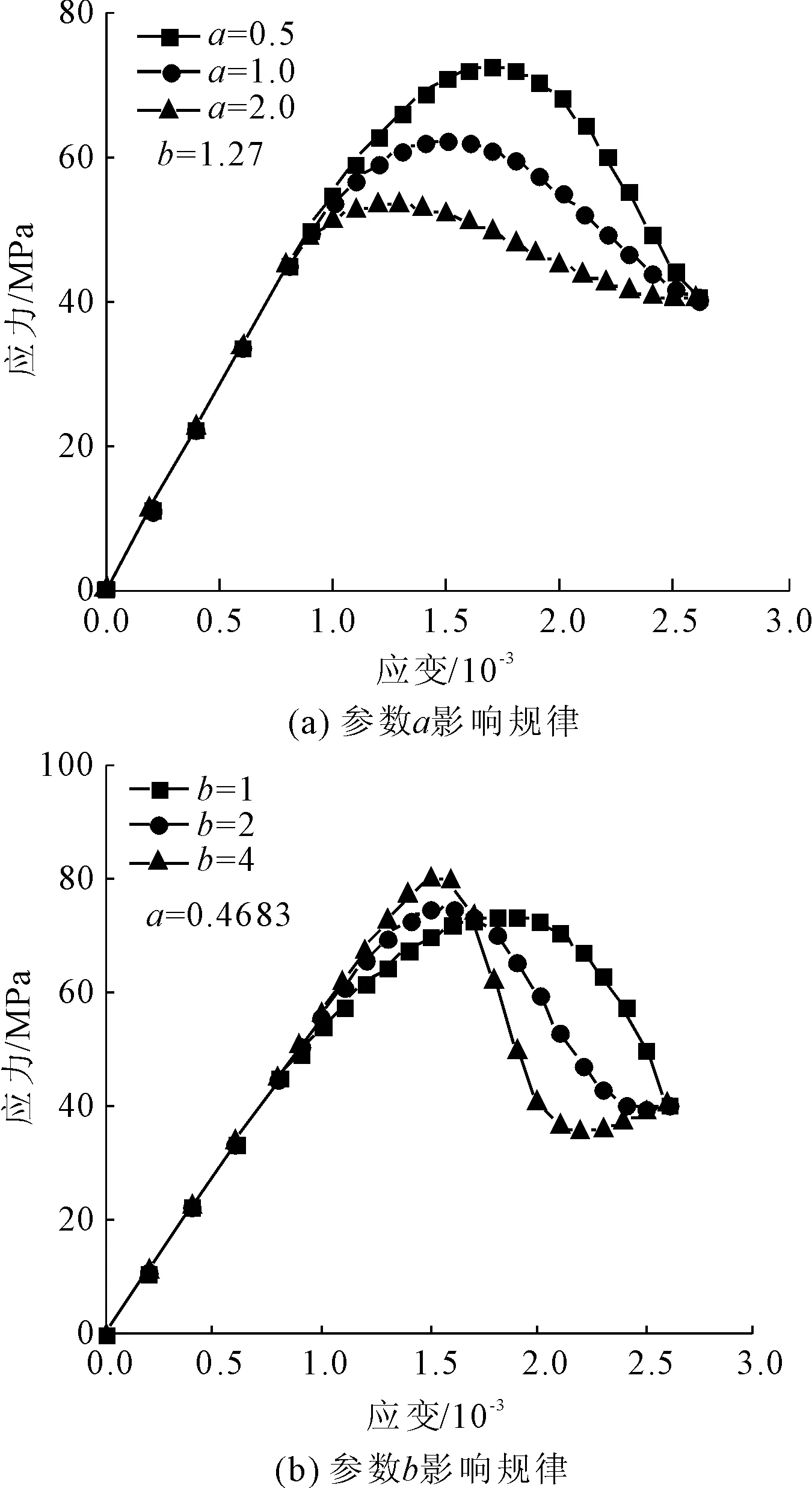
图3 模型参数分析
4 结 论
(1) 以变形模量为研究对象,通过分析变形模量在单调加载过程中随着应变增大而衰减的特征,引入Harris函数来表征变形模量衰减规律,构建了岩石单调加载本构模型。
(2) 采用极值理论,结合试验曲线特征值,推导了模型参数的计算表达式,模型参数物理意义明确。与前人试验结果对比,验证了本文模型的正确性。
(3) 模型参数分析表明,参数a控制岩石强度,a值越大,岩石峰值强度越低。参数b与岩石强度关系不大,主要与岩石延脆性相关,b值越大,脆性越强,反之延性越明显。
