红砂岩浮力折减系数研究

2022-05-17张孝斌朱彦鹏赵小明

水利与建筑工程学报 2022年2期

黄瑞，张孝斌，朱彦鹏，赵小明，王浩

(1.甘肃第六建设集团股份有限公司，甘肃兰州 730050；2.甘肃省建设投资(控股)集团有限公司，甘肃兰州 730050；3.兰州理工大学土木工程学院，甘肃兰州 730050)

由于红砂岩特殊的工程性质，兰州地铁深基坑开挖过程遇到了一系列问题。红砂岩的特殊性在于：红砂岩砂形疏松，胶结性能弱，透水性强，易风化。近年来有许多学者对红砂岩地基进行了大量研究，但在浮力折减系数方面研究甚少，对兰州特殊红砂岩的研究更是少之又少。因此，进行兰州地区红砂岩地基浮力折减系数研究将具有很高的工程价值，这也将为今后兰州地区深基坑开挖、设计等工程提供一定的理论依据。

地下空间的利用与开发一直是研究的热点，舒昭然等[1]开展了在水浮力作用下地下室底板变形机理的研究，提出了地下室底板上浮破坏的防治措施。刘振宇等[2]通过对强风化砂岩的研究，拟合出渗透系数k的经验公式，为抗浮设计提供了一定的依据。对弱透水性地层浮力“折减”方面的研究，国内不少学者认为不能用孔隙率作为折减依据[3-5]，一些学者通过试验研究得出黏性土的折减系数主要在0.6～0.8之间[6-9] 。梅国雄等[10]利用模型试验，得出砂土层地下水浮力不存在折减，而黏土层地下水浮力折减系数为0.7。潘曾志[11]认为基底与建筑构地基的接触方式会影响浮力折减系数，当渗流路径通过砂岩渗入基底时，折减系数为0.31～0.47；当通过砂岩地基内部细小通道时，折减系数取0.63～0.73。王露[12]以兰州地铁车站抗浮为背景，通过室内外试验，最终确定红砂岩浮力折减系数为0.30。宋林辉等[13]通过对实验装置进行改进，得到地下结构在软黏土中的浮力折减系数很小，仅为0.93。刘博怀[14]利用模型试验分别得出不同渗透系数的灰土地基、黏土地基及粉土地基的折减系数依次为0.75～0.79、0.63～0.70、0.85～0.94。张中杰等[15]以珠海市海积流塑淤泥质黏土为研究对象得出地下结构浮力折减系数为0.8。陆启贤等[16]应用自制的试验模型装置，对模型桶进行了上浮试验和孔隙水压力传递试验，得出在黏土中的浮力折减系数取值范围为0.84～0.87。

本文在综述研究成果的基础上，改进试验装置，考虑渗流影响，通过模型试验和数值模拟相结合的方法研究红砂岩浮力折减系数。

1 试验方案

1.1 试验设备

整个试验用到的主要设备有：试验模型坑(外箱)，如图1所示，其尺寸分别是:长与宽相等为1.8 m，高度为1.5 m，箱体采用双面焊缝，其铁皮厚度为5 mm，并且在内部填铺单一土质以此来模拟地基；试验模型箱(内箱)，如图2所示，模型箱的高度为0.6 m,铁皮厚度为3 mm，质量为64.2 kg。其中上顶面的开口边长均为1.4 m，底部则采用边长为0.2 m的正方形铁皮通过双面焊缝进行完全封闭，模型箱侧壁与水平地面呈45°的倒梯形台代表地下结构；传感器(微型土压力盒和孔隙水压力计)；XL2101C程控静态电阻应变仪以及其他辅助设备。

图1 试验模型坑

图2 试验模型箱

表1 试验用土的基本物理参数

1.2 试验设计

(1) 避免侧摩擦阻力的产生：为了使侧壁产生较小的土压力，试验模型箱的侧壁采用45°倾角，并且在侧壁表面均匀涂抹一层凡士林，不仅防止侧壁渗水进入模型箱底部，还降低了侧壁的摩擦系数；当摩擦系数和土压力均很小时，侧壁摩擦阻力也较小。在不考虑侧摩擦阻力影响的情况下，可得到准确的浮力折减系数。因此，可以在工程实践方面提供理论依据，降低工程成本。

(2) 避免产生负压力：为消除地基土与模型箱底部接触产生的负压，在其模型箱底部刷一层建筑砂浆。

(3) 箱子浮起点的确定：试验中采用的微型孔隙水压力计和土压力盒均匀埋在结构模型箱底部中心，如图3所示。每隔30 min从装满水的模型箱中排水12.5 kg，在排水过程中，孔隙水压力计和土压力盒的读数不断变化。当两者的实测值相等时，即可确定模型箱浮起点。

(4) 传递路径的完整性：将地基土与模型箱外侧表面充分密切接触，防止产生不均匀固结、沉降，以此来确保孔隙水压力在发生渗流时可以形成完整的传递路径。

图3 传感器分布图

1.3 试验步骤

本次试验土样取自兰州市轨道交通1号线东方红地铁车站基坑，土样较纯，粒径均匀，可塑性好，可直接用于填铺。

(1) 填铺地基土

① 试验模型坑内应分层铺0.50 m厚的红砂岩，并且压实均匀，其中每层铺填0.25 m。在距离模型坑内壁半米处的位置旁用记号笔做上标记，以此用来作为将试验模型箱稳定搁置于地基土上的控制标准。为了将试验模型箱底部平整的置于模型坑，就需要四周铺填的地基土同一时间达到标记线。在位于填筑铺层地基土的中心处分别均衡的铺排6个土压力盒和2个孔隙水压力计，对其进行埋设并进行编号。

② 在确保试验模型箱与试验模型坑中心处底部对齐的情况下，将试验模型箱放置在地基土上。应用平整度检测仪进行测量、微调并且将模型箱固定好。模型箱与模型坑之间的缝隙用地基土进行分层铺填，其中铺填高度与模型箱高度相同。

(2) 采用饱和土体

① 向试验模型箱内持续注水，直至水从模型箱周围均匀溢出。当水位高于土面后，关闭水阀，沉淀放置一段时间。

② 静置20 d之后，每天测量其水位高度，待水位高度变化量为零时，表明此时土体完全饱和。将模型箱中多余的水排除后，即可进行测试。

(3) 抽水及其数据收集。将传感器线接到电阻应变片的接线端，每次的抽水质量为12.5 kg，且每隔0.5 h进行一次抽水，直至模型箱内的水被完全排除。对整个试验过程中孔隙水压力计和土压力盒所产生的数据进行采集记录，反复几次，取均值。

(4) 分析数据。对上一步骤采集的实验数据进行计算分析，从而可以得到模型箱的上浮时间，此时刻所产生的浮力即为模型箱的实际浮力数值，将其再与理论浮力数值进行对比，两者之间的比值就是其折减系数。

计算公式表达式如式(1)所示：

(1)

其中：η为浮力折减系数；F浮为模型箱上浮时刻受到的实际浮力数值；F浮理为模型箱在纯水环境下所受到的理论浮力数值。本试验中F浮理始终为一定值，亦：

V排=0.456 m3

F浮理=ρ液gV排=4.56 kN

对采集记录的试验数据通过分析计算可得到抽水次数、模型箱中剩余水质量、模型箱和箱中剩余水总质量之和、模型箱内剩余水位的高度及其浮力折减系数值之间的相互对应关系，详情见表2。

2 试验数据处理

2.1 受力分析

在不考虑侧摩阻的情况下，如图4所示的概化模型图，模型箱同时受到四种力共同作用，平衡关系成立，其表达式见式(2)：

(2)

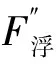
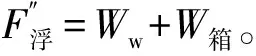
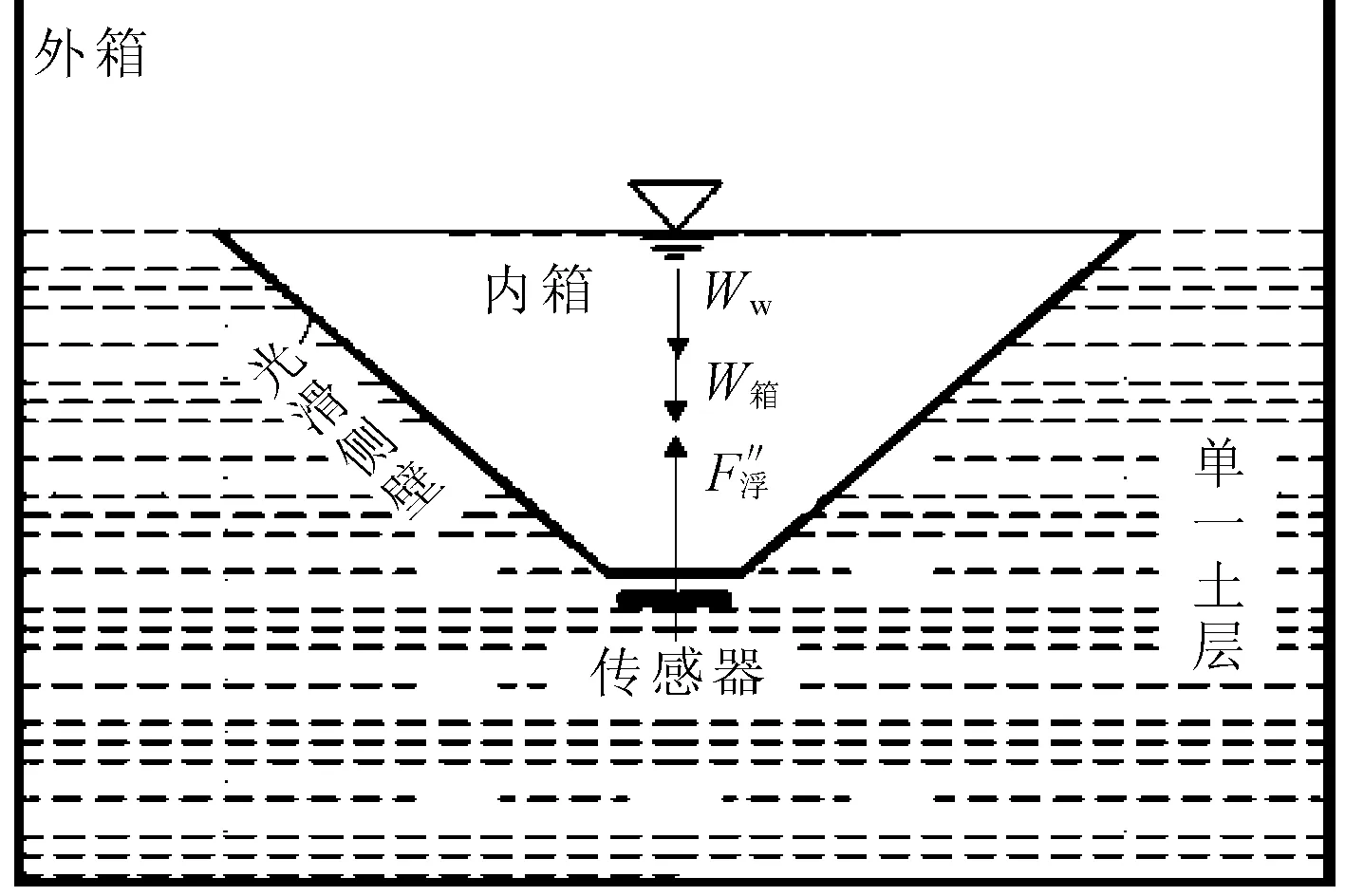
图4 试验装置概化模型图

表2 抽水次数、模型箱中水质量等与浮力折减系数对比表

2.2 试验结果分析

试验完成后，绘制模型箱中水位高度、箱底微型孔隙水压力计及土压力盒实测值的曲线关系图形。

(1)微型土压力盒实测值分析。如图5所示，埋设在地基中的微型土压力盒实测值与模型箱水位高度的变化规律曲线基本上是重合的，其拟合程度较高。

图5 S1—S6内箱水位高度与土压力盒实测值关系曲线

(2) 微型孔隙水压力计实测值分析。如图6所示，埋设在地基中的微型孔隙水压力计实测值的下降速率随着模型箱中水的抽出而逐渐变缓，当曲线斜率为0时，此时箱底孔隙水压力可以使模型箱浮起。

图6 P1—P2内箱水位高度与孔隙水压力测量值关系曲线

当模型箱开始浮动时，根据表2查出模型箱内水位高度为0.377 0 m～0.390 4 m。虽然实际浮力数值范围为2 076 N～2 201 N，但理论浮力值为4 560 N。根据计算公式(1)，得出浮力折减系数的取值范围为0.455 3～0.482 7，取均值0.469 0作为本次试验的折减系数。此研究结果可为今后兰州地铁站的防浮设计提供一定的理论依据，并可节省工程造价。

3 数值模拟分析

采用COMSOL Multiphysics多物理场软件，模拟条件和试验条件相同，对试验后的红砂岩地基浮力值进行数值模拟，将模拟结果与试验结果进行比较，对有限元模型的精确性、有效性进行验证。

3.1 有限元模型的建立

(1) 数值模型的基本假定：① 小变形；② 地基土：完全饱和、单一均质、各向同性；③ 土体内部孔隙水渗流时，流动状态为层流；④ 土颗粒与水均不可压缩；⑤ 环境等外界因素对试验材料的影响忽略不计。

(2) 建立流固耦合的数学模型。用COMSOL中的达西定律分析模块对孔隙水在饱和土体内的流动进行分析，则流体质量连续性方程表达式如式(3)所示：

(3)

其中：ρf为液体密度；uf为流体的压力，压正拉负；S为流体储存系数；g为重力加速度；k为渗透系数；D为位置高程；Qm为源汇项。

为了可以准确地反映饱和土体中流体体积变化是由单位流体压力变化而导致的，故将储存系数代入到流体质量连续性方程。

储存系数如式(4)所示：

(4)

αB=1-Kd/Ks

(5)

其中：S为储存系数；n为土体孔隙率；Kf为流体体积压缩模量；αB为比澳系数；Kd为土骨架体积的压缩模量；Ks为土颗粒的压缩模量。

对于地基土材料来说，因为Kd≤Ks，故取αB≈1。式(3)的源汇项Qm更改为-αBρf(∂u/∂t+∂v/∂t+∂w/∂t)以耦合固体对流体带来的影响。土体的应力符号规定为拉正压负，且只表示方向并不表示大小。(∂u/∂t+∂v/∂t+∂w/∂t)>0表示在饱和土中有外界水流入，故改变源汇项Qm的符号，取为负号。

采用有效应力的原理以耦合流体对固体带来的影响，此表达式的计算公式如式(6)所示：

σ=C∶(ε-εth-εp)-αBufI

(6)

其中：σ为总应力张量，拉正压负；I表示单位张量；C为在排水条件下所得到的弹性张量。

从式(6)中得出，将孔隙水压力uf从第一、第二和第三主应力计算式中同时扣除，就会得到土体的有效应力。

(3) 立体模型的建立。立体模型的长宽高依次为：1.8 m×1.8 m×1.1 m，见图7。

图7 立体模型图

(4) 物理场的选取。在COMSOL软件中应用的物理场有两种：

① 固体力学。此界面不仅可以模拟结构的一维、二维问题，而且还可以进行三维结构的模拟。特别注意的是，在进行二维结构的模拟时，为了进行优化，可以简单的将其作为平面应力、应变问题进行处理。界面内置的Navier-Stokes方程可用于求解应力、应变和位移的结果。

② 达西定律。此界面则用于流体在低速流动时通过孔隙率或者渗透率均很小的多孔介质中孔隙流动的分析，其中压力梯度是影响驱动力大小的主要因素。

用水头高度和时间t之间的关系来表示int1(t)插值函数，将地面视为绝对压强的基准面，每隔30 min排放出相同质量的水，以此来模拟整个试验的排水过程，其水头变化如图8所示。

图8 水头高度随时间变化的插值函数

(6) 边界条件的设置

① 固体力学边界条件。图9表示了固体力学边界的设置情况，其中固定约束为边界8，辊轴约束为1、3、4、5和7边界，自由边界为边界2和6边界。为了将模型简化，把内箱的自重分散到其接触的每个边界上。

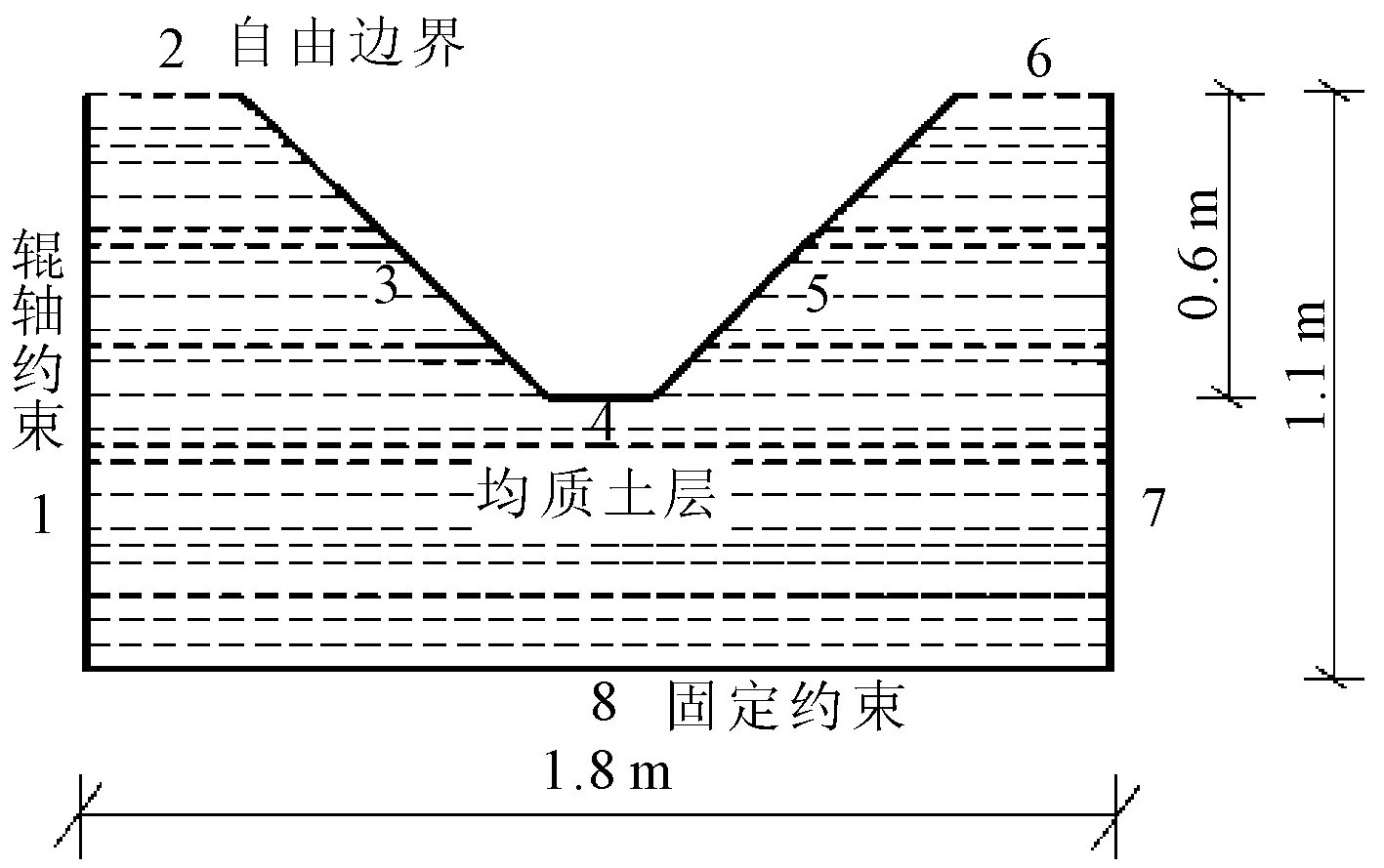
图9 固体力学边界设置图

② 达西边界条件。如图10所示，显示了达西边界的设置情况，布局重力节点，其中不透水边界用1、3、4、5、7和8边界表示，p=0边界为2和6边界；将边界8设为基准面，总水头则为1.1 m，插值函数int1(t)表示箱内水头高度。

图10 达西边界条件设置图

(7) 网格划分。因为此研究涉及流体的流动，为了提高计算的精度，故采用六面单元体来进行网格的剖分。选取体扫掠作为模型的网格划分，图11为具体网格细化示意。其中，网格包括了8个三角形，32个顶点单元，553个边单元，3 353个四边形，6 243个六面体。

图11 网格细化图

3.2 模拟结果分析

为了使地基土中的孔隙水压力和有效应力更直观的看到其具体分布，在后处理的时候提取模型箱的底部中心的切面y=0.9 m来替换整个模型，有限元模型的坐标为x,y,z(0.9,0.9,0.5)。因为土压力盒只可以测量饱和土的总压力值，但是试验中采用模型箱底部的土骨架对其传递的力刚好是“0”来作为判断箱子的上浮瞬间标准。因此，土体的有效应力σ′即为从软件中构建的第一、第二和第三主应力表达式中依次分别扣除孔压之后，所得到的第一主应力。在模拟软件中，土体受力的正负号规定为拉正压负，而流体受力的正负号规定刚好与土体相反。借助COMSOL软件对红砂岩浮力折减系数进行模拟，位于模型箱底部中心处的有效应图如图12所示，当底部中心处的有效应力为零时，模型箱此时刚好处于飘浮状态。其中，最大拉应力1×104Pa出现在最顶端，最大压应力2×104Pa出现在最底部，从图中可以看出：整个土体在垂直方向上，绝大部分区域被压缩，称为固结段。位于模型箱底部中心处的孔隙水压力图见图13，顶端的孔隙水压吸力数值为0.2×104Pa表示土体在拉力的作用下而达到屈服；压力数值为1×104Pa，表示在抽水过程中土体逐渐固结。分析结果与试验中所看到的现象大体一致，从而说明此模型的可靠、准确性。

图12 位于模型箱底部中心处的有效应力图

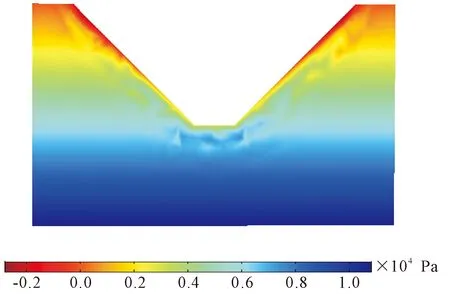
图13 位于模型箱底部中心处的孔隙水压力图

图14表示位于模型箱底部中心处地基土的有效应力值随着模型箱水位高度降低的变化曲线。当模型箱的水位高度为0.383 7 m时，在此水位下，模型箱受到的浮力实际值为2 135.8 N，因其理论浮力值为4 560 N，故由式(2)计算所得到的折减系数为0.468 4。图15表示位于模型箱底部中心的孔隙水压力数值随着内箱水位高度降低的变化曲线。

图14 位于模型箱底部中心处的有效应力曲线图

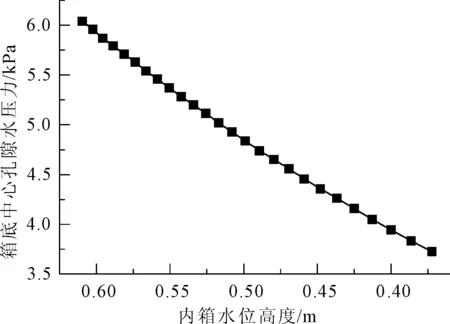
图15 位于模型箱底部中心处的孔隙水压力曲线图

将浮力折减系数试验实际测量值于与模拟值进行对比后发现：(1) 室内试验实际测量值与模拟的总压值较为接近，并且孔压的变化规律曲线能够较好的吻合；(2) 通过试验所得到的浮力折减系数为0.469 0，然而经模拟分析得到的浮力折减系数为0.468 4，实测值与模拟值较为接近。因此，体现出基于流固耦合理论所建立的有限元模型的正确、合理性。