基于冲击能量的管簧式起落架优化设计

程 成，张 华，丘晓安

(重庆大学航空航天学院，重庆 400044)

飞机在着陆过程中会承受巨大的冲击载荷[1-2]。作为飞机重要承力部件的起飞着陆系统，在涉及飞机安全的起降过程中，担负着极其重要的使命。通用飞机的固定弹簧式起落架一般包括管簧式和板簧式，具有结构简单、可靠、维护方便的特点，广泛用于小型私人飞机。

有别于流体弹簧缓冲器，固体弹簧缓冲器的吸能情况完全不同。为研究固定弹簧式起落架的着陆性能，邓扬晨[3]以杆件的强度与失稳载荷作为极限条件，采用位置优化与尺寸优化进行起落架结构的最小质量设计，仿真结果与实验结果相符合。薛志鹏等[4]采用模态分析法，调整刚度矩阵等效边界约束条件，获得扁簧式起落架约束模态数据，建立状态空间模型以描述起落架的动力学特性。王力等[5]将板簧式起落架看作外伸梁，通过满应力反向迭代设计，实现用最小质量代价满足缓冲吸能的目标。贾玉红等[6]设计了管簧式起落架落震试验，通过改变下落高度和投放质量以及机轮带转等参数，得到管簧式起落架的相关落震性能参数。徐尧等[7]建立了起落架与弹性机体的多柔性全机模型，通过分析起落架着陆响应载荷，发现机身垂向一阶弯曲模态对着陆载荷影响最为显著。以上论文从不同角度对固定弹簧式起落架进行了研究，但未对弹簧式起落架的形状进行优化设计。

本文从固定弹簧式起落架将冲击能量转化为弹性应变能的角度出发，对起落架进行受力分析，得到起落架在冲击载荷下的弹性应变能模型，并采用遗传算法对起落架管簧的形状进行优化设计，最后利用ABAQUS对起落架进行有限元着陆仿真，验证起落架着陆性能优化效果。

1 起落架地面载荷及缓冲性能分析

1.1 管簧式起落架冲击载荷分析

通用飞机的固定弹簧式起落架有多种形式，本文研究的起落架主支柱是管簧，在优化模型中忽略机轮的影响。管簧对称面与垂直面夹角为α，着陆过程中，起落架受到地面的冲击载荷可分解为航向F1、横向F2和垂向F3。为了便于分析，将原飞机的坐标系绕Y轴旋转角度α，使管簧处于Z1-Y1平面内。图1所示为管簧受力简图，作用在管簧与机轮连接端的载荷Fx,Fy和Fz由F1,F2和F3绕Y轴旋转角度α得到。

图1 管簧受力简图

飞机的着陆过程是指从降至安全高度到停止滑跑为止，一般包括下滑、拉平、平飞减速、飘落和地面减速滑跑等阶段[8]。整个着陆过程，起落架起作用的阶段有飘落阶段和地面减速滑跑阶段。

飘落阶段，假设飞机对称着陆，取单个起落架的着陆当量质量Wm为飞机最大着陆质量的一半[1]，则单个主起落架的垂直载荷系数nz[8]为：

(1)

由式(1)即可得到单个主起落架在飘落触地时地面载荷的垂向力F3为：

F3=nzWmg

(2)

式中：g为重力加速度。

三点着陆不带刹车滑跑时，机轮转速与机身保持相对静止，此时载荷由式(3)算得[1]：

(3)

式中：l1,l2分别为飞机重心至前机轮接地点的水平距离与至主机轮接地点的水平距离；WTO为最大起飞质量。

三点着陆带刹车滑跑时，考虑前轮无刹车的情况，则主起落架上的载荷[1]为：

(4)

式中：H为飞机重心至地面高度。

1.2 管簧式起落架缓冲性能分析

起落架由飞机自身质量引起的垂向位移Δst，称为起落架静位移，假设飞机的下沉速度为vz，则对地面的冲击载荷为FPd[9]：

(5)

(6)

式中：M(x)，T(x)，FN(x)分别为在x处起落架所受弯矩、扭矩和轴力；E为弹性模量；G为剪切弹性模量；I为惯性矩；IP为极惯性矩；A为横截面面积。

C点作用力Fx和Fz使起落架产生弯曲变形，取管簧某段为ds，则该段受到的弯曲应变能dU弯如式(7)所示：

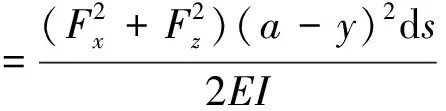
(7)

式中：a为管簧BC部分水平投影长度；y为横坐标自变量。

图1中的管簧轴线用曲线z=f(y)表示，并假设ds微段的坐标是(y0,z0)，则过该点的切线与力Fx的距离为扭转力臂，如此该段的扭转应变能dU扭为：

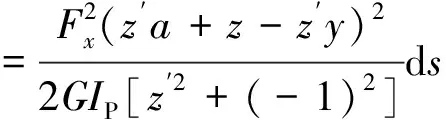
(8)

式中：z′为函数z的导数。

当飞机着陆时，管簧变形产生轴向应变。若ds段的切线与Y1轴的夹角为β，同时材料变形在线弹性范围内，则轴向应变能dU轴为：

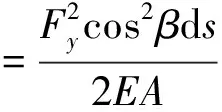
(9)

式中：β=arctan|z′|。

2 优化模型

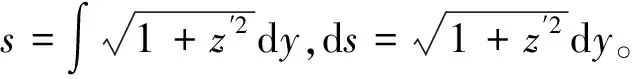
(10)

式中：Dmin,Dmax分别为C,B处管簧的外直径，Dmin=34 mm，Dmax=52 mm；a为管簧BC部分水平投影长度，a=962.5 mm；d为管簧内直径，d=28 mm。则应变能可表示如下：

(11)

式中：I(y)为y坐标处管簧惯性矩；IP(y)为y坐标处管簧极惯性矩；A(y)为y坐标处横截面积。

设式(11)中的z=f(y)，为多项式函数，如式(12)所示：

z=a0yn+a1yn-1+a2yn-2+…+an-1y+an

(12)

式中：ai(i=0,1,…,n)为多项式系数。

管簧的B点与机身相连，C点安装机轮，为避免角度过大产生局部应力集中，要求在此两点处平滑过渡。至此得到起落架外形优化模型：

(13)

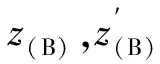
3 优化设计

缓冲装置吸收能量过程中的过载系数应该控制在较低范围(2.0～4.0)内[8]，故设起落架最大过载不超过4。某型飞机的前机轮与飞机重心在水平上的距离l1=1 500 mm，后机轮与飞机重心在水平上的距离l2=500 mm，飞机重心高H=600 mm，将数据代入式(2)、式(3)、式(4)得到飞机着陆时的载荷情况，可以看出在飘落阶段，起落架将受到最大的冲击载荷，目标函数的载荷将由该阶段的着陆情况确定，见表1。

优化过程即找到起落架管簧支柱吸收最大应变能的外形。与机身相连部分以及轮轴部分刚度较大、变形很小，设为刚体，本文只针对BC部分采用遗传算法对起落架进行优化。遗传算法由D.E.Goldberg在一系列研究工作中归纳总结而成，是模拟生物在自然界中的遗传和进化过程而形成的一种并行、高效的全局搜索方法，对处理非线性复杂函数有高度的优越性[10]。本例中设起落架外形函数分别为3，4，5次多项式，用MATLAB中的遗传算法对目标函数全局寻优，最终得到起落架的外形函数，如图2所示。

表1 起落架各工况下载荷情况 单位：N

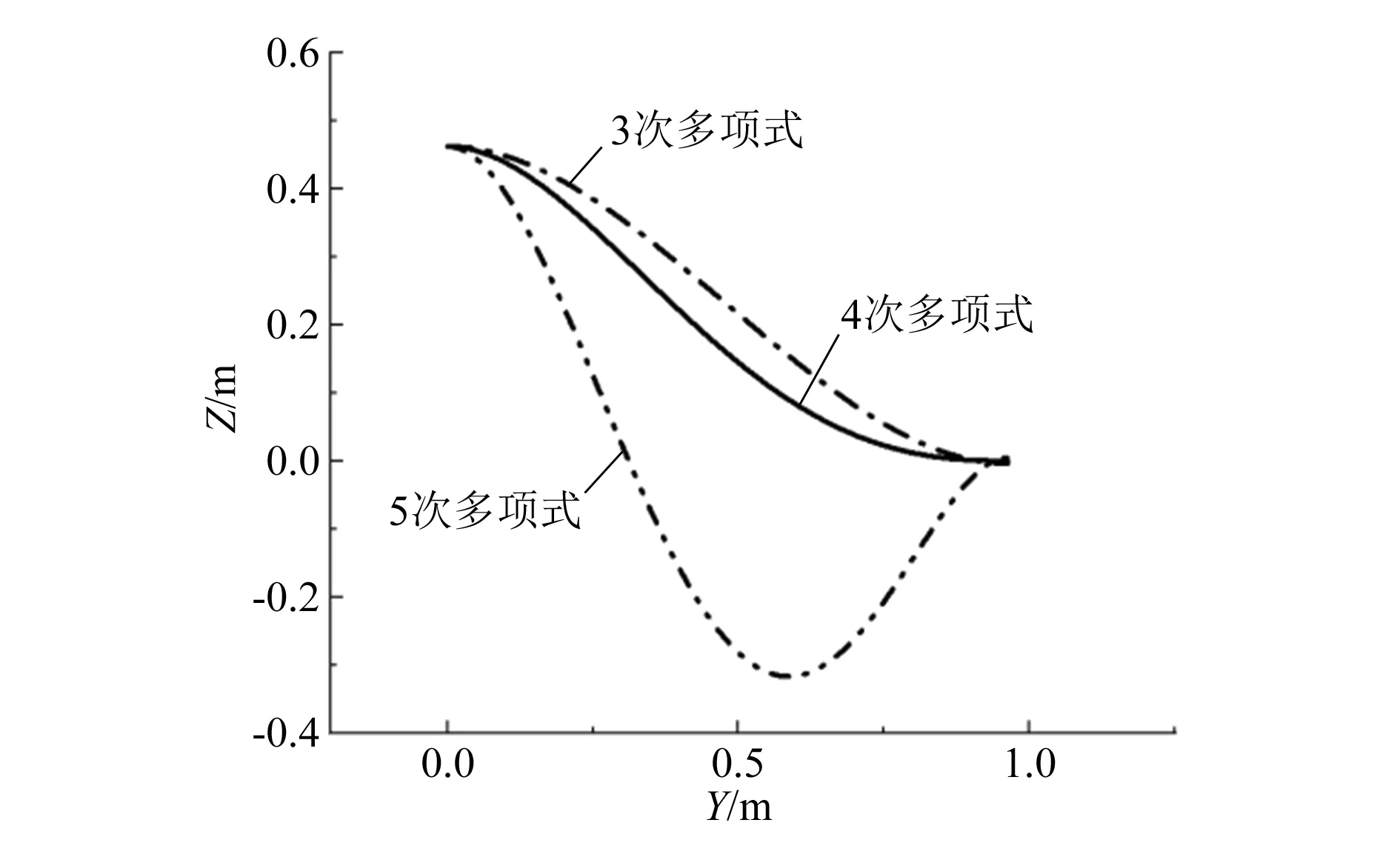
图2 优化后管簧轴线

表2所示为各函数的表达式以及吸收的能量，结合图2和表2可知，取5次多项式时，函数曲线出现强烈的震荡现象，故选取4次多项式作为起落架的外形函数。

表2 优化结果

将选取的4次多项式曲线导入CATIA中，画出管簧三维模型。选取6150M高强度弹簧钢作为起落架的制作材料，其屈服强度为1 490 MPa，密度为7 850 kg/m3，则优化后管簧的质量为11.2 kg。优化前管簧的质量为11.5 kg，质量减轻了2.7%。

4 起落架着陆仿真分析

本文采用有限元软件ABAQUS对起落架着陆过程进行仿真分析。ABAQUS软件隐式求解器和显式求解器的分析功能，适用于求解各种静力学、动力学等线性、非线性问题，广泛应用于航空航天、汽车工业等领域[11]。首先，通过建模软件对起落架部件建立三维模型，建模部件包括夹具、衬套、起落架管簧、轮辋、轴承、轮胎以及紧固件。其中轮胎结构较为复杂，包括束带层、连带层以及胎体等。对起落架着陆仿真前，需要先确定有效投放质量W，其与起落架垂向位移dLG有关。由于无法事先确定起落架的垂向位移dLG，需要通过试凑的方法确定投放质量W[6]。设计飞机最大着陆质量为1 080 kg，对于飞机最大着陆设计质量，使用下沉速度vz=1.8 m/s[1]对单个起落架着陆仿真，分别以335,355,365,385 kg为投放质量，用仿真得到的起落架垂向位移dLG计算有效投放质量W，确定投放质量为355 kg时符合要求。

本文研究重点在于起落架的着陆性能。为简化模型，节省计算成本，将轮辋、轴承、地面简化为刚体。飞机对称着陆时，投放质量采用上面的仿真结果，以集中质量点的形式耦合在夹具上表面；轴承内外圈采用多点约束，释放其转动自由度。采用动力显式分析方法，以1.8 m/s的速度着陆，时间步设置为0.2 s，将优化前与优化后起落架模型分别提交ABAQUS计算。图3、图4分别是起落架优化前、后的应力云图。

图3 起落架优化前应力云图

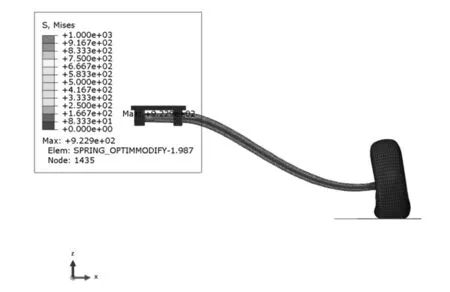
图4 起落架优化后应力云图

图3、图4中应力为高斯积分点应力，最大值均发生在与夹具相连部分，优化后起落架最大应力为922.9 MPa，与优化前的应力相比降低了6.2%。从图5、图6中可以看出，优化后起落架的垂向位移变大且峰值靠后，使飞机拥有更多的缓冲时间，同时起落架最大过载系数由2.5降到2.4。图7为起落架优化前、后吸能对比图，通过计算得到管簧起落架优化前、后的比吸能[12]分别为71.8,78.2 kJ/(kg·m3)，吸能效果提高了8.9%。优化后的起落架在结构质量减轻的同时，降低了着陆时的最大应力和过载系数，并且提高了比吸能。

图5 起落架垂向位移-时间图

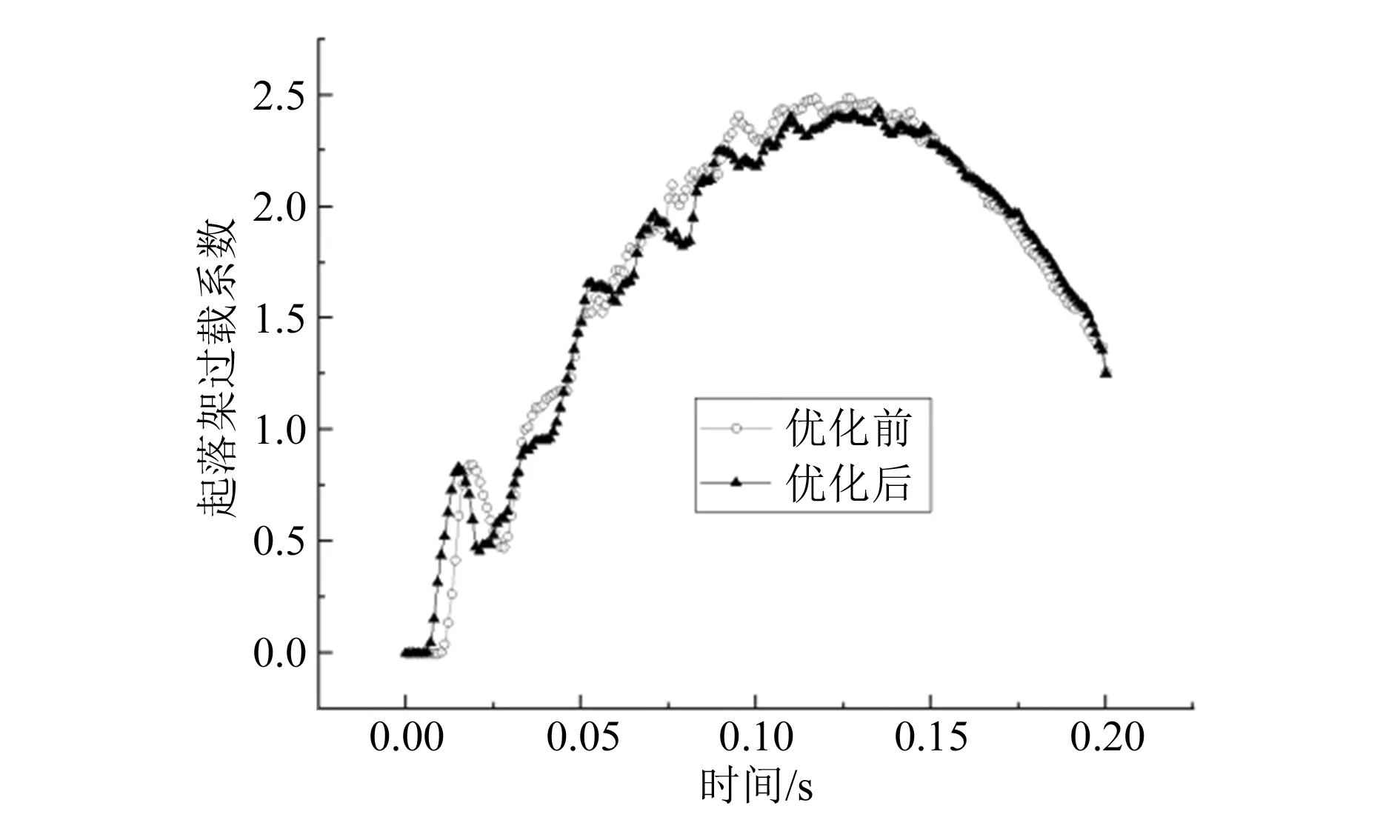
图6 起落架过载系数-时间关系图

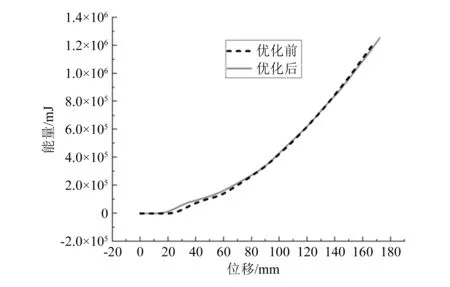
图7 起落架优化前、后吸能图

5 结论

本文针对弹簧式起落架缓冲吸能的特性，通过建立管簧式起落架的应变能吸收模型，优化了管簧的外形，并在ABAQUS中建立了飞机在落震过程中的动力学仿真模型，得到以下结论：

1)某型成熟的管簧式起落架仍有进一步的优化空间，优化后的起落架在减重的同时，还提高了起落架的着陆缓冲性能。

2)飞机着陆时的冲击能量转变为起落架管簧的应变能，改变管簧的外形能够直接影响管簧起落架的缓冲性能。

3)优化后的起落架能产生更大的形变，增加了管簧的柔性，减小了起落架所受的冲击载荷和过载系数，并且能吸收更多的冲击能量。该优化方法对弹簧式起落架的初步设计具有一定指导意义。