双边自由贸易协定对双边外商直接投资的影响机制——基于知识资本模型的分析

王效云

（中国社会科学院 俄罗斯东欧中亚研究所， 北京 100007）

一、问题提出

对外开放、 积极融入世界市场是中国经济获得高速发展的重要原因之一。 经过多年的发展， 中国已成为全球第二大消费市场、 第一大货物贸易国、 第一大对外投资国和第二大外资流入国。 当前正值两个一百年交汇的历史时期， 中国面临将贸易大国打造成贸易强国的历史使命。 党的十九大报告指出， 要“推动形成全面开放新格局……推进贸易强国建设”。 2021 年公布的《中华人民共和国国民经济和社会发展第十四个五年规划和2035 年远景目标纲要》 将“更高水平开放型经济新体制基本形成” 作为十四五时期经济社会发展主要目标之一， 明确提出要“深化经贸投资务实合作” “扩大双向贸易和投资” “实施自由贸易区提升战略， 构建面向全球的高标准自由贸易区网络……推动商签更多高标准自由贸易协定和区域贸易协定”。 可见， 引进外资、 推动对外投资以及构建高标准自由贸易区网络是中国近期对外经济合作的重要方向。

建立自由贸易区会影响成员国之间的资本流动， 但鉴于对其中的影响机制和作用渠道尚未完全厘清，学术界对于自由贸易协定（FTA） 究竟会促进还是阻碍成员国外商直接投资（FDI） 流入一直未能形成共识。 这意味着中国对外经济合作的目标之间可能存在一定的冲突和矛盾。 因此， 厘清FTA 与FDI 的关系，探明区域经济一体化协议影响成员国引进外资和对外直接投资的关键机制和渠道， 发现FTA 促进或阻碍成员国引进外资和对外直接投资的边界和条件， 不仅对国际经济学科本身具有重要的理论意义， 对构建中国对外开放新格局也具有重要的现实意义。

二、文献综述

从整体上研究区域经济一体化对FDI 影响的早期理论基于贸易和资本的替代假说， 认为签署FTA 可能会抑制一国FDI 的流入。 随着生产垂直分工和国际生产网络的发展， 贸易和投资的关系变得更加复杂，学者们对FTA 对成员国FDI 的影响也有了多样化的看法。

已有学者研究指出， 区域经济一体化会促进成员国的外资流入， 但对成员国外资流入的影响力度具有不对称性， 会随着成员国经济环境、 区位优势等因素而异［1-2］。 张勇俊（Jang， 2011） 指出， 考虑到区域经济一体化协议对成员国外资流入影响的不对称性， 将双边FDI 和多边FTA 进行回归， 以此判断FTA对成员国FDI 的影响方向是不严谨的， 因此将视角缩小到双边FTA 和双边FDI 之间［3］。 基于跨国投资的知识资本模型， 他进一步将跨国投资划分为两种类型： 技术水平差距大的发达国家和发展中国家之间的双边FDI （南北型FDI）， 以及技术水平差距小的发达国家之间的双边FDI （北北型FDI）。 其中， 南北型FDI 以垂直型FDI 为主， 与贸易存在相互促进的关系； 北北型FDI 以水平型FDI 为主， 与贸易存在相互替代的关系。 考虑到FTA 将带来成员国之间双边贸易成本的下降从而促进双边贸易， 他提出假设： 发达国家和发展中国家之间的南北型FTA 将促进双边FDI， 而发达国家之间的北北型FTA 将抑制双边FDI。 小山田（Oyamada， 2017） 利用修正的知识资本模型探讨发达国家和发展中国家之间签署的区域经济一体化协议对发展中国家FDI 流入的影响［4］， 他的研究结论支持张勇俊的假设。

另有一些学者将研究视角锁定在具体的区域经济一体化协定对成员国FDI 的影响方面。 部分学者认为区域一体化协定促进了双边投资。 林淑君等（Lim et al.， 2020） 研究东盟-韩国自由贸易区对于韩国对东盟国家FDI 的影响， 发现韩国和东盟之间的投资和贸易主要呈现互补关系， 东盟-韩国FTA 对于这一互补关系具有一定的调节作用， 东盟-韩国一体化协议的实施不仅促进了双边贸易， 也促进了双边投资［5］。 奥克塔维和韦里科（Oktavia ＆ Verico， 2020） 研究东盟创建的经济一体化组织， 包括东盟自由贸易区（AFTA）、 AFTA+1 和东盟经济共同体（AEC） 对于东盟内部贸易和FDI 的影响， 认为东盟+框架会在东盟和伙伴国家创造投资［6］。 部分学者认为FTA 能否促进FDI 是不确定的， 取决于诸多因素的影响。 谢里夫和德雷格 （Cherif ＆ Dreger， 2018） 研究阿加迪尔、 南方共同市场（MERCOSUR） 和东盟自由贸易区（AFTA） 协定对跨国公司FDI 决策的影响， 认为经济一体化协议能否促进FDI 流入， 受诸多因素影响［7］。对于商业友好的东道国来说， 对外贸易和金融市场的开放对于吸引FDI 而言是最重要的两大因素。 还有一部分学者侧重于分析FTA 影响FDI 的渠道和机制。 有学者使用创新的可计算一般均衡（CGE） 模型研究区域全面经济伙伴关系协定（RCEP） 对中国FDI 流入的潜在影响， 认为RCEP 对投资的影响主要有两个途径， 一是直接带来的投资自由化， 二是通过贸易自由化间接影响投资， 结果显示RCEP 将通过上述两种途径显著增加中国的FDI 流入［8］。 李乔敏和马阿尼（Li ＆ Maani， 2018） 以中国-东盟自由贸易协定（ACFTA） 为案例， 检验FTA 促进FDI 的两种效应： 市场扩张效应和垂直分割效应， 发现ACFTA 存在促进上述两种效应， 其中市场扩张效应可以帮助具有国际竞争力的部门吸引更多寻求市场的FDI， 而垂直分割效应可以促进垂直FDI 流向中间产品贸易密集的部门［9］。

国内学者对区域经济一体化投资效应的研究相对较少。 仅有的几篇文献大都以中国为研究对象， 研究中国加入的区域一体化协议对成员国引进外资和对外投资的影响， 例如郎永峰（2010）、 姜庆默（2015） 分别研究中国-东盟FTA （CAFTA） 和中韩FTA 对成员国的投资效应［10-11］， 董有德和赵星星（2014）、 孙玉红和许智贤（2018） 基于跨国公司知识资本模型研究加入区域经济一体化对中国企业对外直接投资的影响［12-13］。

综上， 由于区域经济一体化对成员国FDI 的影响问题在理论上没有取得一致认识， 因而更多地被作为一个实证问题来研究， 而实证研究结论则随着样本的差异而不同。 对于实证研究来说， 从样本的选择上基本可以分为两类： 第一类是针对多国的、 不明确具体区域经济一体化协议的大样本分析， 第二类是以某一个或几个具体的区域经济一体化协议为案例的具体分析。 然而， 对于多国大样本数据分析来说， 将双边FDI 和多边FTA 进行回归， 以此判断FTA 对成员国FDI 的影响方向是不严谨的［3］； 而对于具体案例的样本分析来说， 研究结论不足以反映内在规律的普遍性和客观性。 更为关键的问题在于， 大多数的实证分析都停留在数据分析上， 缺少对区域经济一体化协议影响FDI 机理的理论探讨， 而区域经济一体化影响FDI 的机制和渠道， 才是实证研究更重要的意义所在。

本文的分析是在张勇俊（2011）［3］的研究基础上的进一步拓展。 本文认为， 尽管张勇俊基于跨国投资的知识资本模型对跨国投资类型进行划分具有重要意义， 但基于FTA 通过贸易成本效应影响FDI 而提出上述假设仍是不严谨的， 原因在于FTA 对双边FDI 的影响不止贸易成本一条途径。 近年来， 越来越多的FTA 都包含投资条款， 将削减投资壁垒、 促进投资自由化和便利化纳入区域经济合作目标， 而投资条款将直接作用于东道国投资环境， 从而有利于促进外资流入。 此外， 长期来看， FTA 对一国经济增长也具有促进效应， 而经济规模越大， 越有利于外资的流入。 因此， 衡量FTA 对双边FDI 的影响， 需要综合考虑贸易成本、 投资规则、 经济规模等诸多因素。

本文的边际贡献在于： 一是从影响FDI 的因素入手， 分析FTA 可能作用于FDI 的渠道和机制， 在跨国直接投资的知识资本模型下， 建立双边FTA 影响双边FDI 的完整分析框架； 二是将发展中国家之间签署的南南型FTA 对FDI 的影响情况纳入实证分析模型， 补充完善样本类型。

三、机制分析和假设提出

（一） 机制分析

FTA 对FDI 的影响机制十分复杂。 一方面， FTA 本身具有很大的差异性， 主要表现为： 一是在协议内容上， 有的FTA 包含投资条款， 涉及消除投资壁垒、 促进投资自由化的内容； 而有的仅包含贸易条款。二是在协议的执行上， 不同缔约国之间对FTA 的执行力度差异很大， 有的国家虽然签署了含有投资条款的FTA， 但却不能有效实施， 未能充分发挥应有的作用。 另一方面， FDI 自身也具有很强的异质性。 从跨国投资的动机出发， 目前学术界倾向于将FDI 分为两类： 垂直型FDI （vertical FDI）［14-15］和水平型FDI （horizontal FDI）［16-17］。 鉴于国家层面的FDI 数据难以区分， 已有学者提出了知识-资本模型（knowledgecapital model）， 将垂直型FDI 和水平型FDI 纳入统一的分析框架中［17-19］。 不同类型的FDI 有其不同的影响因素， 对FTA 的反应机制差异很大。 为厘清双边FTA 影响双边FDI 的机制和渠道， 本文将从东道国吸引外资流入的角度出发， 借助跨国直接投资的知识资本模型， 探究FTA 对FDI 发挥作用的渠道和机制。

1.FDI 的影响因素

第一， 影响水平型FDI 的核心要素是市场规模和贸易成本。 马库森（Markusen， 1984） 基于企业规模经济， 提出了跨国直接投资的水平型动机［16］。 水平型FDI 的特征是跨国公司在多个国家生产相同的产品，通过海外生产来供给海外市场。 对于供给海外市场而言， 跨国公司有两种方式可供选择， 即出口和水平型FDI。 如果企业通过FDI 的方式供给海外市场， 将损失在母国集中生产的规模经济收益， 同时还需面临在海外设厂的固定成本支出， 但可以节省关税、 非关税壁垒、 运输成本等贸易成本支出， 因此水平型FDI通常被称为跨国公司的关税跳跃（tariff-jumping） 战略。 如果企业将生产集中在母国完成， 然后通过出口将产品供给海外市场， 则企业可以享受因集中生产带来的规模经济收益， 但需要面临关税等贸易成本损失。 因此， 在供给海外市场时， 跨国公司面临着规模经济和关税跳跃之间的权衡［20］。 当两国之间的关税等贸易成本下降时， 通过出口供给海外市场将更为有利， 跨国公司将减少在东道国的投资， 贸易成本和水平型FDI 呈正相关关系， 即贸易成本越低， 水平型FDI 越低。

此外， 伊拉拉萨巴尔等（Irarrazabal et al.， 2009） 指出， 在水平型FDI 中， 还存在着跨国公司总部向海外分支机构出口核心零部件的公司内贸易， 如此水平型FDI 本身也受贸易成本的影响［21］。 如果贸易成本下降， 跨国公司从总部向海外分支机构出口核心部件等中间品的成本则会下降， 从而推动降低跨国公司海外生产总成本， 由此可能激励跨国公司增加海外投资。 但总体而言， 贸易成本和水平型FDI之间仍然呈正向关系， 即水平型FDI 随贸易成本的下降而降低。

第二， 影响垂直型FDI 的核心要素是贸易成本、 要素禀赋和技术差距。 水平型FDI 的出发点是供给海外市场， 而垂直型FDI 的出发点则是在全球范围内分割生产、 配置生产要素以提高生产效率。 格里纳韦和克内勒（Greenaway ＆ Kneller， 2007） 定义水平型FDI 是市场寻求型（market-seeking）， 而垂直型FDI 是要素寻求型（factor-seeking）［22］。 垂直型FDI 最早由赫尔普曼（Helpman， 1984）［14］在规模经济和不完全竞争的一般均衡贸易框架下提出， 赫尔普曼和克鲁格曼（Helpman ＆ Krugman， 1985）［15］对其进行了扩展。在垂直型FDI 中， 跨国公司为追求生产效率， 将非熟练劳动力（un-skilled labor） 密集型的生产活动安排在非熟练劳动力相对丰裕的地区（通常是东道国）， 而将熟练劳动力（skilled labor） 密集型的生产活动安排在熟练劳动力相对丰裕的地区（通常是母国）。 跨国公司将生产的核心部件（中间品） 从在母国的总部出口到在东道国的生产工厂， 当在东道国完成生产后， 跨国公司再将最终产品进口到母国， 供应母国市场。

要素禀赋和技术差距是垂直型FDI 存在的前提条件。 当两国之间的要素禀赋和技术差距足够大时，跨国公司将生产按照要素使用密集度的不同在两国之间进行分割才有利可图， 此时垂直型FDI 才可能产生。 贸易成本是影响垂直型FDI 的重要因素。 当两国之间的贸易成本下降时， 跨国公司出口中间产品、 进口最终产品的成本降低， 由此将激励跨国公司增加投资， 即贸易成本与垂直型FDI 之间呈负向关系。

2. 双边FTA 影响双边FDI 的机制分析

FTA 旨在通过削减贸易和投资壁垒， 促进伙伴国之间贸易和跨境投资的自由化和便利化。 贸易规则和投资规则是FTA 的核心要素。 在FDI 的诸多影响因素中， 有三种因素直接与FTA 有关。 一是贸易成本，即FTA 的贸易规则将降低伙伴国之间的贸易成本， 以此将对不同类型的双边FDI 产生相应的影响。 二是投资制度环境， 随着区域一体化向纵深发展， 越来越多的FTA 包含有投资、 竞争、 知识产权等条款， 特别是投资条款的覆盖面很广， 这些条款旨在改善东道国投资环境， 促进伙伴国之间的投资。 三是市场规模， FTA 还将通过促进成员国经济发展带来市场规模的扩大， 进而间接促进双边FDI。 因而， 双边FTA 影响双边FDI 的机制主要包括如下几个方面：

第一， 贸易成本效应。 FTA 的贸易规则包括关税和非贸易壁垒等内容， 其核心在于削减有形和无形的贸易壁垒， 降低贸易成本， 以促进双边贸易的发展。 FTA 的贸易成本效应指FTA 成立带来双边贸易成本的降低， 以此对双边FDI 产生的效应。 通过贸易成本效应影响双边FDI 较投资规则机制复杂得多， 取决于双边FDI 的类型。 结合上文对FDI 影响因素的分析可知， 通过FTA 降低双边贸易成本， 将抑制水平型FDI、 促进垂直型FDI 的发展。 下面将在跨国投资的知识资本模型框架下， 对此做进一步探讨。

跨国投资的知识资本模型基于三个基本假设： 一是基于知识的服务和活动（例如研发） 可以从生产中分离出来， 并以很低的成本提供给生产部门。 二是知识密集型的活动相对于其他生产活动而言是熟练劳动力密集型的。 三是基于知识的服务有联合投入（joint-input） 的特质， 可以在多个生产基地同时被使用。 前两个假设给企业提供了将生产进行垂直分割的动机， 将研发等知识密集型的活动安排在熟练劳动力价格相对便宜的地区进行， 而将生产组装等非熟练劳动密集型的活动安排在非熟练劳动力价格相对便宜的地区。 第三个假设意味着企业生产具有规模经济， 给企业提供了将同样的生产和服务在多个地区复制的水平型投资动机。 根据知识资本模型， 当两国之间的要素禀赋和技术差距水平相差较大时， 企业在两国间进行垂直型投资的动机较强， 两国投资将以垂直型FDI 为主。 当两国之间要素禀赋和技术水平相差不大时， 企业进行水平型投资的动机较强， 两国投资以水平型FDI 为主。 这意味着， 在知识资本模型下，贸易成本对FDI 的影响方向与两国之间要素禀赋和技术差距有关。 对此， 卡尔等（Carr et al.， 2001） 指出贸易成本对FDI 的影响取决于国家之间要素禀赋的差异性［23］。 当两国之间要素禀赋差异很小时， 双边水平型FDI 的激励增加， 双边FDI 随着贸易成本的降低而降低； 当两国之间要素禀赋差距差异很大时， 双边垂直型FDI 的激励增加， 双边FDI 随着贸易成本的降低而增加。 不少学者也得出类似的结论［3，24］。 由此， FTA 通过贸易成本效应影响双边FDI 取决于两国之间的要素禀赋和技术差距。 当两国之间要素禀赋和技术差距较大时， 双边FDI 以垂直型FDI 为主， FTA 通过降低贸易成本促进双边FDI； 当两国之间要素禀赋和技术差距较小时， 双边FDI 以水平型FDI 为主， FTA 通过降低贸易成本抑制双边FDI。

第二， 投资规则效应。 FTA 通过投资规则优化伙伴国投资制度环境， 进而促进双边FDI。 这集中体现在FTA 的投资条款中。 FTA 的投资规则一般涉及投资范围（包括投资和投资者定义）、 投资待遇（包括国民待遇、 最惠国待遇、 最低标准待遇等）、 投资保护（包括征收和补偿、 损失和补偿、 转移、 业绩要求、高管和董事会成员、 代位权等）、 东道国义务豁免以及争端解决。 新一代FTA 还涉及竞争政策、 知识产权、 政府采购等内容， 旨在降低对外国投资者的限制， 营造公平竞争的良好市场环境， 促进双边跨国投资的发展。 但不同的FTA 投资规则具有很大的差异性， 对FDI 的影响力度也十分不同。 例如在范围方面，有的FTA 约定仅适用于个别行业， 采用正面清单的方式， 有的则适用于大部分行业， 采用负面清单的方式； 在投资者待遇方面， 有的FTA 仅限于准入后的待遇， 有的则将国民待遇等延伸到准入前阶段； 在争端解决方面， 有的FTA 仅停留在纸面上， 有的则建立了明确可行的争端解决机制。 此外， 在FTA 生效后，不同缔约国对FTA 的执行力度也具有很大的差异性。

第三， 市场规模效应。 FTA 的市场规模效应主要源于两方面： 一是FTA 在成员国之间建立了一个相对统一的大市场， 直接扩大了市场规模； 二是FTA 的成立将有助于促进成员国经济增长， 长期来看， 以国内生产总值（GDP） 表示的市场规模得以扩大。 FTA 通过促进成员国经济增长扩大市场规模， 进而有助于提高双边FDI 的流入。 市场规模效应对于吸引区域外投资比较明显， 本文的市场规模效应主要指第二方面。 但FTA 本身能否促进成员国经济增长尚需谨慎论证。 对于伙伴国之间的FDI 流入而言， 市场规模效应远小于贸易成本效应和投资规则效应， 且是一种长期效应。

（二） 假设提出

FTA 同时通过上述三种效应影响伙伴国之间双边FDI 的流入， 将三种影响叠加考虑， 可以得出如下结论：

第一， 对水平型FDI 而言， FTA 通过投资规则效应和市场规模效应促进双边FDI 流入， 通过贸易成本效应抑制双边FDI 流入。 FTA 对水平型FDI 的综合影响方向是不确定的， 取决于三者力量的较量。

第二， 对垂直型FDI 而言， FTA 通过投资效应、 贸易成本效应和市场规模效应促进成员国间FDI 流入。 FTA 对垂直型FDI 的综合影响方向是明确的， 即FTA 将促进双边垂直型FDI 的流入。

在知识-资本模型框架下， 本文提出如下假设：

假设H1： 对于发达国家和发展中国家之间成立的FTA 而言（南北型， NS 型）， 双方要素禀赋和技术差距显著， 双边FDI 以垂直型FDI 为主， FTA 的成立将促进双边FDI 的流入。

假设H2： 对于发达国家之间成立的FTA 而言（北北型， NN 型）， 双方要素禀赋和技术差距较小， 双边FDI 以水平型FDI 为主， FTA 对双边FDI 的最终影响方向不确定， 取决于正的投资规则效应和市场规模效应与负的贸易成本效应之间的角逐。

假设H3： 对于发展中国家之间成立的FTA 而言（南南型， SS 型）， 双方要素禀赋和技术差距较小，双边FDI 以水平型FDI 为主， FTA 的成立对双边FDI 的最终影响方向不确定， 也可因各种效应之间的作用互相抵消， 最终影响并不显著。

双边FTA 对双边FDI 影响机制框架如图1 所示。

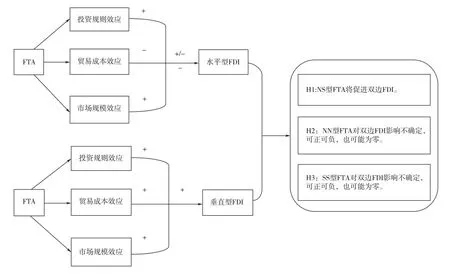
图1 双边FTA 对双边FDI 影响机制框架

四、实证分析

为验证上述推论， 本文将建立回归模型进行实证检验。 本文将样本划分为四组： 发达国家组（NN 样本组）、 发达国家和发展中国家组（NS 样本组）、 发展中国家组（SS 样本组）， 以及上述所有样本组（ALL 样本组）。 根据上文理论分析， NS 样本组的FDI 以垂直型FDI 为主， NN 样本组和SS 样本组的FDI以水平型FDI 为主。 下面将建立回归模型， 实证检验各样本组的FTA 对双边FDI 的影响。

（一） 回归模型及变量解释

卡尔等（2001） 实证分析了经济规模、 技术差距、 贸易成本和投资成本， 以及交互项对知识-资本模型下FDI 的影响［23］。 埃格和普法弗迈尔（Egger ＆ Pfaffermayr， 2004） 在此基础上加入了双边投资条约作为解释变量， 发现双边投资条约与双边FDI 之间存在显著的正向关系［24］。 张勇俊（2011） 进一步加入了FTA 虚拟变量、 FTA 与技术差距和双边距离的交互项、 对外开放度等解释变量［3］。 裴灿权和张勇俊（Bae＆ Jang， 2013） 将回归模型进行精简， 去掉了交互项， 并将要素禀赋差异纳入模型中［20］。 本文在已有的回归模型基础上， 加入东道国法治程度、 语言等解释变量。 回归模型设定如下：

lnFDIijt=β0+β1lnGDPijt+β2SIMIijt+β3ΔSKijt+β4FTAijt+β5BITijt+β6lnDISijt+β7LANijt+β8RULijt+

β9FTAijt×ΔSKijt+β10FTAijt×lnDISijt+β11ΔSKijt×lnGDPijt+β12ΔSKijt×lnDISijt+μijt+τijt+εijt（1）

其中，i、j和t分别代指母国、 东道国和年份。μijt、τijt和εijt分别代表国家组固定效应、 时间固定效应以及误差项。

1. 被解释变量

FDIijt是被解释变量， 指第t年东道国j从母国i引进的FDI 流量。

2. 解释变量

FTAijt是本模型的关键解释变量， 当FTA 生效之后取值为1， 否则为0。 根据理论假设， 在NS 样本组中， 双边FDI 以垂直型FDI 为主， FTA 对双边FDI 起促进作用， 回归系数为正（β4＞0）。 在NN 样本组和SS 样本组中， 双边FDI 以水平型为主， FTA 对FDI 的影响方向不确定。 对于ALL 样本组而言， FTA 对FDI 的影响受各方因素的综合影响， 也是不确定的。

FTAijt×ΔSKijt是FTA 和技术差距（要素禀赋差异） 的交互项， 用来考察FTA 对双边FDI 的影响是否会随着两国要素禀赋的差异性而不同。 已有研究表明， 成员国之间的要素禀赋和技术差距越大， FTA 对垂直型FDI 的影响越显著［2］。 本文预计在NS 样本组和ALL 样本组中，FTAij×ΔSKijt对FDI 起促进作用， 回归系数为正（β9＞0）， 在SS 样本组和NN 样本组中则不显著。

FTAijt×lnDISijt是FTA 和经济规模相似度以及两国距离的交互项。 FTA 对垂直型FDI 其促进作用， 对水平型FDI 作用方向不确定， 距离作为贸易成本的一部分， 会促进水平型FDI， 抑制垂直型FDI。 因此， 预计在NS 样本组中，FTAijt×lnDISijt将抑制双边FDI， 回归系数为负（β10＜0）； 在NN 样本组、 SS 样本组和ALL 样本组中， 影响方向不确定。

3. 控制变量

GDPijt是市场规模的代理变量。GDPijt=GDPit+GDPjt。 根据上文的分析， 市场规模扩大将促进FDI 流入， 因此预计四个样本组的FDI 都将随着GDPijt的提高而增加， 回归系数为正（β1＞0）。

SIMIijt指两 国 经 济 规 模 的 相 似 性。SIMIijt= 1- ［GDPit／（GDPit+GDPjt） ］2- ［GDPjt／（GDPit+GDPjt） ］2。 该指数越大， 代表两国经济规模相似度越高。 卡尔等（2001） 认为跨国子公司的产量与母国和东道国经济规模的差距之间存在倒U 型关系， 并发现经济规模差距对跨国投资的抑制作用［23］。 学者们进一步用经济规模的相似性指数替代经济规模差距指标， 实证发现了经济规模相似性与FDI 之间存在正向关系［3，20］。 基于上述研究， 本文预计SIMIijt对四个样本组的FDI 均起促进作用， 回归系数为正（β2＞0）。

ΔSKijt是两国之间技术差距的代理指标。 ΔSKijt=│lnpercapGDPit-lnpercapGDPjt│。 其中，percapGDPi／jt分别代表i国和j国t年的人均GDP。 根据理论假设， 两国技术差距将对垂直型FDI 起积极作用， 但不影响水平型FDI。 因此， 预计NN 样本组和SS 样本组的ΔSKijt回归系数不显著， NS 样本组和ALL 样本组的ΔSKijt回归系数为正（β3＞0）。

BITijt是虚拟变量， 代表双边投资协定。 当双边投资协定生效后， 取值为1， 否则为0。 两国之间签署并实施双边投资协定， 意味着降低双边投资壁垒， 优化投资制度环境， 有利于促进双边FDI 的流入。 因此， 预计四个样本组的BIT对双边FDI 都起促进作用， 回归系数为正（β5＞0）。

DISijt指两国之间的距离。 距离是构成贸易成本的重要因素， 即距离越远， 贸易成本越高。 距离与水平型FDI 呈正相关关系， 与垂直型FDI 呈负相关关系。 因此， 预计在NS 样本组中， 距离增加将抑制双边FDI， 回归系数为负（β5＜0）， 在NN 样本组和SS 样本组中， 距离增加将促进双边FDI， 回归系数为正（β6＞0）。 在ALL 样本组中， 距离对双边FDI 的影响方向不确定。

LANijt是语言虚拟变量。 如果两国之间有同一种官方语言， 或者各有超过9%的人口使用同一种语言，取值为1， 否则为0。 是否有共同的语言显著影响跨国沟通的效率。 此外， 共同的语言通常意味着双方的文化背景更为相似， 有助于企业更好地适应东道国市场环境， 将对双边FDI 起促进作用。 因此， 预计在四个样本组中， 回归系数均为正（β7＞0）。

RULijt是东道国制度环境的代理指标， 取自世界银行政府治理指数数据库全球治理指标（WGI） 三个指数之和， 分别是法治水平指数（rule of law）、 执政能力指数（regulatory quality） 以及言论自由和问责指数（voice and accountability）。 该指标综合体现了一国法律体系质量（反映合约执行质量、 产权保护、 警察和法院的公正效率、 社会治安等方面）、 政府制定和执行良好政策的能力， 以及公民社会的自由权利和活力。 该指数越高， 代表东道国的制度环境越好， 企业经营面临的环境更为透明， 市场机制更为有效，从而有助于吸引跨国投资流入。 因此， 预计该项指标的回归系数在四个样本组中均为正值（β8＞0）。

ΔSKijt×lnGDPijt是技术差距和市场规模的交互项。 技术差距影响垂直型FDI， 但不影响水平型FDI， 市场规模对垂直型FDI 和水平型FDI 都有促进作用， 因此预计该项变量对NS 样本组的双边FDI 起促进作用， 回归系数为正（β11＞0）； 对NN 样本组和SS 样本组的双边FDI 没有明显影响， 回归系数不显著； 对ALL 样本组的FDI 也将起促进作用， 回归系数为正。

ΔSKijt×lnDISijt是技术差距和距离的交互项。 技术差距对垂直型FDI 的影响将随着双边距离的增加而减弱， 预计在NS 样本组中， 该变量的回归系数为负（β12＜0）； 在NN 样本组和SS 样本组中， 回归系数不显著； 在ALL 样本组中， 回归系数为负（β12＜0）。

（二） 数据描述和预处理

综合参考世界银行（World Bank）、 联合国贸易和发展会议（UNCTAD）、 国际货币基金组织（IMF）1996—2017 年对发达国家和发展中国家的分类， 本文选取26 个发达国家①分别是： 澳大利亚、 日本、 韩国、 新加坡、 新西兰、 美国、 加拿大、 奥地利、 比利时、 塞浦路斯、 丹麦、 芬兰、 法国、 德国、 瑞典、 瑞士、 英国、 希腊、 西班牙、 冰岛、 爱尔兰、 意大利、 卢森堡、 荷兰、 挪威和葡萄牙。、 34 个发展中国家②分别是： 越南、 中国、 文莱、 柬埔寨、 印度、 印度尼西亚、 老挝、 缅甸、 马来西亚、 菲律宾、 哈萨克斯坦、 阿拉伯联合酋长国、土耳其、 波兰、 俄罗斯、 乌克兰、 克罗地亚、 匈牙利、 墨西哥、 尼加拉瓜、 巴拿马、 秘鲁、 乌拉圭、 智利、 阿根廷、 巴西、 哥伦比亚、 哥斯达黎加、 多米尼加、 厄瓜多尔、 洪都拉斯、 毛里求斯、 埃及和南非。作为考察对象。

将上述国家根据数据的可得性两两组合， 然后划分到四个样本组， 即可得发达国家之间的NN 样本组223 组， 发达国家与发展中国家之间的NS 样本组274 组， 以及发展中国家的SS 样本组109 组。 数据来源如表1 所示。

表1 数据来源

表2 报告了分组样本关键变量的描述性统计。 其中， 发达国家之间的双边FDI 均值（7.72） 远超过发达国家和发展中国家的双边FDI 均值（3.68）， 以及发展中国家之间的双边FDI 均值（2.49）。 发达国家和发展中国家之间的平均技术差距（15.28） 远超过发展中国家之间的平均技术差距（0.88），以及发达国家之间的平均技术差距（0.37）。 在经济规模相似性SIMI方面， 发达国家之间的经济规模相似性最高（0.28）， 其次为发展中国家之间（0.23）， 发达国家和发展中国家之间的经济规模相似性最低（0.22）。 在市场规模指标lnGDP方面， 发达国家之间的平均市场规模最大， 为28.63， 其次为发达国家和发展中国家之间， 发展中国家之间最低。 在东道国制度环境RUL方面， NN 样本组的平均值为4.57， 远超过NS 样本组（-0.99） 和SS 样本组（-1.17）， 说明发达国家的制度环境和政治稳定性远远好于发展中国家， 与现实状况一致。

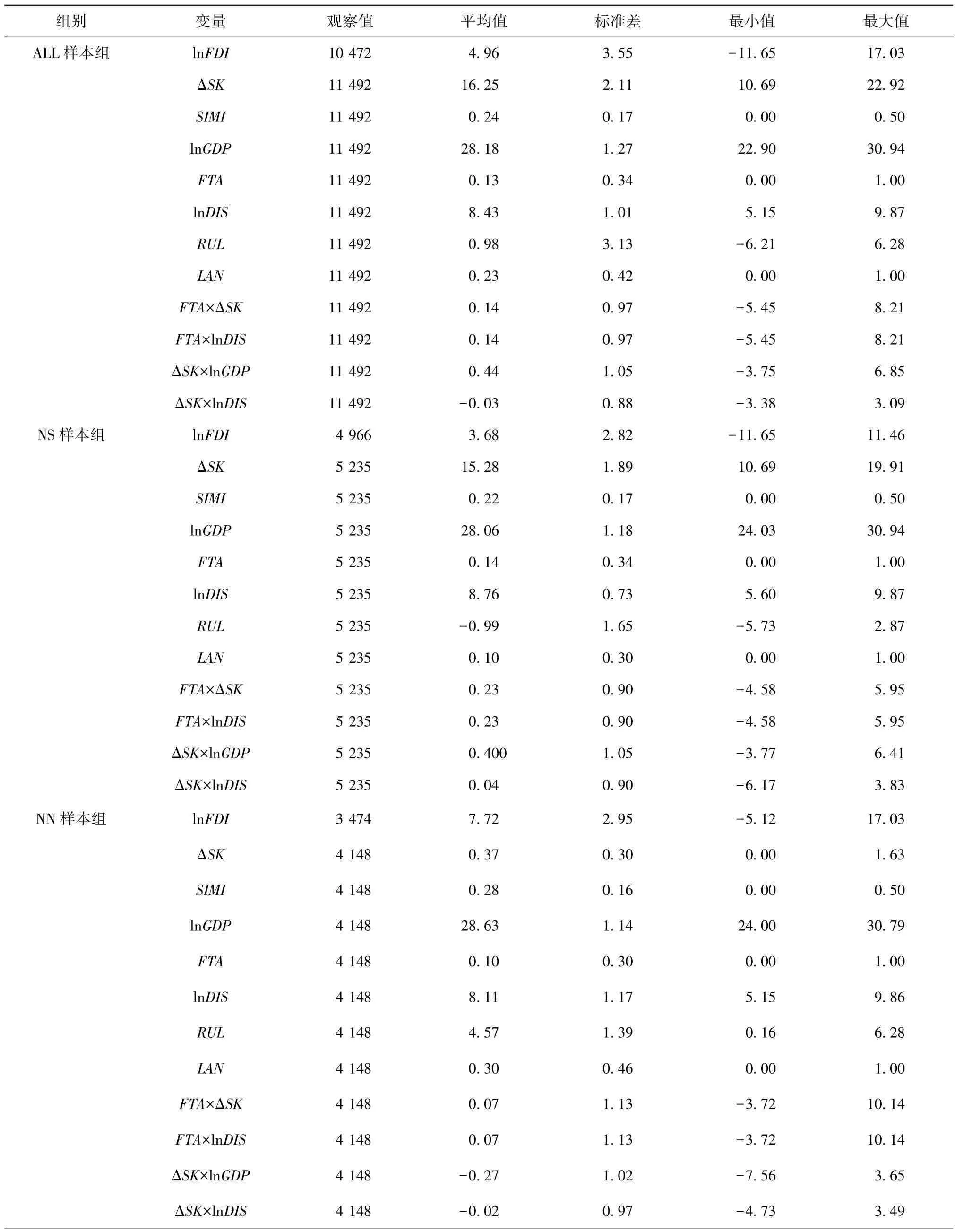
表2 关键解释变量的描述性统计

表2（续）

（三） 回归分析

1. 估计方法

本文所采用的数据是1996—2017 年， 包含断点的非平衡面板数据。 样本数据均为N＞T的短面板数据。 在估计方法的选择中， 首先， 需要检验是否存在个体效应， 即在固定效应模型和混合普通最小二乘法（OLS） 之间， 以及随机效应模型和混合OLS 之间做选择。 如果存在个体效应， 用固定效应模型或随机效应模型估计更有效［25］。 其次， 如果模型存在个体效应， 检验解释变量与个体效应是否相关。 如果解释变量与个体效应不相关， 则用随机效应模型估计比固定效应模型估计更有效。 第三， 检验时间效应的显著性， 如果时间效应显著， 则模型设定为双向固定效应模型更为有效。

在进行检验时， 首先， 通过F 检验发现固定效应模型优于混合OLS。 其次， 通过布伦斯-帕甘（BP） 检验发现随机效应模型优于混合OLS。 第三， 通过豪斯曼（Hausman） 检验， 发现解释变量与个体效应无关的随机效应模型前提假设条件不满足， 故应选择固定效应模型估计。 第四， 通过沃尔德（Wald）检验测度时间的显著性， 发现所有样本均存在显著的时间效应。 然而， 在实际回归中， 加入时间效应对关键解释变量的影响很小， 模型整体拟合优度的改善也不大， 但因时间序列较长加入时间变量模型将损失较多的自由度， 因此最终回归时选择不带时间效应的单向固定效应模型。

2. 估计结果分析

表3 汇报了在聚类稳健标准误下的固定效应模型估计结果。 每组样本回归结果分为Lag （0） —Lag （3）四种， Lag （0） 表示回归中使用的是解释变量的水平值（当期值）， Lag （1） —Lag （3） 分别表示除了其他变量仍然使用水平值之外，FTA和BIT均采用的是滞后1—3 期值。 之所以将滞后项作为解释变量纳入模型进行回归， 是为了检验FTA 的时间效应。 FTA 作为政策变量， 对实际经济和市场环境的影响需要一定时间才能显现。 FTA 通过贸易效应、 投资规则效应以及市场规模效应传导到跨国公司投资决策部门有一定的时滞， 跨国公司从决定投资到实施投资之间往往也有一定的时滞， 因此从理论上来说，FTA 的滞后项比水平值对FDI 的影响可能更显著。

从回归结果看， NS 样本组中，FTA的回归系数均为正， 但仅有滞后1 期的回归系数在5%的水平上显著， 说明发达国家和发展中国家之间的双边FTA 对于促进双边FDI 具有积极意义， 而且FTA 对双边FDI发生作用需要一年的时间， 即FTA 在实施一年后开始显著促进双边FDI 的流入。 FTA 与技术差距的交互项回归系数统计上不显著， 但与距离的交互项系数为负且统计上显著， 说明发达国家和发展中国家之间相距越近， 双边FTA 越能促进FDI。

NN 样本组和SS 样本组中， FTA 的回归系数统计上均不显著， 意味着在样本范围内， 发达国家之间和发展中国家之间的双边FTA 对双边FDI 的流入都没有明显影响。 该结果与张勇俊 （2011）［3］的研究结论不一致。 原因在于： 本文的样本期为1996—2017 年， 晚于张勇俊 （2011）［3］的研究样本期（1982—2005 年）， 这一时期区域经济一体化向纵深发展， 很多FTA 中都包含了投资条款。 回归结果说明对FDI 起促进作用的投资规则效应和市场规模效应， 与起抑制作用的贸易成本效应基本抵消， 使得FTA 对FDI 的最终影响并不显著。

当把发达国家之间、 发展中国家之间， 以及发达国家和发展中国家之间的样本统一分析时， 发现双边FTA 当期值的回归系数为正且在10%的水平上显著， FTA 滞后1—3 期的回归系数也均为正， 但统计上不显著。 结合上述三种样本类型中FTA 对FDI 的各不相同的影响方向， 可知这样的检验结果是合理的。

表3 固定效应模型回归结果

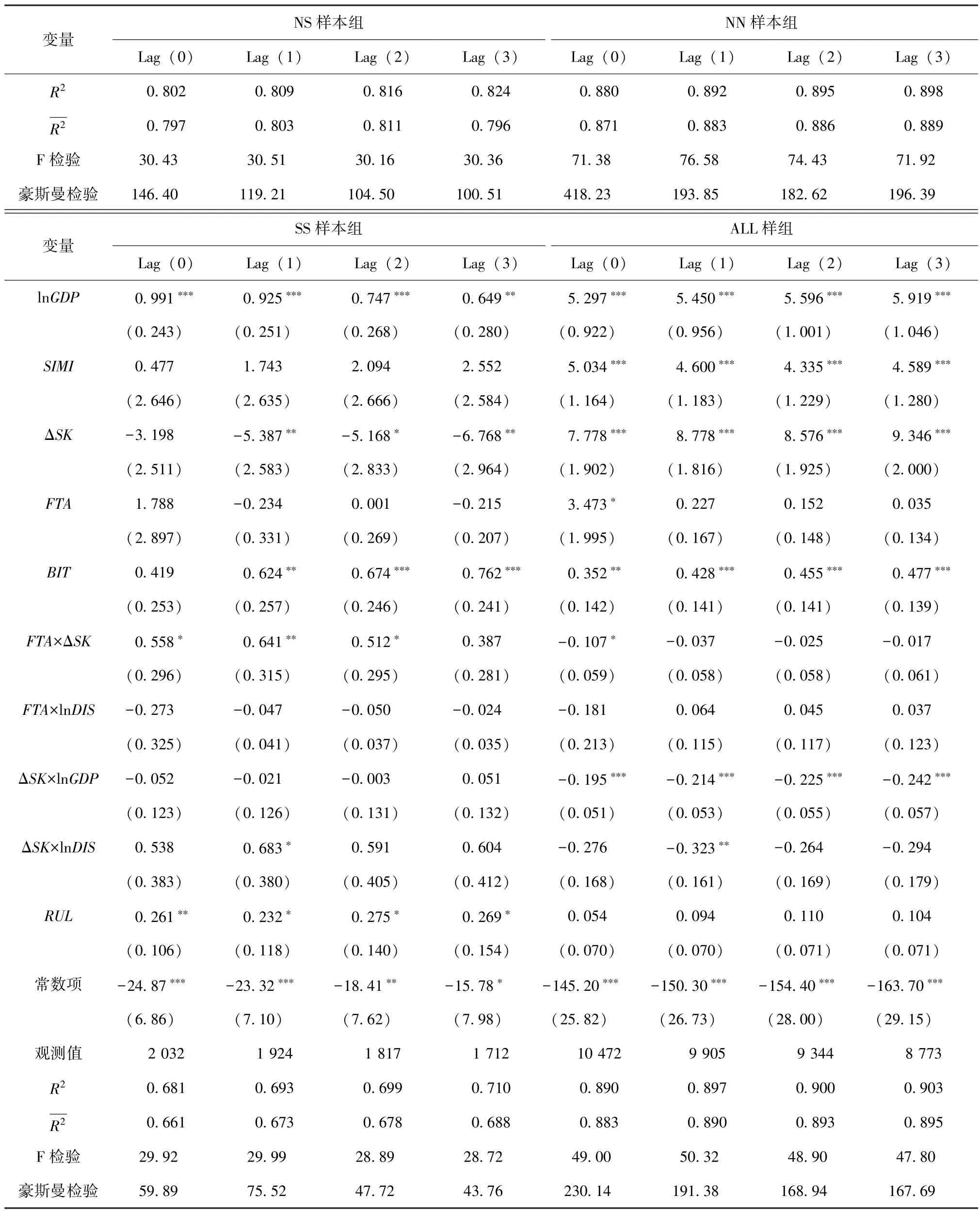
表3（续）

（四） 稳健性检验

跨国企业的对外直接投资行为， 特别是以绿地投资为主的跨国直接投资， 因涉及大规模的固定资产投资， 通常都是长期动态行为， 企业会分批分期持续性投入一段时间， 因此本期投资会受到前期投资的影响。 这意味着模型的被解释变量FDI可能存在自相关问题。 如此将模型设定为静态面板数据模型进行估计将产生动态面板偏差。 本文将采用阿雷拉诺和邦德（Arellano ＆ Bond， 1991）［26］的差分广义矩估计（GMM） 方法进行动态面板估计， 将被解释变量lnFDIijt的一阶滞后项lnFDIijt-1纳入式（1） 右侧解释变量中， 再进行一阶差分：

lnFDIijt-lnFDIijt-1=α（lnFDIijt-1-lnFDIijt-2） + （χijt-χijt-1）′B+ （εi jt-εijt-1）

即：

dlnFDIijt=dlnFDIijt-1+d χijt′B+dεi jt（2）

其中，χ代表所有的解释变量，B代表解释变量的系数矩阵。 考虑到外在的冲击， 例如2008 年金融危机， 可能会同时影响双边FDI 和两国经济规模GDP， 判断解释变量lnGDP可能为内生变量， 其他解释变量设为外生变量。 此外， 考虑到FTA 对FDI 产生影响可能有一定的时滞， 将FTA 当期值和滞后1 期值都纳入解释变量。

为了验证模型设定和工具变量是否合理性， 本文进行了两个检验： 用Arellano-Bond 检验考察模型原假设扰动项ε 无自相关是否成立， 根据扰动项自相关的情况调整工具变量的滞后阶数； 用汉森（Hansen）检验考察工具变量的过度识别假设。 回归结果①限于篇幅， 省略动态模型的稳健性检验回归结果， 备索。表明， 除了ALL 样本组中的Hansen 检验没有通过外， 其他样本组均通过了二阶序列相关和工具变量合理性检验。 其中， NS 样本组中滞后一期FTA 的回归系数为正且在1%的统计水平上高度显著， NN 样本组和SS 样本组的FTA 当期值和滞后一期的回归系数均不显著。 该回归结果与固定效应模型的回归结果一致。

五、结论

本文梳理了双边FTA 影响双边FDI 的核心渠道和路径， 即贸易成本效应、 投资规则效应和市场规模效应。 结合跨国投资的知识资本模型， 本文提出不同于张勇俊（2011）［3］的理论假设： 通过贸易成本效应、 投资规则效应和市场规模效应的综合影响， 发达国家和发展中国家之间的双边FTA 会促进双边FDI，发达国家之间和发展中国家之间的双边FTA 对双边FDI 的影响方向不确定， 取决于三个效应的综合作用。

实证分析方面， 本文采用了固定效应模型和动态面板数据模型估计。 两个模型的回归结果一致， 即NS 样本组的FTA 回归系数显著为正， NN 样本组和SS 样本组的FTA 回归系数均不显著。 这意味着， 在样本范围内， 发达国家和发展中国家之间的NS 型FTA 对双边FDI 具有促进效应， 发达国家之间的NN 型FTA 和发展中国家之间的SS 型双边FTA 对双边FDI 均没有显著影响。 这说明在这两类FTA 中， 影响FDI的正向投资规则效应和市场规模效应， 恰好抵消了负向的贸易成本效应。

本文的结论具有积极的现实意义。 党的十九大报告指出， 要“推动形成对外开放新格局”。 引进外资、 推动对外投资以及构建高标准自由贸易区网络是中国近期对外经济合作的重要方向。 上述研究结论表明， 建设自由贸易区对引进外资和对外投资既可起到推动作用， 亦可起到阻碍作用， 但通过对FTA 内容的合理设置可以减少或规避对外资的不利因素。 具体说来， 中国同发达国家签署的自由贸易协定， 将促进双边直接投资； 中国与发展中国家签署的自由贸易协定， 既可能促进双边FDI， 也可能阻碍双边FDI。因此， 在FTA 谈判中要权衡贸易成本效应和投资规则效应， 较高标准的投资条款可使其对双边FDI 发挥积极效应。