形容词修饰语义的现代类型论探析

2022-05-17罗朝晖石运宝薛涛

逻辑学研究 2022年2期

罗朝晖石运宝薛涛

1 引言

二十世纪初，罗素（B.Russell）等人提出分支类型论（theory of ramified types，[36]），旨在解决朴素集合论中发现的罗素悖论等悖论所导致的对数学基础的信任危机。之后由拉姆齐（F.Ramsey，[31]）指出，分支类型论可“简化”为简单类型论（simple theory of types），并由丘奇（A.Church，[4]）用λ演算将其形式化，被广泛应用；例如，在形式语义学界一直占有统治地位的蒙太古语义学（[34]）的基础便是简单类型论及其模型理论。

现代类型论（Modern Type Theories）始于马丁洛夫（P.Martin-Löf）七十年代对构造性数学基础的研究，有直谓（predicative）和非直谓（impredicative）两种，前者以马丁洛夫类型论（[22,26]）为代表，而后者则包括构造演算（calculus of constructions，[6]）和统一类型论（Unifying Theory of dependent Types，简称为UTT，[12]）。现代类型论源于对数学基础的研究，近年来获得了长足的发展，被广泛应用于形式化建模、逻辑推理、形式语义学等多个领域（[39]）。计算机科学家以现代类型论为基础发展并实现了计算机定理证明辅助工具（proof assistant），有效地应用于数学形式化、程序验证、自然语言推理等等。

近十几年以来，在门尼希（U.Mönnich，[24]）、桑德霍姆（G.Sundholm，[33]）和兰塔（A.Ranta，[32]）等学者早期工作的基础上，运用统一类型论等新的理论进展，基于现代类型论的自然语言语义学（以下简称为MTT 语义学，参考[18,3]）得到了进一步的系统性发展，渐趋成熟。MTT 语义学在逻辑学、语言学及计算机科学等领域的跨学科互动彰显了其在自然语言语义刻画及推理等方面不同于蒙太古语义学的独特优势。本文基于作者有关MTT 语义学的研究成果，在中英文形容词分类的基础上，使用现代类型论丰富的类型结构并结合其强有力的语义描述机制，给出了适合的语义和推理描述。

形容词及其修饰语义是语义学的重点研究领域。本文根据关于形容词的传统分类（[11]），描述了各类形容词在MTT 语义学中的刻画方式。首先，作为一个案例，它表明现代类型论丰富的类型结构足以描述多种多样的语言特征，并且这完全是在以证明论为基础的类型论中进行的（与基于模型论的蒙太古语义学不同）。另外，我们在使用MTT 语义学分析形容词修饰的时候，无需借助于意义公设，这也是此工作的优点之一。

关于形容词语义的研究，学者们自上世纪70 年代以来在蒙太古语义学中做了大量的工作，包括坎普（H.Kamp，[11]）、帕森斯（T.Parsons，[27]）、克拉克（R.Clark，[5]）以及蒙太古本人早期在蒙太古语义学中对形容词进行的分类研究（近期的相关工作，请见莫尔奇基（M.Morzycki，[25]）等）。国内学者也在这方面做了不少相关工作。比如，石运宝和邹崇理（[40]）运用形容词的分类分析一些名词和名词的组合，并就否定性形容词提出了转换中心语的方案，并沿用了莫尔奇基（[25]）就形容词的分析，采用模态方案分析非承诺形容词。刘壮虎（[38]）提出了性质谓词有别于类谓词的想法，构造了专门的逻辑系统针对下属形容词进行刻画，颇有新意。当然，由于可以附加意义公设，人们通常不必为描述某类词汇的语义而改变基础的逻辑语言。

请注意，上面这些工作均是在蒙太古语义学（即简单类型论及其模型理论）中进行的，而本文则是描述如何在现代类型论中给出形容词的语义。比如说，在蒙太古语义学里，普通名词（或简称通名）被解释为谓词，因此形容词对名词的修饰（形-名组合）同样也被解释为谓词；而在现代类型论中，通名被解释成类型，因此形-名组合也要被解释为类型。1将通名解释为类型（而非谓词）有若干优点，这包括得以使用类型检测作为选择限制（selectional restriction）的衡量标准以及在形式语义学中合理使用子类型机制等等。请参见[3]，第1.4.3 节等有关文献。换言之，作为从通名到通名的映射，形容词修饰的MTT 语义应描述为从类型到类型的映射（而不是像在蒙太古语义学那样是从谓词到谓词的映射）。因此，本文关于形容词修饰语义的研究亦可视为一个经典案例，从中可窥见现代类型论丰富的类型结构在描述各种各样的语言学特征时起着关键的作用。

文章各节安排如下：第2 节对MTT 语义学作一概述并简要介绍现代类型论的有关构造，为后文打好基础；第3 节先是简述了形容词的分类及蒙太古语义学关于形容词修饰语义的不足之处，接着研究在现代类型论中如何使用其丰富的类型结构来给出各类形容词的修饰语义；最后，第4 节讨论有关一类特殊形容词（时态形容词）的MTT 语义分析。

2 基于现代类型论的自然语言语义学

本节首先概述基于现代类型论的自然语言语义学（MTT 语义学）及其优点，然后介绍现代类型论的有关类型结构，为后续章节分析做铺垫。

2.1 MTT 语义学概述

MTT 语义学（[18,3]）与蒙太古语义学（[34]）相似，所不同的是前者的语义基础是现代类型论。如表1 所示，在MTT 语义学中，普通名词被解释为类型，动词和形容词被解释为类型为A →Prop的谓词（其中A是与该动词或形容词相关的合理对象所组成的类型），而句子则可解释为类型为Prop的命题。（表1 还给出了副词的语义类型（第四行）及其使用方式（第五行），我们在下文再详细说明）例如，普通名词“猫”可被解释为类型Cat，动词“跑”被解释为谓词，其论域为所有动物组成的类型Animal，而形容词“黑（的）”也被解释为谓词，其论域为所有物体组成的类型Object。请注意，MTT 语义学中将名词解释为类型（[17,32]），这同蒙太古语义学中将名词解释为谓词的方法相比，有若干优点，详见（[3]）。

表1:MTT 语义举例

现代类型论具有丰富的类型结构。简单类型论只有实体类型e，真值类型t以及由它们所产生的e →t等函数类型（〈e,t〉是e →t的另一种表达形式），而现代类型论则包括Π 类型及Σ 类型等依赖类型（dependent types），自然数类型及向量类型等归纳类型（inductive types），以及被称为类型空间（universes）的以类型为元素的类型（包括对应于公式的逻辑类型及类型空间Prop——见2.3 节）。由于具有丰富的类型结构，普通名词在现代类型论中可以解释为类型，而不是像在简单类型论中那样解释为谓词。因此，选择限制（selectional restriction）在MTT语义学中可以用可判定的类型检测（type-checking）来表达，而在蒙太古语义学中它只能用不可判定的逻辑公式的真假来描述。比如，“说话”的蒙太古语义为talkM:e →t，“书”的蒙太古语义BookM:e →t，而在MTT 语义学中“说话”的语义为talk:Human →Prop，“书”的语义为类型Book，因此，“书会说话”的蒙太古语义是(*)，而其MTT 语义则为(**)：

请注意，(*)是合法的逻辑公式，而(**)则不然：因为b不是类型Human的对象，所以talk(b)是不合法的。在蒙太古语义学中，如果一个句子是没有意义的，其语义仍是一个合法公式（它通常为假，但其真假与否是不可判定的），而在MTT 语义学中，一个没有意义的句子的语义是一个非法公式，换言之，一个句子有意义与否化归为判断其MTT 语义是否为合法公式，而且这是可判定的。因此，MTT语义学提供了解决选择限制问题的更佳方式。

现代类型论同时具有模型论特征和证明论特征（[3,19]），表达力非常强，很适合用于刻画自然语言的语义。一方面，由于其模型论特征，它可以凭借丰富的类型结构，细化论域，从而更好地解释复杂的语言现象；另一方面，由于其证明论特征，现代类型论具有与维特根斯坦（L.Wittgenstein）所倡导的“意义即使用”的哲学理念密切相关的“证明论语义”（proof-theoretic semantics，[10,23,30]），并以此为基础借助计算机定理证明辅助工具实现自然语言的推理（对此本文不做详述，感兴趣的读者可参考[3]第六章及有关文献）。

下面先简要给出现代类型论中用于刻画自然语言语义学的基本构造。

2.2 现代类型论中的判断及类型结构

在现代类型论中，判断（judgement）是基本的概念，其表述形式如下：

直观上，(α)是说，在标记（signature）Δ 中，在上下文（context）Γ 做的假设下，a是类型为A的一个对象。需要说明的是，若A是表示逻辑公式的类型，则a:A表示a是A的证明。a:A虽然与集合论中s ∈S以及一阶逻辑公式S(s)很像，但有所不同：a:A是否成立是可判定的，但一阶逻辑公式s ∈S或S(s)的真假则是不可判定的。

(α)中的上下文Γ 是由变元和类型的序对组成的有穷序列，假定xi的类型是Ai（i1,2,...,n）：

在该上下文(β)中，先前的x1,...,xi-1可能出现在后续的类型中，可表示为xi:Ai[x1,...,xi-1]加以强调，表明类型Ai[x1,...,xi-1]可依赖于先前的变元x1,...,xi-1。举例来说，某上下文可/由如下的两个序列组成：

上下文(γ)表示：“x是任意一只猫，并且x是黑的”。这里，x和y是表示任意对象的变元，Cat是由猫构成的类型，而x:Cat则假设x是Cat的任意对象（“x是任意一只猫”）；命题公式black(x)表示“x是黑的”的语义，它也是类型（逻辑类型），而y:black(x)则假设y是black(x)的任意一个证明。这里，类型black(x)依赖于之前出现的变元x，因此是依赖类型。值得一提的是，从上下文(γ)，我们可以使用现代类型论的规则形成如下命题（其中ugly(x)是表示“x是丑的”的命题）：

它是句子“猫只要是黑的就不丑”的语义。

另外要说明的是，虽然现代类型论中的上下文可以用来近似地描述语言学中的语境（linguistic context）或情境（situation），但严格说来并不合适，原因是描述语境或情境应该用常项而非上下文中的变项，这就是判断(α)中的标记Δ 所起的作用（关于标记的讨论可参考[19,3]）。本文后续章节不再使用或讨论标记，所以在书写判断时将一概将其略去，把Γ⊢Δa:A简化为Γ⊢a:A。

如上所述，现代类型论采用依赖类型等工具，其丰富的类型结构涵盖了逻辑公式、普通名词、形容词、副词、并列词以及其他复杂的语言学现象。下面挑选若干典型的、常用的几种类型加以说明，后面分析形容词修饰的时候也会用到。

函数的依赖类型（Π 类型）现代类型论包含若干种依赖类型，函数的依赖类型（Π 类型）是其中一种。如果A是一个类型，且B(x)也是个类型，其中B(x)依赖于类型为A的对象x，那么Πx:A:B(x)是满足如下条件的函数f的类型：对于任意的a:A，f(a)的类型为B(a)。注意，f作用于a所得结果f(a)的类型B(a)依赖于输入a，这就是Π 类型是依赖类型的原因。举个例子来说，假设Human是所有人所组成的类型，对于每个x:Human，Parent(x)是x的父亲或母亲的类型，那么，我们可以考虑Π 类型Πx:Human.Parent(x)，其元素是满足如下条件的函数f：对于任意的h:Human，f(h)的类型是Parent(h)，即f(h)是h的父亲或母亲。

在现代类型论中，各种类型结构由自然演绎推理的规则来归纳定义。这些规则一般包括该类型的形成规则、引入规则、消去规则和计算规则。就Π 类型来说，这四类规则分别是（对Π 类型而言，每一类只有一个规则）：

Π 类型的形成规则它规定了如何构造Π 类型：

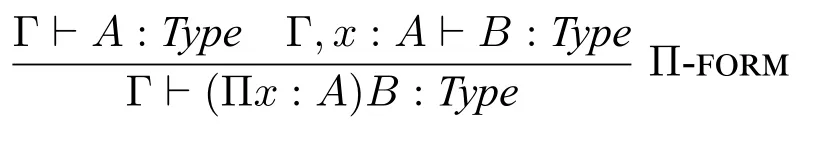
这条规则是说，若A在假设Γ 下是类型并且B在假设Γ,x:A下是类型的话，那么，在上下文Γ 中，Πx:A.B是类型。

Π 类型的引入规则（或称抽象规则）它规定了Π 类型的对象是使用λ所表示的函数项（λx:A.b是类型为Πx:A.B的对象）：

Π 类型的消去规则（或称应用规则）它规定了λ函数应用过程，其中B[a/x]是将B中x的自由出现替换为a所得到的结果：

Π 类型的计算规则（或称β 转换规则）给予应用运算以含义，指出当λ表达式作用到论域中的对象时计算如何进行：

举例来说，一个类型为Πx:Human:Parent(x)的函数f，应用到一个人h后，其函数值f(h)是类型为Parent(h)的父亲或母亲，而不会是别的值。注意，x:A在b或B中可能自由出现，因此，在计算上述等式左侧的表达式时，a不仅要在b中替换x的自由出现，而且相应的替换也要在B中进行，因为b和B都可能依赖于x。

当x不在B中自由出现时（即当B是常数类型时），Π 类型Πx:A.B退化为通常的函数类型，记为A →B。换言之，函数类型是Π 类型的特殊形式，它的例子已在第2.1 节用过（如Human →Prop等）。

序对的依赖类型（Σ 类型）另一种典型的依赖类型是序对的依赖类型（Σ 类型）。如果A是一个类型，且B(x)也是个类型，其中B(x)依赖于类型为A的对象x，那么Σx:A.B(x) 是由序对(a,b) 组成的类型，其中a的类型是A，b的类型是B(a)。与Σ 类型相关的是投射运算π1和π2，它们满足如下等式：对于类型为Σx:A.B(x)的(a,b)，π1(a,b)a且π2(a,b)b。

举例来说，如果的Cat是猫的类型，black(x)是表达“x是黑的”这一命题，那么：Σx:Cat.black(x)是黑猫的类型，该类型中的对象是序对(c,p)，其中c是一只猫，而p是命题“c是黑的”的一个证明。请注意，black(x)依赖于x，因此p的类型是black(c)，它依赖于c。关于此例还有一点需要说明，这里使用了“命题即类型”（propositions-as-types）的原则（见第2.3 节）：black(x)是逻辑命题，因此也是类型，所以可以形成上述Σ 类型。一般说来，当P(x)是一个逻辑命题时，Σ 类型Σx:A.P(x)是A的子类型，记作Σx:A.P(x)≤A（关于现代类型论的子类型理论，请参考[13,21]等相关文献）。Σ 类型的引入规则和消去规则如下：

Σ 类型的引入规则

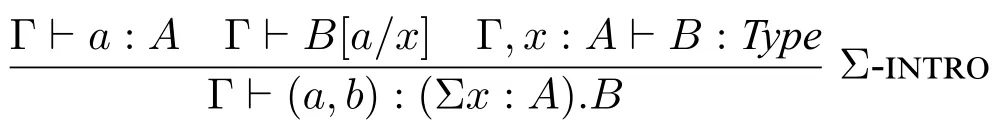
在上述规则中，由于B可能依赖于x（或者说x可能自由出现于B中），序对(a,b)的第二个元素b的类型B[a/x]依赖于第一个元素a。这种依赖关系也是为什么称Σ 类型为依赖类型的原因。

Σ 类型的消去规则（引入π1 及π2 两个消去算子）

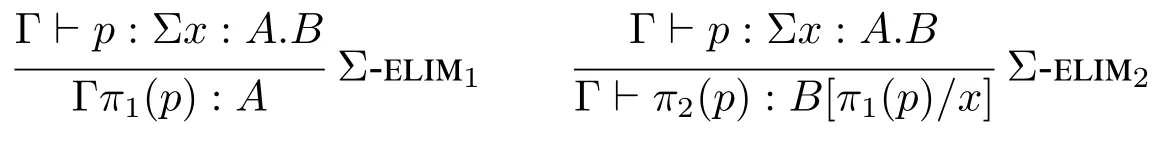
另外，当x不在B中自由出现时（即B是常数类型时），Σ 类型Σx:A.B退化为通常的积类型（product type）A×B。换言之，积类型是Σ 类型的特殊形式，例子有Human×Cat等。

不相交并类型如果A和B是类型，则可形成不相交并类型（disjoint union type）A+B。如下述引入规则所示（由于篇幅原因，其他规则略去），A+B的对象要么是inl(a)，要么是inr(b)，其中a和b分别是A和B的对象。

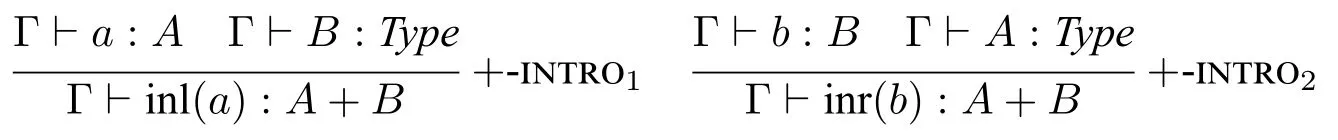
请注意，现代类型论与集合论不同，没有类型的“交”或“并”运算。例如，若A和B为类型，可以构造它们的不相交并类型A+B，它和A或者B没有共同的对象（例如，如果a:A，则inl(a):A+B，但a和inl(a)是不同的对象）。

3 类型空间

直观地讲，类型空间（universe）是类型的类型。换句话说，一个类型空间是个类型，而这个类型中的所有对象也都是类型。在此我们介绍逻辑类型空间Prop（所有逻辑公式的类型空间）和在MTT 语义学中所使用的CN（普通名词语义所构成的类型空间），在本文后续章节里会用到它们。

逻辑类型空间Prop在统一类型论（[12]）这样的非直谓类型论中，所有逻辑命题构成一个类型Prop。它的引入规则（即∀公式的形成规则）为：

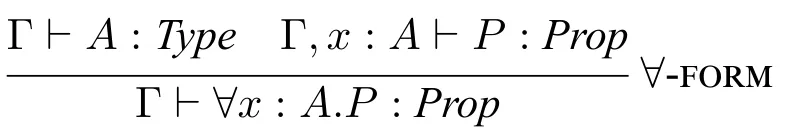
现代类型论遵循“命题即类型”（[7,9]）的理念，每个命题均是类型，如下述规则所示：

因此，Prop是一个类型空间，其对象均是类型。

读者可能已经注意到，上述Prop的引入规则（即∀公式的形成规则）和Π 类型的形成规则（Π-FORM）非常相似，并且这些全称量化公式的证明也是λ表达式（λx:A.p等）。与Π 类型不同的是，∀公式的形成可以是非直谓的。例如，Prop是一个类型，因此根据如上的规则，我们便可形成命题∀x:Prop.x，它也是Prop中的对象。由于Prop是非直谓性类型空间，我们可使用∀来定义其他逻辑运算符（⇒、∧、∨及∃等）。例如，P ∧Q∀X:Prop.(P ⇒Q ⇒X)⇒X。

另外，由于Prop是类型，它可同其它类型构造一起使用。例如，若A为类型，则A →Prop是论域为A的谓词所组成的类型（我们已在前面见过有关例子了）。

普通名词的类型空间CN在MTT 语义学中，类型空间的概念有着广泛的用途，与Π 类型结合使用，它还有助于表达语义上的多态概念，我们亦将此称为Π 的多态机制（Π-polymorphism）。下面对此以普通名词的类型空间CN为例加以说明。

CN是所有普通名词（的语义）所组成的类型空间（[16,18]）。举例说来，CN中的对象包括“书”的语义Book、“猫”的语义Cat、“黑猫”的语义Σx:Cat.black(x)等等。CN及其相关的Π 的多态机制在语义构造时非常有用。例如，它可以用来为修饰动词的副词赋予语义（[16]）；在第2.1 节表1 中（第四行）副词“快”的语义quickly的类型为ΠA:CN.(A →Prop)→(A →Prop)，因此，“猫跑得快”、“张三走得快”等等均可用此语义解释。还有许多使用CN及其相关的Π 的多态机制的例子，比如在MTT 语义学中解释下属形容词就会用到——见第3.2 节。

表2:形容词分类

4 形容词修饰：MTT 语义学的一个应用

根据逻辑语义学对形容词的传统分类（[5,11,27]），形容词可划分为如表2 所示的四个主要类别：相交（intersective）形容词、下属（subsective）形容词、否定性（privative）形容词及非承诺（non-committal）形容词。2这一形容词分类着重考虑其推理性质。这与其它分类原则的着眼点不同。例如，汉语形容词有[41]等各种分类方法，其用途亦不同。另外，关于形容词可否用作定语以及“形容词+名词”所组成的词组是句法结构还是复合词等问题，汉语和英语亦有不同之处。有关课题有待进一步研究，在此不作讨论。表2 第二栏给出了各类形容词A修饰名词N时应有的推理模式，而第三栏则给出简例。

相交形容词的例子有“黑（的）”“漂亮（的）”和“法国（的）”等等。以“黑猫”为例，相关推理为：“黑猫”既是黑色的又是猫。从某种意义上说，相交形容词“黑”作为物体的属性与该物体是什么并无关系。但下属形容词则与此不同，其语义取决于所修饰名词代表的种类。例如，熟练的外科医生作为外科医生是熟练的，但这并不意味着此人做什么都熟练。诸如大/小、高/矮等有关尺寸的形容词也是如此。小象作为象类动物体积较小，但和像鱼虾之类动物相比就并不小了。换言之，下属形容词的语义依赖于所修饰的名词，而相交形容词则不然。当使用否定性形容词修饰普通名词时，所得词组的属性和原名词相反（在表2 中我们用否定符将此表示为“¬N”）。例如，通常说来，“假枪”并不是枪。非承诺形容词是我们考虑的最后一类，使用它们所得的词组既可能具有被修饰名词的属性，但也可能没有。比如“被指控的”（alleged）就是这样一个非承诺形容词：被指控的贼可能是贼也可能不是。使用形容词修饰名词词组这一过程可建模为从名词词组到名词词组的映射。在传统的蒙太古语义学（[34]）中，名词词组的语义是表示“属性”（property）的谓词，其类型为e →t。因此我们可以将形容词对名词的修饰过程描述为从属性到属性的映射。以“黑猫”为例，形容词“黑”的语义类型为(e →t)→(e →t)（或e →t），而“猫”的类型为e →t，将这两者组合而得到“黑猫”的语义，它也是一个表示属性的谓词，其类型仍为e →t。

在蒙太古语义学中，如上所述的形容词分类可刻画如下（[11]）。假设某形容词的语义为谓词A:e →t，某名词的语义为N:e →t,则使用该形容词修饰该名词的语义[AN]具有如下性质：

· 相交形容词：∀x:e.[AN](x)⇒A(x)∧N(x)

· 下属形容词：∀x:e.[AN](x)⇒N(x)

· 否定性形容词：∀x:e.[AN](x)⇒¬N(x)

· 非承诺形容词：对非承诺形容词而言，[AN]没有约束条件。

在蒙太古语义学中，人们不得不采用所谓的“意义公设”（meaning postulate)作为额外条件对语义加以限制，以保证上述性质对下属形容词和否定性形容词成立。例如，“假（的）”是否定性形容词，其有关的意义公设则包括“假枪不是枪”等等。需要指出的是，采用意义公设是人们的无奈之举，原因是，在蒙太古语义学使用的简单类型论中，定义形容词修饰语义时无法用语义类型来直接表达这些性质。在MTT 语义学中，我们则不再使用这些额外的意义公设，而直接描述各类形容词修饰的语义类型。

与蒙太古语义学不同，在MTT 语义学中普通名词被解释为类型（见第2.1 节），因此我们可以把形容词对名词的修饰过程描述为从类型到类型的映射，它将一个形容词的语义（建模为谓词）和一个名词的语义（建模为类型）相组合，其结果为一个新的类型。以下诸小节将讨论针对各类形容词如何设计这样的映射来描述形容词修饰语义（见表3）。

表3:形容词修饰的现代类型论描述机制

4.1 相交形容词

在MTT 语义学中，现代类型论的Σ 类型可同强制性子类型理论（coercive subtyping,[13,21,37]）一起用来描述相交（intersective）形容词修饰语义（[14,18]）。3用Σ 类型描述形容词修饰语义的想法最初由门尼希（[24]）及桑德霍姆（[33]）提出，并由兰塔（[32]）做了进一步研究。然而，由于没有适当的子类型机制，所提出的建模方法并不理想（有关这方面的详细讨论，参见[14,18,3]）。名词词组和形容词在MTT 语义中分别被解释为类型和谓词。例如，“黑”的语义black是以所有物体的类型Object为论域的谓词，其类型为(1)。因此，若“猫”被解释为类型Cat，则“黑猫”的语义为(2)中的Σ 类型。

请注意，虽然black的论域并不是x的类型Cat，但是由于子类型关系(3)，black(x)以及(2)中的Σ 类型仍是正确的。并且，子类型关系通过Σ 等类型构造算子所传播4子类型通过类型构造算子的传播由相应的推理规则所描述（[13]）。例如，有关Σ 的规则如下，其中d 将(a,b)映射为(c(a),c′[a](b))：上述由(3)到(4)的推理据此而得。。例如，由于子类型关系(3)，因此(4)为真：所有黑猫都是黑的物体。

值得强调的是，上述方法必须满足两个条件才是正确可行的。首先，第一个要满足的条件是：相交形容词做修饰时的推理性质(5-6)成立。由(7-8)可知，这两个推理性质成立。以“黑猫”为例，(9-10)均成立。

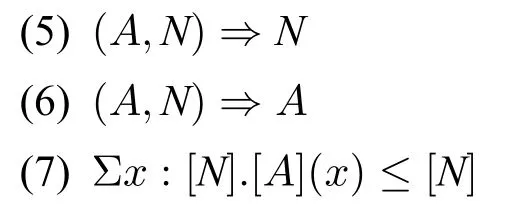
(8) 如果p:Σx:[N].[A](x)，则[A](π1(p))为真。

(9) 黑猫是猫。（Σx:Cat.black(x)≤Cat）

(10) 黑猫是黑色的。（若(c,b):Σx:Cat.black(x)，则b:black(c)。）

第二个条件是，在现代类型论中，称为“证明的不相关性”（proof irrelevance）的性质需成立，以保证上述方法的正确性。这点略显微妙，虽然重要但很少被人们意识到。仍以“黑猫”为例，根据直觉，两只黑猫是同一只黑猫当且仅当它们是同一只猫，至于如何证明它们是黑色的无关紧要。若以Σx:Cat.black(x)表示黑猫的语义（见(2)），假如c:Cat且p和q均为black(c)的证明，则应有pq。这就是证明的不相关性。

值得一提的是，能否在现代类型论中引入证明不相关性原则取决于在该类型论中可否明确区分逻辑类型和其他类型。这在统一类型论（[12]）等非直谓类型论中是可行的，但在直谓的马丁洛夫类型论MLTT（[23,26]）中则不然（在MLTT中逻辑命题和类型不加区分，因此证明的不相关性就意味着所有类型要么是空的要么就是单点类型，这显然是荒谬的）。如若有人喜欢使用直谓类型论研究MTT语义学，需要寻求新的途径。例如，我们在[20]中提出不再使用MLTT 的Pat 逻辑，而增加HoTT 的逻辑系统（[35]）从而将MLTT 扩展为MLTTh，用以研究MTT语义学（有关详情及讨论，请参见[17,20]）。

4.2 下属形容词

首先说明，像描述相交形容词那样使用简单谓词来描述下属形容词的语义是错误的。例如，如果“大象”和“动物”分别解释为类型Elephant和Animal（Elephant ≤Animal ≤Object），形容词“小”的语义用简单谓词SMALL:Object→Prop来描述，并使用Σ 类型(11)和(12)分别解释“小象”和“小动物”，那么由于子类型关系(13)，我们将错误地得出结论(13)，说每只小象都是小动物。

在MTT 语义学中，下属形容词的语义可使用Π 类型及与类型空间CN相关的多态机制来描述（[1,2]）（亦可将它们的语义称为“多态谓词”）。例如，“小”的语义为具有类型(14)的多态谓词small。若某普通名词的语义为N:CN，谓词small(N):N →Prop。对不同的普通名词N1和N2，small(N1)和small(N2)也可能不同：比如，small(Elephant)和small(Animal)是不同的谓词。由此，“小象”和“小动物”便可分别解释为(15)和(16)。这样的话，我们将无法再得出像“小象是小动物”这样的错误结论。

显然，上述语义满足有关下属形容词修饰的推理要求(A,N)⇒N。例如，我们有(17)，即每个小动物都是动物。

4.3 否定性形容词

否定性（privative）形容词的例子有“假”“假想（的）”和“虚构（的）”等等。通常，人们认为它们表达某种否定性质，由它们修饰所形成的名词词组同被修饰名词的性质相反——如(18)以及例(19)所示。

(18) (A,N)⇒¬N

(19) 假枪不是（真）枪。

值得指出的是，人们对这类形容词是否确实具有如(18)所示的否定性并无普遍共识。例如，帕蒂（B.Partee，[28,29]）认为，“假”这类形容词并没有(18)意义下的否定性，它们实际上同下属形容词类似，其解释应和下属形容词相似并同时使用类型转换（type-shifting）和语义转换（coercion）加以完善。比如在例(20-21)中，帕蒂认为名词“皮子”的语义应该同时包括真毛皮和假毛皮。

(20) 我不在乎那个皮子是假皮子还是真皮子。

(21) 我不在乎那皮子是假的还是真的。

在MTT 语义学中，罗朝晖（[15]）提出了用不相交并类型（见第2.2 节）描述否定性形容词的想法，并在做了进一步发展（[3]）。下面我们以“假枪”为例进行说明。首先，直观地讲，所有枪支组成的类型可以认为是由真枪和假枪共同组成。使用不相交并类型可将此形式化如下（所有枪支的类型G可定义为GR+GF，其中GR和GF分别是真枪和假枪组成的类型）：

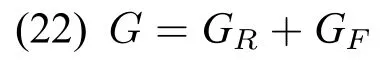
如此给出枪支的类型，我们则可以定义如下谓词：

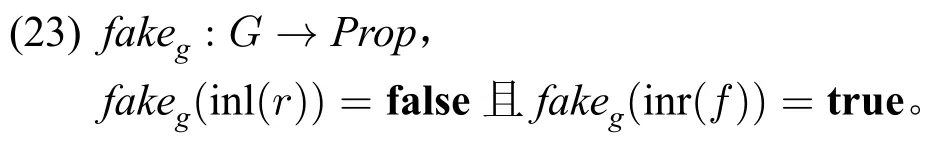
然后，我们可以使用Π 类型和基于类型空间CN的多态机制给出诸如“假”等否定性形容词的通用类型(24)。如(25)所示，就“枪支”而言，“假”的语义正是上面所定义的fakeg，而“假枪”的语义可定义为(26)。

(24) 是说，“fake”的类型为ΠA:CN.(A →Prop)，同理，“real”的类型也是ΠA:CN.(A →Prop)，表明输入的对象A的类型是CN。

根据如上定义，下面的句子(27)及其语义(28)为真：

请注意，上述在MTT 语义学中定义否定性形容词修饰语义的方法符合帕蒂的观点（[28,29]），即否定性形容词实际上是从属形容词——我们像处理从属形容词那样，使用Π 多态机制来给出否定性形容词的类型。虽然产生此想法的背景截然不同，但仔细推敲，它在非形式层面与帕蒂的想法有某些相似之处，读者可做进一步推敲。

4.4 非承诺形容词

非承诺（non-committal）形容词的例子包括“被指控（的）”“潜在（的）”“有争议（的）”等等，其修饰语义没有任何推理性质的要求。例如，被指控的罪犯可能是罪犯，但也可能不是。对这类形容词的修饰语义无需进行一般性刻画。以“被指控（的）”为例：被指控的杀人凶手是被某人指控为杀人凶手的人。

每个非承诺形容词Adj 可用一个以Prop为论域的谓词来描述其语义（Prop的子集）。令Human为所有人的类型。对任意h:Human，此谓词的类型是：

(29)HAdj(h):Prop →Prop

如下例句(30)和(31)可分别解释为(32)和(33)，其中命题murder(y)是“y是杀人凶手”的语义。

(30) 张三是被指控的杀人凶手。

(31) 李四讨厌所有被指控的杀人凶手。

5 关于时态形容词的讨论

时态形容词包括“以前的”（former）、“未来的”（future）等等，它们可以用来修饰普通名词，如下面的例子所示：

(34) 他是以前的总统。（He is a former president.）

(35) 他是我以前的老师。（He is my former teacher.）

如同道蒂（D.Dowty）等人所建议的那样（[8]），former 是一个否定性形容词，由这一类形容词加名词构成的“形-名”结构短语有如下推理性质：

因此，(34)蕴涵(37)，(35)蕴涵(38)。

(37) 他不是现在的总统。（He is not the current president.）

(38) 他目前不是我的老师。（He is not my current teacher.）

道蒂等人在书籍（[8]）中使用了时间模型来刻画former 等作为否定性形容词的语义（亦见[25]等的有关描述）。

如果同意道蒂等人的观点，将“以前的”（former）等视为否定性形容词，那么在MTT 语义学中，它们的语义与“假（的）”（fake）相似，可使用不相交并类型及Π 多态来描述（见第3.3 节）。例如，若PRcurrent、PRformer和PRfuture分别是由当前的总统、以前的总统和未来的总统所组成的类型，则可作如下定义5这里，我们允许former 用于任何一个通名。有人可能认为这不太合适，觉得former 应该只用于某些通名。对此，我们可以使用CN 的一个子类型CNs ≤CN 作为former 的论域。（CNs 的s 表示CNs 中的通名是“stage level common nouns”——请参见[2]的有关讨论。）：

这样的话，与第3.3 节结尾的例子(27) 相类似，我们将得到(34) 蕴涵(37) 以及(35)蕴涵(38)的推理结果等等。

然而，也可能出现以下这些例子所描述的微妙情形：

(39) 他是我以前的（初中）老师，碰巧是我现在的（大学）老师。

(40) 他是以前的总统，碰巧也是这一届的总统。

如果将上述例子所示的种种情况考虑进来的话，那么在描述former 等时态形容词的语义时就需要考虑其他的因素，较仔细地描述时间等概念（就像道蒂等人使用的时间模型那样）。在MTT 语义学的框架下，亦可考虑时间参数，比如普通名词“总统”的语义可被参数化，成为类型President(t)，其中t为时间类型Time的对象，从而给出相应的语义（在此不作详细讨论；请参见（[2]，第21-24 页））。