固体蓄热砖孔道结构参数对蓄/释热性能的影响

毕月虹， 吴 娟， 鲁一涵

(1.北京工业大学城建学部， 北京 100124； 2.绿色建筑环境与节能技术北京市重点实验室， 北京 100124)

经济的快速发展和人们生活水平的不断提高，造成了环境污染日益加剧. 目前，我国的空气污染主要集中在华中华北地区，重度雾霾主要发生在北方冬季[1]. 到2016年底，我国北方地区城乡建筑取暖总面积约206亿m2，燃煤取暖面积约占总取暖面积的83%，以燃煤为主的供暖结构，是造成北方地区冬季雾霾频发的诱因之一[2]. 电能作为一种清洁能源，采用固体电蓄热装置作为热源，可以有效减少因传统燃煤造成的环境污染，是解决冬季供暖污染问题的有效途径，同时，电加热固体储能技术通过将非峰值电转化为热能存储起来，可以实现电力调峰.

已有的文献中大多采用实验和数值模拟等方法，研究集中在蓄热材料选择、蓄热装置结构、电加热装置的布置等方面. 目前固体电加热储能装置的蓄/放热性能还有待改进，在实际应用中由于蓄热体的导热性能差，其热量无法实现高效存储与释放，造成电热元件和靠近电热元件的砖体由于热量堆积而损坏，降低了电热元件和蓄热砖的使用寿命. 开发热导率大的蓄热材料是解决上述问题的一种途径[3-5]，考虑到新的蓄热材料往往由于其制作方法复杂和成本较高，难以得到大范围的推广. 蓄热砖作为储能装置的基本组成单元，研究蓄热砖的孔道结构和进口空气流速对改善电加热储能装置的温度分布和提高其蓄/释热性能同样具有重要的意义.

Lizarraga-Garcia等[6]以具有嵌入式管式热交换器的固体储能系统为研究对象，分析了传热结构和操作策略(层流和湍流)对固体蓄热模块传热性能的影响，得出添加传热结构的蓄热模块在湍流状态下，放热效率、放热时间以及蓄热成本最优. Jian等[7]采用改进的集总参数法，提出了一种既考虑储热量又考虑材料成本的固体储能模块设计方法，结果表明单位存储容量的材料成本仅受能量利用率和圆柱形存储模块的内外半径比的影响. 胡思科等[8-10]对以氧化镁为蓄热材料的固体蓄热装置进行了仿真研究，分析了蓄热体的孔形、孔数、孔道的布置方式及蓄热体的串、并联组合形式对其蓄/放热性能的影响，结果表明圆形孔道相比方形孔道蓄热更快，椭圆竖向布置比圆形和椭圆横向布置蓄热更快，蓄热体串联有利于均衡放热. 鞠亮亮等[11]对氧化镁耐火砖的形状和排布进行研究，分析比较了蓄热过程中不同宽高比矩形孔道耐火砖顺排和不同长短半轴椭圆形孔道耐火砖交叉排布的热性能. 苏驰[12]从蓄热材料和结构方面出发，以蓄热率、表面温度、出风口温度作为评价指标，对固体蓄热装置的蓄热材料、蓄热通道宽度、蓄热通道高度、保温板厚度和出风口结构等进行优化. 东北大学的张雪平等[13]基于某企业实际运行的固体电蓄热装置，建立了热- 流- 固三维耦合传热数学模型，分析了蓄热装置的温度场和应力场，对比了3种不同孔隙率、电热丝排布方式对蓄热体温度分布均匀性和热膨胀量的影响.

本文结合工程实际中的蓄热砖结构，基于流固耦合换热原理，利用ANSYS有限元分析软件中的Workbench模块，对不同结构固体蓄热单元的蓄/释热过程进行仿真研究，分析和比较了蓄热砖孔道结构和进口空气流速等参数对蓄热单元蓄/释热性能的影响，研究结果为蓄热砖孔道结构的优化及进口空气流速的选择提供一定参考依据.

1 物理模型

本文结合工程实际中的蓄热砖，砖体结构如图1所示，砖体尺寸为240 mm×90 mm×150 mm，在保持蓄热砖体积和通风孔道总横截面积不变的情况下，改变矩形孔道和半圆形孔道的尺寸，得到4种结构的蓄热砖，其中矩形孔道的宽高比(L∶H)有 2∶1、8∶1和18∶1三种类型. 砖体孔道结构的几何参数如表1所示.

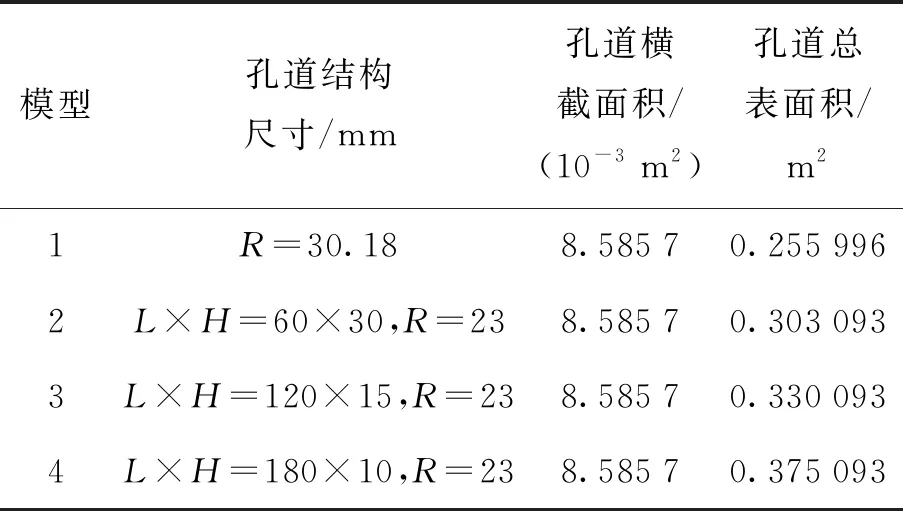
表1 蓄热砖通风孔道的几何参数

图1 蓄热砖结构示意图

为了简化计算，蓄热单元物理模型建立过程中作出如下假设[13-14]：

1) 蓄热材料和电热丝材料为均相介质，热物性参数已知且恒定.

2) 电热丝的横截面积相对于整个蓄热单元而言非常小，为了便于划分网格，将其看作棒热源处理.

3) 蓄热单元的外壁面绝热，与环境没有热量交换.

4) 在蓄热单元的蓄/释热过程，空气流入方向与蓄热单元入口截面垂直.

整个蓄热装置各部分温度分布大致相同，因此可以从蓄热装置中选取一个蓄热单元进行模拟分析，为了便于放置电热丝，选取成对的氧化镁蓄热砖组成的蓄热单元，将电热丝放置在由纵向半圆孔道对接组成的圆形孔道中.采用Workbench自带的三维建模软件DesignModeler，分别对4种结构的蓄热单元进行建模，其中模型2的简化结构如图2所示.

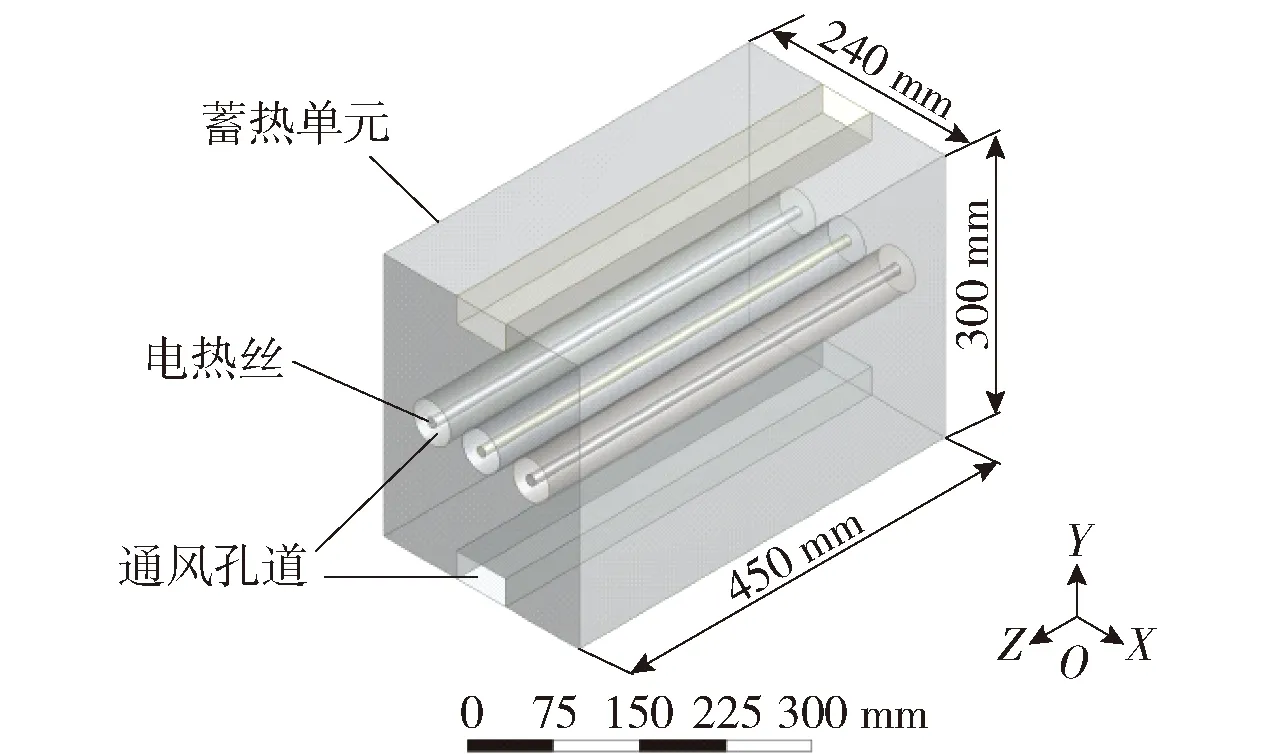
图2 蓄热单元的物理模型(模型2)

2 数学模型

2.1 控制方程

电加热固体储能装置在蓄热时包含3种传热过程，即电热丝与蓄热单元之间的辐射换热，空气与蓄热单元、电热丝的耦合对流换热，蓄热单元内部的热传导[15].释热时只有空气与蓄热单元的耦合对流换热和蓄热单元内部的热传导，根据电加热固体储能装置的传热原理，建立如下控制方程[13-14,16].

1) 流体域控制方程

质量守恒方程：

(1)

动量守恒方程：

(2)

能量守恒方程：

(3)

式中：ρf为空气的密度，kg/m3；vf为空气的流速，m/s；hf为空气的焓，kJ/kg；p为压强，Pa；μf为空气的动力黏度，kg/(m·s)；I为单位张量；λf为空气的导热系数，W/(m·K)；τf为剪切力张量；Sf为内热源.

2) 固体区域控制方程

在蓄热单元内部只有热传导过程，满足导热微分控制方程

(4)

式中：ρs为蓄热单元的密度，kg/m3；Cs为蓄热单元的比热容，J/(kg·K)；Ts为蓄热单元的温度，K；λs为蓄热单元的导热系数，W/(m·K)；qv为蓄热单元内部体积热源，W/m3.

3) 流固耦合界面方程

流动的空气与蓄热单元之间满足流固耦合关系

Tf=Ts|(温度连续)

(5)

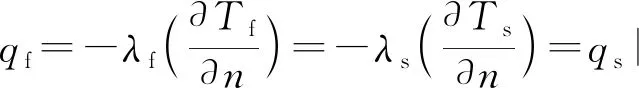
(6)

式中：Tf为空气温度，K；qf和qs分别为流- 固交界面上空气侧和蓄热体侧的热流密度，J/(m2·s)；n为流- 固交界面法向量.

利用雷诺数可判断空气的流动是层流或湍流，雷诺数的计算公式为

(7)

式中d为特征长度，m.

2.2 初始及边界条件

蓄热时，电热丝恒功率加热，电热丝单位体积发热功率设为1.305 4×107W/m3.为防止蓄热体局部过热，向蓄热体通入适量空气，空气流速为0.1 m/s，入口温度为293 K，空气采用速度入口和压力出口边界条件.通过计算4种结构蓄热单元的空气雷诺数，得知换热介质空气的流动均属于层流.蓄热单元的初始温度均匀为323 K，四周壁面采用绝热无滑移边界条件.蓄热过程中电热丝温度较高，需要考虑电热丝与蓄热单元之间的辐射换热，本文选用DO辐射模型[13]，初始化选择从速度入口开始，总的蓄热时间为43 200 s.为了使迭代便于收敛，开始时间步长设为0.01 s，计算一段时间后，时间步长设为100 s，镁砖和电热丝材料的热物理性能参数如表2所示.

地毯一般是用来装饰的，然而日积月累，地毯本身会滋生很多细菌、螨虫和灰尘等，会对人的健康产生不好的影响。这张线圈式可加热地毯能够连接到发热片上，把水加热至60℃以上将细菌杀死，还你一张健康美观的地毯。

表2 热物理性能参数表

释热时，电热丝停止加热，空气流速设为1.5 m/s，经计算得到模型4的空气雷诺数最小，数值为2 044，4种结构蓄热单元的空气流动均属于湍流，采用标准k-ε方程求解[15].蓄热单元的初始温度采用蓄热结束时蓄热单元的温度，四周壁面采用绝热无滑移边界条件，释热过程不考虑热辐射，总的释热时间为43 200 s，时间步长的设置与蓄热过程一致.

2.3 网格无关性验证

网格的数量决定了数值模拟结果的准确性，利用Meshing对模型2进行网格划分，划分的网格数分别为39 198、84 189和148 271.通过对蓄热单元进行数值模拟，得到不同网格数下蓄热单元平均温度随蓄热时间变化的曲线，如图3所示.3种网格数的蓄热单元平均温度的变化曲线基本重合,为了提高计算机的效率，在保证模拟精度的前提下，选择39 198网格数进行研究.

图3 不同网格数下蓄热单元平均温度随蓄热时间的变化

3 蓄热数值模拟结果与分析

3.1 不同结构蓄热单元温度场的比较

在相同边界条件下，对4种结构蓄热单元进行蓄热过程的流固耦合数值模拟，观察4种结构的蓄热单元在蓄热结束时刻截面(z=0.225 m)温度场的变化，用Fluent模拟出的蓄热单元截面温度分布云图如图4所示.

图4 蓄热单元截面(z=0.225 m)温度分布云图(蓄热结束)

由蓄热单元的温度分布云图可以看出，在靠近电热丝通道的区域，蓄热单元的温度较高，距离电热丝越远的区域，温度越低，蓄热单元内部出现温度分层现象.这是因为蓄热时电热丝通过辐射和对流将热量传递到蓄热单元的通道内侧，热量通过导热的方式继续由蓄热单元的内侧向外侧传递，热量的传递需要时间，因此远离电热丝的区域形成低温区；蓄热43 200 s，模型1中靠近电热丝通道表面的温度值最高可达883 K，与远离电热丝通道区域的温差值最大为37 ℃.在添加矩形孔道后，蓄热单元的温度分布不均匀性得到改善，靠近电热丝区域的局部高温值降低，随着矩形孔道宽高比从2∶1增大到18∶1，局部高温值由870 K降低到857 K.这是因为在蓄热砖上添加矩形孔道后，空气和矩形孔道表面进行对流换热，矩形孔道周围区域与电热丝通道周围区域的温差增大，热量在蓄热单元内部的传递速度加快.随着矩形孔道宽高比增加，空气与矩形孔道的换热面积增大，换热增强，热量从电热丝周围的高温区域传递到蓄热单元边界的速度加快，因此在蓄热砖上添加矩形孔道能够有效降低热量的局部堆积，避免热应力集中给蓄热单元带来的不利影响.

3.2 电热丝的平均温度比较

图5为不同结构蓄热单元的电热丝平均温度随蓄热时间的变化.

图5 电热丝平均温度随蓄热时间的变化

由图5可知，在相同孔道横截面积下，不同孔道结构蓄热单元的电热丝对应的平均温度变化曲线上升趋势相同.在通电加热初期，电热丝温度迅速升高至850 K，之后电热丝的温升速率骤降，随着时间的推移，电热丝的温度开始逐渐升高.这是因为电热丝通电加热后产生的热量主要通过辐射和对流的方式传递给蓄热单元，加热初始阶段，电热丝温度较低，与蓄热单元的辐射换热量可以忽略，电热丝的温度迅速升高，随后更多的热量开始通过辐射和对流传递给蓄热单元.

3.3 蓄热单元平均温度及温升速率的比较

图6为不同结构蓄热单元平均温度及温升速率随时间的变化.在蓄热0～15 000 s，4种结构蓄热单元的平均温度及温升速率随蓄热时间的变化曲线基本重合，蓄热单元平均温度的上升趋势体现了镁砖良好的蓄热特性，之后模型1的平均温度及温升速率逐渐高于带有矩形孔道的蓄热单元，并且矩形孔道宽高比越大，蓄热单元的平均温度及温升速率越低，表明了不同结构蓄热单元的蓄热能力不同.到蓄热结束时刻，模型1的平均温度最高，温度为869 K，模型4的平均温度最低，温度为843 K.在整个蓄热过程中，温升速率先迅速升高再逐渐降低，其原因是蓄热初期温差较大，导致传热量较大，传热速率较快，随着蓄热的进行，蓄热单元平均温度逐渐升高，与电热丝的温差减小，根据传热学理论，蓄热单元与电热丝的辐射换热减弱.

图6 蓄热单元平均温度及温升速率随蓄热时间的变化

3.4 空气换热量及出口空气温度的比较

φ=qmCp(t″f-t′f)

(8)

式中：qm为空气的质量流量；Cp为空气的比热容；t′f、t″f分别为通风孔道进、出口空气温度.

图7、8分别为不同结构蓄热单元的空气换热量、出口空气温度随蓄热时间的变化.不同结构蓄热单元的空气换热量与出口空气温度随时间的变化具有一致性.在蓄热约7 200 s前，模型1的空气换热量和出口空气温度略高于其他3种结构蓄热单元，这是因为模型1受热量堆积的影响较大，靠近电热丝通道区域的温度高于另外3种结构的蓄热单元，与空气的换热较强.随着时间的推移，添加矩形孔道蓄热单元的空气换热量和出口空气温度开始逐渐高于模型1，并且随着矩形孔道宽高比增加，这种差距逐渐增大，原因是添加矩形孔道的蓄热单元因换热面积增加所带来的换热增强效果抵消了模型1因电热丝通道区域的温度较高所带来的换热增强效果.

图7 空气换热量随蓄热时间的变化

图8 出口空气温度随蓄热时间的变化

4 释热数值模拟结果与分析

4.1 不同结构蓄热单元温度场的比较

释热结束时刻，不同结构蓄热单元截面(z=0.225 m)温度场如图9所示.

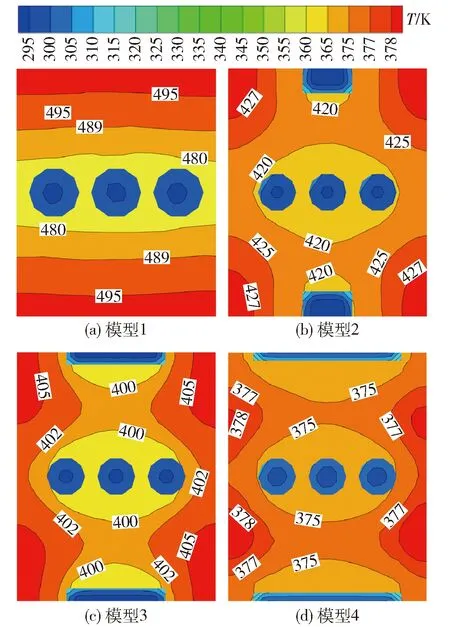
图9 蓄热单元截面(z=0.225 m)温度分布云图(释热结束)

从温度分布云图可以看出，靠近通风孔道的区域温度较低，随着与通风孔道的距离增加，温度逐渐升高.模型1的最高温度为495 K，模型4的最高温度为378 K，模型1、2、3、4的最高温度与最低温度之间的差值分别为15、7、5、3 ℃.即添加矩形孔道能够有效减小蓄热单元内部温度分布的不均匀性，并且有利于蓄热单元内部热量的充分释放.

4.2 蓄热单元平均温度及温降速率的比较

图10、11分别为在进口空气流速v=1.5 m/s，不同结构蓄热单元平均温度和温降速率随释热时间的变化.

由图10、11可知，在释热结束时刻，模型1的平均温度最高，达到488 K，模型4的平均温度最低，为376 K，在添加矩形孔道后，蓄热单元平均温度下降速度加快，矩形孔道宽高比越大，对应的温降速率越大.原因是在释热过程中，蓄热单元平均温度不断降低，蓄热单元与换热介质的换热温差减小，传热速率降低，并且矩形孔道宽高比越大，换热介质与蓄热单元的传热面积越大，相同时间释放的热量越多，蓄热单元的温度降低越快.在释热0～36 000 s，模型1的温降速率最低，之后模型1的温降速率开始高于其他3种模型，这是由于模型1的平均温度与换热介质的温差较高，抵消了其他3种结构蓄热单元因换热面积增加所带来的换热增强效果.

图10 蓄热单元平均温度随释热时间的变化

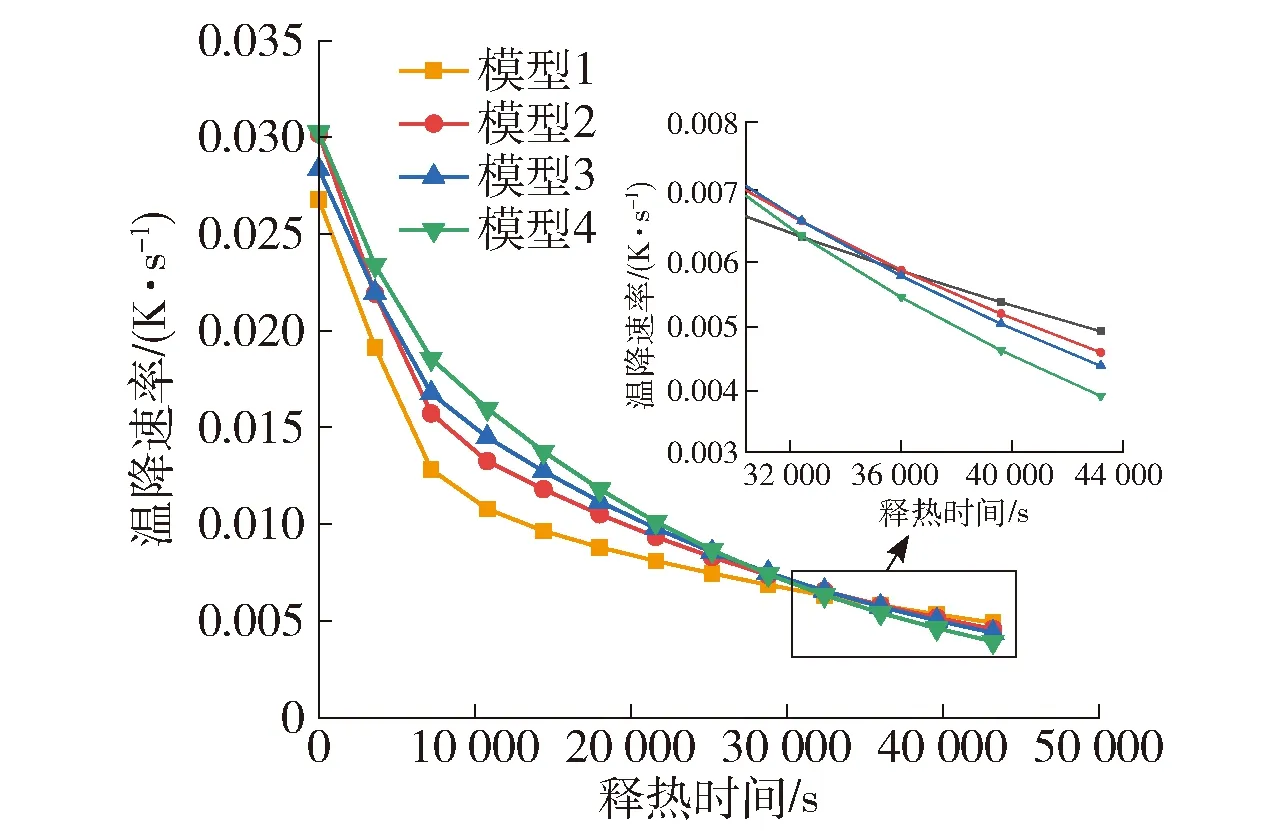
图11 蓄热单元温降速率随释热时间的变化

4.3 不同结构蓄热单元空气换热量的比较

图12为在进口空气流速为1.5 m/s，不同结构蓄热单元的空气换热量随释热时间的变化.不同结构蓄热单元的空气换热量随释热时间的变化趋势一致，随着释热时间的增加，4种结构蓄热单元的空气换热量的差别逐渐增大，释热约25 000 s，不同结构蓄热单元的空气换热量之间的差值基本达到稳定.到释热结束时刻，矩形孔道宽高比为18∶1的模型4的空气换热量最多，达到39 108 kJ，比不加矩形孔道的模型1的空气换热量多了22%，这是因为在保持通风孔道总横截面积一定的情况下，添加矩形孔道后，孔道的当量直径减小，表面传热系数提高，空气与蓄热单元的换热增强.

图12 蓄热单元空气换热量随释热时间的变化

4.4 进口空气流速对不同结构蓄热单元的影响

图13为不同结构蓄热单元平均温度降低到323 K所需的释热时间随不同进口空气流速的变化.从图13可以看出，同一蓄热单元，随着进口空气流速的增加，蓄热单元平均温度降低到323 K所需要的释热时间变短.释热时间的主要影响因素是由蓄热单元内部的导热热阻和传热介质空气与蓄热单元之间的换热热阻决定的，随着空气流速增大，传热介质空气与蓄热单元之间的对流换热系数增大，换热热阻减小，传热能力增强；不同结构蓄热单元平均温度降低到323 K所需要的释热时间随矩形孔道宽高比减小而增大，在进口流速为1.5 m/s，模型1释热33.5 h，模型4释热18.2 h；在满足释热12 h的条件下，模型1、2、3、4的平均温度降低到323 K所需设置的进口空气流速分别约为7、5、4、3 m/s，即在蓄热砖上添加矩形孔道可以显著降低风机的配置功率.

图13 蓄热单元释热时间随不同进口空气流速的变化

5 结论

本文结合工程实际中的蓄热砖结构，基于流固耦合换热理论，将流固界面处难以确定的热流边界条件转化为内部边界，建立了固体蓄热单元的流固耦合传热模型，模拟研究了蓄热砖孔道结构和进口空气流速等参数对蓄热单元蓄/释热性能的影响，通过对蓄热和释热的模拟结果比较分析得到以下结论：

1) 在蓄热过程中，蓄热单元的温升速率先升高再降低，添加矩形孔道的蓄热单元的平均温度降低，但与空气的换热量增多，随着矩形宽高比增大，这种差距更加明显.

2) 在释热过程中，蓄热单元的平均温度和温降速率随时间不断降低，添加矩形孔道，蓄热单元与空气的换热量增加.释热结束时，矩形孔道宽高比为18∶1的模型4的空气换热量达到39 108 kJ，比不加矩形孔道的模型1的空气换热量多了22%.

3) 结合不同结构蓄热单元的温度分布云图，在蓄/释热过程中，随着矩形孔道宽高比从2∶1增大到18∶1，蓄热过程的局部高温值由870 K降低到857 K，释热过程中最高温度与最低温度的温差由7 ℃降低到3 ℃，即随着矩形孔道宽高比增加，蓄热单元的局部高温值越低，温度分布的均匀性越好.

4) 在释热过程中，进口空气流速和矩形孔道宽高比越小时，释热速度越慢，所需释热时间越长.当进口空气流速为1.5 m/s时，模型1释热33.5 h，模型4释热18.2 h.