大宽高比弧形钢闸门流激振动数值分析
2022-05-16彭思贤赵兰浩
彭思贤,赵兰浩,毛 佳
(河海大学水利水电学院,江苏 南京 210098)
21世纪以来,我国对水环境和生态的要求日益提高,跨度较大、水头较低的大宽高比弧形闸门不断涌现[1]。但此类闸门结构刚度弱,动水启闭时易产生强烈振动,同时水动力荷载作用形式复杂各异,诱发的结构强烈振动也表现出不同的振型和性质[2]。闸门的流激振动按激励机制一般分为3种:外部诱发振动(EIE)、水流稳定性差异导致的振动(IIE)与结构自身相关的自激振动(MIE)[3-4]。总体而言,振动的主要原因是动水作用的不均衡[5-7]。目前,闸门振动特性的主要研究方法有原型观测、模型试验、数值模拟或模型试验与数值模拟相结合。胡木生等[8]利用原型观测的方法较为准确地测量出闸门的振动响应,蒋寅军等[9]用完全水弹性模型试验得到闸门不同开度下的动力响应,赵兰浩等[10]提出基于模型试验的物理模型-数学模型相结合的闸门流激振动计算方法,但研究的弧形闸门宽高比较小均在0.4~1.0之间,同时原型观测无法对待建闸门研究,完全水弹性模型较难实现,数值模拟在现有技术下缺乏一定精度[11-12],其他有关大跨度、宽高比大于3∶1的弧形闸门动力特性研究也较少[13]。
本文以闸门跨度为25.96 m,宽高比约为3.05的某节制闸为研究对象,该闸属于低水头大宽高比闸门,支臂支承桁架部位易发生失稳破坏[14-16]。针对闸门主体与易失稳的支臂部位,分别计算闸门有、无水体状态下的自振特性,研究不同支臂设计厚度对结构振频的影响,采用试验结合数值模拟的方法,将模型试验测得的脉动压力转化为节点荷载施加在数值模型上,通过随机振动方法得到该闸门的流激振动响应,可对类似大宽高比闸门结构的设计与安全运行提供参考。
1 计算方法
1.1 闸门自振特性
闸门结构的运动方程为
(1)

实际工程中,可忽略阻尼影响,假定结构做δ=φcosωt的简谐运动,得到闸门结构不考虑水体作用且忽略阻尼的自由振动方程:
Kδ=ω2Mφ
(2)
式中:ω为闸门自振频率;φ为闸门结构中各节点的振幅,不全为零。
考虑水体与结构作用情况下,当不可压缩流体做小振幅运动时,附加水压力(动水压力)p的变化服从拉普拉斯方程:
(3)
Hp-F=0
(4)
式中:H为劲度矩阵H=∑He;F为节点荷载F=∑Fse。边界决定于固体的移动,固体边界在法线方向的位移分量用适当的形函数以及节点位移表示,可推导得
(5)
设动水压力荷载为Rp,Rp=∑GTpse,式中pse为流体压力,G为流体压力的形函数在流体与固体接触面上的积分,将式(5)代入可得
(6)
其中Mp=GTH-1G
式(2)中增加附加水体质量矩阵Mp,即得到考虑水体与结构作用的振动方程:
Kδ=ω2(Mp+M)φ
(7)
1.2 脉动压力频谱分析方法
假设各测点的脉动压力P(t)是平稳各态历经随机变量,节点i上的节点荷载可由绕节点周围的小块面积叠加得来,即:
(8)
节点荷载的相关矩阵为:RF(τ)=E(F(t)F(t+τ)T),两端作傅里叶变换可得节点i、j间的节点荷载功率谱矩阵:
(9)
其中SPikPjm(ω0)=γPikPjm(ω0)
式中:SPikPjm(ω0)为小块面积Aik和Ajm上任意两点之间的互谱密度;Aik、Ajm为测点k对节点i、j的影响面积;lik、ljm为影响面积Aik、Ajm的法线方向向量。
设γij=γxijγyijγzij,γij为相干函数,并记:γij=A(ω0)-i0B(ω0)。以x方向为例,γij(ω0)可表示为负指数衰减函数的形式:
γij=exp(-k1|xi-xj|)exp[-i0ω0k2(xi-xj)]
(10)

γij=γxijγyijγzij=exp(A)cos(Bω0)+
i0exp(A)sin(Bω0)
(11)
其中A=-(k0x1|xi-xj|+k0y1|yi-yj|+
k0z1|zi-zj|)
B=-(k0x2|xi-xj|+k0y2|yi-yj|+
k0z2|zi-zj|)
y、z方向同理可得。
1.3 随机振动方法
将考虑水体与闸门之间耦合作用下最低p0阶振型φ=(φ1,φ2,…,φp0)和相应频率ω=(ω1,ω2,…,ωp0)T振型展开,位移向量δ写成广义坐标Y的函数δ=φY,代入式(1),并左乘φT,可得
(12)

式中:H(ω)为传递函数矩阵;SF(ω)为节点荷载功率谱矩阵。
对式(13)积分可得到位移响应均方根值:
(14)
用弹性矩阵DG与应变矩阵B求得应力响应均方根值σ:
σ=DGBδ
(15)
2 水力学模型试验
某节制闸设双主横梁,为开敞式平底板整体结构,支臂为三角直支臂结构,支臂断面为工字形组合,底板顶面高程为1.00 m,底板总厚度为2.50 m,闸墩顶高程为10.30 m,闸门门叶尺寸25.96 m×8.50 m(宽×高),面板弧长9.05 m,面板弧面半径8.50 m,闸门上游汛期限水位8.50 m,灌溉设计水位9.0 m,校核水位9.50 m。
2.1 脉动压力测点布置与试验工况
试验主要测量闸门在不同典型水位(8.50 m、9.0 m、9.50 m),不同开度(10%、20%、40%、50%、60%)下各测点的脉动压力,闸门局部开启时为孔口出流。模型采用PVC材料制成,几何比尺为1∶25,满足Froude相似条件。共布置11个测点,闸门结构与测点布置如图1所示。

图1 闸门结构及测点布置示意图(单位:mm)
2.2 脉动压力频谱分析
试验表明,闸门局部开启时,脉动压力与水流紊动程度有关,面板底部测点1处流速较大、水流紊动程度高,此处脉动压力试验值最大,各测点脉动压力优势频率主要集中在4~12 Hz。由于测点工况较多,图2、表1只给出闸门在上游水位8.50 m,开度10%时典型测点1、4的脉动压力时程曲线、功率谱线与上游水位9.50 m,不同开度下典型测点1、4、6脉动压力均方根值和优势频率。
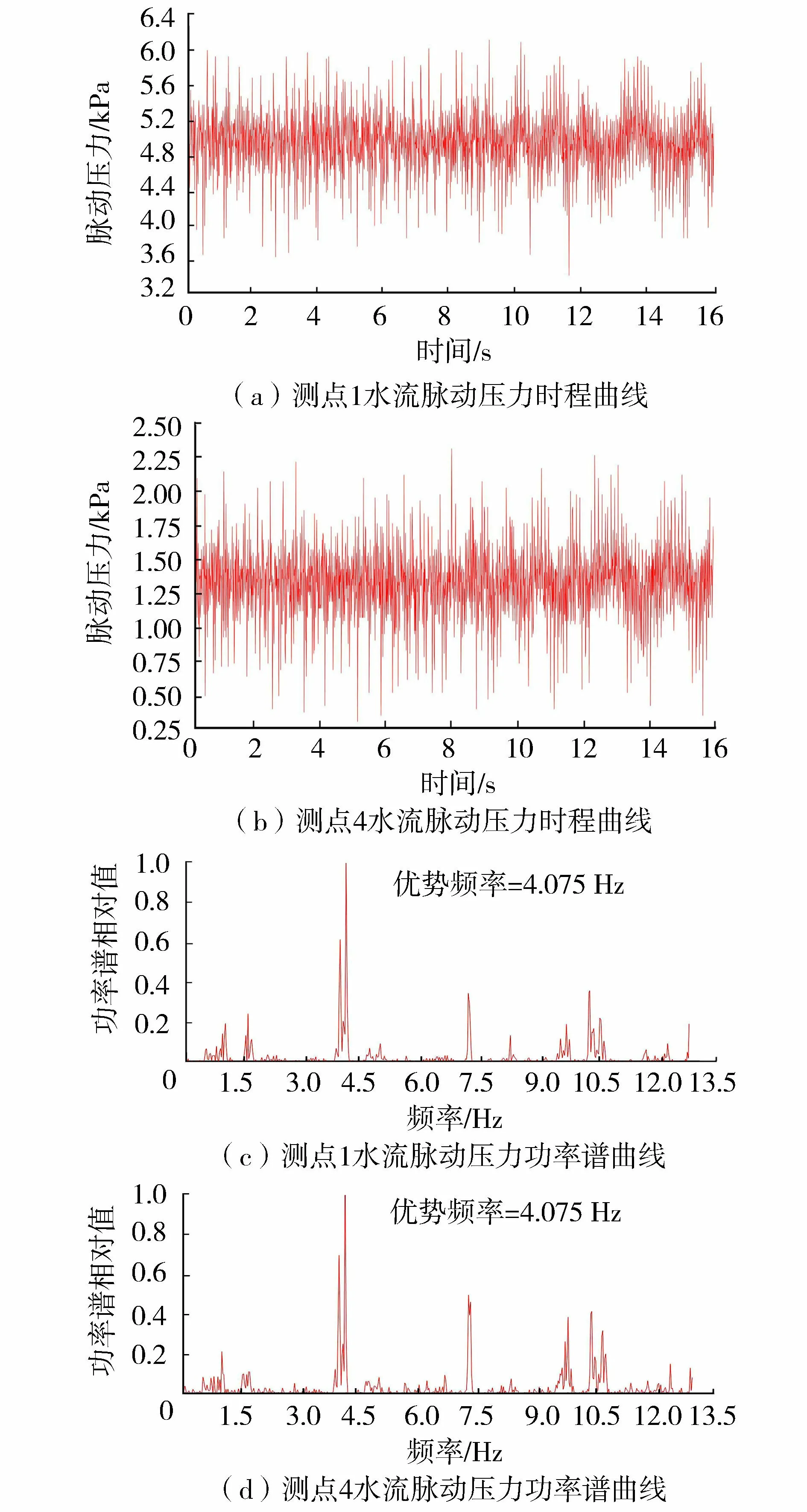
图2 典型测点1、4水流脉动压力时程曲线与功率谱曲线
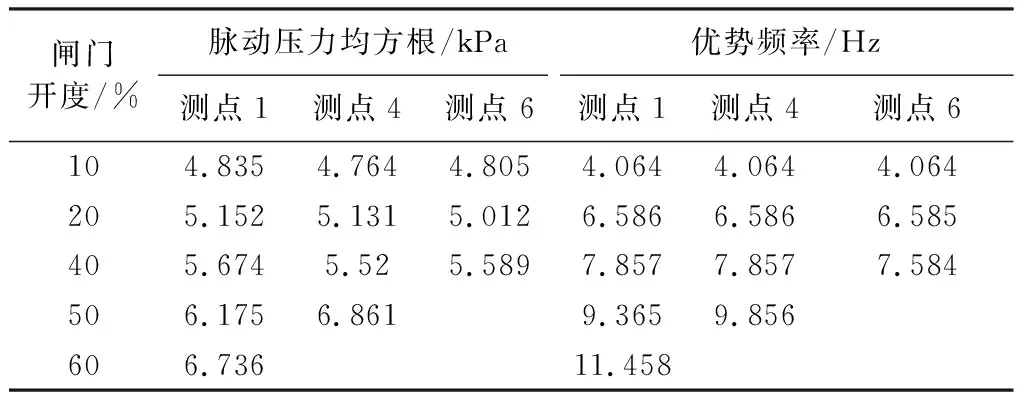
表1 9.50 m水位不同开度下测点1、4、6脉动压力
a.由图2可看出测点1和4的脉动压力时程曲线呈现正弦波形,测点1的脉动压力试验值明显大于测点4处。功率谱曲线可知两测点频率范围均在0~13.5 Hz,优势频率均为4.075 Hz。
b.分析表1可知,上游水位一定,闸门开度增大,脉动压力的均方根值与优势频率均呈增大趋势,均方根值增幅逐渐增加,水流脉动程度显著增强。
3 数值模拟分析
3.1 闸门有限元模型参数
取x轴正向与水流方向相反,y轴垂直水流方向指向河流的左岸,z轴垂直指向上方。水体区域计算时取为自闸门底缘向上游延伸至闸门高度的10倍左右[17]。闸门面板、主横梁、纵隔板以及支臂部位采用四边形板壳单元模拟;启闭杆采用杆单元模拟;支座部位采用八节点六面体单元模拟。计算模型的节点总数124 441,单元总数120 176,其中八节点实体单元总数20 064,四节点面单元总数99 472,三节点面单元总数432,杆单元总数208。
材料参数:闸门门体主要采用Q345钢,密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.296 3。水体的密度1 000 kg/m3,重力加速度为9.81 m/s2。闸门与水体的有限元模型如图3、4所示。

图3 弧形钢闸门有限元模型

图4 水体有限元模型
约束条件:挡水工况,闸门面板底部设置z向约束,支座底端设置固定约束,转轴设置x向约束;起吊工况,启闭杆一端设置固定约束,支座底端设置固定约束,转轴设置y向约束。
3.2 流固耦合对自振特性影响
表 2为闸门在挡水工况与起吊工况下,考虑流固耦合(有水状态)与不考虑流固耦合(无水状态)时的前十阶自振频率,表3为起吊工况闸门有水与无水状态下的前六阶振型。
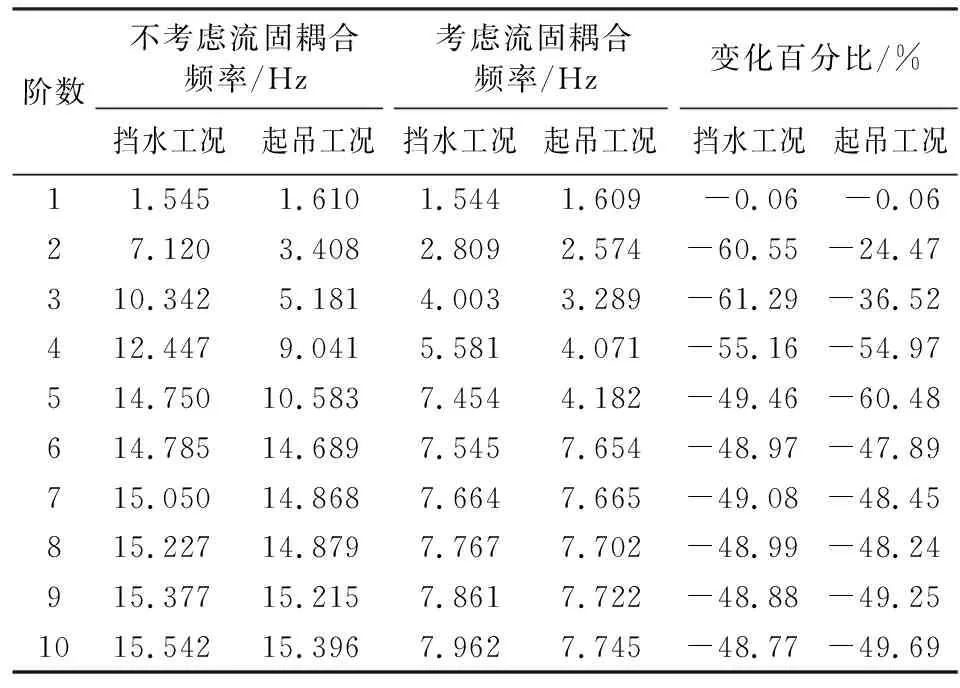
表2 自振频率计算结果

表3 起吊工况典型阶数振型情况
由图5与表2和表3数据可知:①闸门一阶振型各工况均表现为闸门面板的横河向运动,顺水流方向与水体无作用,因此流固耦合作用对闸门基阶振频的影响较小,基频较无水体作用只降低了0.06%左右。②流固耦合对自振频率的影响是非线性的,高阶振频因水体作用而显著降低,挡水工况振频最高降幅出现在第三阶,降低61.29%,起吊工况则出现在第五阶,振频最多降低60.48%。流固耦合作用改变了闸门二阶之后的振动形式,其中对三至五阶的振型影响较为显著。③第六阶及更高阶的振型主要表现为面板中部门叶局部的扭曲变形和门叶后主梁腹板局部的弯曲变形,闸门主体钢结构与桁架结构无明显变形,高阶振型主要影响闸门面板的局部结构,对闸门整体结构无太大影响,而低阶振型易引起闸门整体结构的振动变形,是影响闸门安全运行的重要因素。

图5 设计水位挡水工况下闸门一阶、六阶振型
3.3 支臂截面厚度对闸门振频影响
为研究闸门在不同支臂截面厚度下的自振频率,选取闸门挡水(无水)工况与起吊有水工况,计算支臂厚度增加30%下的闸门振频与原振频对比。
由表4可知:①支臂截面厚度增加,闸门振频随之增大,无水状态基频最大增幅5.50%,有水状态基频最大增幅10.69%。②支臂截面厚度的改变对高阶振频影响较小,主要由于支臂截面变大,闸门结构刚度增大,而闸门高阶振动形式主要表现为闸门面板与主梁腹板的局部扭曲变形,支臂无明显运动,因此支臂对闸门高阶振频影响较小。

表4 闸门闭合无水、起吊有水工况支臂厚度的自振特性
3.4 闸门流激振动应力响应
将典型水位不同开度的脉动压力作为节点荷载,通过数值计算得到结构的应力响应。由表5、表6可以看出:①在脉动压力作用下,闸门在9.50 m水位下10%开度与20%开度时的整体应力水平较高。主要构件的应力以平面应力为主,弯曲应力与平面应力相比小很多,其影响几乎可忽略。②闸门应力主要集中在结构中下部,上部结构应力水平较低。纵、横梁处应力最大,吊耳处应力最低。平面应力的最大值为60.805 MPa,出现在纵梁腹板底部。最大平面剪应力为9.969 MPa,出现在支臂腹板处。③这是由于在闸门上游水位9.50 m开度10%、20%时,闸门与水体直接接触范围较大,下泄水流的脉动荷载集中作用在闸门结构的中下部,梁格系与支臂应力水平较高,同时过闸流量与流速大,水流波动强烈,水动力作用显著,结构整体应力水平随之增大。
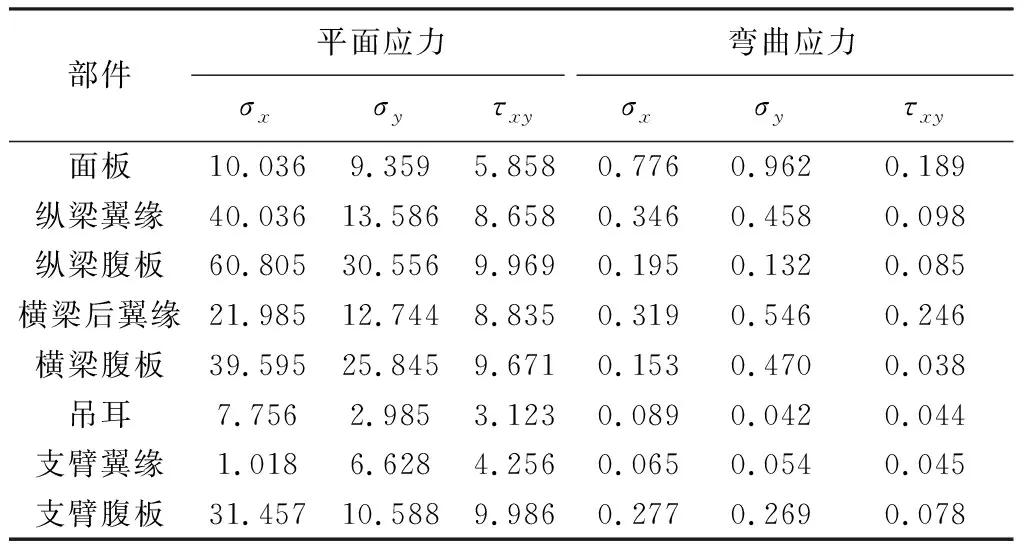
表5 所有工况闸门主要构件平面、弯曲应力最大值 单位:MPa
3.5 闸门流激振动位移响应
由表7可以看出:①闸门面板处位移最大,支臂处位移最小。在9.50 m水位闸门开度20%时,出现位移最大值,为x向位移4.029 mm,出现在纵梁腹板、纵梁翼缘与面板顶部相接处;y向最大位移为0.368 mm,出现在吊耳的顶端;z向最大位移为1.608 mm,出现在闸门横梁后翼缘的中间部位。②由于闸门底部受到底部支臂的支撑作用,x向位移较小,在上下支臂的支撑下,结构x向位移最大值一般都出现在闸门结构的顶部。支臂变形主要是由于脉动压力的作用下,发生横河向和垂直向的变形,一般y向和z向位移较大。

表7 所有工况闸门主要构件位移最大值及所在工况
4 闸门动力响应评价
目前对于闸门动力响应的评价并无标准[18],本文采用动力系数法即将动静应力之和与静应力的比值范围作为安全指标,动力系数低于1.20则闸门的动力响应不会对闸门正常运行产生危害。由表8可知,闸门各构件动力系数均低于1.20,其中纵梁腹板处动应力最大达到61.247 MPa,相应动力系数1.172,闸门动力系数满足抗振设计要求[19],因此脉动水压不会对正常运行的闸门造成失稳破坏。

表8 所有工况闸门主要构件最大动、静应力与动力系数
5 结 论
a.闸门基频与脉动压力主频范围相差较大,与优势频率相差60%以上,理论上发生共振可能性很低,闸门各部位动力系数均低于1.20,动力响应不会对闸门正常运行造成危害。但闸门在上游水位9.00 m开度40%与水位9.50 m开度10%、20%时动应力与动位移响应较大,实际运行时应注意此工况下闸门的动力安全。
b.当弧形闸门宽高比大于3∶1,由于结构尺寸、跨度较大,约束刚度相对较弱,自振基频较小,中小开度运行时易在水流脉动作用下发生强烈振动。
c.闸门水头低而跨度大,宽高相差悬殊,结构抗扭刚度弱,支臂在低阶振动时易发生扭曲变形。支臂截面厚度主要影响闸门低阶振频,对高阶振频无太大影响,因而在类似大宽高比弧形闸门的支臂结构设计阶段需合理增加支臂刚度,防止支臂部位发生动力失稳破坏。
