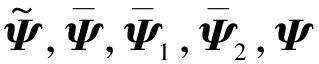考虑弹性地基的正交双曲蜂窝夹层壳体自由振动分析

倪 臻，李旦望，夏 烨，周 凯，华宏星

(1.中国航发商用航空发动机有限责任公司，上海 200241；2.上海交通大学 振动冲击噪声研究所，上海 200240；3.上海交通大学 机械系统与振动国家重点实验室，上海 200240；4.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240)

蜂窝夹层壳由上下面板和蜂窝芯层组成，具有质量轻、强度高的特点，并有良好的隔音、减振特性，近年来越来越广泛地被运用于航空航天、车辆、船舶等领域。然而，蜂窝夹层壳体往往会受到复杂的环境激励，进而产生振动，并最终疲劳破坏。因此，有必要建立可靠的动力学模型以研究蜂窝夹层壳体在外激励下的振动响应。

杨稳等[1]指出，由于蜂窝夹层材料具有离散非均匀的特性，直接对其进行建模分析需要消耗巨大的时间和计算成本。为此，大量学者对蜂窝芯层的等效方法进行了研究，将其作为各向异性材料进行建模[2-6]。基于蜂窝芯层等效方法，Eipakchi等[7]利用经典板壳理论建立了具有负泊松比的圆柱壳模型，并计算了其在压力载荷下的动力学响应。Duc等[8]基于一阶剪切变形理论，获得了具有负泊松比蜂窝结构的圆柱壳体动力学响应特性。王盛春等[9]基于Reissner-Mindlin理论，得到了考虑剪切变形的四边简支矩形蜂窝夹层板弯曲振动固有频率的精确解。Zhang等[10]利用一阶剪切变形理论，研究了悬臂三明治蜂窝夹层板的自由振动及非线性响应特性。Li等[11]基于三阶剪切变形理论计算了蜂窝夹层板的弯曲振动特性。Yu等[12]采用经典板理论、一阶剪切变形理论和三阶剪切变形理论建立了蜂窝夹层板的动力学模型，并对采用3种不同模型得到的固有频率进行了比较。他们指出，经典板理论与一阶剪切变形理论在计算蜂窝夹层板的振动特性时具有较大的计算误差。Liu等[13]对此现象进行了分析，认为采用低阶剪切变形理论会高估夹层壳体上下面板的剪切应力，并提出了针对一阶剪切变形理论的改进办法。Sun等[14]利用有限元法计算三明治蜂窝夹层板在冲击载荷下的响应，并通过试验验证了计算结果。王威远等[15]对锥形复合材料蜂窝壳的振动传递特性进行了试验研究。

值得一提的是，尽管关于蜂窝夹层板壳的研究较多，但大多集中在蜂窝夹层平板或圆柱壳、圆锥壳等简单形状壳体的动力学建模和分析上，且并未考虑弹性支承约束。因此，亟需对具有弹性支撑约束的复杂形状蜂窝夹层壳体的动力学特性开展研究。为能考虑中厚蜂窝壳体的振动响应特性，本文将基于一阶剪切变形理论和修正的Gibson公式建立考虑弹性地基的双曲蜂窝夹层壳体控制方程，并对其自由振动特性进行分析。

1 理论模型

1.1 运动学及动力学关系

双曲蜂窝夹层壳体的结构示意图，如图1所示。图1中：hc为峰窝芯层厚度；h为壳体总厚度。蜂窝夹层壳体是由上下面板及蜂窝芯层组成的空间三维结构。壳上任意一点的空间坐标可由其中面几何形状及对应的厚度表示。对正交双曲壳体，其中面可用参数方程r=r(ξ1,ξ2)表示，其中:r为壳体中面的参数方程；ξ1和ξ2为曲面的正交广义坐标，其取值范围为ξ10≤ξ1≤ξ1L，ξ20≤ξ2≤ξ2L。在给定了壳体中面几何后，壳体上任意一点的空间位置即可由正交参数坐标(ξ1,ξ2,ζ3)进行表示。其中，ζ3为壳上一点到壳体中面的有向距离，其正向为r(ξ1,ξ2)定义的壳体曲面法线方向。

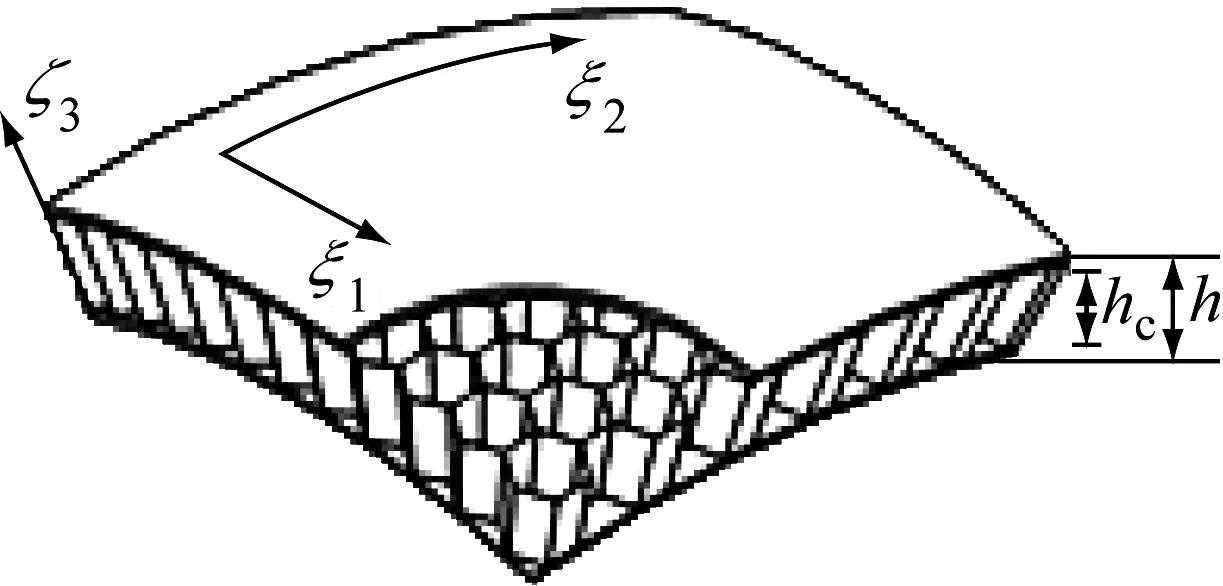
图1 双曲蜂窝夹层壳体

为了考虑壳体剪切变形和转动惯量对系统动力学特性的影响，可以采用一阶剪切变形理论给出壳体在曲面坐标下的位移场表达式

(1)

式中:u1,u2,u3分别为壳体上任意一点沿ξ1，ξ2，ζ3方向的位移；t为时间；u0，v0和w0为壳体中面上一点的位移；φ1和φ2为剪切转角。

壳体的线性应变位移关系可以通过三维小变形理论得到[16]

(2)

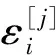
蜂窝芯层及面板的应力应变关系由文献[17]给出

(3)

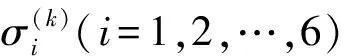
(4)

其中

(5)

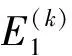
(6)

蜂窝芯层一般为由各向同性材料制备而成的六边形周期结构，其中的单个胞元如图2所示。图2中:蜂窝胞元的壁厚为tc；壁长分别为l1c和l2c;蜂窝胞元壁的斜边角度为θc。此类蜂窝结构可等效为正交各向异性材料，其等效参数由改进的Gibson公式给出

图2 蜂窝胞元

(7)

式中：Ec,Gc和ρc分别为蜂窝芯层所用材料的弹性模量、剪切模量和密度；ρ(2)为蜂窝芯层等效密度；η1=l2c/l1c，η2=tc/l1c。

1.2 蜂窝夹层壳体能量方程

蜂窝夹层壳体的动能表达式为

(8)

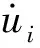
a1a2dξ1dξ2

(9)

式中：δ为变分符号；a1和a2分别为ξ1和ξ2方向的拉梅系数；Ii为考虑了曲率之后的第i阶惯性矩(i=1,2,3)

(10)

壳体的应变能表达式为

(11)

式中，σij和εij分别为壳体应力场和应变场。将式(2)和式(3)代入式(11)并取变分，可以得到

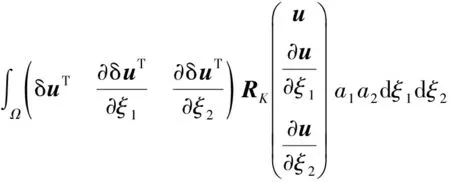
(12)

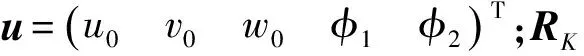
考虑壳体边界及弹性地基所做虚功，其表达式为沿边界方向的线积分

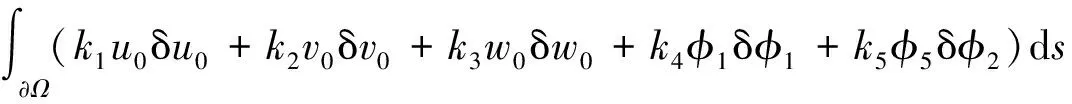
(13)

式中：k1，k2和k3为沿u，v和w方向的平动刚度；k4和k5为沿φ1和φ2方向的转动刚度。弹性地基所做虚功[18]为

(14)

式中，ke为弹性地基刚度。

系统的总虚功为边界条件和弹性地基所做的虚功的叠加，即有

δV=δVBC+δVe

(15)

1.3 基于改进傅里叶法的壳体振动求解

对任意边界条件下的壳体，可以采用改进傅里叶法[19]进行求解。将壳体位移场利用傅里叶级数进行展开

(16)

式中：Umn(t)，Vmn(t)，Wmn(t)，Φ1mn(t)和Φ2mn(t)均为壳体位移的广义坐标；U0(t),V0(t)，W0(t),Φ1(t)和Φ2(t)分别为其对应的向量形式；φm(ξ1)和ψn(ξ2)分别为对应ξ1和ξ2的傅里叶基函数;Ψ(ξ1,ξ2)为傅里叶基函数对应的向量形式；M和N分别为对应基函数的阶次。φn和ψn的表达式分别为

(17)

(18)

将式(16)代入哈密顿原理表达式

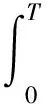
(19)

即可得到如下矩阵方程

(20)

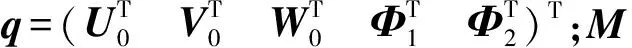
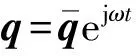
(21)

2 数值分析及讨论

2.1 收敛性分析及方法验证

为了验证给出方法的可靠性，首先建立一含蜂窝芯层的壳体模型。壳体的曲面参数方程为

r=[ξ1,f(ξ1)sinξ2,f(ξ1)cosξ2]

(22)

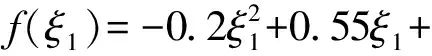
首先对模型的收敛性进行验证。分别采用本文给出的方法和商用有限元软件ABAQUS建立蜂窝夹层壳体模型。在采用有限元法进行建模时，采用的单元类型为二阶减缩积分四边形壳体单元S8R，建立的网格总数为2 120，如图3所示。当选取不同阶次基函数时，四边简支的蜂窝壳固有频率及其与有限元结果的比较，如表1所示。从表1可知，采用本文给出的方法计算得到的系统固有频率与有限元法计算得到的结果吻合良好。采用两种方法计算得到的系统振型，如表2所示。从表2可知，本文给出的方法亦能够准确计算蜂窝壳的振型。表1还给出了采用不同方法所消耗的计算时间。从结果可知，由于推导得到了壳体的半解析解，此方法具有很高的计算效率。

图3 壳体有限元模型

表1 不同阶次基函数系统的固有频率

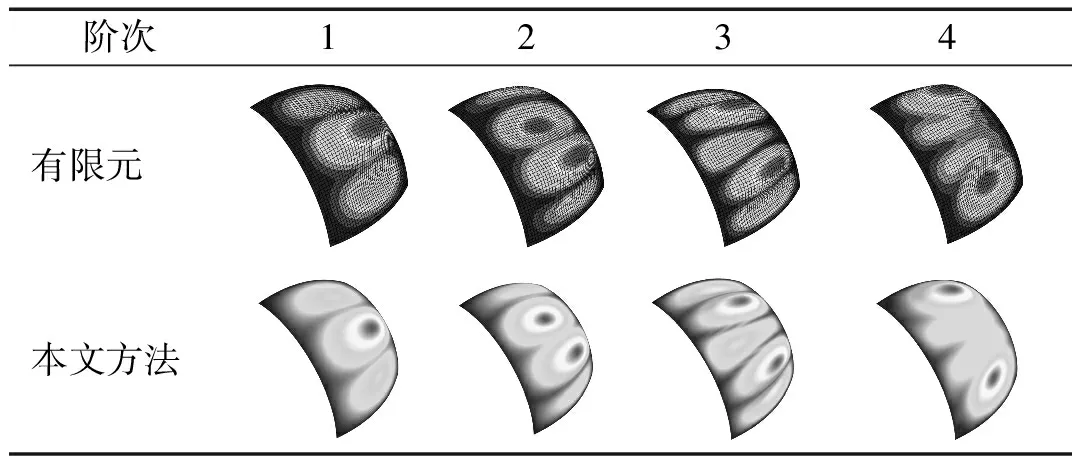
表2 壳体振型对比

接下来考虑弹性地基对系统固有频率的影响。壳体在不同地基刚度下的前4阶固有频率，如图4所示。从图4可知，当地基刚度值小于1×106Pa/m时，系统的固有频率随地基弹性的变化并不明显。而当地基刚度值大于1×109Pa/m时，其固有频率也趋于定值。当地基刚度值在106～109Pa/m时，系统的固有频率随地基弹性地增大而迅速增大。这是由于弹性地基的引入约束了壳体沿中面法向的运动，从而提高了系统的刚性，因此在考虑了弹性地基后，壳体的固有频率有了显著地提高。当地基弹性达到1×109Pa/m时，地基可以认为是刚性的，因此此时继续增大地基刚度不会影响系统的固有频率。而当地基弹性小于1×106Pa/m时，由于其刚度值较小，地基并不会对系统的动力学特性产生显著影响。因此，此时系统的固有频率随地基弹性的变化并不明显。

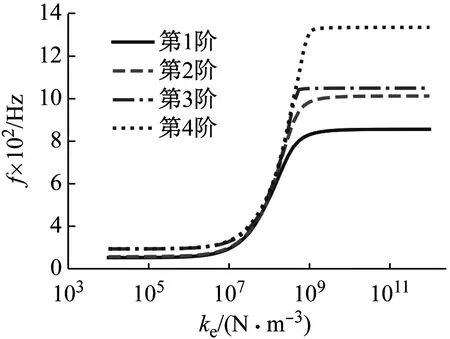
图4 固有频率随弹性地基刚度的变化

2.2 参数分析

2.2.1 芯层厚度比

改变蜂窝夹层壳的结构参数，讨论芯层厚度比对系统固有频率的影响。保持壳体的总厚度h=20 mm为定值，改变蜂窝夹层壳的厚度比η=hc/h。当地基刚度分别为0，2×108Pa/m和2×109Pa/m时，系统的前4阶固有频率随厚度比的变化关系，如图5所示。从图5可知:当ke=0时，系统的固有频率随η地增大而减小;且随着η的增大，系统固有频率的下降速度也逐渐增大;当ke=2×108Pa/m时，系统的固有频率首先随厚度比的增大而升高;但随着厚度比继续增大，系统固有频率开始迅速下降;类似的，当ke=2×109Pa/m时，系统的固有频率随厚度比地增大而先增大后减小。

(a)ke=0

事实上，系统的固有频率取决于模态坐标下系统各阶刚度与质量的比值。系统的模态质量越大，则对应模态的固有频率越低；系统的模态刚度越大，则对应模态的固有频率越高。在本算例中，增大蜂窝厚度比会同时减小系统的刚度和质量。因此，系统固有频率的变化情况取决于模态质量与模态刚度随蜂窝厚度比的相对变化情况。对于蜂窝夹层壳体，由于其芯层较软，因此其刚度主要由上下面板提供。当芯层厚度比较小时，系统固有频率随厚度比的变化方向取决于地基刚度的大小。然而，随着芯层厚度比地增大，其上下面板的厚度逐渐减小，面板对系统总体刚度的贡献急剧下降，使得壳体总体刚度迅速减小。此时，无论地基刚度取为何值，系统固有频率均会迅速降低。

2.2.2 蜂窝胞壁参数

六边形蜂窝结构具有两个重要的无量纲参数η1，η2，分别为六边形蜂窝结构的边长比和蜂窝壁厚比。为了分析其对系统动力学特性的影响，系统的前4阶固有频率随η1和η2的变化关系，如图6所示。在进行计算时，弹性地基刚度取为ke=2×108Pa/m。从图6可知，改变η1对系统固有频率的影响并不显著。当η2较小时，增大η1会使得系统的固有频率略有上升；而当η2较大时，增大η1则可能会降低系统的固有频率。但是，系统的固有频率会随η2地增大而显著降低。这表明，增大蜂窝壁厚会显著增大壳体的总质量，但是对系统刚度的影响并不明显。因此，增大蜂窝壁厚会降低系统的固有频率。

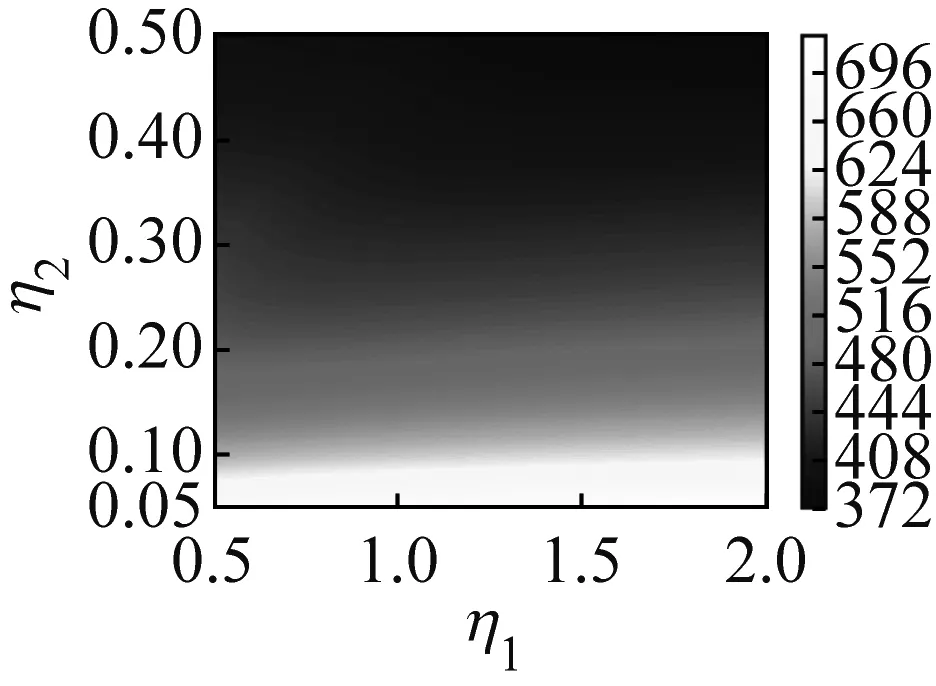
(a)第1阶

2.2.3 胞元角度及铺层方向

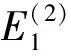
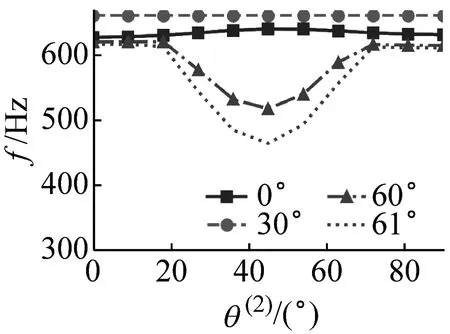
(a)第1阶

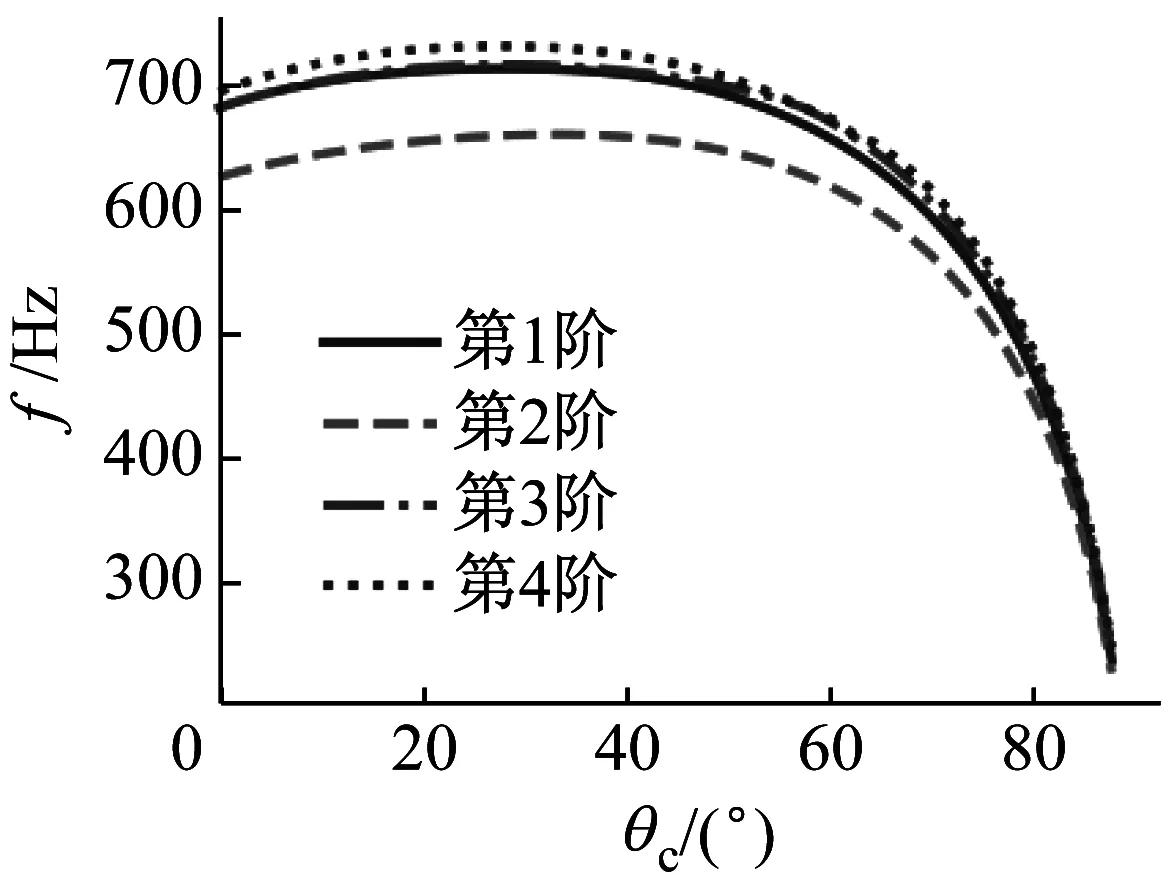
图8 固有频率随θc的变化关系

3 结 论

针对具有弹性地基的复杂形状蜂窝夹层壳体，通过一阶剪切变形理论和改进的Gibson公式建立了系统的能量泛函，并利用哈密顿原理给出了其控制方程。利用改进傅里叶法对控制方程进行求解，并通过数值算例验证此方法的快速性和可靠性。随后，基于给出的模型，通过变参数计算揭示了蜂窝芯层各参数对系统动力学特性的影响规律。得到以下结论：

(1)当芯层厚度较小时，系统固有频率随芯层厚度比的变化关系取决于弹性地基刚度值的大小;当芯层厚度较大时，系统固有频率随芯层厚度比地增大而迅速降低。

(2)蜂窝胞元边长比对系统固有频率的影响并不明显，但是增大蜂窝壁厚会使得系统的固有频率显著降低。

(3)系统固有频率随胞元角度地增大而先升高后降低，且当胞元角度较大且铺层方向处于20°～60°时，其固有频率对胞元角度的变化具有极高的敏感性。

附录A

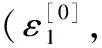
(A.1)

式中，T为位移-应变变换矩阵，将其展开有

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

附录B

考虑壳体曲率的刚度系数矩阵RK为

(B.1)

其中

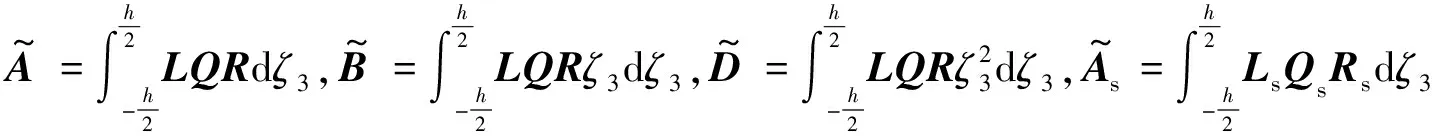
(B.2)

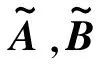
(B.3)

(B.4)

Κs为剪切修正因子，其表达式由文献[20]给出。

附录C

系统的广义质量矩阵M可以写为

(C.1)

其中

(C.2)

系统的广义刚度矩阵K可以写为

(C.3)

其中

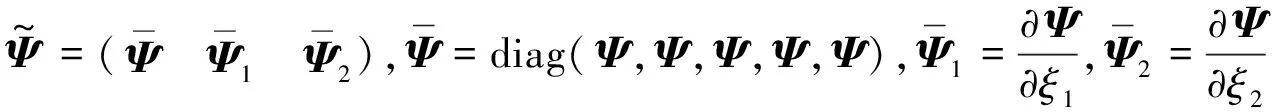
(C.4)