基于模糊PID的电子水泵在线检测流量控制研究

张雅琴,范伟军,,潘银斌,王 飞

(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.杭州沃镭智能科技股份有限公司,浙江 杭州 310018;3.瑞立集团瑞安汽车零部件有限公司,浙江 温州 325299)

汽车电子水泵作为国内新近开发的汽车零部件产品,其性能的在线检测是保证产品质量的重要环节。水泵性能在线检测要求进行多点流量的快速控制,检测系统通常采用控制调节阀的开度实现检测流量工况的切换,在检测过程中,流量的控制精度直接影响在线检测数据的准确度,流量控制调节时间直接影响检测生产的节拍。

在流量切换过程中,检测系统调节阀开度的变化会引起水泵进出口压降变化,介质状态易形成不稳定紊流;此外,管道内水流冲击等因素也会大大增加流量控制的难度,造成流量控制稳定误差大,稳流控制时间长,以至影响水泵检测效率。目前水泵性能测试一般采用传统PID法控制流量,PID控制参数依赖于调参人员的经验,流量调节时间长,无法满足非线性的在线检测系统对于控制速度的要求[1]。DUTTA针对开环流量控制系统提出了一种灰狼优化控制算法[2],该方法响应速度快,但无法满足电子水泵在线检测多流量点的闭环高精度控制要求。关于电子水泵在线检测流量切换的快速控制,SHAHID的模糊逻辑液位控制研究[3]和刘志壮等对控制阀模糊PID控制仿真研究[4]表明,模糊逻辑控制器有较好的稳定性和快速响应能力。

本文将在分析电子水泵性能检测系统基础上,构建检测系统数学模型,并设计模糊PID流量控制方法,以实现电子水泵性能在线检测流量的快速、稳定、高精度控制。

1 电子水泵测试流量控制需求

电子水泵性能测试项主要分为流量-扬程、流量-功率、流量-效率等,所有的性能检测项目都涉及到流量的控制。通过设置多个检测流量值,当系统水流量稳定至目标值时,采集当前测试管路的压力、电子水泵的电流等参数,计算扬程、效率和功率指标,并绘制对应的流量-扬程、流量-功率等性能曲线[5],实现电子水泵的性能检测。

基于上述检测项目设计的电子水泵性能在线检测系统如图1所示。该系统主要由电子水泵、压力传感器、流量计、调节阀、主水箱等构成,调节阀与流量计配合用于调节管路内的水流量。当流量值小于设定流量值时,增大调节阀开度,管道内阻力损失变小,流量增大;当流量值大于设定流量值时,减小调节阀开度,管道内阻力损失变大,流量减小。待到流量稳定在设定值时,相应的调节阀也稳定于某一开度,此时记录各传感器的示值,并进行各指标的计算。

图1 电子水泵性能在线测检测系统示意图Figure 1 Schematic diagram of electronic water pump performance test system

在流量控制的过程中,管路内介质受调节阀开度变化影响,变为不稳定的紊流,并在调节阀处产生局部水头损失,流量的变化呈非线性状态,流量控制难以快速稳定。此外,测试的流量点数多,流量设定值之间的跨度大等都影响着流量的调节时间。研究流量快速稳定的控制方法是减少检测时间与提高生产效率的关键。

根据某企业在线检测需求,电子水泵在线检测需检测至少8个不同流量值的性能,流量控制稳态误差±1%,单点流量进入稳态的控制节拍为120 s。

PID控制是水泵测试系统最常用的流量调节方式,它以系统误差为输入,利用比例、积分、微分计算出调节阀的输出量。图2为电子水泵检测系统采用常规PID实现100 L/min流量控制的响应曲线。

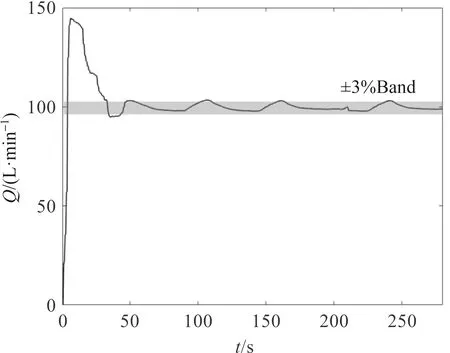
图2 系统流量PID响应曲线Figure 2 Experimental response curve of PID control

由图2可知,检测系统在240 s后,流量控制误差超过±3.0%,流量稳定控制时间大于240 s,不能满足电子水泵在线检测需求。因此基于模糊逻辑控制器的快速精确控制能力,研究电子水泵性能检测流量快速控制方法有重要的现实意义。

2 模糊PID控制器设计

模糊PID是在传统PID的基础上,利用模糊逻辑对控制参数进行优化,相比常规PID,模糊控制器具有实时调整参数并消除系统余差的优势。电子水泵在线性能检测流量模糊PID控制器设计如图3所示,该闭环反馈系统的Qs为设定流量值,e为系统流量误差,ec为误差变化率,Q为实际流量,Kp、Ki、Kd分别为经模糊控制器调整后的PID比例、积分、微分参数,x(Q)为调节阀阀门开度-流量模型,指流量稳定时调节阀的阀门开度与电子水泵性能检测系统管道内流量的关系式,xm为流量平衡状态下调节阀的理论开度,xf为调节阀的实际开度,G(s)为调节阀的传递函数,Q(x)为x(Q)的反函数[6]。

图3 电子水泵性能检测流量模糊PID控制框图Figure 3 Block diagram of fuzzy PID control in electronic water pump test system

由图3可知,流量模糊PID控制器设计主要包含x(Q)、G(s)与Q(x)等系统流量控制模型的设计,以及包含参数整定和建立模糊推理规则的模糊PID控制器主体设计等两部分。

2.1 电子水泵检测系统流量控制模型

电子水泵检测系统流量控制模型主要包括阀门开度-流量模型x(Q)、调节阀传递函数G(s)以及x(Q)的反函数Q(x)。

2.1.1 阀门开度-流量模型

调节阀是一个局部阻力可变的节流元件,流过调节阀的流量不仅与其开度x有关,还与阀门前后压差有关[7]。调节阀在设定开度x下的流通能力Cx满足以下关系

(1)

式(1)中,ΔPv为调节阀前后压差,Pa;Q为管道内流量,m3/s;ρ为液体密度,kg/m3。

为得到调节阀的阀门开度与管道内流量的关系式,需计算调节阀前后压差ΔPv与流量Q的关系式,以及调节阀的流通系数Cx与阀门开度x关系式。

在系统管路中,电子水泵与主水箱的作用等效于压源,管路和调节阀等其他元件等效为压阻,忽略管道和传感器的压力损失,闭合测试回路中调节阀压差ΔPv与其他元器件的压力关系为

ΔPp+ρgh=ΔPv。

(2)

式(2)中,ΔPp为水泵进出口压升,Pa;h为主水箱内液位高度,m;g为重力加速度,g=9.81 m/s2。

由式(2)可知,电子水泵进出口压升与主水箱液位高度将影响调节阀前后的压差。该检测系统管路为闭环回路,所以主水箱液位不变。电子水泵进出口压升与水泵扬程有关,当电子水泵进出口管径一致、流量一致时,进出口介质流速相同,根据伯努利方程的推导,电子水泵扬程-压升关系式为

(3)

式(3)中,H为电子水泵在条件Q下的扬程,m;ΔZ为电子水泵进出口测压处的垂直高度差,m。

扬程与流量有关,扬程与流量设计特性由某厂家提供的某电子水泵的流量-扬程关系式为

H(Q)=-7.74×105Q2+1.99×103Q+10.32。

(4)

根据电子水泵扬程-进出口压升关系式(3)与水泵流量-扬程关系式(4)推导,该电子水泵流量-进出口压升的关系表达式为

ΔPp=ρg[H(Q)-ΔZ]。

(5)

联立(2)式与(5)式得到调节阀压差ΔPv与流量Q的关系式为

ΔPv=ρg[H(Q)-ΔZ+h]。

(6)

系统采用线性流量调节阀,即流通系数Cx与阀门开度x呈线性关系。通过实验数据获取调节阀开度、压降、流量进行线性拟合,得到阀门开度x与流通系数Cx的关系式

Cx=6.20×10-6x+4.47×10-5。

(7)

式(7)中,x为阀门开度,%。

联立(1)、(6)、(7)式,解得该电子水泵检测系统内流量点达到平衡时,阀门开度与流量的关系式为

(8)

2.1.2 调节阀传递函数

调节阀的动态响应性能与阀门结构、流体状态、负载条件等多种因素有关,其数学模型复杂。本文采用时域法辨识调节阀的传递函数。给定开度值65%的阶跃信号,对调节阀进行实验建模,得到其开度响应曲线如图4。

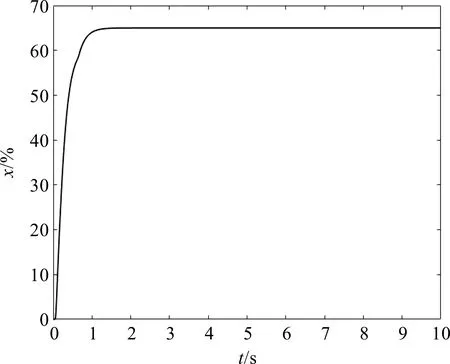
图4 调节阀开度阶跃响应曲线Figure 4 Step response curve of control valve

流量调节阀开度响应过程为一个二阶非震荡环节,且延迟时间为0,即

(9)

式(9)中,T1,T2为需辨识的系统时间参数。

G(s)相应的阶跃响应无量纲形式表达为[8]

(10)

取图4中响应曲线上的两个有明显差异的点(T1,x(T1))与(T2,x(T2)),这里取(0.2,26.75)与(0.44,52.17),代入式(9),解方程组得到T1值为0.12,T2值为0.18,则调节阀的传递函数G(s)表达为

(11)

2.2 模糊PID控制器主体设计

模糊控制器以系统的流量误差e和误差变化率ec作为输入变量[9],经过模糊化、设定模糊规则、模糊推理及解模糊等步骤,实现PID控制参数Kp、Ki、Kd的在线修改。

模糊控制器实时调整PID参数的计算公式为

(12)

式(12)中,Kp、Ki、Kd分别为经过模糊控制后PID实时变化的比例、积分、微分参数;Kp0、Ki0、Kd0分别为PID的比例、积分、微分参数的预设值,可通过试验方法调试得到最佳预设值;k1、k2、k3分别为各参数的比例因子;ΔKp、ΔKi、ΔKd为模糊推理及解模糊后的比例、积分、微分调节值。模糊PID调节的关键在于实时计算ΔKp、ΔKi、ΔKd的值。

2.2.1 输入模糊化

汽车电子水泵常见流量范围为100 L/min左右,根据系统中对流量控制的要求与测试经验,建立e和ec的基本论域为[-100 100],量化因子为0.03,则基本论域量化为模糊论域[-3 3]。确定ΔKp、ΔKi、ΔKd的模糊论域均为[-3,3]。

为保证控制的有效性,将论域定义为NB(负大)、NM(负中)、NS(负小)、Z(零)、PS(正小)、PM(正中)、PB(正大)共7种语言变量[10],则e、ec、ΔKp、ΔKi和ΔKd对应的量化等级为{-3 -2 -1 0 1 2 3}。隶属度函数可将集合映射到实数区间,考虑到稳定性与灵敏度,本文采用简单有效且应用比较广泛的三角形隶属度函数。

2.2.2 模糊控制规则

模糊PID的核心是建立合适的模糊规则表。常规PID控制根据输出响应曲线调节比例、积分、微分各参数大小,它的调节规则为若曲线的响应时间慢则增加比例参数,若稳态误差大则提高积分参数。模糊PID的调节规律基于常规PID,不同的是判断依据为误差e与误差变化率ec,根据误差与参数的规则逻辑对应关系查询模糊表得到相应的ΔKp、ΔKi、ΔKd数值。模糊规则表的建立依据[11-12]:

当|e|值较大时,取较大的ΔKp和较大的ΔKi,在减少响应时间的同时保证超调量不会过大。若ec为负数,且|ec|较大,则应取较小的ΔKp和ΔKi,以减小振荡加快系统稳定。

当|e|值较小时,取较大的ΔKp、较小的ΔKi和适当的ΔKd,加快系统响应。

当e为零时且|ec|较小时,系统即将进入稳态,取合适的ΔKp、ΔKi、ΔKd。

将ΔKp、ΔKi、ΔKd的模糊规则化为表格形式如表1。

表1 ΔKp、ΔKi和ΔKd的模糊规则Table 1 Fuzzy rules of ΔKp, ΔKi and ΔKd

基于隶属度函数可确立PID各参数的数值模糊表,通过模糊规则进行模糊推理得到各参数的输出模糊向量。对模糊向量进行加权平均解模糊即可得到ΔKp、ΔKi、ΔKd的精确输入值,计算得到Kp、Ki、Kd的实时值[13]。

3 仿真与实验

3.1 模糊PID仿真

在Matlab/Simulink中搭建水泵在线检测系统的仿真模型如图5。利用模糊工具箱设置模糊PID各参数的隶属度函数与模糊规则,实时计算误差e与误差变化率ec,并将其模糊化,在生成的模糊决策表中查询并计算相应的比例、积分、微分参数,跟踪矫正误差e与误差变化率ec,实现模糊PID控制。

图5 电子水泵在线检测系统流量模糊PID控制Simulink仿真Figure 5 Simulation of fuzzy PID flow control in test system of electronic water pump

设定实际水泵进出口高度差ΔZ=0.5 m,水箱内液面高度h=0.5 m,选取幅值为100 L/min的阶跃信号作为仿真系统输入量;经调试设置常规PID与模糊PID的初始参数值Kp0=15、Ki0=10、Kd0=10;模糊PID的各参数比例因子k1=3.5、k2=1.2、k3=0.7;设置仿真时间80 s,仿真结果如图6所示。

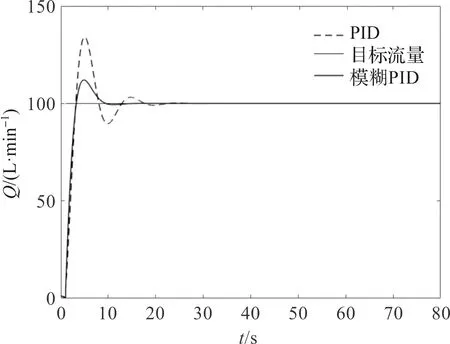
图6 PID控制与模糊PID控制仿真曲线Figure 6 Simulation curves of PID and fuzzy PID

从图6中可知,在响应曲线的上升沿时期与稳定时期,模糊PID调节速度更快:常规PID控制的稳定时间为26 s,模糊PID将这一时间缩短至14 s;超调方面,常规PID超调量为34.1 L/min,模糊PID超调量为12.1 L/min,显然使用模糊PID控制的系统调节速度更快,并且更加稳定。

3.2 实验分析

为验证模糊PID的优势,给定100 L/min的目标流量值,对第2节中的电子水泵进行测试。根据仿真生成的模糊查询表与Kp0、Ki0、Kd0初始值编写模糊PID控制程序并进行实验,基于仿真最佳比例因子值调整比例、积分、微分因子k1、k2、k3分别为3.5、2.5、0.7,设置流量采样频率为2 Hz,经过实验得到流量响应曲线如图7。

图7 PID控制与模糊PID控制实验曲线Figure 7 Experimental curves of PID control and fuzzy PID control

从图7可以看出,在响应曲线的上升沿,模糊PID与传统PID控制响应时间几乎相同,均在8 s左右到达上升沿最高点;超调方面,传统PID的最大超调量为42.8 L/min,模糊PID所达到的最大超调量为29 L/min,因此模糊PID大大降低了响应曲线的超调量;不同于仿真曲线,实际曲线受到扰动影响,两者的响应曲线在稳定期间均出现小幅度震荡,模糊PID与传统PID的稳定误差分别为±0.8%与±3.2%;若设定稳定误差为±1%,则模糊PID在100 s时到达流量测试点,完成该流量点的测试,而传统PID则需要等待至测试设定的极限时间才能够记录流量测试点。综上分析,采用模糊PID的控制方式超调量明显更小,稳定状态更优,更易快速到达流量测量点。

4 结 语

针对电子水泵性能在线检测时间长的问题,根据管路压力原理与电子水泵性能特点建立系统管路内压力关系式与电子水泵压升-流量关系式,基于实验数据进一步建立系统流量在平衡条件下调节阀阀门开度-流量数学模型。根据阀门开度-流量数学模型、调节阀的传递函数建立水泵检测系统控制仿真模型。引入模糊控制,将PID与模糊控制结合,设计基于模糊PID的电子水泵在线检测系统仿真模型,以Matlab/Simulink为平台进行仿真,并进行实验验证。仿真与实验结果均表明模糊PID在水泵检测系统的流量控制中的超调、响应速度和稳定性方面都优于常规PID。