某构件焊缝疲劳开裂的寿命预测方法应用对比

陈秉智，何正平，李向伟，兆文忠

(1.大连交通大学,大连,116028；2.中车齐齐哈尔车辆有限公司,齐齐哈尔,161000)

0 序言

某轨道车辆的一个横向减振器座，在服役过程中发现一条焊缝出现了疲劳开裂.为了寻找焊缝疲劳开裂的原因，工程中一般可采取两种方法.一个方法是取破坏部位的结构作为研究对象，在试验台上对改进的方案进行多次疲劳试验，以验证改进的方案是否满足设计寿命要求.显然这种反复试凑的过程不仅周期长，而且成本高.另一个方法是利用数值计算方法，通过模型仿真预测其疲劳寿命.很多学者都采用这种方法，并对不同的数值计算方法进行评估.例如周张义[1]对比了名义应力法和热点应力法，首次在国内详细阐述了当时在国际上引人注目的Battelle 等效结构应力法，但由于当时没有相关软件可以简便提取结构应力，而被认为不利于工程应用；柳玲[2]使用了名义应力法和热点应力法对焊接构架进行了疲劳评定，并对比了计算结果，提出了热点应力法相比名义应力法，在评价局部细节结构方面更科学的观点；Lazzarin 等人[3]采用了一种基于缺口应力强度因子的应力场方法，用于量化对称和斜对称加载模式对几何结构的疲劳影响；Rother 等人[4]讨论了IIW 建议中给出的S-N曲线的应用范围；周茜等人[5]通过简单焊缝模型，对比了包含主S-N结构应力法在内的多种疲劳寿命预测方法，并对比了其优缺点，但并没有工程实例与相关数据的验证；杨龙等人[6]对不锈钢车体点焊接头的疲劳特性做了系统的分析；邓彩艳等人[7]通过对ABUQUS 的二次开发，得到了裂纹扩展速率的变化，并预测了临界点处的裂纹萌生寿命；Wang 等人[8]建立了咬边结构的力学模型，计算了弹性应力集中系数，并预测了储罐疲劳裂纹的剩余寿命.

在工程实际问题中，准确的疲劳寿命预测模型会帮助设计人员迅速找到疲劳开裂的原因，并在此基础上对设计方案提出有针对性的修改建议.然而准确的寿命预测常常是相当复杂的.

鉴于此，针对典型的疲劳开裂案例，首先介绍了开裂焊缝仿真所需的模型及其载荷谱.采用包括名义应力法、热点应力法和结构应力法的3 种数值仿真方法对开裂焊缝模型进行了疲劳寿命预测.最后通过对比3 种方法的预测结果，给出了方法选择的建议.

1 计算对象结构及载荷谱

某轨道车辆在服役40 × 107m 后的检修过程中，发现了如图1 所示的疲劳开裂，出现在减振器座的一条焊缝上.开裂时的里程虽然不能准确确定，但应该是在40 × 107m 左右.对开裂形貌进行仔细分析，发现这是一个典型的始于上部焊趾，随后向筋板内部扩展的焊缝疲劳开裂.为了进一步确认疲劳开裂原因并给出改进方案，采用了3 种数值仿真方法对该处焊缝的疲劳寿命进行了预测.

图1 横向减振器座的焊缝开裂Fig.1 Cracking of the weld of the transverse shock absorber seat

1.1 减振器座有限元模型的创建

采用HyperMesh 软件，对减振器座及其连接结构进行建模，模型用三维块体单元离散，单元总数为287 355 个，节点总数为148 441 个.图2 为有限元模型及其载荷与位移约束的作用位置，其中F代表减振器横向力的作用方向.

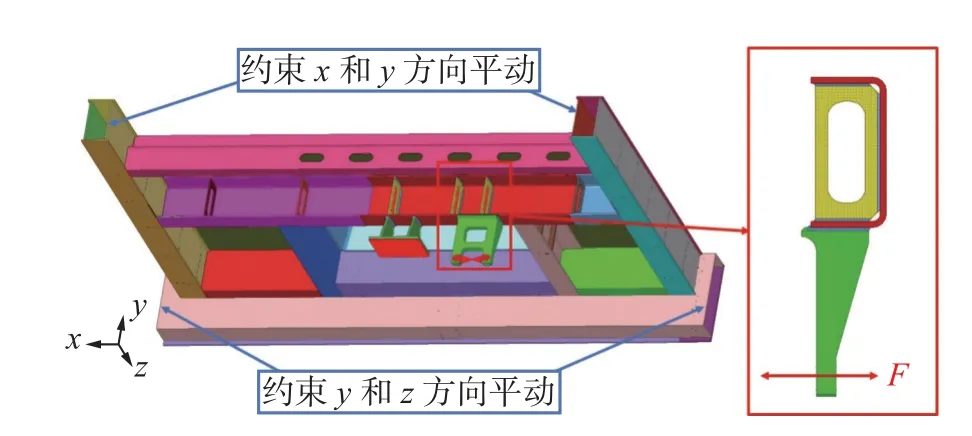
图2 减振器座数值仿真的有限元模型Fig.2 Finite element model for numerical simulation of shock absorber seat

1.2 减振器座有限元模型的创建

中国铁道科学院的科研团队选择了有代表性的线路及服役里程，在减振器的关键位置布置了若干应变片以反求服役载荷.考虑到焊接接头的SN曲线数据是以应力变化范围定义的，给出的是经过雨流计数处理后，仅包含载荷变化范围与频次的载荷谱，以用来预测该焊缝疲劳寿命.表1 给出了16 级的横向力载荷谱.

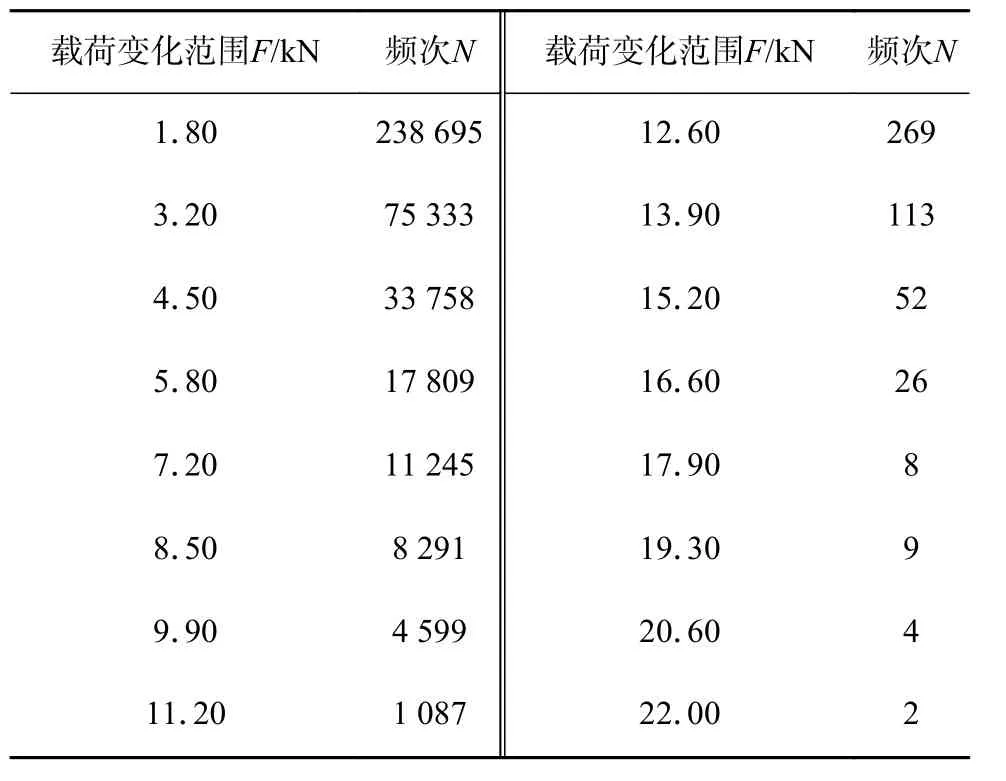
表1 减振器横向力载荷谱Table 1 Transverse force load spectrum of shock absorber

基于上述载荷谱与对应的S-N曲线数据，可计算出每一级应力变化范围的损伤比以及总损伤比，结合载荷谱历程就可以获得对应的疲劳寿命.

2 预测疲劳寿命的方法

不同的S-N曲线数据获得的方法，导致了不同的疲劳寿命预测方法.首先对3 种疲劳预测方法进行了简单概述，随后采用各方法得到了减振器座的预测疲劳寿命，并进行了比较分析.

2.1 基于名义应力法的疲劳寿命预测

名义应力法的预测基础是基于名义应力的SN曲线数据.这些数据是在实验室中，在特定的疲劳载荷下，对特定的焊接接头进行疲劳试验获得的，因此在使用S-N曲线数据时需要“对号入座”，然后基于公式(1)计算疲劳寿命，即

式中：m是双对数坐标系下S-N曲线的反向斜率；C是在S-N曲线族中区分不同曲线高低位置的常数；Δσ是焊接接头名义应力的变化范围；N是计算得到的疲劳寿命.

名义应力法在标准中得到广泛应用，例如国际焊接学会的指导文件IIW-2016[9]和英国标准BS 7608:2014+A1:2015[10]等.不管是选用BS 标准，还是IIW 标准，对图1 所示的焊接接头而言，都很难找到几何形状与载荷模式同时具有一致性的接头，如果近似选用，预测的误差必将难以估计.以IIW 标准为例，按照“对号入座”原则，只能参照接头的几何形状勉强选用疲劳等级(FAT)为71 的S-N曲线数据，其数据接头形式如表2 所示.其数据中反向斜率m=3，常数C=7.158 × 1011，可以基于公式(1)计算疲劳寿命N.

表2 IIW 标准中FAT 为71 的接头几何与载荷模式Table 2 Joint geometry and load mode with FAT 71 in IIW standard

采用名义应力法得到的疲劳预测结果为7.02 ×107m，该预测结果与实际近40 × 107m 的寿命相差很大.分析其原因，除了实际接头形式无法与SN曲线中对应的接头完全匹配外，另一个重要原因是原焊接接头的立板上并没有与表2 中完全一致的疲劳载荷.根据公式(1)可知，在线弹性范围内，疲劳寿命与疲劳载荷存在着高度非线性的下降关系，因此计算得到的疲劳寿命将低于实际寿命.

2.2 基于热点应力法的疲劳寿命预测

热点应力是名义应力的外推，其目的是获得更接近焊趾处的应力水平[11].与名义应力法类似，也是以“对号入座”的方式选一条S-N曲线数据.针对图1 所示接头的几何形状及载荷类型，只能参照接头的几何形状近似选用FAT 为100 的S-N曲线数据，其接头形式如表3 所示，其中反向斜率m=3，常数C=2.000 × 1012.文中基于热点应力法，采用了公式(2)中的递推公式得到了焊缝的热点应力.

表3 IIW 标准中FAT 为100 的接头几何与载荷模式Table 3 Joint geometry and load mode with FAT 100 in IIW standard

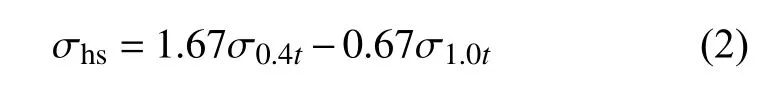
式中：t为焊缝板厚.带入式(1)中得到的疲劳预测结果为17.27 × 107m，该值与实际的近40 × 107m的寿命相差也很大.其原因与名义应力法相同，而且焊接接头所受的拉伸载荷与弯曲载荷的具体形式往往难以判断.它的疲劳寿命与疲劳载荷间也存在着高度非线性的下降关系，因此计算得到的疲劳寿命也低于实际寿命.

2.3 基于结构应力法的疲劳寿命预测

通过2.1 与2.2 节可知，基于名义应力法和热点应力法预测本案例疲劳寿命时的困难之处，主要原因是这两种方法提供的可选S-N曲线数据十分有限，因而导致“对号入座”困难.

为了克服名义应力法和热点应力法在“对号入座”方面的局限性，美籍华人科学家董平沙教授发明了一种新的方法—结构应力法，该方法于2007年正式被美国ASME 标准采纳[12].文献[13-15]已经对结构应力法给出了非常详细的介绍，下面仅对该方法的计算公式与过程予以简单归纳.

文献[13-14]给出了计算焊缝寿命的公式，即

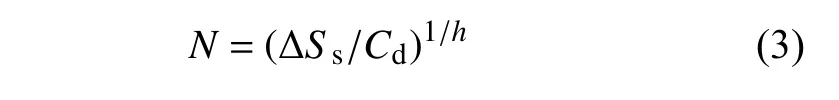
式中：Cd与h是ASME 标准中给定的试验常数；ΔSs是将焊缝上的应力集中、母材板厚以及疲劳载荷模式综合考虑的一个力学参数，即等效结构应力.等效结构应力的计算公式为

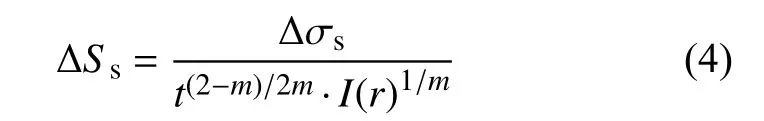
式中:m=3.6；而是弯曲比；I(r)是关于弯曲比r的无量纲系数；Δσs=Δσm+Δσb即 为结构应力，Δ σm和 Δ σb分别是膜应力和弯曲应力的变化范围.

基于结构应力法的焊接减振器座的分析过程归纳如下.

(1)在Hypermesh 软件中创建如图2 所示的有限元模型时，需要对开裂角焊缝的两条焊趾分别进行定义.图3 给出了含这两条焊趾的局部有限元模型，其中Weld1 与Weld2 分别是角焊缝两条焊趾的编号.

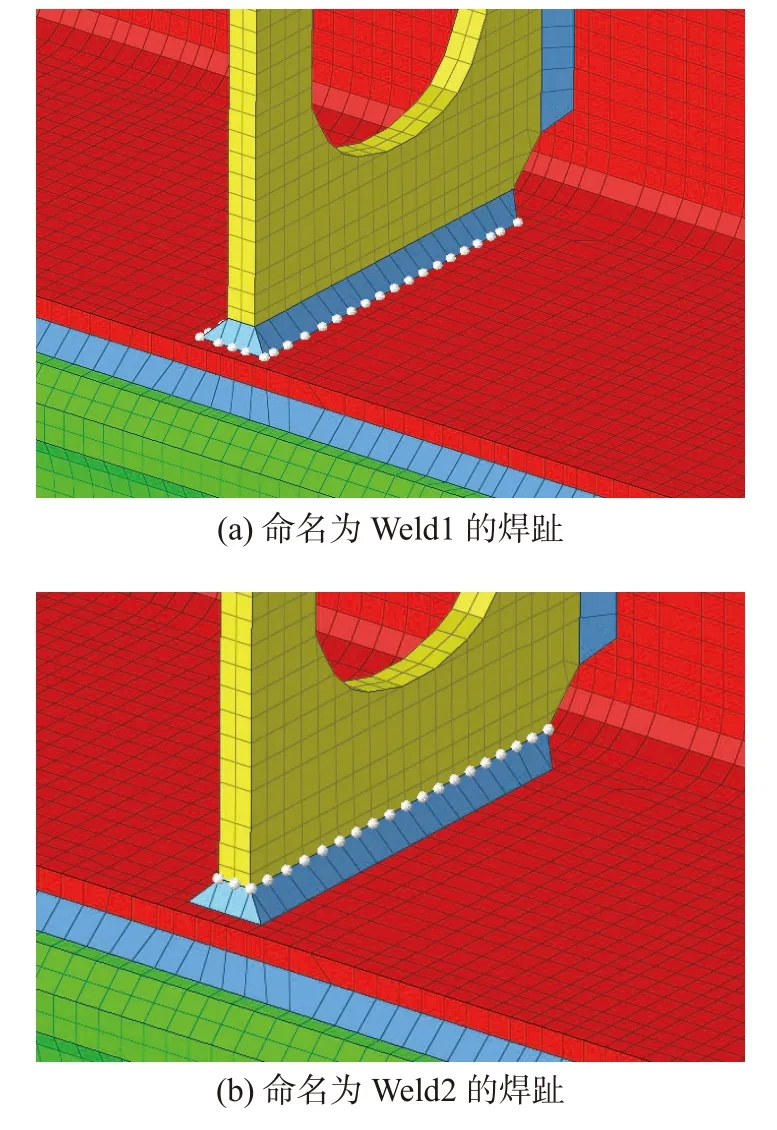
图3 定义焊缝的局部有限元模型Fig.3 Define the local finite element model of the weld.(a) weld toe named Weld1;(b) weld toe named Weld2

(2)基于表1 的分级载荷谱，利用有限元分析软件ANSYS，分别计算出这两条焊趾上与分级载荷对应的每一节点上的节点力变化范围.

(3)将节点力文件导入到已获得国家发明专利的Weld Fatigue[16]，该软件整合了结构应力法的相关公式，以下各步的计算都是在Weld Fatigue 中完成的.

(4)基于节点力的变化范围，计算各节点的结构应力变化范围，即公式(4)中的Δ σs.

(5)基于 Δσs，结合焊趾所在的板厚及载荷模式，利用公式(4)，计算出该焊趾的等效结构应力变化范围ΔSs.

(6)利用公式(3)，计算得到该焊趾每一点允许的疲劳次数N，公式中的常数来自于美国标准ASME(2007)[12].

(7)基于分级载荷谱的每级载荷的实测次数，可以计算出焊趾上每一节点在每一级疲劳载荷作用下的疲劳损伤.

(8)基于与载荷谱对应的实测里程数及Miner疲劳累积损伤原理，计算这两条焊趾上每一点的服役寿命，即在该载荷谱作用下的服役里程数.

图4 给出了筋板焊缝各焊趾点的结构应力分布，其中焊趾应力集中最大值出现在Weld2 板侧面中点处(21.213 MPa)，且该点的疲劳寿命为43.63 ×107m .由此可见，预测的开裂位置，以及近40 ×107m 左右的寿命，与实际情况基本吻合.

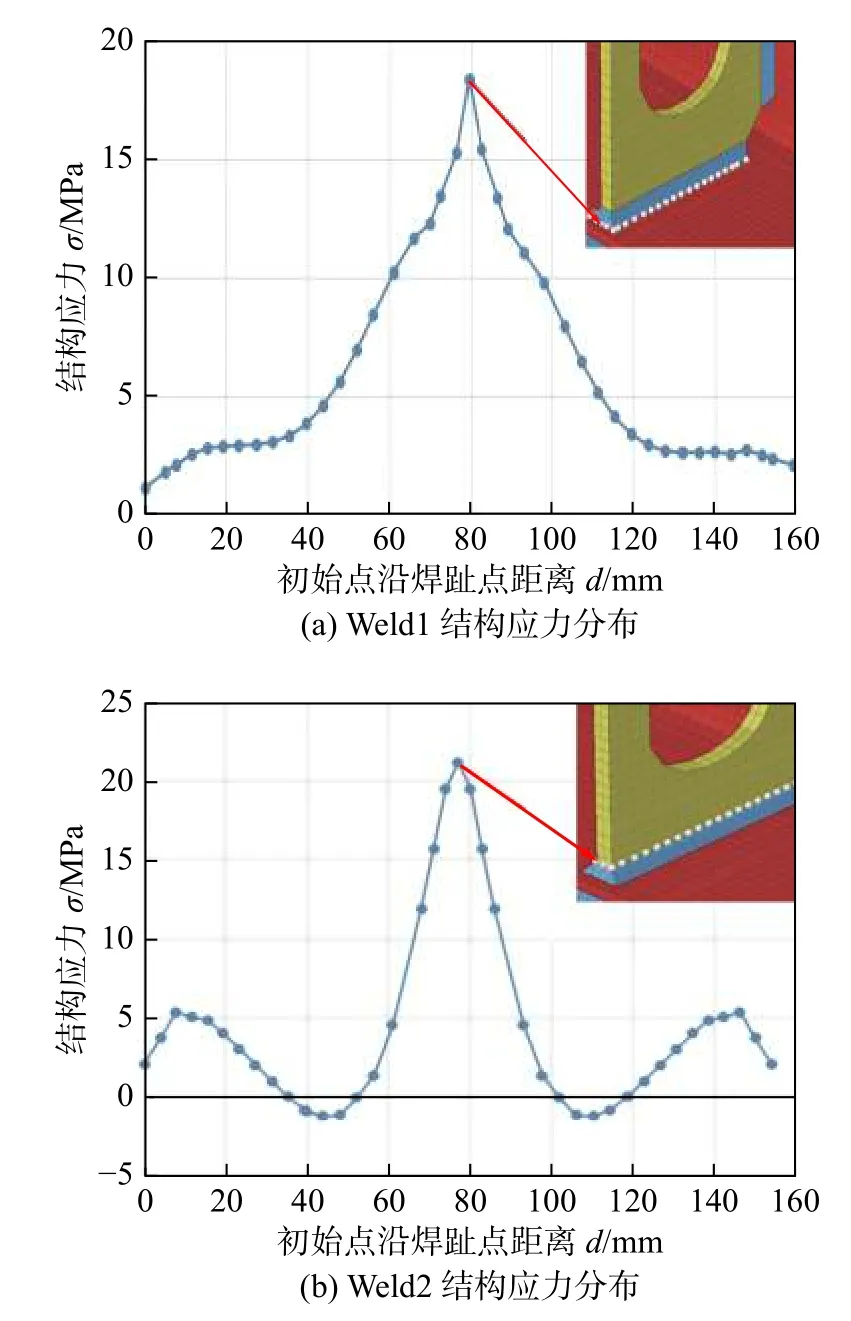
图4 各焊趾点处的结构应力分布Fig.4 Structural stress distribution at weld toe points.(a) structure stress distribution of Weld1;(b)structure stress distribution of Weld2

图4 中这种沿着焊趾的结构应力分布(应力集中分布)，对焊接结构的改进非常重要.对比之下，名义应力法和热点应力法是没有能力对焊趾上的应力集中进行上述识别，因为它们本质上不是对焊缝负责的应力计算方法.

上述3 种数值计算方法预测的疲劳寿命对比如图5 所示，基于结构应力法的疲劳寿命预测结果，优于其它两种方法的预测结果.

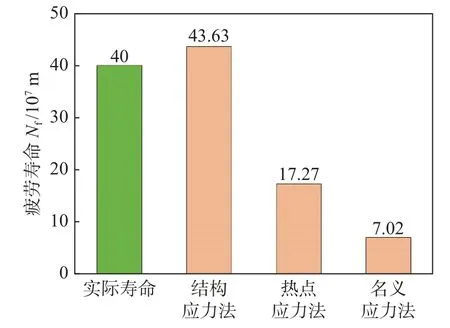
图5 3 种数值计算方法的疲劳寿命对比Fig.5 Comparison of fatigue life of three numerical calculation methods

2.4 预测方法差异性讨论

基于上述结果，可以看到结构应力法优于名义应力法与热点应力法.

(1)名义应力法和热点应力法高度依赖于实验室的S-N曲线数据，当待预测疲劳寿命的焊接接头的几何形状和疲劳载荷形式，与实验室获得S-N曲线的接头形式同时具有一致性时，名义应力法或热点应力法的疲劳寿命才是可靠的.而实验室接头类型的有限性，难以应付工程结构中焊接接头几何的多样性以及疲劳载荷的复杂性.

(2)参考文献[13-14]中提及的结构应力法，是基于理论推导且被大量疲劳试验数据证明得到的一种方法，该方法在2007 年被写入美国ASME 标准时，就曾经明确指出了结构应力法是对焊缝负责的一种评估方法：Fatigue Assessment of Welds.因此它完全可以克服名义应力法与热点应力法的上述局限性.

3 改进结构的对比验证

为了再次验证结构应力法相对于其它两种方法的工程有效性，对横向减振器座的结构进行了局部修改，并对上文预测过的同条角焊缝再次进行了疲劳寿命预测.

对原结构进行应力集中分析时，已经发现在横向载荷作用下，焊缝开裂处的应力集中是由于横向载荷作用下该焊缝处弯曲刚度不协调所致.因此基于刚度协调的设计原则，对原结构进行了如下修改：①将有孔筋板改为无孔筋板；②在槽钢开口一侧，补焊了补强薄板.局部补强结构如图6 所示.

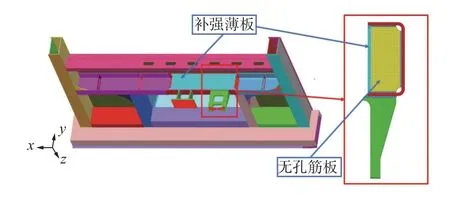
图6 减振器座补强后的局部结构Fig.6 Partial structure of the shock absorber seat after reinforcement

采用名义应力法或热点应力法，在文献[9-10]的标准中找不到与该处焊接接头匹配的S-N曲线数据，即无法“对号入座”以得到合适的计算结果，而基于结构应力法，则不存在上述“对号入座”的困难.

采用2.3 节给出的技术路线，重新建模、定义与求解，图7 给出了结构应力法的部分计算结果.其中应力集中峰值从21.213 MPa 降为11.302 MPa，这意味着该处的应力集中得到显著缓解，而线路实测的试验数据表明，补强方案满足了设计寿命要求[6].再次验证了结构应力法优于其它两种方法.

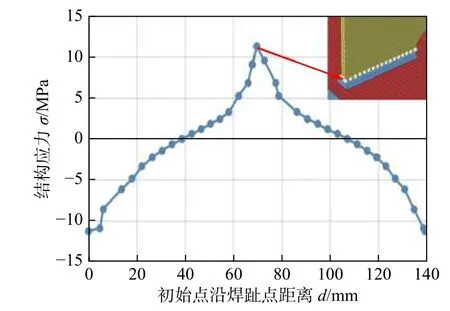
图7 减振器座补强后各焊趾点处的结构应力分布Fig.7 Structural stress distribution at welding toe points after reinforcement

4 结论

(1) 基于名义应力法或热点应力法，对焊接接头进行准确的疲劳寿命预测是困难的.因为标准中的S-N曲线数据是在特定疲劳载荷下，对特定形式的焊接接头进行疲劳试验得来的.而疲劳试验数据的有限性，使这两种方法很难覆盖接头及疲劳载荷的工程多样性.

(2) 结构应力法是一种基于理论且对焊缝负责的疲劳寿命预测方法.只要给定疲劳载荷，结构应力法都有能力可靠地预测其疲劳寿命，且不存在“对号入座”的困难，值得重视与广泛推广.

(3) 在位于焊接结构抗疲劳设计的上游阶段，如果能将结构应力法与有限元分析技术融合，则可以为焊接结构构造一个“虚拟疲劳试验平台”，而这种与位居下游的疲劳台架试验互补的技术，将带来显著的经济效益.