基于深度神经网络的教学质量评价的研究
2022-05-15陈暄

摘要:为了有效地提高教学质量,促进整体教学水平的提高,提出了使用人工智能的神经网络算法用于评价教学质量。首先,建立教学质量评价指标模型,其次,通过调查问卷收集教学评价数据确定一级指标和二级指标,最后,通过双叠加RBM-BP神经网络模型对评价数据进行分析。实验表明该评价模型能够有效提高教学评价的质量,促进教学的发展。
关键词:人工智能;教学质量;评价
引言
教学质量水平是一个学校教学工作中的重要标志,在国家“双高”政策的影响下,高职院校应该需要更加注意教学质量水平,这样才能更好的适应当前教育的新形势的要求。教学质量的评价对于提高教学质量具有举足轻重的促进作用,它能反映教师在教学过程中存在的问题,引导教师反思自己的教学方法和教学效果,教师提高自身的业务能力和教学水平;也有利于教学管理部门对教学质量进行有效的监督,更加科学化、制度化、规范化管理教学工作,最终促使教学质量的全而提高。在评价研究主体方面,徐晓娟等人对不同评价主体的视角、能力与经验等方面进行了分析,阐述了各主体在教师课堂教学评价中各自拥有的优势与不足,建议高校要针对不同的评价目的合理地选择评价主体,建立和完善运行机制,以提高教学评价工作的实效性;孟凡指出评教制度在利益相关者利益诉求的博弈演化中,评教主体主要有教师、学生和教学行政管理者,运用利益相关者的理论作为一种分析框架,解释和揭示学生评教制度还存在的问题及相关原因,他认为利益相关者参与治理模式,可以体现评教制度所具有的治理属性,也可以表达制度应该秉承的教学品性。在评价方法研究方面,杨德芹构建出基于统计学的教学评价模型;叶珍利用层次分析法建立课堂教学质量评价指标体系的递阶层次关系,同时求出权重向量和组合权重向量,在递阶层次关系和权重向量的基础上对学生评教、同行教师评教、专家评教和教师自评体系分别用模糊综合评价法建立更加综合的评价模型。张丽运用因子分析法理论模型,找出较科学、合理的评价指标体系。在评价理念方面,暴奉睿从两种评价制度的定义与内涵、关注方向、评价主体及评价结果反馈四个方面进行利弊分析。杨彩霞等人提出基于学生学习、发展和学习成果的视角的“以学生为中心”的高校教学质量保障理念,根据这一理念建构,得出以学生为中心的教学质量保障的三大特点,进而提出组织策略、目标建构策略、服务支持策略以及评价反馈策略等教学质量保障改进策略。
本文在以上研究成果的基础上,提出了使用人工智能的技术进行对评价质量模型进行优化,并通过问卷等方式收集质量评价模型的数据,实验说明了本文模型的效果。
1.基于神经网络的教学评价模型
1.1教学质量评价指标及评价结果
教学质量评价涉及到诸多因素.本课题在走访一线教师以及相关教学质量评价管理部门意见,同时查阅文献,借鉴一些院校的教学质量评价指标体系,建立了本课题的指标体系.教学质量评价指标体系分为5个一级指标及细分的18个二级指标。其中一级指标和对应的二级指标分别是教师素质(教育教学目标是否明确、教师专业知识是否扎实、教师授课和讲解水平是否扎实);教学态度(教师辅导过程中的答疑是否耐心积极、教师是否授课认真,是否具有感染力、教师授课态度是否严谨精益求精);教学内容(教师教学概念和理论是否准确、教师教学的内容饱满,注重能力,教学内容是否联系实际,注重实践,教师的专业知识是否具有深度和广度);教学方法(教师的教学方法是否善于启发和引导思考,教师的教学方式是否存在多样性,运用是否恰当,教师是否注重学生个性发展,是否因材施教,教师是否注重激发学生的创新意识);教学效果(学生的自学能力和学习兴趣是否得到提高,学生掌握基木知识、理解知识能力是否提高,学生分析解决问题能力是否提高,学生的综合素质与创新能力是否提高)。将教师教学质量评价结果作为本文的神经网络的输出,分为优秀([0.9,1])、良好([0.8,0.89])、中等([0.7,0.79])、及格([0.6,0.69])、不及格([0,0.59])五个等级各等级的输出范围.
1.2双叠加RBM-BP神经网络
受限玻尔兹曼机-BP神经网络(简称RBM-BP),它结合了RBM和BP的优点,针对复杂、高维的大量的数据。我们利用RBM强大的特征学习能力和对高维数据的无监督学习,去除冗余特征,降低数据复杂度。这样可以降低数据的训练复杂度,提高。然而,RBM-BP 网络需要大量计算并且在训练样本库方面存在缺陷。在本课题的研究中,使用双孪生 RBM-BP 网络来实现使用少量层来减少训练次数。
双叠加RBM-BP深度学习神经网络中的参数学习率,可见层数v,隐藏层数h,和参数集共同决定了双孪生 RBM-BP 神经网络的性能。因此,参数设计复杂度比传统的单一 RBM 复杂。合理优化这六个参数是本文模型有效性的关键。使用元启发式算法优化BP神经网络参数可以提高其性能。本课题使用了更强大的鲸鱼算法对双RBM-BP深度学习神经网络的参数优化算法。参数通过WOA算法对孪生RBM-BP中的v、h和共12组参数进行了优化。在WOA算法的捕食阶段中,表示鲸鱼个体位置向量,需要优化的变量包括2组参数学习率,可见层数量v,隐含层数量h以及参数集对应鲸鱼个体位置向量,因此可以表示为在螺旋阶段中,所参与计算的优化目标函数表示为双叠加RBM深度学习网络的训练误差,表达为通过目标函数得到最优的参数v1,opt, h1,opt,1,opt以及1,opt和 v2,opt, h2,opt,2,opt以及2,opt.
2.数据来源及归一化处理
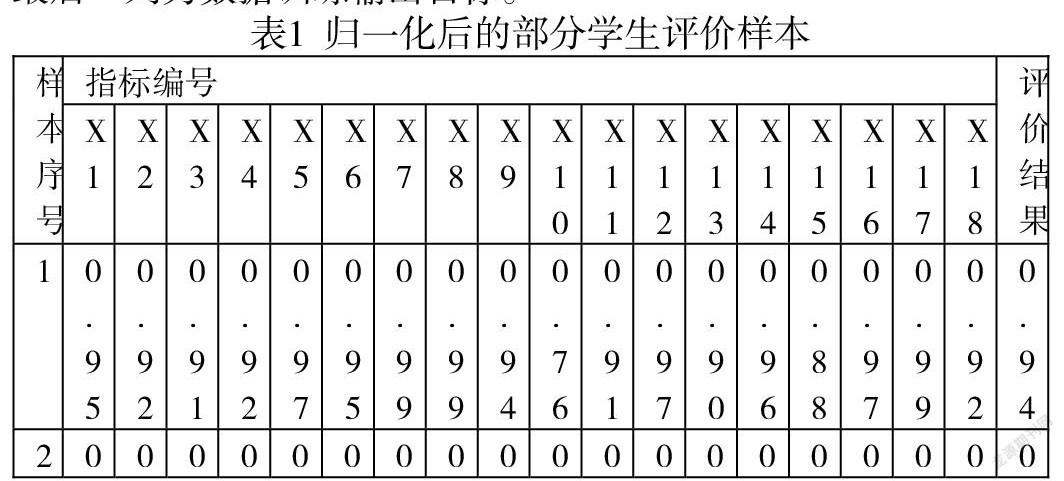
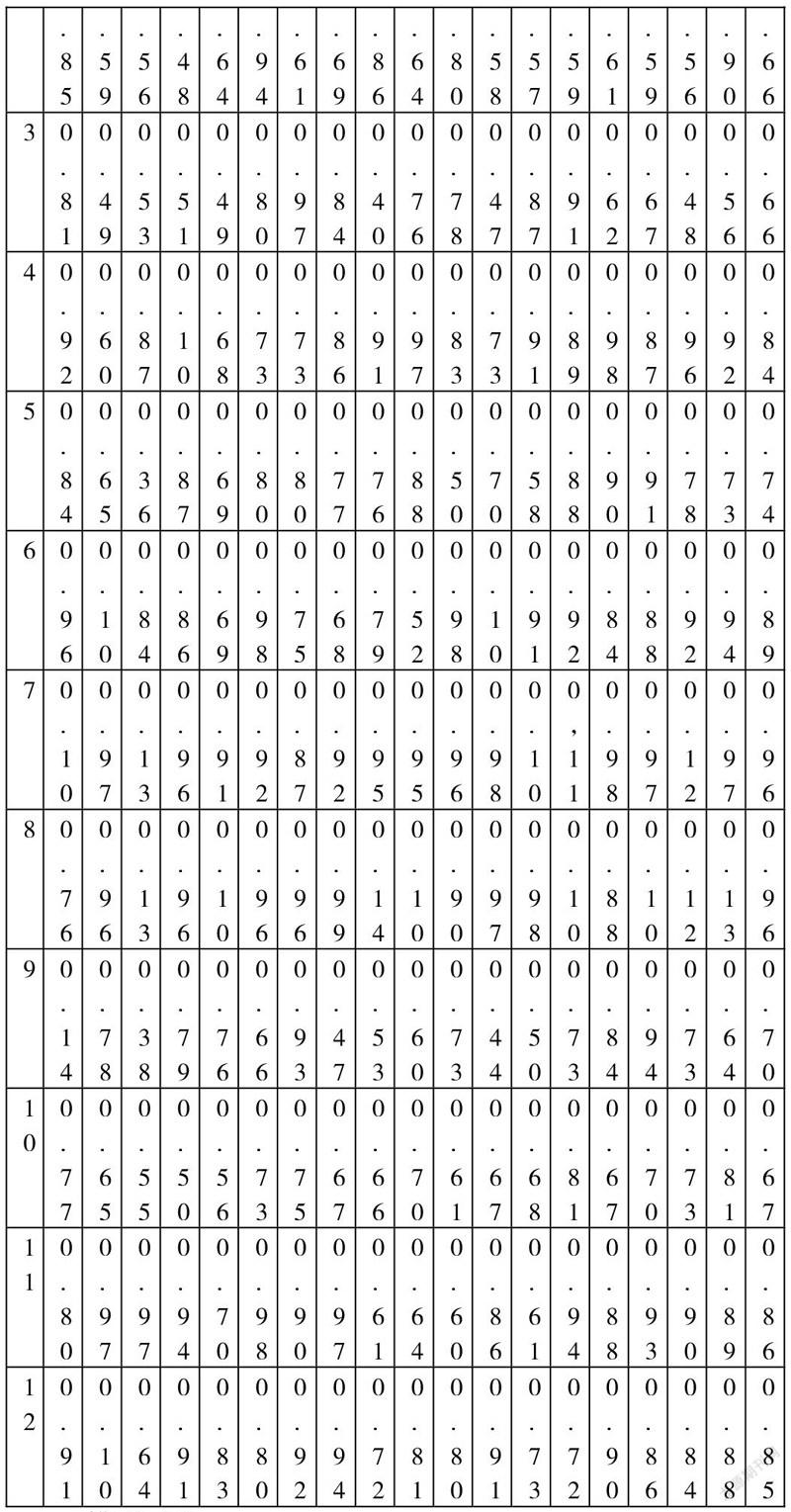
根据指标模型中的5个一级指标及细分对应的18个二级指标,使用调查问卷由学生和教师分别进行打分,对每一个指标权重值的确定由主观权重和客观权重综合获得,其中主观权重采用层次分析法,客观权重采用粗糙集的客观权重相结合。对评分数据进行收集,将在[0,100]中的评分数据的标准使用归一化中的最大最小方法对应到[0,1]之间,这样能够较好的保存原始数据。归一化后的数据作为模型的输入值。最后得到的实验数据一共有100组,其中80组用于训练模型,以便能够得到最优的RBM-BP神经网络结构,剩余的20组数据用于测试,检验神经网络处理后的学生评价的样本结果,如表1所示。每组数据的第1-18行都为输入数据,最后一列为数据训练输出目标。
3.模型对比
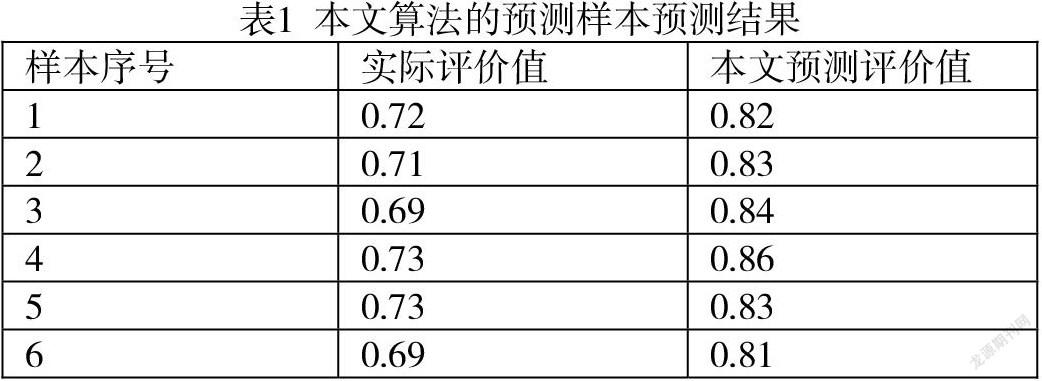
为了验证本模型的评价效果,将本文模型与BP神经网络对样本数据进行仿真。结果如表1所示。
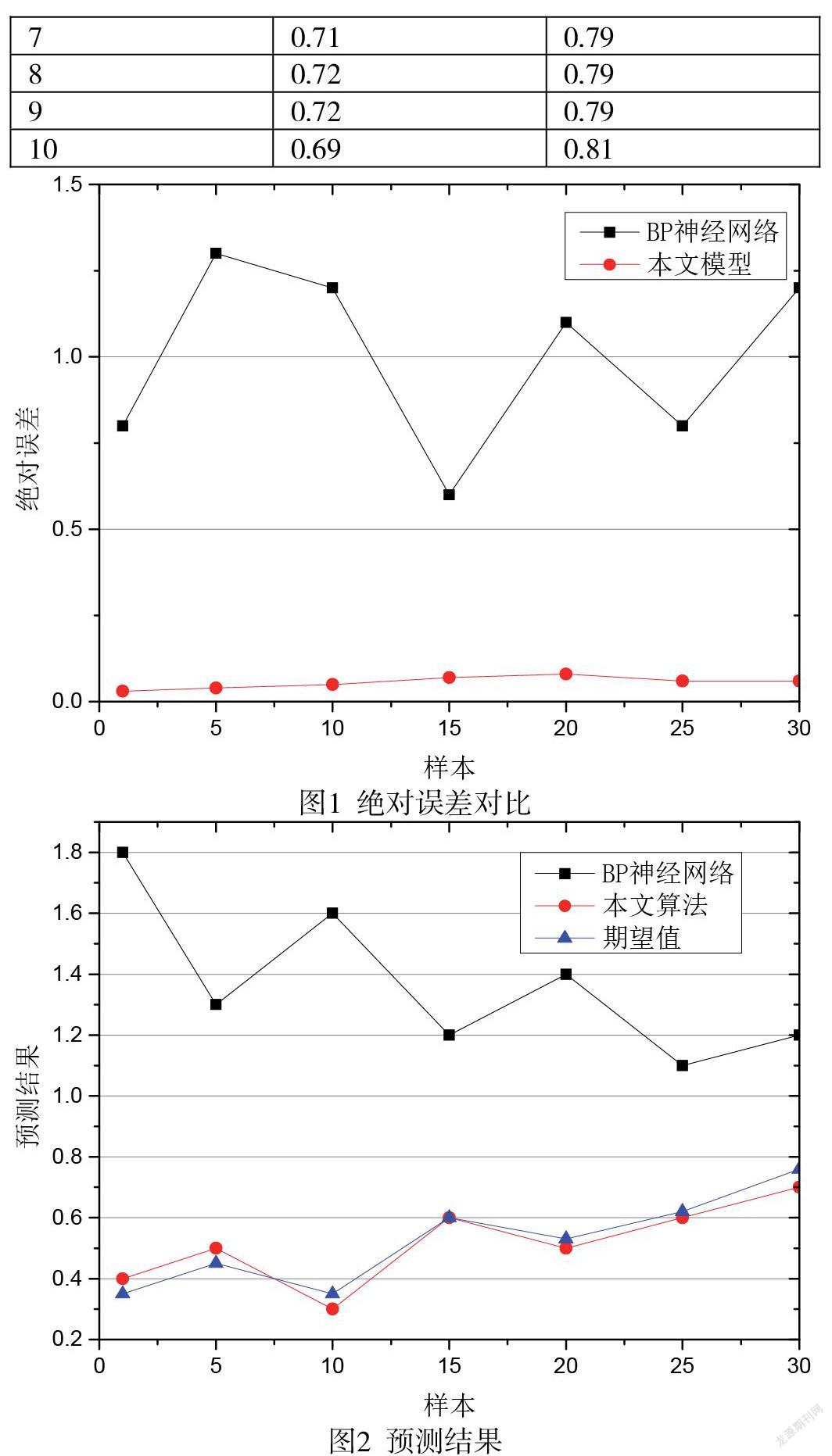
绝对误差对比图如图1所示,预测结果图如图2所示。从图中可以看出,BP神经网络的教学质量评价模型预测的绝对误差分布在0-1.48之间,10%样本预测绝对误差较大,本文提出的模型预测的绝对误差范围为0-1.05之间,90%样本评价结果预测值的绝对误差可控制在0.1以内。这说明了本文提出的模型预测结果较稳定具有更好的性能效果。
4.结束语
针对现有的教学质量评价的存在的不足,提出了将人工智能中的神经网络算法用于评价教学质量。建立了包含一级和二级指标的教学质量评价模型,通过双叠加RBM-BP神经网络模型用于评价数据分析。仿真实验,表明该评价模型能够有效发现教学质量的真實水平。
参考文献:
[1]徐晓娟,刘琦,华小洋.教师课堂教学评价主体及运行机制探讨[J].高等工程教育研究,2008(05):139-141.
[2]暴奉睿.高校教师奖惩性评价与发展性评价的比较分析[J].职业技术,2011(10):89-90.
课题来源:
浙江工业职业技术学院2021年度校级教学质量管理和监控项目—“人工智能背景下的教学质量评价模型研究”。
作者简介:
陈暄(1079.03-),男,副教授,硕士,研究方向为人工智能、教学评价。
