考虑多种类型缺陷的软件可靠性模型研究
2022-05-14闫相斌
邱 慧, 闫相斌, 彭 锐
(1.运城学院 经济管理系,山西 运城 044000; 2.北京科技大学 经济管理学院,北京 100083; 3.北京工业大学 经济管理学院,北京 100022)
0 引言
随着应用软件系统规模越做越大越复杂,其可靠性越来越难保证。应用本身对系统运行的可靠性要求越来越高,其软件系统的可靠性也直接关系到自身的声誉和生存发展竞争能力。可靠性领域学者对软件可靠性进行了研究,提出和开发了许多技术[1~3]。 为了保证软件的可靠性,软件在上市之前通常需要经过一个很长的测试阶段。在软件测试阶段,调试人员可以检测到软件缺陷并最终剔除[4]。为了研究软件在测试过程中的可靠性,许多软件可靠性增长模型被提出,其中非齐次泊松过程(NHPP)模型被广泛应用。这些模型在促进管理层做出一些重要决策(如确定最佳软件发布时间)方面发挥了重要作用。实际上,在测试阶段检测到的缺陷需要报告、诊断并最终剔除。因此,调试延迟是不可忽视的。调试延迟是指从缺陷检测到缺陷剔除的时间。在过去的十年中,学者们提出了一些考虑调试延迟的模型[5~8]。虽然这些工作使软件可靠性模型更接近现实,但是这些模型中的大多数都假设所有的缺陷都具有相同的检测率或/和剔除率。然而,这种假设在实践中可能并不正确,不同的缺陷可能需要不同的测试工作量和测试策略来将其从系统中剔除[9]。也就是说,在实际测试阶段,不同类型的缺陷可能有不同的检测或/和剔除率。检测率或剔除率在很大程度上取决于测试团队的技能、程序的大小、软件的可测试性、缺陷密度和资源分配等参数。Yamada等[10]人较早从检测过程出发,指出根据软件测试人员的测试经验可得软件一般包含两种类型缺陷:简单缺陷和困难缺陷。即,一种缺陷容易检测到而另一种缺陷难检测到。Kimura等[11,12]人再次提出根据软件测试人员的测试经验假设软件包含两种类型的缺陷,即简单缺陷和困难缺陷,并给出指数S型模型。Verma等[13]人把软件中的缺陷方便剔除的称为简单,难剔除和耗时的称为困难,比较耗时、费力和需要相当专业知识的称为复杂,结合软件升级后对原版本中存在简单、困难和复杂三种类型的缺陷进行剔除。以上研究成果为本文的开展打下了坚实的基础,但他们没有对缺陷检测过程(FDP)和缺陷剔除过程(FCP)分别进行建模。本文在已有文献的基础上,给出分类的一般模型和四种分类的具体模型。通过与一些特殊情况的比较,说明了考虑不同检测和剔除率的重要性。
1 一般模型的构建
1.1 模型假设与符号说明
假设软件缺陷总数服从泊松分布,其期望值为a。缺陷检测和剔除时间呈指数分布,将相应的指数分布的参数称为缺陷检测率和剔除率。检测缺陷具有m个类型,所占比例分别为p1,p2,…,pm(p1+p2+…+pm=1), 相应地检测率为b1,b2,…,bm。假设剔除缺陷具有n种类型,所占比例分别为q1,q2,…,qn(q1+q2+…+qn=1),相应地剔除率为c1,c2,…,cn。 假设软件缺陷的检出率和剔除率是独立的。
根据上述假设,缺陷处于第i类检测类型且第j类剔除类型的期望缺陷数是apiqj,(i=1,2,…,m;j=1,…,n)。
软件可靠性增长模型通常用均值函数表示,均值函数是在测试过程中t时刻检测过程或剔除过程中累积缺陷的期望数。因此,t时刻第i类检测类型且第j类剔除类型的缺陷在检测和剔除过程的累积缺陷数的均值函数分别为mdij(t),mcij(t)。这里下标,“d” 意为检测, “c”意为剔除,i=1,2,…,m;j=1,2,…,n。
1.2 缺陷检测过程模型建立
我们假设每种类型缺陷的检测过程(FDP)服从非齐次泊松过程(NHPP),而在(t,t+Δt)期间检测到的缺陷的期望数与在时刻t未检测到的缺陷数成正比,故有
mdij(t)=apiqj(1-e-bit)
(1)
检测过程累积缺陷数的均值函数为
(2)
1.3 缺陷剔除过程模型建立
缺陷剔除过程(FCP)可以看作是缺陷检测过程(FDP)的一个延迟过程。我们假设每种缺陷的FCP服从NHPP,并且在(t,t+Δt)期间剔除的缺陷的期望数与在时刻t未剔除的缺陷数成正比。不难得到
mc1j(t)+mc2j(t)+…+mcmj(t)
(3)
剔除过程累积缺陷数的均值函数为
(4)
2 具体模型的构建
对软件系统进行测试时,经常会遇到有些缺陷花很少的时间就能检测出来或进行剔除。反之,由于技术人员专业水平和系统难度系数等因素有些缺陷很难检测出来或者剔除成功。为了进一步说明问题,我们构建具体模型,即把缺陷分为四种类型。假设缺陷分为四类:1)容易检测和容易剔除;2)容易检测但难以剔除;3)难以检测但容易剔除;4)难以检测和难以剔除。
假设容易检测的缺陷比例为p,容易剔除的缺陷比例为q。由于容易检测的缺陷不一定容易剔除,所以假设容易检测过程和容易剔除过程是相互独立的。因此,容易检测和剔除的缺陷期望数是apq,容易检测和难以剔除的缺陷期望数是ap(1-q),难以检测和容易剔除的缺陷期望数是a(1-p)q,难以检测和难以剔除的缺陷期望数是a(1-p)(1-q)。
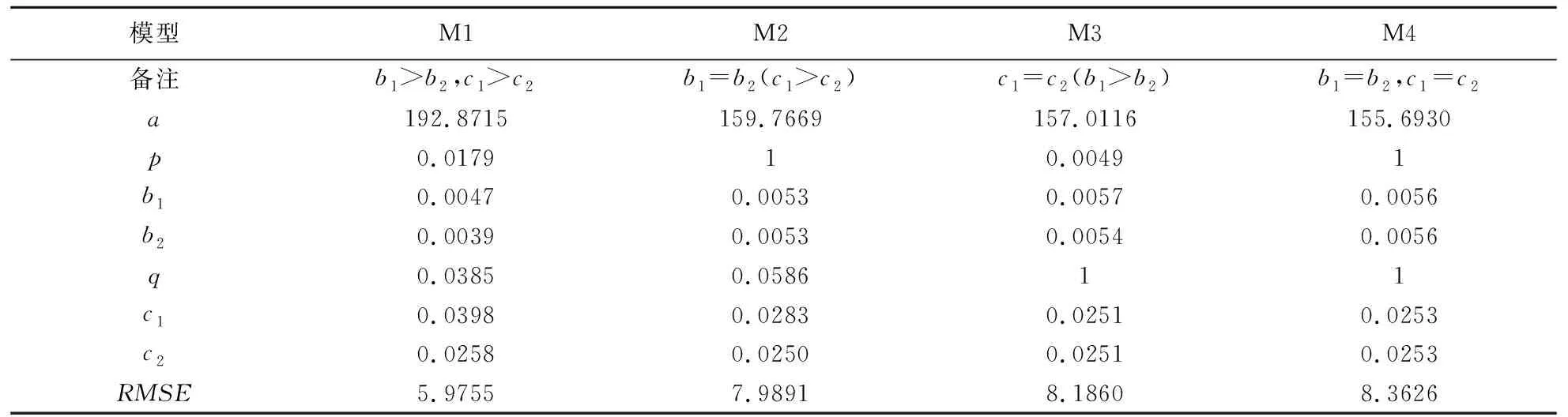
容易检测的缺陷检测率为b1,难以检测的缺陷检测率为b2,且b2 在我们的案例中,假设有四种类型的缺陷其检测过程和剔除过程的均值函数可以表示为mdi(t)和mci(t)。其中下标“d”表示“检测”,“c”表示“剔除”,“i=1,2,3,4”表示缺陷类型。 我们假设每种类型缺陷的检测过程(FDP)服从非齐次泊松过程(NHPP),而在(t,t+Δt)期间检测到的缺陷的期望数与在时刻未检测到的缺陷数成正比,故有 md1(t)=apq(1-e-b1t) (5) md2(t)=ap(1-q)(1-e-b1t) (6) md3(t)=a(1-p)q(1-e-b2t) (7) md4(t)=a(1-p)(1-q)(1-e-b2t) (8) 将这四种类型缺陷组合在一起,得到检测过程累积缺陷数的均值函数为 md(t)=ap(1-e-b1t)+a(1-p)(1-e-b2t) (9) 这里,md(0)=0,md(∞)=a。 由公式(15)可得,在t时刻的检测率为 (10) 对于这四种类型的缺陷,FCP可以看作是FDP的一个延迟过程。由于类型1缺陷和类型3缺陷都易于剔除,因此我们将它们放在一起建模。类似地,我们将缺陷类型2和缺陷类型4放在一起建模。很容易得到, (11) (12) 结合公式(11)和(12)得到剔除过程累积缺陷数的均值函数为 a(1-q)(1-e-c2t) (13) 为了说明考虑四种类型的优点,我们需要与特殊情况进行比较。为了便于讨论,将(9)和(13)所描述的模型称为M1。这里选择检测缺陷不分容易和困难,剔除缺陷有容易和困难两种情况,即缺陷检测率相同,但剔除率不同的模型记为M2;检测缺陷有容易和困难两种情况,剔除缺陷不分容易和困难,即缺陷剔除率相同但检测率不同的模型记为M3,检测和剔除缺陷都不分容易和困难的模型记为M4。 数据集来自罗马航空发展中心的System T1数据[7]。该数据集应用广泛,既包含缺陷检测数据,又包含缺陷剔除数据。表1显示了前21周内检测到的缺陷和剔除的缺陷的累积数。在此期间,消耗了300.1小时的计算机时间,发现并剔除了136个缺陷。 表1 数据集:系统T1 本算例使用最小二乘法对数据集进行了拟合。四种模型M1~M4对数据集的估计参数见表2。 表2 数据集模型参数估计值 从表2可以看出, 在模型M1中的待估参数a(缺陷总数)的值与Kapur和Younes[14]报告里面三年后测试检测到的缺陷数量188非常接近。从模型M1中可以看出,故障容易检测率b1并不等于故障难检测率b2,这表明容易检测和难检测的现象存在。类似的,故障容易剔除率c1并不等于故障难剔除率c2,这表明容易剔除和难剔除的现象存在。特别地,模型M1的RMSE值明显小于其他三种模型的值。模型M4的RMSE值是最大的,它表明,如果不区分容易和困难两种类型,结果是最坏的。结果表明,考虑不同的检测率和剔除率确实有一定的优势。 本算例使用两种预测有效性度量方法对模型进行检验。四种模型M1~M4的预测度量结果如表3所示。 在给定算例21组数据集中分别选取15组、19组数据拟合模型,然后用剩下的数据进行预测有效性分析。 从表3可以看出, 在RMSE预测方法中k=15与k=19时,模型M1的RMSE值都是最小的。在ARPE预测方法中k=15与k=19时,模型M1的ARPE值也都是最小的。由此我们最终应该选择模型M1。即,考虑不同的检测率和剔除率结果优于其他模型。 表3 预测度量结果 确定最佳发布时间是软件项目的一个关键决策,它通常考虑成本和软件可靠性。在本节中,基于所提出的模型构建考虑成本和软件可靠性的最优发布策略模型。假设在可靠性约束下使总成本最小化的最优发布时间为。据此,基于混合准则发布策略模型如下: min:C(T)=k1[md1(T)+md2(T)]+k2[md3(T)+md4(T)]+k3[mc1(T)+mc3(T)]+ k4[mc2(T)+mc4(T)]+k5[md1(∞)+md3(∞)-mc1(T)-mc3(T)]+ k6[md2(∞)+md4(∞)-mc2(T)-mc4(T)]+k7T (14) 为了验证模型的有效性,我们使用第二部分的模型M1来求解软件发布策略。模型M1的参数分别为a=192.8715,p=0.0179,b1=0.0047,b2=0.0039,q=0.0385,c1=0.0398,c2=0.0258。假设k1=50,k2=100,k3=200,k4=300,k5=1000,k6=1500,k7=30,ΔT=12,R1(T)=0.95,R2(T)=0.95。将这些参数代入成本函数和可靠性准则约束条件中,就可以得到软件最优分布时间。 图1 M1模型的成本函数和可靠性准则图 当R1(T)=0.95时,T1=807.4737。当R2(T)=0.95时,T2=1323。成本函数C(T3)最小值为110700,这时使得成本函数最小的T3=892.4593。关于约束条件(可靠性准则),R1(T),R2(T)和成本函数C(T)的图形如图1所示。在图1中我们可以看到,当考虑R1(T)和C(T)时,最优分布时间等于成本函数取得最小值时的时间,即T3。 因此,最优分布时间T*=892.4593。相应的最小成本C(T*)=110700。当考虑R2(T)和C(T)时,最优分布时间等于T2。因此,最优分布时间T*=1323,相应的最小成本C(T*)=117360。 本文提出了一种考虑多种类型缺陷和不同检测/剔除率的软件可靠性建模框架。为了进一步解释模型框架,给出四种类型缺陷的具体模型。具体分类情况可以根据模型的检验方法(拟合准则和预测有效性度量)和模型复杂度来具体决定,如果有测试人员的分类建议或者分类数据,可以结合模型共同决定。已有故障分类文献,只考虑了一种过程,本文提出了缺陷检测和剔除两种过程的模型。首先从两种过程:缺陷检测过程(FDP)和缺陷剔除过程(FCP)出发,给出考虑多种类型缺陷的一般模型,然后构建四种类型缺陷的具体模型。四种类型分为:1)容易检测和容易剔除;2)容易检测但难以剔除;3)难以检测但容易剔除;4)难以检测和难以剔除。为了验证模型的有效性,对考虑四种类型缺陷的模型与实际数据集进行了拟合和预测有效性度量。结果显示了考虑不同类型缺陷效果最好。最后,为了对模型进行实际应用,给出了软件最优发布策略。 本文假设缺陷是否容易剔除与缺陷是否容易检测无关。在未来,可以研究易检测性和易剔除性之间的依赖关系。另一项未来的工作是将缺陷引入效应也纳入其中。例如,可以假设在剔除难以剔除的缺陷时,往往会引入更多的缺陷。2.1 缺陷检测过程模型建立
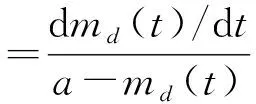
2.2 缺陷剔除过程模型建立
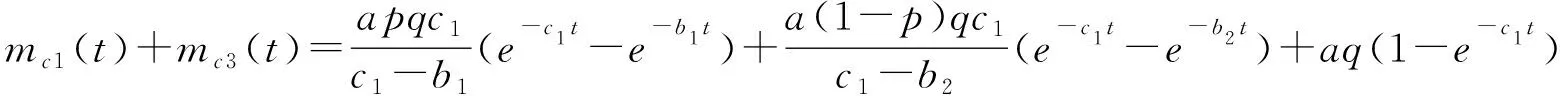
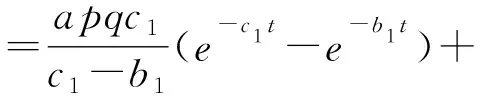
2.3 模型比较
3 算例分析
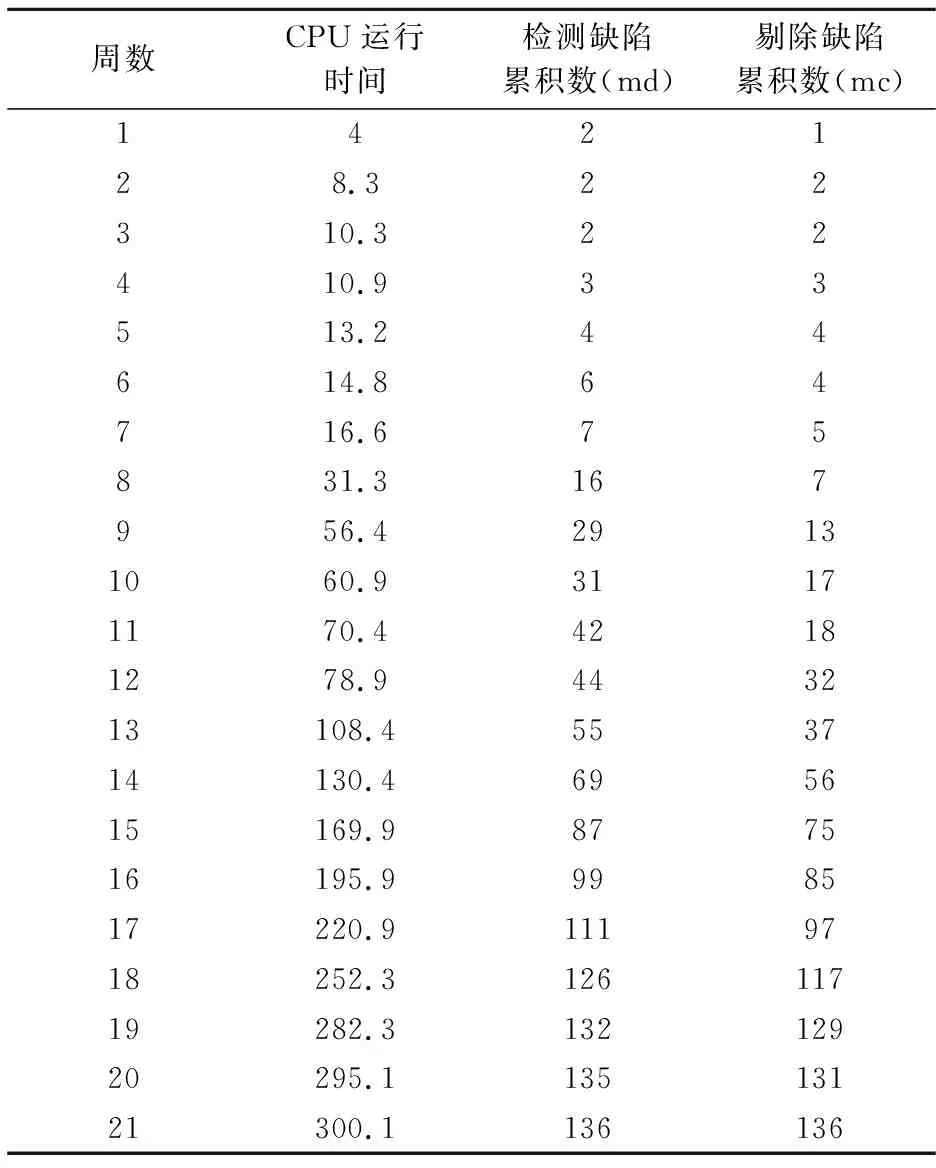
3.1 拟合效果分析
3.2 预测有效性分析

4 软件发布优化策略
4.4 软件发布策略算例分析

5 结论
