考虑投资人过度自信偏好的占线股票投资策略研究
2022-05-14丁黎黎刘梦溪康旺霖
丁黎黎, 刘梦溪,2, 康旺霖
(1.中国海洋大学 经济学院,山东 青岛 266100; 2.山东管理学院 经贸学院,山东 济南 250357; 3.山东科技大学 经济管理学院,山东 青岛 266590)
0 引言
改革开放以来,我国股票市场不断壮大与完善。截止2017年底,我国股票市场的市价总值由最初的1048 亿元增至57万亿元,股票投资人数也高达1.3亿人次。伴随着股票市场的蓬勃发展,如何更好地设计股票投资策略、增加投资者收益成为金融领域研究者所关注的热点。传统研究通常假定理性投资人可以依据股票市场中的历史数据与公开信息选择良好的投资时机,通过股票价格的变化以获得收益,即“低价买进、高价卖出”所得到的差价[1]。然而,现实中真实的股票价格并不能完全反映“所有真实可得的信息”,这也是有效市场假说理论的悖论之一[2]。因此,面对未知或知之甚少的股票价格,传统金融学理论已无法帮助投资人设计更有效的股票投资策略。
近年来,在线算法与竞争分析理论逐渐被引入金融投资决策的研究中。El-Yaniv等[3]创造性地将计算机科学与金融学相结合,提出了一类金融资产的占线交易问题(online conversion problem),即投资人在应对各种不确定性金融价格时如何设计出更好的占线投资策略,并运用竞争比方法(competitive analysis)度量占线投资策略设计的优劣。已有研究主要集中于股票、外汇等金融资产的占线交易问题。针对股票占线投资,Cover[4]首次将在线理论应用于投资组合选择,提出了多阶段“购存”的占线投资策略。张永等[5]、杨兴雨等[6]基于Cover等人的研究,结合集成有限个专家意见的弱集成算法,对占线投资组合策略进行了改进。针对外汇占线投资,El-Yaniv等[7]率先将外汇兑换问题巧妙地抽象成占线兑换模型, 设计了汇率骤然下降最坏情形下的单方向占线外汇交易策略。徐寅峰等[8]将投资人的风险偏好引入到单方向占线外汇交易策略中,改进了El-Yaniv等证明的最优竞争比,并利用博弈论中的maxmin定理,设计了价格递增情形下的最佳购存策略。
伴随着行为金融学的兴起,学者开始逐渐关注到股票投资者的金融异象行为,如股票的频繁交易。2015年,我国主板市场换手率已达到609%,创业板则高达1259%。相对于发达国家和地区,我国股票市场已出现显著的高溢价现象。从行为金融学角度而言,学界普遍认为是投资者心理认知偏差影响了股价的走势。过度自信作为投资者一种常见的心理偏好,已被证实存在于股票市场。现有关于过度自信的研究涵盖两方面:一是关于过度自信定义、表现及特征的理论研究。学者普遍认为过度自信是投资人对自身投资能力与掌握信息优势的认知偏差,主要表现为过高估计、过高定位和过度精确[9~12]。二是关于过度自信对证券市场的影响研究。多数结果表明,相对于理性投资者,具有过度自信偏好的投资者对股票价格的波动具有重要影响,即投资者过度自信会加剧股价的震荡[13,14]。
现有关于股票占线投资的研究大多遵循传统经济学的“理性人假设”,运用在线算法和竞争分析理论提供了诸多具有价值的研究结论。然而,这些研究尚未考虑股票市场中存在的异象,如过度自信、动量效应等现象的存在会导致投资者将投资收益归因于自身出众的投资能力和信息优势。因此,在进行股票占线投资策略设计时,需要进一步探讨过度自信等有限理性特征究竟会给股票投资者带来怎样的影响。
本文的研究重点是将投资人过度自信偏好、追逐股票价格动量效应等认知偏差引入到股票占线投资问题中,构建离线对手与股票占线投资人的博弈模型,分别给出一般情形和存在动量效应情形下的最优混合策略和混合策略纳什均衡。研究发现,两种情形下的最优混合策略是对传统股票投资问题研究的有益补充,一是克服了传统股票投资策略对股票价格或股票收益概率分布假设的过度依赖,解决了现实情境下投资者难以获得统计信息或信息不足的投资问题;二是将行为金融与竞争分析方法相结合,更好地抽象股票占线投资人的认知偏差特征,解决了传统竞争分析中最坏情形与现实情形过度偏离的问题,从而提高了占线股票投资策略的竞争性能。
1 问题描述与基本假设
在股票占线投资决策中,假设未来股票价格的输入序列是逐步获取的,面对每一期的实时输入,投资者必然要根据不完全信息的在线算法立即给出输出结果。在这个过程中,最关键的问题是设计一个合理的在线算法,以实现最大化收益。设Π=(I,F,U)为一个股票投资收益的最大化问题,I(I)为可能的股票价格输入集合,其中I=i1,i2,…,in;F(O)为对应的投资收益为输出集合,其中O=o1,o2,…,on;U(I,O)∈R为对应的收益函数。设ALG为股票占线投资问题的任意占线投资策略,记此占线投资策略的收益ALG(I)=U(I,O);OPT为离线策略,记离线策略的收益OPT(I)=supU(I,O),如果存在与任意输入无关的常数λ和α满足λ·ALG(I)≥OPT(I)+α,则称占线投资策略ALG为λ竞争策略,或称ALG具有竞争比λ。若α=0,称占线投资策略ALG是严格的λ-竞争比,即竞争比为λ的算法能使最优离线收益不高于投资者在线收益的λ倍。
为便于论述,本文将对下述问题进行必要的数学简化,做出如下假设:
①设股票占线投资者初期拥有m0数量的投资资金且利率为β,为简化模型,令m0=1。
②设投资者需在未来确定的n(n≥2)天内将所有初始资金投资于某一股票。在第n个交易日结束时,投资者需将其资金全部投资于某一股票,而在这期间不允许将股票卖出兑现。
③设P为所有可行的股票价格序列集合,该股票市场价格序列为p={p1,p2,…,pn}且pi+1=[pi(1-θ),pi(1+θ)],i∈Zn,θ≥0,。其中,pi为该股票在第i个交易期的价格。为了简化模型,θ为股票市场中的股价涨跌幅度。假定股票在每个交易期内只有一个价格,投资者可根据价格选择在某一交易期内是否进行投资及投资数目的多少。通常所指的交易期可以是每天、每分甚至是每秒,即任意长短期限。为了简单起见,本文将交易日作为交易期。
④假定投资者是有限理性,具有过度自信偏好。当投资者过度自信超过合理水平时,其会过度依赖于自己的私人信息进行过度交易,从而导致股价的波动增加。假设存在过度自信的占线投资者预期股价涨跌幅度由θ变为kθ,其中,过度自信水平为k且k≥1。在过度自信水平对称的情况下,k越大则说明投资者的过度自信水平越高;当k=1时,投资者则是理性的。这种以倍数关系代表过度自信水平可参见Ko和Huang[15]。
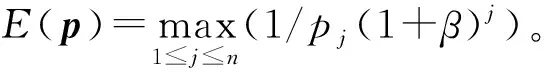
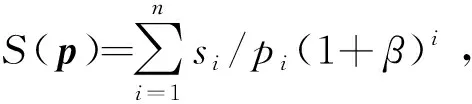
2 股票占线投资模型
本文在El-Yaniv等人的研究基础上,将股票占线投资者与怀有敌意的离线对手看作两人的零和博弈G(m,n),利用在线算法和竞争分析理论,为具有过度自信偏好特征的投资人设计占线股票投资策略。传统竞争分析通常采用竞争比分析方法,近年来也有学者提出竞争差分析法,即用差值替代比值来衡量占线算法与离线算法表现的接近程度[16,17]。与竞争差分析相比,竞争比分析所设定的目标函数的数学形式虽为复杂,但该方法在某种程度上可以提供一般意义下任何两种可供比较策略性能的统一度量[18],且能够更为直观的体现绩效改进空间。因此,本文采用竞争比分析方法进行研究,其结果对占线投资策略的改进绩效度量更具有参考意义。
当股票投资者与离线对手采取纯策略博弈时,对于任意整数x>0且Zx={1,2,…,x}时,股票占线投资问题的收益矩阵可用竞争比倒数表示如下:
(1)
这里Si表示股票投资者的纯策略,且i∈Zm;博弈中的最大化者是敌手策略,用E表示敌手的最优纯策略;pj为敌手输入的股票价格序列,且j∈Zn。
当股票投资者与离线对手采取混合策略博弈时,假定Φ(Zx)为在Zx上的概率密度函数集合,那么对x=n或m来说,每一个纯策略l都可以表示以h(l)概率被选择,这里h∈Φ(Zx)。根据Neumann的最大最小原理,有

(2)
由于收益H(i,j)为纯占线策略除以离线策略的比值。因此,股票投资者的混合占线投资策略的最优竞争比λ*为
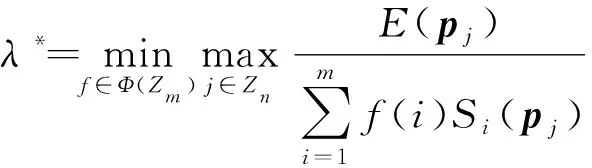
(3)
按照上述定义,股票占线投资问题实际是投资者与离线对手之间的无限次博弈,因为离线对手的纯策略是无限的,而股票投资者具有有限m个纯策略Si。
3 (n,θ,k)特征下混合占线投资策略的均衡分析
股票占线投资者与离线对手进行博弈过程中,离线对手可输入不同的股票价格序列以降低股票占线投资者的收益,因此两者进行的是无限博弈。我们利用最坏情形分析方法,将非最坏的价格序列剔除掉,把股票占线投资问题转化为一个有限策略博弈问题。因此,可以得到如下离线敌手的股票价格输入序列pj(j=1,2,…,n),即股票价格序列为每次价格浮动都达到涨跌停板的序列,没有达到涨跌幅的价格序列则被剔除。
不同于Damaschke等[19]的研究,本文考虑了存在涨跌幅约束的股票价格序列。由于我国股票市场价格涨跌幅度限制在10%以内,因此涨跌幅度满足0≤θ≤0.1。本文将投资者过度自信水平k≥1引入到占线股票投资问题中,假定投资者可以根据投资经验、外部环境等信息对涨跌幅度θ产生心理预期,形成心理预期门槛值kθ,此时存在过度自信的占线投资者的股票市场的涨跌幅度由θ变为kθ≤10%。对于占线投资者来说,离线敌手的股票价格输入序列则变为(如图1所示):
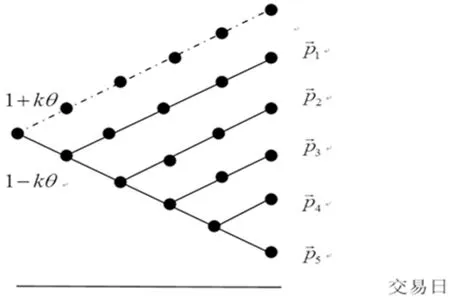
图1 离线敌手占优价格序列图
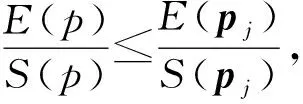
因此将价格未涨跌至涨跌幅度θ的价格剔除,将无限的离线敌手策略集合变为有限。虽然在实际生活中,股票价格上涨和下跌的顺序可能有所不同,进而导致形成的价格序列不同,但上涨和下跌的次序不会对分析结果产生任何影响。原因在于,敌手策略是尽可能的使得其收益越大越好,也就是竞争比越大越好。显然p是占优序列。
3.1 最优混合策略
将股票价格递增和递减未到达1+kθ和1-kθ的序列删除,离线对手的最优混合策略集p为如下的占优股票价格序列:价格先下跌到(1-kθ)j然后上升到(1-kθ)j(1+kθ)n-j。设Si是占线股票投资者的第i个纯策略,pj是离线敌手的第j个纯策略。对于离线敌手来说,其最优的投资策略就是在股票价格最低时买入,由于过度自信水平对称,离线敌手的最优收益E(pj)=[(1-kθ)(1+β)]-j。通过计算占线投资者的混合策略最优占线收益,可获得如下的最优混合策略及其竞争比。
定理1在(n,θ,k)已知情形下,股票占线投资问题存在混合策略纳什均衡,股票占线投资者的最优混合策略为X*(x1,x2,…,xn),即
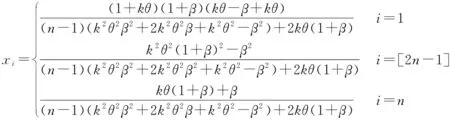
(4)
定理2股票占线投资者的最优混合策略X*(x1,x2,…,xn)的竞争比为
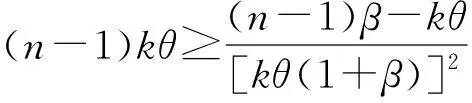
3.2 存在动量效应下的最优混合策略
3.1节中给出的最优混合策略是在假设离线敌手选择输入最坏的序列情况下得到的投资策略,这种混合策略是一种过于简单保守的投资策略。占线股票投资者从初始时就假定敌手的这种最坏的输入序列会发生,然后以一定的概率选择相对应的混合策略,因此无论敌手选择哪种价格序列的输入,占线股票投资者均能保持相同的竞争比不变。
部分学者的研究已证明现实中股票市场确实存在动量效应[20]。所谓动量效应(Momentum effect),是指股票价格在未来一段时期仍延续过去的趋势而变动。以贵州茅台为例,自2016年3月至2017年11月,贵州茅台以200元/股的股价一路攀升并突破700元/股。股票价格在近两年时间增长了2倍有余,且没有发生任何一次较大的回调。举例,假定交易期数为6天,股票价格持续上涨了5天,那么动量期为5。占线投资方基于离线对手给出的一种最坏输入序列,如
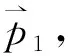
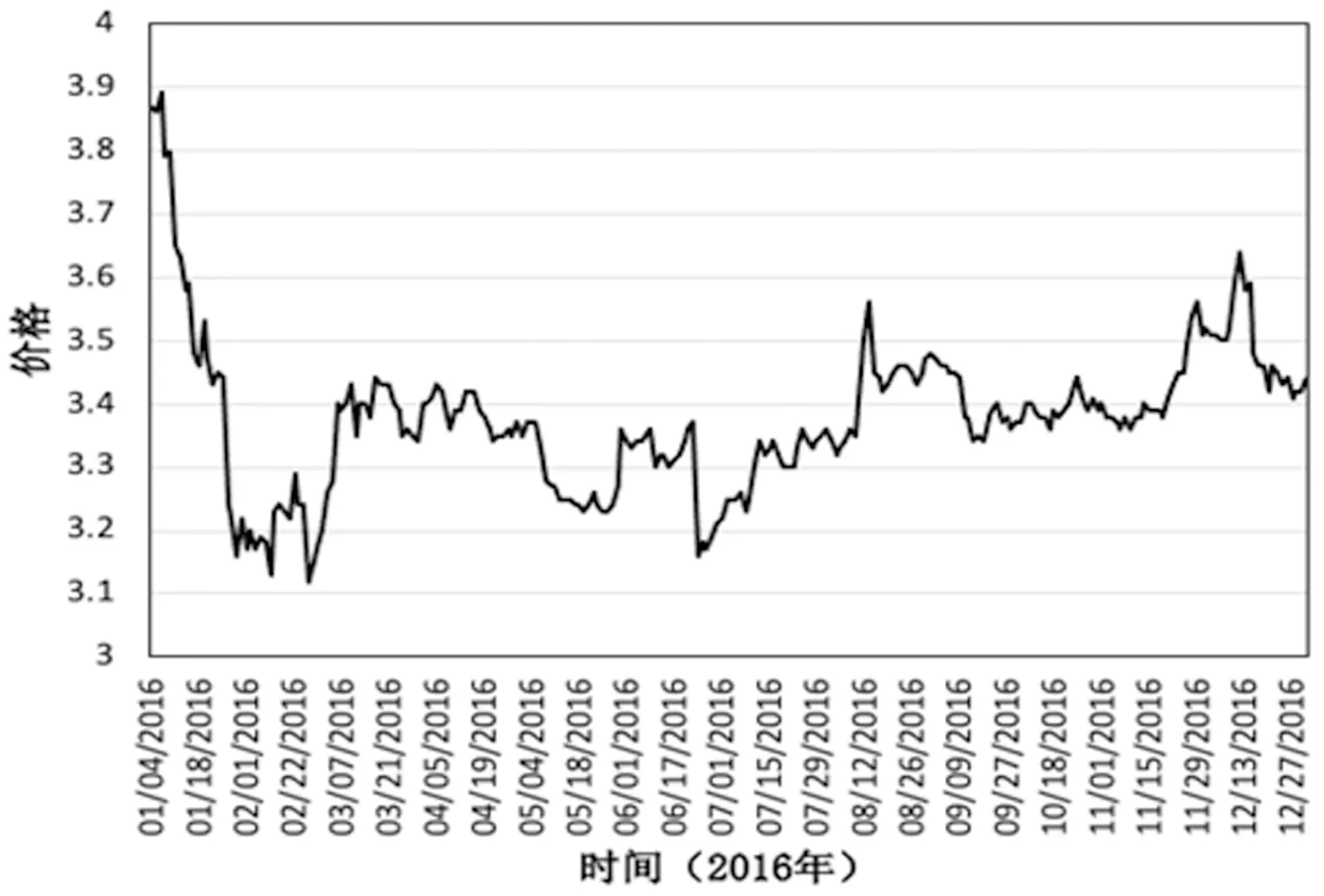
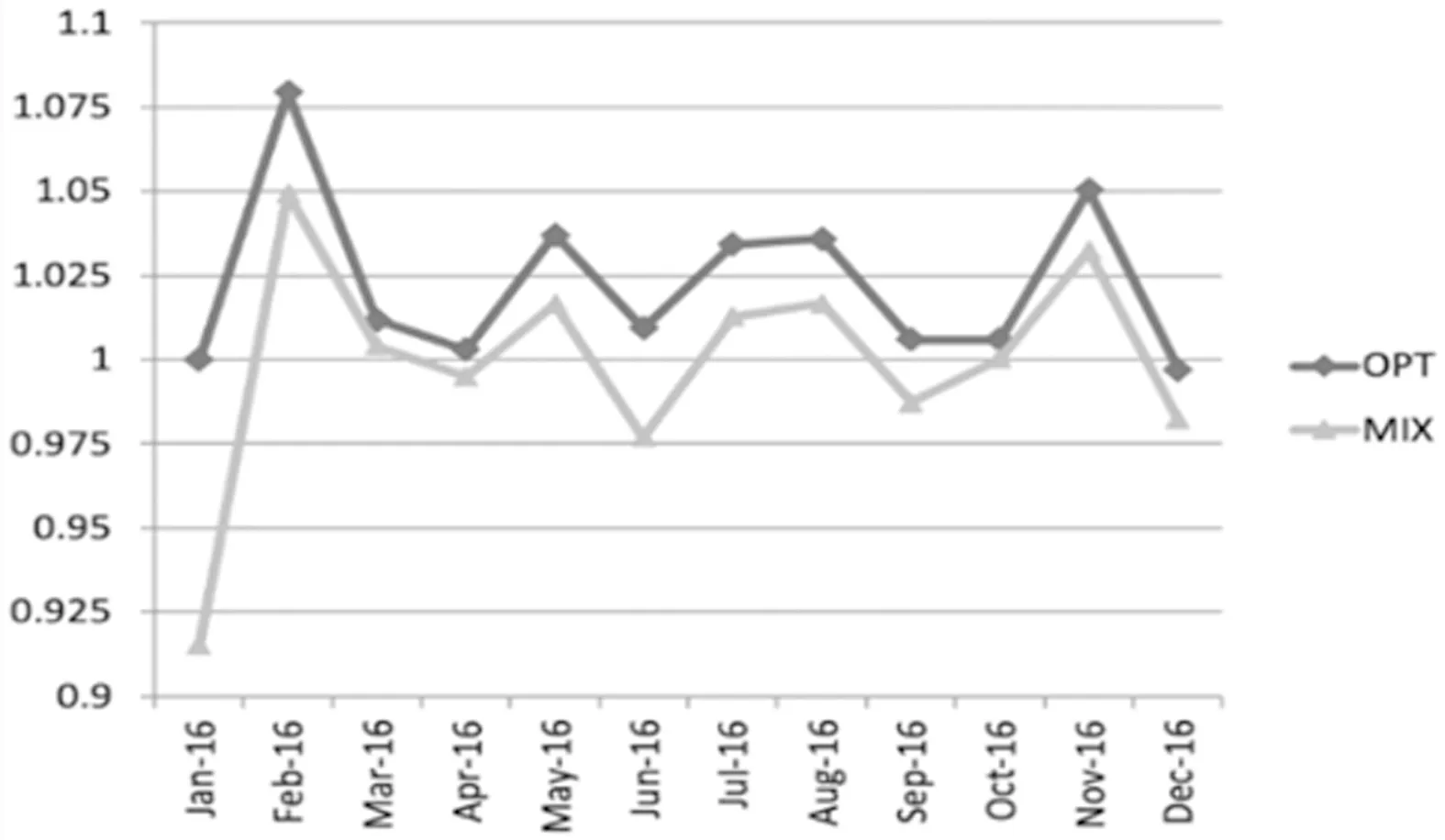
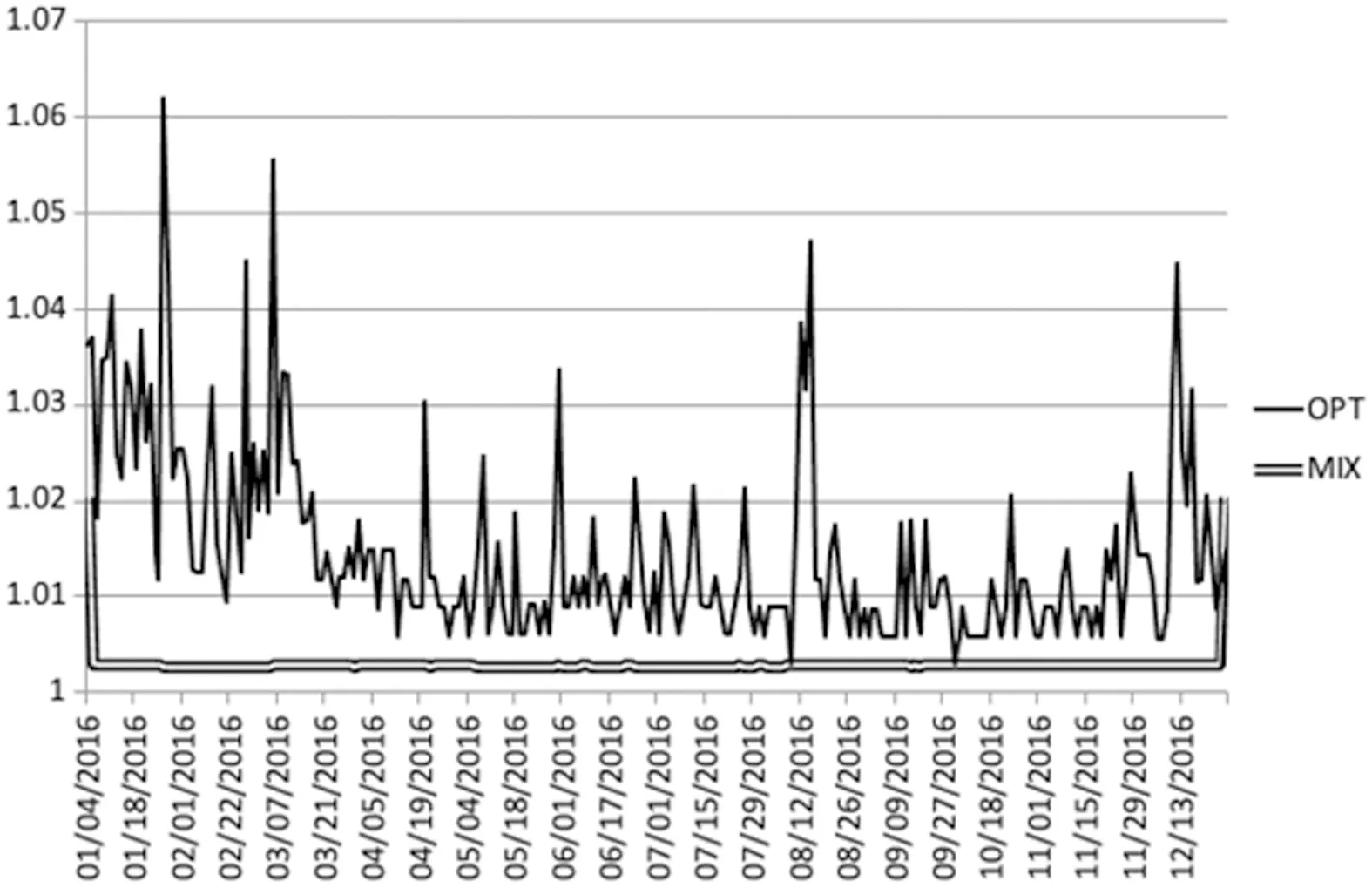
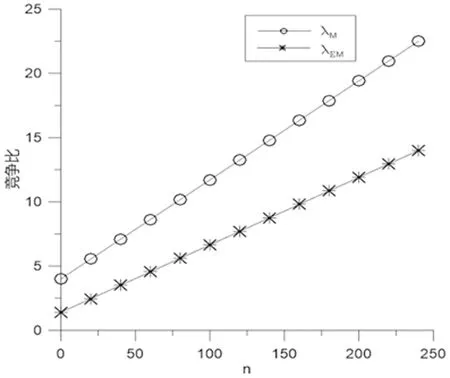
本节考虑求解存在动量效应下的最优混合策略。假定股票价格的上涨动量期为w(1≤w 推论1在(n-w+1,θ,k,mw)已知情形下,从第w天开始博弈的股票占线投资问题存在混合策略纳什均衡MNE,股票占线投资者的最优混合策略为X*(xw,xw+1,…,xn),即剩余交易期内每一期交易的数额为 (5) 结论通过分析存在动量效应下的最优混合策略可知,随着w的增大,竞争比是在减小,代表收益是递增的。联系实际的投资过程,股票市场价格未必会发生最坏的情形,此时股票占线投资者则可以结合现实中的已有信息与剩余资金的状况,根据动量效应下的最优混合策略调控投资决策过程,从而达到改善竞争比、提高收益的目的。同时也可以发现,如果市场价格真的按照最坏的情形发生,那么已有信息和剩余投资量对股票占线方来说起不到任何效果,此时股票占线投资者还可以得到与传统混合策略一样的竞争比,从而保持一定的收益。 假定股票投资者期初拥有的资金为1 CHY,股票投资者每月执行一次投资计划,以每月收盘价作为本次投资模拟过程中一个交易日的市场价格,投资者每次计划就是将手中资金的一部分买成中国银行的股票。图2所示为2016年中国银行的每日收盘价,以2016年实际一年期存款基准利率1.5%为β值。假定θ=0.05,k=0.05,n=240,为便于比较,每次投资计划的绩效由每月结束时投资者所持该股票的总份额乘以该月最后一天的收盘价,即以该股票的月末货币价值表示。 图2 中国银行每日收盘 图3所示为混合策略和离线最优策略下每月投资中国银行股票的所得收益。其中,MIX表示本文设计的最优混合策略,OPT表示离线情形下的最优收益策略。可以看出,在2、3、5、7、8、10、11月混合策略都有收益,而且所有的实际收益均小于1.10,即混合策略所得收益与最优的离线收益相差并不是太大。但是,在交易周期为一个月的情况下,混合策略收益不明显。其主要原因在于实际的市场价格序列并不是按照一种最坏的情况给出的,而是无限多个输入序列中的一种。从理论上来讲,混合策略在较短的交易期内收益并不是非常明显,在市场不景气时,甚至可能造成小幅度的亏损。 图3 MIX和OPT的实际收益比较 图4为MIX和OPT的每日累计收益比较。若将交易期延长为一年,同样分析2016年中国银行的股票,投资者采用混合策略的每日累积收益以及离线最优策略的每日累积收益如图4所示,累积收益按照投资者每天所持证券的货币价值与剩余现金之和进行计算。 图4 MIX和OPT的每日累计收益比较 在交易期结束时,最优的离线收益为1.062,混合策略所得收益为1.02。随着交易期的增长,混合策略的收益明显比离线收益趋于平稳。简而言之,在未来信息未知情形下通过竞争比分析,投资者得到的收益可以控制在一定比例之内,这种策略保障了决策效率维持在较高水平,避免在最坏情形下出现较大的损失。 在图5中,本文比较了传统混合策略M和动量效应下混合策略EM的竞争比结果。通过比较可以发现,动量效应下混合策略EM的竞争比优于传统混合策略M的竞争比。而且,随着交易期n的增加,动量效应下混合策略的竞争比相较于传统混合策略M的优势扩大。 图5 MIX与E-MIX竞争比比较 现阶段我国证券市场正处于发展的关键时期,股票市场以其自身特质为我国的经济增长做出重大贡献。股票投资一直是学术界所关注的焦点。本文基于已有学者的研究,将现实生活中投资者的过度自信心理偏好与理论模型相结合,构建了离线对手与股票占线投资人的博弈模型,分别给出一般情形和存在动量效应情形下的最优混合策略和混合策略纳什均衡,并进一步对两种情形下的结果进行对比分析。结果表明,动量效应下混合策略的竞争比整体优于传统混合策略的竞争比,此外,随着交易期的增加,动量效应下混合策略的优势逐步扩大。两种情形下的最优混合策略不仅克服了传统股票投资策略对股票价格或股票收益概率分布假设的过度依赖,而且能够更好地抽象股票占线投资人的过度自信、追涨杀跌等特征,解决了传统竞争分析中最坏情形与现实情形过度偏离的问题,提高了占线股票投资策略的竞争性能,对金融占线交易问题的相关研究提供有益补充。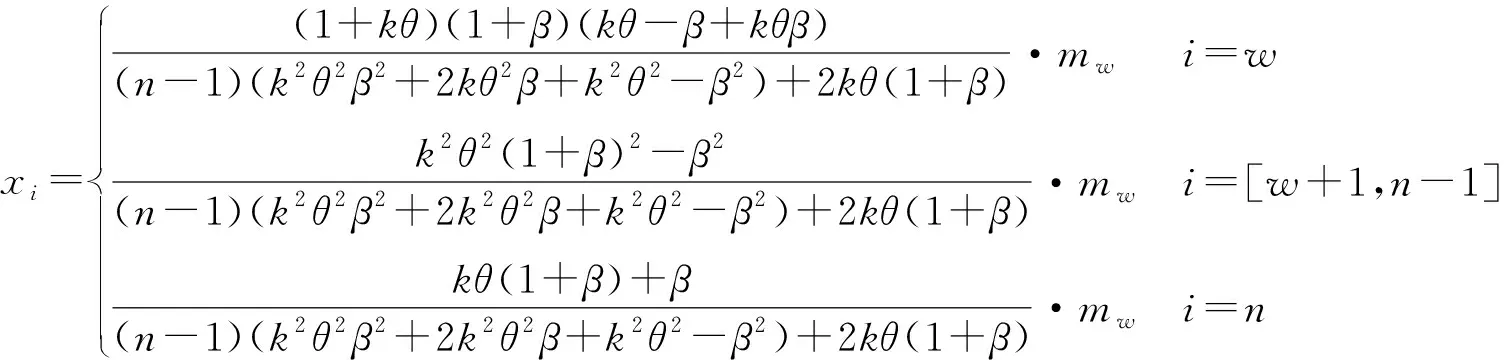
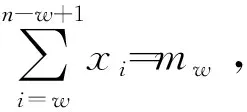
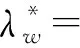
4 算例
5 结语
