考虑退货的电商平台销售策略

王雨亭, 陈克红, 王兰婷, 董 克

(1.中国科学技术大学 管理学院,安徽 合肥 230026; 2.中国科学技术大学 管理学院国际金融研究院,安徽 合肥 230001; 3.浙江教育出版社集团有限公司,浙江 杭州 310013; 4.安徽广播电视大学 经管学院,安徽 合肥 230022)

0 引言

随着电子商务和物流业的快速发展，网购逐渐成为消费者主流的购物方式。目前电商平台大致有两种销售模式：一种是转售模式，平台从制造商处购买产品，决定售价并通过自身的平台将产品直接销售给消费者，如平台的自营店；另一种是代理模式，在这种模式下，制造商通过电商平台销售产品，产品价格也由制造商决定，平台起到中介作用并收取一定的费用，如各种官方旗舰店[1]。消费者在京东商城、淘宝、亚马逊、苏宁易购等网站上购物时，既可以选择从制造商的官方旗舰店中购买，也可以在平台的自营店中进行购买[2]。

与实体店相比，消费者通过网络渠道进行购物时无法接触到产品实物，由于产品本身存在缺陷，信息的不对称性，对产品的预期和实际存在偏差等原因，往往会导致退货行为。在这些退货中，不是由于产品质量存在问题导致的退货被称为“无缺陷退货”[3]。在网络购物中，退货率对于电商平台和店铺来说都有很大的影响。2014年工商总局颁布了《网络交易管理办法》，规定除特殊产品外，消费者从电商处购物可享受七天无理由退换货，这增加了商家运营的成本，也提升了网络购物的退货率。有研究数据表明，在传统的零售业中，退货率为8.7%，而在网络零售业中，退货率高达18%～35%，其中有95%的退货是无缺陷退货[4]，也就是说产品没有质量问题，只是因为与顾客需求不匹配才导致退货。因而退货也成为商家经营中必须重视的一个问题。

不同的销售模式下，电商平台对于不同类型的退货也有着不同的处理方式。以京东商城为例，若产品有质量缺陷，无论是转售模式还是代理模式，当消费者退货时产品都将被退回到制造商处，此时对于转售模式来说，虽然平台已经购买了制造商的产品并且自己销售，但它仍可以退回存在质量问题的产品，并从制造商处得到产品的退款；当面临无缺陷退货时，在代理模式下，由于是制造商通过平台销售产品，产品依然会被退回给制造商，可在转售模式下，因为产品不存在质量问题，平台收到退回的产品时只能自己处理，承担相应损失，无法再将产品再退到制造商处[5]。因而对于电商平台而言，在如今网络购物退货率较高且无缺陷退货占比较大的情形下，退货对其销售模式的选择具有较大影响。

基于此，本文研究在考虑无缺陷退货的情况下，退货对于电商平台的影响是什么？电商平台在什么条件下选择转售模式或代理模式？电商平台的选择对于制造商又有怎样的影响？

1 文献综述

本文研究存在退货时，电商平台的模式选择问题，因此主要涉及电商平台与退货两个方向的研究。

第一个方向是电商平台相关研究，主要集中在电商平台的销售模式选择以及电商平台与制造商的渠道竞争等。国内外学者对于电商平台已有了很多研究。例如，Wei等[6]研究当制造商可以通过代理模式或转售模式在电商平台上销售产品时，两个互相竞争的制造商应该如何选择最佳的销售模式，当选定了销售模式，制造商之间的博弈关系如何影响供应链成员的利润和定价决策，以及电商平台作为供应链的领导者，又该如何引导制造商选择最优的销售模式。Abhishek等[1]使用了程式化的理论模型来回答网络零售商面临的一个关键问题：什么时候他们应该选择代理销售模式而不是使用更传统的转售模式？研究发现代理销售比转售更加有效，并导致较低的零售价格。当电子渠道的销售对传统渠道的需求产生负面影响时，电商更倾向于代理销售，反之电商更倾向于转售模式。Hagiu和Wright[7]考虑了信息在模式选择中的作用。发现当营销活动在产品之间产生溢出效应时，电商平台会倾向于选择转售模式。Shen等[8]研究了制造商如何与电商平台和传统经销商进行合作，通过协商加盟费和收入分成，制定了制造商与电商平台之间的两种议价模式。Zhang和Zhang[9]探究了电子零售商和供应商信息共享对于模式选择的影响。发现当供应商的进入成本很小或很大时，电子零售商在代理销售下共享信息，而在转售下保持信息私密性。王文宾等[10]建立了由供应商和平台商构成的基于平台的混合销售模型，分别研究了在集中式和分散式决策模型下，批发价、零售价和利润的变化，从而得到使博弈双方都能获益的收益分成比例范围。然而，这些研究都没有考虑消费者退货行为对电商平台销售模式选择的影响，本文是首先考察该影响的研究之一。

第二个方向是退货相关研究，大多集中在企业是否应该提供退货，以及不同退货政策对于企业有着怎样的影响等方面。Huang和Feng[11]研究了在不同退货政策下全国性品牌和自有品牌的博弈论模型。发现退货策略的存在对零售商有利，但对制造商不利，并且会加剧两种品牌之间的竞争，给制造商带来利润损失。Chen和Chen[12]研究在双寡头模式下，退货策略和个性化定价对于消费者的影响。并且主要考虑无缺陷退货而非质量缺陷导致的退货。黄甫等[13]运用两阶段方法，考虑退货策略对供应链产品质量和服务的影响。黄宗盛等[14]研究了双渠道销售商在什么情况下应该选择提供退款保证的问题。发现销售商的退款保证策略与两个渠道间的成本差异有关系，当差异较高时，仅在网络渠道提供退款保证是最优选择。张学龙等[15]考虑定价差异和退货风险双重因素，指出二者对供应链成员收益的影响与定价模式相关。本文主要考虑无缺陷退货对于电商平台不同销售模式的影响，与现有的退货相关研究存在较大区别。

综上所述，虽然目前已有较多关于电商平台和退货的研究，但将退货和电商平台的两种销售模式结合起来，具体考虑无缺陷退货对于转售和代理模式的不同影响是一个新的尝试。鉴于此，本研究具有创新性和一定的现实意义。

2 问题描述与基本假设

本文考虑由一个制造商、一个大型电商平台组成的供应链模型，制造商制造产品，所有产品都通过电商平台销售给消费者，但是存在两种不同的销售模式，即转售模式和代理模式。

在转售模式下，制造商以批发价w将产品出售给电商平台，随后平台以价格pr向消费者销售。当消费者退货时，产品会以退货价fr退回到电商平台，由电商平台进行处理。

在代理模式下，制造商通过平台将产品以价格pm直接销售给消费者，平台起中介作用，同时收取一定的收益分成比例θ(0<θ<1)，即向制造商收取提供中介服务的费用。当消费者退货时，产品会以退货价fm直接退回到制造商，由制造商进行处理。

我们分别用下标r,m表示转售模式和代理模式。

文中主要假设如下：

(1)电商平台处于领导地位，由它先决定提供何种销售模式。

(2)只考虑无缺陷退货。

(3)产品的生产成本标准化为0。

当产品出现质量问题时，无论使用哪种销售渠道，退货流程是相同的，即产品都会退回到制造商处。而当产品本身没有缺陷时，在转售模式下，产品只能退回到平台商处。因此这里只考虑无缺陷退货对平台销售模式选择的影响。

下面将介绍需求函数和退货函数，分别讨论制造商和电商平台在转售和代理两种销售模式下的最优定价和最优利润，然后再研究电商平台的最优销售模式决策。

3 模型分析

根据Li[16]等，产品的退货价可能会对市场需求产生正向影响，而产品价格则会抑制产品需求，因此，产品的市场需求是关于产品价格和产品退货价的函数。不失一般性，假设市场需求Di与产品价格和退货价存在线性关系，即：Di=α-βpi+γfi,其中α>0代表市场的潜在需求量，与价格和退货价无关，受非价格因素影响，例如，品牌、广告等。β>0代表价格敏感度参数，表示需求对销售价格的敏感程度。γ>0代表退货价敏感度参数，表示需求对退货价格的敏感程度。pi表示销售价格，fi表示退货价格。一般情况下，需求对销售价格比对退货价更敏感，因此假设β>γ。i∈{r,m} 表示销售模式。

当消费者收到产品后，根据对产品特性的满意程度(所购买产品与产品描述、交货速度等之间的一致性)和退货价格来决定是否退货。因此，我们用下述线性函数来概括消费者的退货行为:Ri=φ+φfi,其中Ri表示消费者的退货量，φ>0表示基础退货量，它不受价格因素影响，只与消费者对产品特性的满意程度有关，φ>0表示退货量对退货价格的敏感程度：退货价格越高，退货量越高。

3.1 转售模式

在转售模式下，制造商的利润函数为:πr=wDr。

当消费者退货时，产品会被退回到平台商处，由平台商进行处理，所以其利润函数为:Πr=(pr-w)Dr-frRr。

在这种情形下的博弈顺序为：平台作为领导者首先决策边际利润Δ和退货价fr，则有pr=Δ+wr。制造商制定产品的批发价格w。通过逆向推导法求解可得命题1。

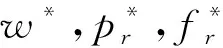
由推论1可知，在转售模式下，当产品价格对需求的影响度较高时，消费者对产品价格很敏感，价格提高会导致产品需求的大幅下降，为了留住消费者，平台会采用低价策略来提高收益，制造商也只能降低批发价，此时消费者对于退货价敏感度低，加上产品售价并不高，平台会降低退货价来获得更高利润；当退货价格对需求的影响度较高时，平台只需提供宽松的退货政策就可以吸引更多消费者购买，平台会制定较高的退货价，此时消费者对产品价格的敏感度较低，制造商和平台都可以采用高价策略；当退货价格对退货数量的影响度较高时，为了减少消费者的退货行为，平台会制定较低的退货价，此时为了提高产品需求，平台会采用低价策略来吸引消费者购买，进而提高收益，制造商也会制定较低批发价。

3.2 代理模式

代理模式下，当制造商成功销售产品时，制造商向平台支付θ的收益分成，当产品与消费者需求不匹配而被退货时，由制造商处理退回产品，并且无需为这部分产品向平台支付分成，可得制造商的利润函数为:

πm=(1-θ)pm(Dm-Rm)+(pm-fm)Rm

电商平台在这种模式下起中介作用，它的获利就是从制造商处得到的收益分成，所以利润函数为：Πm=θpm(Dm-Rm)。

在代理模式下的博弈顺序为：电商平台先决策收益分成比例θ，再由制造商决定自己的销售价格pm和退货价fm。通过逆向求导法求解得到命题2。

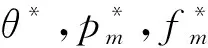
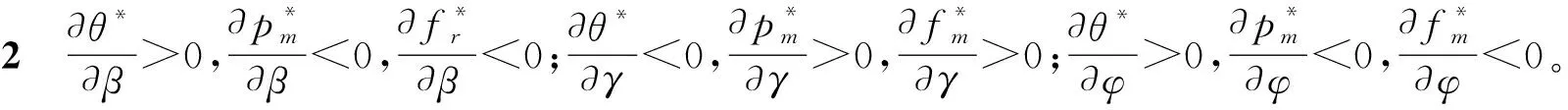
由推论2可知，在代理模式下，当消费者对产品价格很敏感时，若产品售价较高，会有大量消费者放弃购买，因此制造商会采用低价策略来吸引消费者，同时制定较低的退货价来减少利润损失，此时对于平台来说，会提高收益分成比例来获取更高利润；当退货价格对需求的影响度较高时，制造商会制定较高的退货价来吸引更多消费者购买，这时消费者对产品价格敏感度不高，制造商可以通过提高产品售价挽回损失，平台收取较低的收益分成比例也能获得较高收益；当退货价格对退货数量的影响程度较高时，制造商会制定较低的退货价来减少消费者的退货，同时用低价策略吸引消费者购买，平台则会提高收益分成比例来保障自身利益。

4 均衡策略分析

4.1 策略选择

本节通过比较转售模式和代理模式下电商平台的利润，分析电商平台的最优销售模式以及其对制造商的影响。我们根据电商平台和制造商在不同销售模式下的利润变化，给出四个区间，Ω1,Ω2,Ω3,Ω4。

由于电商平台处于绝对领导地位，它会根据自身利润情况决定提供转售模式还是代理模式，但对于制造商来说，它只能被动接受电商平台提供的销售模式，即使这种模式可能会损害它的利益。

当{β,γ,φ}∈Ω1,Ω2时，电商平台会选择转售模式，但是制造商只有当{β,γ,φ}∈Ω1时才会偏好转售模式，反之，当{β,γ,φ}∈Ω2时，制造商偏好代理模式。同理，当{β,γ,φ}∈Ω3,Ω4时，电商平台会选择代理模式，而制造商只有在{β,γ,φ}∈Ω4时，才会偏好代理模式。综上所述，Ω1,Ω4为双赢区间，平台选择模式和制造商偏好模式相同;Ω2,Ω3内平台选择模式和制造商偏好模式不同，无论平台如何选择，都会损害制造商利益。基于此，可以得到如下几个推论：

推论3存在β1(γ,φ)<β2(γ,φ)，当β<β1(γ,φ)时，{β,γ,φ}∈Ω4，即Πr<Πm,πr<πm；

当β1(γ,φ)<β<β2(γ,φ)时，{β,γ,φ}∈Ω3，即Πr<Πm,πr>πm；

当β>β2(γ,φ)时，{β,γ,φ}∈Ω1，即Πr>Πm,πr>πm。

由推论3可以看出，存在β1(γ,φ)，当β<β1(γ,φ)时，电商平台会提供代理模式，制造商也偏好代理模式。随着β增加，存在β2(γ,φ)，当β1(γ,φ)<β<β2(γ,φ)时，制造商转而偏好转售模式。β继续增加，当β>β2(γ,φ) 时，平台提供转售模式，此时制造商也偏好转售模式，两者实现双赢。

推论4存在γ1(β,φ)<γ2(β,φ)，当γ<γ1(β,φ) 时，{β,γ,φ}∈Ω1，即Πr>Πm,πr>πm；

当γ1(β,φ)<γ<γ2(β,φ)时，{β,γ,φ}∈Ω3，即Πr<Πm,πr>πm；

当γ>γ2(β,φ)时，{β,γ,φ}∈Ω4，即Πr<Πm,πr<πm。

由推论4可以看出，存在γ1(β,φ)，当γ<γ1(β,φ)时，电商平台会提供转售模式，与制造商的偏好相同。随着γ增加，存在γ2(β,φ)，当γ1(β,φ)<γ<γ2(β,φ)时，平台提供代理模式，然而制造商依然偏好转售模式。当γ继续增加到γ>γ2(β,φ)时，平台提供代理模式，此时与制造商偏好相同。

推论5存在φ1(β,γ)<φ2(β,γ)，当φ<φ1(β,γ)时，{β,γ,φ}∈Ω4，即Πr<Πm,πr<πm；

当φ1(β,γ)<φ<φ2(β,γ)时，{β,γ,φ}∈Ω3，即Πr<Πm,πr>πm；

当φ>φ2(β,γ)时，{β,γ,φ}∈Ω1，即Πr>Πm,πr>πm。

由推论5可以看出，存在φ1(β,γ)，当φ<φ1(β,γ)时，电商平台提供代理模式，制造商也偏好代理模式。随着φ增加，存在φ2(β,γ)，当φ1(β,γ)<φ<φ2(β,γ)时，制造商转而偏好转售模式。φ继续增加，当φ>φ2(β,γ)时，平台转而提供转售模式，同时制造商也偏好转售模式。

除此之外，还存在Ω2={{β,γ,φ}|Πr>Πm,πr<πm}，当{β,γ,φ}∈Ω2时，Πr>Πm,πr<πm。但满足Ω2成立的条件很苛刻，不在讨论范围内。

4.2 数值算例

由于利润函数的复杂性，均衡策略难以得到显式结果，因此本文接下来采用数值模拟的方法，分析需求对销售价格的敏感程度β，需求对退货价格的敏感程度γ，退货量对退货价格的敏感程度φ对平台和制造商销售模式选择的影响。

4.2.1 需求对销售价格的敏感程度对策略选择影响

首先分析需求对销售价格的敏感程度β对平台和制造商销售模式选择的影响，β越大，价格变化对需求的影响也越大，由推论1和2可知，β增加会导致销售价和退货价的降低，这会对平台和制造商利润带来相反的影响。假设α=1500,φ=100,γ=14,φ=2，数值模拟结果如表1所示5。

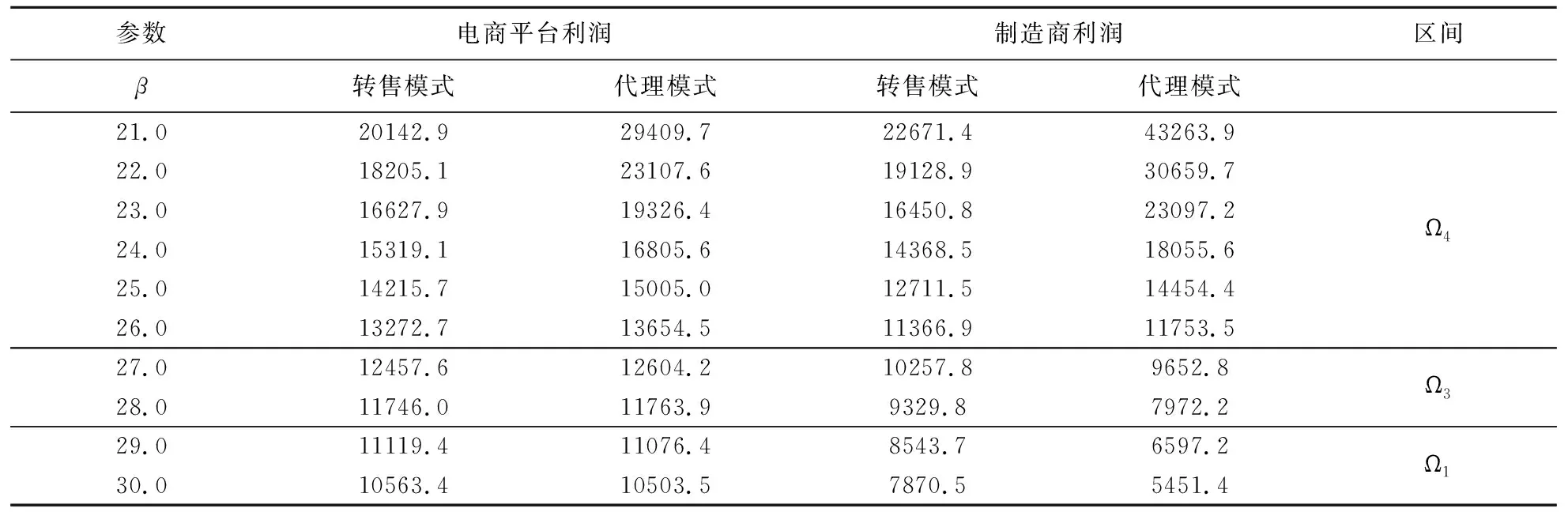
表1 需求对销售价格的敏感程度对利润的影响

当β较小时(β<β1(γ,φ))，平台在代理模式利润更高，因此会选择代理模式。因为当β较低时，商家可以制定较高价格来获取更高收益，同时为了吸引消费者也会提供较高退货价。此时平台如果提供代理模式，不需要平台自己采购产品销售和处理退货，只需要提供服务就可以获得较高的利润，同时，因为制造商的产品售价高，平台收取的分成比例较低，因此制造商也会偏好代理模式。当β居中时(β1(γ,φ)<β<β2(γ,φ))，市场需求的价格敏感程度提高，代理模式下，制造商无法通过制定高价获利，因此会选择降低价格，利润空间变小，这就导致制造商转而偏好转售模式。当β较大时(β>β2(γ,φ))，消费者对价格的敏感度较高，而对退货价的敏感度不高，因此需要提供较低的产品价格来刺激需求，提供较低的退货价来减少损失。此时平台会选择转售模式，掌握产品价格和退货价的决策权，实现利益的最大化，同时，制造商不需要处理退货，也能一定程度降低损失，因此也会偏好转售模式。表1的数值结果与推论3一致。

4.2.2 需求对退货价格的敏感程度对策略选择影响

需求对退货价格的敏感程度γ越大，退货价格变化对需求的影响也越大，由推论1和2可知，γ增加会导致销售价和退货价的增加。销售价的增加会给企业带来更高的边际收益，但是退货价的增加会抑制这种影响。假设α=1500,φ=100,β=14,φ=2。

与4.2.1节的数值结果类似，数值结果与推论4一致。需求对退货价格的敏感程度γ会影响平台(转售模式)和制造商(代理模式)的价格决策和退货价决策，进而影响两者在不同销售模式下的均衡利润，使得随着γ的增加，平台和制造商都会从转售模式向代理模式转变，但是两者转变的节点是不同的。

4.2.3 退货量对退货价格的敏感程度对策略选择影响

最后分析退货量对退货价格的敏感程度φ对平台和制造商模式选择的影响，φ越大，退货价格的变化对退货量的影响也越大，由推论1和2可知，φ增加会导致退货价的降低。假设α=1500,φ=100,β=15,γ=12。

与4.2.1节的数值结果类似，表3的数值结果与推论5一致。退货量对退货价格的敏感程度φ与需求对销售价格的敏感程度β影响类似，当φ较小时，企业可以制定较高的退货价刺激需求，但是也会带来较高的退货量，因此平台会选择代理模式，规避退货带来的不良影响，同时要求较低的利润分成比例，这促使制造商也会偏好代理模式。随着φ增加，企业难以制定较高的退货价来刺激需求，因此平台因为规避退货而选择代理模式的动机减弱，使得平台转向转售模式，掌握产品价格和退货价的决策权，从而实现利润的优化。

5 结论

在网络购物中，消费者退货是影响商家经营的重要因素之一。由于无缺陷退货在退货中占比较大，且在不同销售模式中对于无缺陷退货产品的处理方式不同，本文考虑由一个制造商和一个占据绝对领导地位的大型电商平台组成的供应链，建立并分析了电商平台和制造商的定价策略与退货策略的联合决策模型。具体来说，消费者的需求取决于销售价格和退货价，消费者的退货取决于退货价。在此基础上，本文研究了在转售和代理这两种销售模式下电商平台和制造商的最优决策，并分析平台的最优销售模式选择，及其对于制造商的影响。通过模型推导和数值模拟分析，得出以下结论：

首先，在不同销售模式下，最优定价和退货政策是相互依存的。当产品的销售价格较高时，商家应该提供宽松的退货政策(即退货价较高)，这也能起到信号传递的作用，让消费者对产品质量等方面更加信任，也更容易接受较高的销售价格。反之，当产品售价较低时，商家应该提供较低的退货价格来减少消费者退货，获得更高收益。

其次，电商平台和制造商的定价和退货政策取决于消费者的敏感类型。当消费者需求对销售价格敏感时，商家应该采用低价策略来增加需求，同时降低退货价格。然而，当消费者需求对退货价格敏感时，商家可以采用高价策略并提供宽松的退货政策，以吸引更多消费者购买。当消费者退货对于退货价格敏感时，商家应降低退货价和售价，进而降低处理退货的成本。

最后，通过比较平台在不同销售模式下的利润，可以得到电商平台的最优销售模式选择，以及最优销售模式选择对制造商收益的影响，这些也与消费者的敏感类型有关。当需求对价格的敏感程度较低、需求对退货价格的敏感程度较高及退货量对退货价格的敏感程度较低时，平台应该提供代理模式，反之提供转售模式对平台更有利。通过分析可知，当平台处于绝对领导地位且满足特定条件时(Ω1,Ω4)，平台的策略选择对于制造商是有利的，两者能够实现共赢。由于制造商只能被动接受平台提供的销售模式，因此在某些特定情形下(Ω2,Ω3)平台的最优策略会损害制造商的利益。

在本文的研究中，我们没有考虑产品残值，并且认为消费者对于不同销售模式下产品的满意度是一致的，但现实中对于不同渠道下购买的产品，消费者的满意度可能不同，这也是未来值得研究的方向。