改进的蝗虫优化算法在双目标应急物资中心选址问题中的应用
2022-05-14彭大江叶春明赵灵玮
彭大江, 叶春明, 赵灵玮
(上海理工大学 管理学院,上海 200093)
0 引言
近年来,国内外频发地震、海啸和瘟疫等紧急事件,它们不仅影响面积广,而且无法做到全面预防,还会造成巨大的人员伤亡和经济损失[1,2]。当此类紧急事件发生时,如何能在短时间内迅速响应,做到有条不紊地展开救援和收集发放物资是应急管理领域中的研究重点[3,4]。以2020年初爆发的新型冠状病毒为例,武汉市在这场战役中做出巨大牺牲:临时封城,关闭通往其他地区的通道,坚决防止疫情向其他地区扩散。在这种情况下,疫区人民的生活及医疗物资极度匮乏,急需临时建立应急物资仓库,收集国家政府为疫区输送的物资和社会爱心人士自发捐赠的物资,然后高效合理地分发给群众[5]。合理的应急设施布局不仅会稳定民心,使得防控过程更加顺利,并且在后续的物资运输分配过程中按需分配,更加公平。
目前国内外研究的应急选址问题主要基于三类经典模型:(1)选择设施并适当分配给需求点使得需求点与设施之间最大服务距离最短的p-中心问题;Lu在此基础上考虑点权重和不确定救援需求与配送时间,利用改进的模拟退火算法求解[6];Ye等在此基础上考虑人口分布,经济条件等因素利用变邻域搜索算法来求解应急仓库的选址问题[7]。(2)在覆盖所有需求点的前提下,使选择设施的数量最小化的集合覆盖问题,或是在给定设施数量的前提下,使选择设施能覆盖尽可能多的应急点的最大覆盖问题;陈志宗等以此为基础提出了一种灾害应急反应的枢纽集覆盖模型,并运用改进的遗传算法求解[8]。(3)选择设施使需求点到对应设施的加权平均距离最小化的p-中值问题;Zhao等在此基础上考虑地震时的撤退时间与总庇护区域进行建模,并用改进的粒子群算法求解[9];陈刚等在传统p-中值问题上运用多项logit模型刻画居民的有限理性选择行为,分别使用遗传算法和模拟退火算法求解此情况下的应急避难所选址问题[10]。
这几类选址问题均为离散选址问题,考虑应急点的需求,在待选设施中进行选择。现已证明,三类选址问题均为NP-Hard,除非P=NP,否则该类问题不存在多项式时间精确算法。目前解决该问题的算法主要集中在两类:以割平面法和分支定界法为代表的精确算法[11,12]〗。此类算法的优势在于保证获得全局最优解,但由于其时间复杂度为指数级,无法应用到大规模问题中。另一类为群智能优化的启发式算法[7~9]。此类算法虽然无法保证获得理论全局最优,但可在合理计算时间内获得高效的满意解,因此更适合用于实际应用中较大规模的问题。此外越来越多的学者考虑更贴合实际情况的多目标应急选址问题[13~15],而这类问题的求解方式通常与智能优化算法更加契合,因此许多研究采用此类算法求解以获得更佳的解决方案。
本文在已有文献的研究基础上,在考虑后续运输成本和有概率发生紧急事件而导致无法正常运送物资的情况,为应急物资中心选址问题建模;然后针对该问题,引入并改进蝗虫优化算法[16],使其更适合于求解该应急物资中心选址问题;最后通过数值计算的对比实验,验证该算法的可行性和有效性。
1 问题与模型
1.1 问题描述
当区域内发生紧急事件后,物资和人手极度匮乏,若建立过多的应急物资服务点不仅会导致资源浪费,更重要的是很可能导致外部物资运送到该区域时分配效率低,转运速度慢,难以高效保障生活医疗水平。在这种情形下,需要在区域内选择数个设施作为应急物资中心,来提高外界物资分配至该区域内各需求点的效率和仅存资源的利用率。因此问题描述为区域内存在m个应急需求点,要求在n个给定的设施中,确定p个设施作为应急物资中心点,使得一些指标最大化或最小化。
对于应急物资中心选址问题,若完全考虑所有细节会使模型过于复杂,为突出研究的重点同时保证模型的扩展性,我们做出如下假设:(1)应急物资中心的储备量由其服务的需求点确定,即应急物资中心不会出现物资供给不足的情况;(2)每个应急需求点接受且仅接受某一个应急物资中心点的服务;(3)每个应急需求点有出现紧急情况的概率。当某个应急点出现紧急情况时,其必须处于对应应急物资中心的最大正常服务半径内方可正常接受服务。
在如上假设的前提下,我们以最大覆盖选址模型为基础,建立双目标覆盖模型来抽象应急物资中心的选址问题,以达到如下目标:(1)最小化应急需求点到相应应急物资中心的运输成本;(2)最小化出现紧急情况时无法正常完成运输的物资量。基于以上分析,我们定义以下数学符号并建立该数学模型。
1.2 数学模型建立
双目标覆盖模型可用一个二分图G=(E,F)来描述,模型中涉及的数学符号及意义如下:
E={ei|i=1,2,…,m}:应急需求点集合,共m个应急需求点;
F={fj|j=1,2,…,n}:候选应急物资设施点集合,共n个候选设施点;
ωi:需求点ei的物资需求量(ωi>0);
p:开设的设施点数量(p d:规定设施点可以正常服务的最大距离; dij:需求点ei到设施点fj的欧氏距离; A=[aij]m×n:若dij xj∈{0,1}:若设施点fj开设,xj=1,否则xj=0; yij∈{0,1}:若需求点ei接受设施点fj的服务,yi=1,否则yi=0; δ:运输成本系数(δ>0),即运输每单位距离的每单位物资将消耗δ单位的运输成本; μ:发生紧急情况的概率(μ>0)。对于满足yij=1的设施点fj和需求点ei,若dij>d则发生紧急情况时,设施点fj无法正常服务需求点ei。 根据上一节目标函数与约束条件的分析,建立的双目标覆盖模型的数学表达式如下: (1) (2) (6) 目标函数(1)表示需要最小化所有被覆盖需求点到对应设施之间的运输成本总和;目标函数(2)表示需要最小化无法正常配送的物资量的期望值;约束(3)表示选择的设施点数应正好为p个;约束(4)表示需求点ei可接受fj服务的必要条件是设施点fj开设;约束(5)表示每个需求点接受且仅接受1个设施点的服务;约束(6)表示xj和yi均为0-1变量。 蝗虫优化算法(Grasshopper Optimization Algorithm, GOA)是Saremi等人[16]于2017年提出的一种新型群智能优化启发式算法,其源于对大自然中蝗虫群的觅食行为模拟。蝗虫优化算法有收敛速度快,原理简单易实现的优点,但其全局搜索能力一般,不易搜索到最优解。针对这些问题,有学者对算法寻优能力其进行改进[17,18]。同时GOA在优化中的应用也比较广泛,目前有函数优化[19,20],作业车间调度[21],特征提取[22],背包问题[23]等。 由于篇幅原因,此处不再赘述基本蝗虫优化算法的流程,具体请参见文献[16],个体位置更新公式如下所示: (7) (8) 为将蝗虫优化算法应用到本文的应急物资中心选址问题,需要修改以下三个方面才能使其正常运行:(1)初始化的操作;(2)修复不满足约束条件的解;(3)修改更新公式。 2.2.1 初始化操作 算法中解的维度与待选设施点数n相同,一个满足约束条件的解中有且仅有p个设施点开启,为保证初始化效率和解的多样性,我们采用随机初始化的方式。构造解x的主要操作步骤如下: 1)记当前已开设设施点数为k=0,当前处理的设施标号i=1; 3)若k 2.2.2 修复解的操作 对于不满足约束的解x,记其中已开设设施数为k,分以下三种情况处理: 1)若k=p,无需修复,结束操作; 2)若k 3)若k>p,在已开设设施中随机选择k-p个关闭,标记对应的xi=0。 2.2.3 修改更新公式 为在二进制蝗虫优化算法中延续原算法中按全局最优解更新位置的思想,我们改进更新公式,替换为如下操作: (9) (10) (11) 为将算法应用于本文问题,我们需要设计二进制多目标蝗虫优化算法(Binary Multi-objective Grasshopper Optimization, BMOGOA),考虑首先引入Fuzzy集关联熵系数[24]来建立目标函数值评价体系,然后加入外部档案来存储非劣解,再提出根据关联熵系数来动态确定每轮迭代中最优解的方法,使算法可以正常迭代,最后添加竞争决策机制对算法寻优能力进行改进。 关联熵系数是评价两个Fuzzy集之间相似性的重要工具,其计算的主要步骤如下: 1)对两个Fuzzy集A和B,它们各自的熵计算方式如式(12)和(13)所示: +(1-A(xi))ln(1-A(xi)) (12) +(1-B(xi))ln(1-B(xi)) (13) 其中,n是Fuzzy集中元素的个数,A(xi)和B(xi)分别表示Fuzzy集A和B中的第i个元素对相应Fuzzy集的隶属度,本文中可简单理解其为成员值,满足O 2)A关于B的偏熵记为EB(A),对应的,B关于A的偏熵记为EA(B),计算方式如下: +(1-B(xi))ln(1-A(xi)) (14) +(1-A(xi))ln(1-B(xi)) (15) 3)A与B之间的关联熵定义如式(16)所示,为它们的偏熵之和: E(A;B)=EB(A)+EA(B) (16) 4)A与B之间的关联熵系数定义为式(17)所示: (17) 记两个单目标函数最小值构成的向量为Zmin={z1,min,z2,min},单目标函数最大值构成的向量Zmax={z1,max,z2,max},算法中种群X的第i个个体xi,其实际函数值序列为Zi={z1(xi),z2(xi)},我们采用以下方式构造解的关联熵系数: (18) 个体xi的第j个目标函数值映射到Fuzzy集后成员值为fj(xi),其满足0 为尽可能获取帕累托前沿,我们为算法添加外部档案[25],存储每一代新产生的非劣解。 3.3.1 外部档案初始化 记初始种群为X,外部档案为EA。由帕累托支配的定义可知,与理解函数值序列Zmin={z1,min,z2,min}对应的解x1,min和x2,min大概率不被当前种群中的解支配,因此我们将其添加至外部档案。外部档案初始化过程的伪代码如算法1所示。 3.3.2 外部档案更新 算法执行过程中,种群每次完成迭代,都需要对外部档案进行更新,更新过程伪代码如算法2所示。 算法2.外部档案更新的伪代码输入:种群X,外部档案EA,1.初始化临时种群tX=X2.while tX≠{}3.令x*=tX,执行tX=tX{x*}4.记is_dominated=False5.for each a in EA6.if x*≻a then7.执行EA=EA{a}8.continue9.else if x*p x then10.is_dominated=True11.end if12.end for13.if not is_dominated=then14. EA=EA U{x*}15.end if16.end while 二进制蝗虫优化算法的更新过程需要当前最优解,若在多目标的情况下,直接将解的关联熵系数最大的作为最优解,则导致最终的解将大概率聚集于一点,不可能逼近帕累托最优解。因此,本文提出基于轮盘赌算法的最优解选择策略,其主要步骤如下: 1)对外部档案EA中的每个非支配解计算解ai的关联熵系数fi; 3)产生一个[0,1]内均匀分布的随机数r,若r 上述操作完成后,可按与关联熵系数成正比的概率从外部档案EA中获得一个非支配解,从而在迭代过程中动态引导种群向帕累托前沿靠近。 为增强多目标蝗虫优化算法在离散空间的搜索能力,我们为算法添加竞争决策机制[26]。该机制在迭代次数l>λLmax(0<λ<1)时被执行。竞争决策机制的伪代码如算法3所示。 如图1所示是算法的执行过程图,算法开始后,首先建立两个较小的种群,并分别调用单目标的二进制蝗虫优化算法并行计算,记录好函数上下界后才开始正式计算。 图1 多目标蝗虫优化算法流程图 为验证多目标蝗虫优化算法在应急物资中心选址问题上应用的可行性和有效性,本节开展数值实验,并通过一些指标来评估算法的性能。作为对照,本文选用多目标离散选址问题中使用频率最高的NSGA-II算法,该算法是目前公认最有效的多目标进化算法之一,通过对比实验评测本文算法性能。 本文的测试数据选择OR-Lib中最大覆盖问题的3个SJC数据集,其中仅给出应急需求点的坐标和对应的需求量,急物资中心可选址在任意需求点。由于给定的开设数p和最大正常服务距离d的取值不同将产生完全不同的问题,我们最终选择的数据集为SJC324,SJC500和SJC818,其应急点数分别为324,500和818。该数据集中没有运输成本系数δ和发生紧急情况的概率μ的信息,为模拟实际情况,我们取δ=0.01,μ=0.1。 由于无法获取该问题的真实帕累托前沿,为评测算法的解集质量,计算效率和鲁棒性,我们主要通过以下指标来评价算法的性能。 (1)非支配解的数量(Number of Pareto Solution, NPS)是算法获取的非支配解数量,一般认为非支配解数量越多,算法性能越好。 (2)空间评价指标(Spacing Metric, SM)衡量帕累托近似解集中每个解到其他解的最小距离的标准差,反映解集中解分布的均匀性,其计算公式如式(19)所示: (19) (3)C指标(C-Metric)可衡量非支配解集A和B中占优支配的情况,计算方式如式(20)所示,其表示B中个体被A中个体支配的占比。 (20) C(A,B)的取值范围是[0,1],特别地,如果C(A,B)=1表示B中所有个体均被A中某些个体支配;如果C(A,B)=0表示B中所有个体都不被A中任何个体支配。 多目标蝗虫优化算法的关键参数设置:作用力函数s(r)中l=1.5,f=0.5、保留最优解概率的边界值rmin=0.45,rmax=0.95、目标函数值的边界系数α=0.8,β=1.2以及调用竞争决策机制的迭代数比率λ=0.8;NSGA-II的交叉概率为0.9,变异概率为0.1。两种算法的种群数量均为为300,在BMOGOA开始时分别分配50个个体作为2个单目标函数优化过程的种群,多目标优化过程仅使用200个个体。由于问题规模相对较大,两种算法的最大迭代次数均设置为300次。本文的实验环境为Intel Core i5 2.3Ghz,16GB内存,Windows 7操作系统。为保证公平性,多目标蝗虫优化算法和NSGA-II算法均使用C++编写。 我们记BMOGOA为算法A,NSGA-II为算法B,各算法独立求解每个问题10次以后,各自合并非支配解集,得到的算法的性能指标如表1所示。 表1 算法性能指标统计表 从表1可以看到,BMOGOA在测试问题中指标几乎全面优于NSGA-II。对比图2和图3可发现,保持数据集和正常服务距离不变,当待选应急物资中心数增加时,BMOGOA较NSGA-II表现更佳:求得的解有良好的分布,并且计算时间较NSGA-II平均降低24%,在大规模问题中的求解过程中响应更加迅速。纵观所有测试数据,BMOGOA获得的解都不劣于NSGA-II获得的解,因此说明本文算法的在较大规模问题上的可行性和有效性。 图2 问题8的非支配解集分布 本文对应急物资中心选址问题进行研究,提出了一种考虑后续运输成本以及紧急情况下不能正常配送物资的离散选址模型,针对该模型提出了一种二进制多目标蝗虫优化算法(BMOGOA)。该算法以模糊关联熵为核心,融合竞争决策机制和最优解选择机制,引导算法不断向理想解迭代更新,同时存储当前非劣解到外部档案。通过多次数值实验,BMOGOA表现出较强的可行性和有效性,并在测试问题上几乎全面优于目前多目标离散选址问题中使用频率最高的NSGA-II,展现出更高的求解效率,同时能求得更优质的解,因此其可作为求解多目标离散选址问题的一种有效算法。在实际生活中不乏中大规模的离散应急选址问题,通过对本文模型的扩展和算法的优化,能在可接受时间范围内提供数个较优质的解以供决策人选择,在此基础上结合定性分析,可在应急物中心资选址问题中做出更科学的决策,最大化仅有资源的利用率。2 改进的蝗虫优化算法
2.1 基本蝗虫优化算法
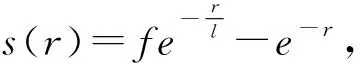
2.2 二进制蝗虫优化算法
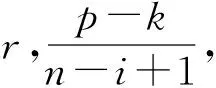
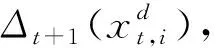
3 新型多目标蝗虫优化算法
3.1 Fuzzy集的关联熵系数

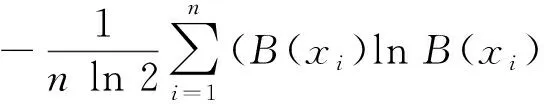
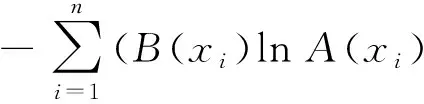
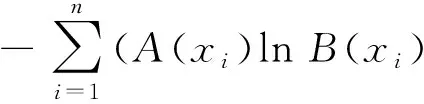

3.2 解的关联熵系数
3.3 多目标更新策略


3.4 最优解选择策略
3.5 竞争决策机制

3.6 多目标蝗虫优化算法执行流程
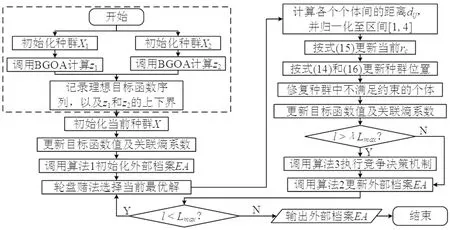
4 数值实验及结果分析
4.1 实验数据
4.2 评价指标
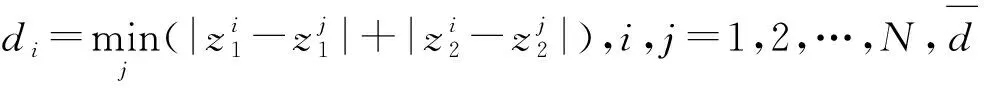
4.3 参数设置
4.4 计算结果与分析


5 结论
