供应商不确定情景下药品物流多中心选址优化研究

袁志远, 高 杰, 杨才君

(1.西安交通大学 管理学院,陕西 西安 710049; 2.西安交通大学 药学院,陕西 西安 710061)

0 引言

2018年12月6日，第一批国家组织药品带量集中采购中标结果揭晓。2019年12月，第二次集中采购推广至全国，集采中标品种32个，122家企业参与招标，最终中选企业77家。多个品种第一次集采中标的企业，在第二次集采中却未能中标。可以看到，药品集中采购由国家顶层设计并组织实施，未来或将成为公立医疗机构采购药品的主流模式。集中带量采购每年开展一次，而中标的药品生产企业每年都可能发生变化，供应商的不确定性成为当前药品物流中心选址面临的新问题。

针对物流中心选址，已有研究主要围绕需求不确定以及配送过程不确定展开。需求不确定方面，如周愉峰等[1]为了规避应急条件下的不确定风险，构建了国家血液战略储备库选址-库存问题的随机p-鲁棒优化模型；迟伊宁[2]综合考虑物流成本和碳排放量最小两个目标，建立需求不确定条件下的多目标鲁棒优化模型；陈希等[3]在医疗中心动态选址中考虑了需求的不确定性，采用基于隶属度函数的加权方法求解得出医疗中心选址与分配方案；苑敬云[4]针对需求不确定下的中心选址问题，构建了加入决策偏好的冷链物流中心选址多目标优化模型；梁希[5]在考虑碳排放成本情况下，构建了需求不确定下的低碳配送中心选址模型。这些研究主要是针对需求不确定的情况下中心选址的研究，而针对供应商不确定的情况下，中心选址的研究很少涉及。由于食品和医药物流涉及到易腐易烂问题，现有研究多在传统模型的基础上增加时间约束，或提高运输成本(制冷成本、货损成本、碳排放成本等)。如王晶等[6]针对应急资源配送路径问题，构建了应急设施定位、障碍道路修复以及配送路径选择的综合优化模型；邹建城[7]构建考虑碳排放因素综合配送成本最小以及顾客满意度最大的生鲜农产品冷链配送路径优化模型；陶帝豪等[8]综合考虑车辆固定成本、燃油成本、货损成本及碳税成本，构建了成本最小目标数学模型；Bayan Hamdan等[9]针对灾后血液供应链中断风险，为最大限度地减少灾难发生后向医院运送血液的时间和成本，构建了一个双目标稳健优化模型。

综合国内外文献，无论是传统的物流中心还是针对食品和医药的物流中心，目前都没有针对供应商不确定的情况下，物流中心选址的研究。由于药品物流配送中心技术含量高，配送时效性强，质控要求高等特点，传统物流和普通冷链物流很难达到药品物流配送的要求。因此，在全国药品集中带量采购的背景下，构建新的药品物流中心，并考虑供应商的不确定性，成为一个全新的研究问题。

本文基于全国药品集中带量采购这一背景，针对药品供应商不确定情景下的药品物流中心选址问题，建立整体成本最优的选址模型，设计多阶段改进禁忌搜索算法对其求解。

1 供应商不确定情景下的第四方药品物流多中心选址优化模型

我们假定：1)同一种规格的药品有多家生产企业参与竞标，生产企业h生产的f种药品未来三年的中标概率为phf；2)共有J个备选城市可建立物流中心，第j个城市至多建立一个物流中心；3)需求城市I个，需求城市i未来三年的药品f销售量估计为qif；4)生产企业到物流中心，以及物流中心到需求城市之间可由多个第三方物流企业承担运输服务。

1.1 药品物流中心选址优化模型

根据4+7带量集中采购招标评审标准对国内近年来药品生产企业生产质量、供应能力、国家基本要求和同类药品参标中标次数等数据进行梳理和分析，建立药品供应商不确定情景下物流整体费用最小的中心选址模型。物流整体费用包括药品运输成本，中心建设成本，药品在中心装卸转运成本等。

该问题需要的基本标记符号、参数和决策变量采用如下记号：

基本标记符号和参数：

决策变量：

xijf:如果第j个物流中心为第i个城市配送f种药品，则xijf=1；否则，xijf=0；

yj:如果城市j建立物流中心，则yj=1；否则，yj=0。

考虑未来三年的需求，建立如下的药品物流中心选址模型：

(1)

(7)

约束(2)表示仅有一个物流中心给第i个需求城市配送f种药品；约束(3)表示第j个物流中心给第i个需求城市配送第f种药品的前提是第j个城市要建立物流中心；约束(4)表示至少建设1个药品物流中心；约束(5)表示企业h生产的f种药品运输到各物流中心的总量等于h企业生产的f种药品预测中标量；约束(6～7)表示决策变量均为0-1整数变量。

1.2 药品生产企业中标概率预测

依据药品带量采购评审标准和药品生产企业投入的持续性和生产的连贯性，结合大数据预测概率计算公式[10～13]，药品生产企业未来3年中标概率预测模型建立如下:

(8)

其中变量含义如下：

Lhf：药品生产企业h生产的f种药品近5年的中标次数

2 求解算法

2.1 求解思路

根据模型组成结构，此模型属于选址-分派问题，选址-分派问题已被证明属于NP难题[14]。为了提高搜索的精度，避免陷入局部最优，本文采用多阶段改进禁忌算法进行求解[15～19]。根据模型组成将求解过程分为三个阶段，第一阶段寻找配送F种药品从备选物流中心到需求城市每种配送方案的最小费用(包括物流中心到需求城市的运输费用和装载费用)；第二阶段寻找F种药品从生产企业到备选物流中心每种配送方案的最小费用(包括生产企业到物流中心的运输费用和卸载费用)；第三阶段寻找完成F种药品物流服务的整体费用最小的物流中心及物流方案。

2.2 TS编码

药品f，药品生产企业h，备选物流中心j，第三方物流企业v、u，运输方式n、m和需求城市i为本模型变量。由于数组元素访问方便且不易混淆，本文用数组来表示禁忌算法的每个解，数组中每个确定位上的元素值为各变量f、h、j、m、n、v、u、i的取值。

第一阶段物流中心到需求城市的TS编码示意如图1所示。例如(8，9，5，1，2)表示第8种药品，从物流中心9到需求城市由第5家第三方药品物流采用第1种运输方式。

图1 第一阶段TS编码示意图

第二阶段生产企业到物流中心的TS编码示意如图2所示。例如(9，7，3，2，5)表示第9种药品，第7家生产企业，备选物流中心5作为物流中心，企业到物流中心由第3家第三方药品物流采用第2种运输方式。

图2 第二阶段TS编码示意图

2.3 算法设计

第一阶段：寻找F种药品从备选物流中心到需求城市每种配送方案的最小费用

1)随机选择初始解

利用随机策略选用初始解，如(3，7，5，2，1)表示第三种3药品，从物流中心7到需求城市1由第5家第三方药品物流采用第2种运输方式。

2)邻域边际搜索

根据变量f,i,j的取值范围，按照邻域边际搜索原则进行搜索，得到新的解。

3)邻域内搜索

把f,i,j的值与禁忌表进行比较，如果禁忌表中存在与当前f,i,j取值相同的解返回2)，如果不同，搜索邻域内的解。

4)寻找邻域内最优解

首次领域内搜索，把邻域内搜索到的所有解分别代入评价函数进行比较，找出评价函数最小的解，记忆最优的第三方物流和运输方式，下次邻域内搜索直接采用首次记忆最便宜的第三方物流和运输方式，不再进行别的搜索。

5)把邻域内最优解存入禁忌表

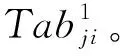
6)终止条件判断

如果迭代次数iter⟸max-iter(最大迭代次数)，则转 2)；否则，终止算法。

7)输出第一步结果

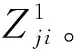
(9)

第二阶段：寻找F种药品从生产企业到备选物流中心每种配送方案的最小费用

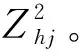
(10)

第三阶段：寻找F种药品物流整体费用最小值及最优配送方案。

1)寻找每种配送方案药品物流整体费用最小值

根据第一阶段、第二阶段得到的结果和建设物流中心固定成本，寻找f种药品配送方案整体物流费用最小值Zf(x,y)。

2)寻找药品物流整体费用最小值

把各种配送方案得到的药品物流整体费用最小值进行比较，选择配送所有药品物流整体费用最小的方案作为最优方案，并记录物流中心、各段配送企业、各段配送方式及整体最优值。

3)输出完成F种药品物流服务整体费用最小值及物流方案

输出minZ(x,y)和费用最优方案。

3 算例

本文选择2018年4+7带量采购25种药品中的“厄贝沙坦氢氯噻嗪口服常释剂型”、“阿莫西林口服常释剂型”，“头孢呋辛酯口服常释剂型”药品为例分别用1、2、3代码表示，假设参与这三类药品招标的药品企业中标概率和药品企业到备选中心距离如表1，备选中心到各需求城市的距离如表2，其中前4个城市为直辖市，后7个为副省级中心城市。为更好的实现药品带量集中采购物流服务，某第四方药品物流规划选择2个地点建设2个物流中心。在不知道未来3年内那几家药品生产企业中标，通过相关数据收集整理仅知道生产同类药品企业最近5年参标结果和各药品生产企业质量、供应能力、基本资质等相关信息。某第四方药品物流该如何决策规划？

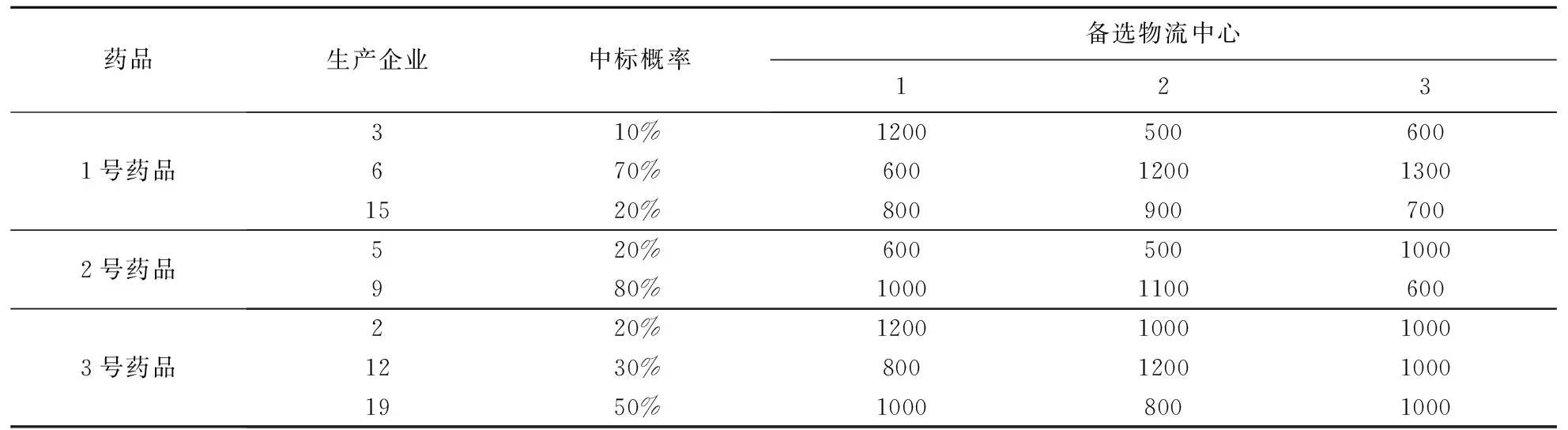
表1 药品的生产企业和各备选物流中心距离(千米)

表2 需求城市到备选物流中心的距离(千米)

根据2018年各药品带量集中采购数量，推测未来三年11个城市对1号药品共需45吨，2号药品共需45吨，3号药品共需28吨，各直辖市对三种药品需求量分别为6,6,3.5吨，7个副省级中心城市对三种药品需求量分别为3,3,2吨。第三方药品物流运输费用如表3，交通工具装卸费用如表4。企业到备选中心有汽车、火车、飞机3种运输方式分别用1、2、3表示，备选中心到需求城市有汽车、火车2种运输方式分别用1、2表示，每个中心建设成本20万。

表3 第三方药品物流单位距离运输费用(元/吨)

表4 交通工具装卸费用(元/吨)

本文TS采用C++开发，其测试与运行均在CPU为2.5G、内存为8G和win 10操作系统环境下进行，最大迭代次数100次。运算结果如表5。

表5 运算结果

经过计算我们可得选择1号，2号，3号，1、2号，2、3号，1、2、3号备选物流中心的整体最优费用如表6。我们发现选择1，3号建设物流中心的整体最优费用小于其它任何一个方案的整体最优费用。表明该模型和算法能够优化第四方药品物流未来物流中心选址。

表6 物流中心方案最优费用(万元)

4 灵敏度分析

4.1 药品生产企业中标概率变化灵敏度分析

我们以算例中生产1号药品的企业中标概率的变化对物流中心选址的影响进行分析，不同情景下1号药品生产企业中标概率如表7，不同情景下1号药品物流整体费用变化如表8，不同情景下的最优物流中心方案如表9，结合算例中表1和2，我们发现药品生产企业中标概率越大选择距离越远的物流中心整体费用越大，选择距离越近的物流中心整体费用越小。

表7 不同情景下1号药品生产企业中标概率

表8 不同情景下1号药品物流整体费用变化(万元)

表9 不同情景下1号药品物流的最优物流中心方案及费用(万元)

4.2 中心建设成本变化灵敏度分析

我们以算例进行分析，在物流中心建设成本变化情况下，最优物流中心方案如表10。我们发现当物流中心建设成本超过23.82万元时，选择单个物流中心为最优方案；当物流中心建设成本小于23.82万元时，选择两个物流中心为最优方案。

表10 物流中心建设固定成本变化情况下最优物流中心方案

5 结论

本文研究了4+7药品带量集中采购中药品供应商不确定情况下多中心选址问题。根据药品企业相关数据和国内药品招标相关数据，构建了药品生产企业中标预测模型，构建了第四方药品物流多种药品多中心选址模型，设计了多阶段禁忌搜索算法对模型求解，通过具体算例对模型和算法进行了验证，结果表明该模型和算法能够优化第四方药品物流多中心选址。本模型是供应商不确定情景下药品物流中心选址模型，没有考虑配送时间要求等。因而，综合考虑时效，第四方药品物流多种药品多中心选址将是作者下一步研究的内容。