基于SDN 的高性能QoS 保障低轨道卫星星间路由算法

王奎宇，宋晓勤，缪娟娟，张昕婷，雷 磊

（南京航空航天大学电子信息工程学院，南京 211106）

0 概述

随着经济全球化和全球信息化进程的加速，地面通信网络已经不能满足日益增长的用户需求，天地一体化信息网络将提供更多资源［1］。卫星通信是一种理想的远距离通信技术，不仅可以克服地理条件的局限性，而且可以提供廉价、持续、可靠的通信信道［2-4］。因此，将卫星网络的全球覆盖性、移动性和可扩展性的优势与地面网络的巨大传输能力和低时延的特点相结合来实现空天地一体化的信息网络成为迫切需要解决的问题［5-6］。但低轨道（Low-Earth Οrbit，LEΟ）卫星通信网络中的动态拓扑，不均匀的流量分布，有限的功率、存储和处理能力使得传统路由算法无法应用于低轨道卫星的星间路由，并且新兴的网络应用需求日益复杂多变，亟需设计有效和灵活的卫星通信网络管理方案［7-9］。为解决卫星网络中的这些问题，研究人员将注意力转向了软件定义网络（Software-Defined Network，SDN）。

SDN 是一种新的通信网络体系结构模式，简化了通信网络系统的管理方式，将传统网络的控制平面和数据转发平面分开［10-12］，实现了数据的集中控制处理和通信网络资源的优化和利用。文献［13］经过深入研究指出SDN 在通信网络集成方面具有很大优势，可以降低卫星机载处理成本以及整个卫星网络成本。文献［14］在SDN 框架上提出多路径传输控制协议（Transmission Control Protocol，TCP），并证明该协议显著提高了网络吞吐量，可防止切换过程中的传输中断。

在现有研究中，星间路由算法主要包括虚拟拓扑法、虚拟节点法、动态拓扑更新法3 类。虚拟拓扑法利用卫星星座运转的周期性和可预测性，将星座周期划分为若干个时间片［15］。卫星网络拓扑在每个时间间隔内均可以看作是静态的，屏蔽了卫星高速运动造成的拓扑变化。但大量的时间片导致了巨大的路由表，并占用了大量卫星的存储资源。虚拟节点法的每个区域对应一个具有唯一逻辑地址的卫星，该地址用于确定卫星的下一跳。当卫星移动到下一个区域时，逻辑地址也会随之改变，但会出现网络拥塞等问题［16］。动态拓扑更新法利用卫星交换网络状态信息，获取实时的拓扑结构计算路由表，能够实时响应卫星节点失效、链路拥塞等情况，但路由算法复杂度明显增加。

近年来，低轨道卫星路由技术受到越来越多的关注。文献［17］提出卫星切换方案，以确保通信链路的可靠性。该方案可以减少用户的接入延迟，保证通信的连续性，但没有分析卫星间通信链路的连续性和稳定性。文献［18］提出一种基于软件定义网络的频谱共享和流量分流机制，实现蜂窝网络的地面基站与星地通信波束群之间的合作与竞争，但在星间链路（Inter-Satellite Link，ISL）切换时会产生较大的性能波动，并且未对不同优先级的业务提供保证。文献［19］提出一种基于时间结构的增广路径搜索方法，用于计算三层异构卫星网络容量，然而该方法并没有考虑实时星间链路状态变化的优化问题。文献［20］构建了一个按需任务模型来描述网络动态特性和不同的任务需求，然后将QoS 支持问题变为基于图的最大流量问题，并提出一种QoS 支持路由策略，但该策略仅考虑了QoS 保障，未考虑节点负载均衡以及星间链路切换问题。

针对上述问题，本文利用SDN 网络架构管理和优化LEΟ 卫星网络通信系统，提出一种高性能QoS保障的LEΟ 卫星星间路由算法。针对通信链路状态信息和星间链路通断实时变化的问题，根据剩余链路持续时间定义星间链路生存时间，得出每条星间链路的稳定度，解决由于链路切换导致的业务路径重构问题。基于高轨道（Geostationary-Earth Οrbit，GEΟ）卫星得到的星间链路的流量状态，定义链路负载矩阵，给出星间链路负载度函数，并利用标签交换路径（Label Switching Path，LSP）集合得到每条路径的负载度，以避免节点拥塞，实现网络负载均衡。通过路径代价函数给出路由决策矩阵，根据用户对业务时延、带宽和丢包率的不同要求，将业务分为3 种类型，定义权重因子矩阵，根据不同业务类型的需求，分配不同的权重因子，保证用户的QoS 要求。针对瓶颈节点提出调整因子来减小其对路由算法的影响，并通过理论证明调整因子的有效性。

1 系统模型

1.1 网络架构

采用基于SDN 的卫星网络通信架构，该架构由用户层、控制层和数据层组成［21］，其中，用户层主要由各类地面用户终端组成，控制层主要由地面站、GEΟ 卫星和中轨道（Medium-Earth Οrbit，MEΟ）卫星组成，数据层主要由LEΟ 卫星组成，如图1 所示。采用SDN 将网络通信设备的控制面和用户面解耦，在逻辑上集中控制面，并提供网络可编程性以及简化的标准接口管理功能。通过控制层中的GEΟ 与MEΟ 监控LEΟ 的全局链路状态信息，由地面控制层完成路由计算以及流表的下发。在图1 中：GEΟ 卫星是控制卫星，负责监控星间链路状态信息；MEΟ为辅助卫星，辅助GEΟ 收集LEΟ 卫星的状态信息；LEΟ 是数据转发卫星。利用SDN 的可编程功能，GEΟ 可以轻松实现LEΟ 网络中转发规则的更新，从而保证较低的数据传输延迟和少量的资源消耗，实现卫星网络中的资源优化分配。

图1 卫星网络通信架构Fig.1 Communication architecture of satellite network

1.2 卫星模型

数据转发任务由低轨道卫星通信系统组成，包含NL×ML颗低轨道卫星，其中，NL表示星座轨道平面的个数，ML表示每个轨道包含的卫星颗数。每颗低轨道卫星用(i,j)进行编号，i代表卫星所处的轨道号(i=1,2,…,NL)，j为卫星所处轨道内的卫星编号(j=1,2,…,ML)。1 颗卫星的星间链路一般考虑为4 条，包括2 条相邻轨道的轨间链路和2 条同一轨道面的轨内链路。在一般情况下，可以建立两条连续的轨内链路，轨间链路则需要根据卫星的运动不断切换，并且在极地地区卫星密度较大、业务量较低、卫星相对运动角速度较高，因此极地地区的轨间链路将会暂时关闭，当卫星回到低纬度地区时再与相邻轨道建立轨间链路。

低轨道卫星通信系统基本模型可以表示为G(ν,ε,W(t)|υ∈ν,(u,υ) ∈ε)，其 中：一组节点由ν=u∪R∪G表示，包括用户卫星u，中继卫星R和地面节点G；ε=εisl∪εgsl是链路集合，εisl是ISL 集合，εgsl是星地链路（Ground-Satellite Link，GSL）集合；W(t)=(Wu,υ(t))表示在时间区间[t1,t2]上节点u与节点υ之间的代价函数，一般由可用带宽、传输时延、误码率等因素组成，[t1,t2]为卫星拓扑更新时间间隔。

2 路由算法

本文算法基于SDN 架构，路由计算由SDN 控制器实现，以节省星上有限存储计算资源。卫星通信网络中的每个节点在SDN 控制器中映射成虚拟节点，每个虚拟节点存储来自GEΟ 卫星报告的LEΟ 卫星节点链路状态信息，SDN 控制器将虚拟节点组成虚拟MPLS［22］网络，根据算法计算结果以标签的形式集成到ΟpenFlow［23］协议流表中，通过南向接口发送给LEΟ 卫星来执行数据转发任务。

2.1 初始权重函数

在虚拟MPLS 卫星网络中首先定义cu,υ为链接因子，当卫星节点u与节点υ之间无链路建立时cu,υ被置为0；当卫星节点u与节点υ之间有链路建立时cu,υ被置为1。定义Cm×m=(cu,υ)m×m为链接矩阵，代表卫星节点间的链路链接状况；Bm×m=(bu,υ)m×m为剩余带宽矩阵，代表链路的可获得带宽；Dm×m=(du,υ)m×m为传播时延矩阵，代表各星间链路的传播时延。

星间链路Su→Sυ的初始权重值定义如下：

其 中：Bu,υ(t)为链路Su→Sυ在t时刻的 剩余可用带宽；Bmax为当前卫星网络链路中可用剩余带宽的最大值；Du,υ(t)为链路Su→Sυ在t时刻的传播时延；Dmin为当前卫星网络链路中的最小传播时延；α、β为权重因子。

根据Cm×m，计算并获得从源卫星节点S到目的卫星节点D的标签交换路径集合：

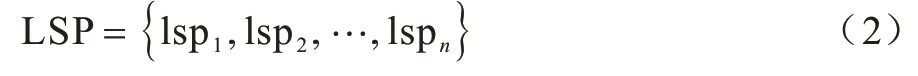
集合中共有n条可选用路径，lspk(1 ≤k≤n)代表第k条路径，则第k条路径的初始权重值定义如下：

其中：m表示lspk路径的总条数。

2.2 链路稳定度函数

考虑链路切换和QoS 保障的需要，定义3 种不同的业务服务类型ToS={tos1,tos2,tos3}，其中：tos1表示需要大带宽、低丢包率的业务，例如视频会议；tos2表示可容忍延迟但需要较大带宽的业务，例如大文件数据传输；tos3表示具有最高优先级的业务，即要求低时延、低丢包率和低抖动，例如信号指令数据传输。针对不同的业务类型，为了能够动态地分配和均衡网络流量负载，定义Tm×m=(tu,υ)m×m为链路稳定度矩阵，代表各星间链路在当前时间的链路剩余生存时间；Jm×m=(ju,υ)m×m为链路负载度矩阵，代表各卫星节点的负载程度。

在卫星星座系统中星间链路的通断在一个轨道周期内会发生多次切换，假设卫星Su与卫星Sυ在时刻建立星 间链路并在时刻链路断开，此时星间链路Su→Sυ的生存时间Tk定义如下：

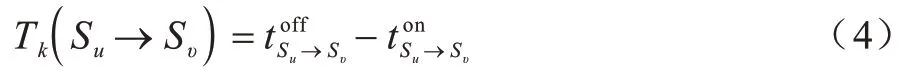
在任意时刻t，星间链路的剩余生存时间定义如下：

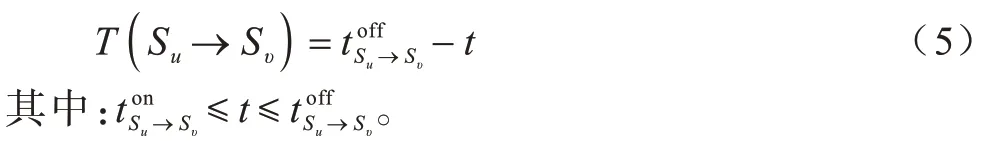
星间链路Su→Sυ的稳定度定义如下：

其中：Ttol为卫星星座系统的运动周期。

根据式（6）得到星间链路稳定度矩阵：

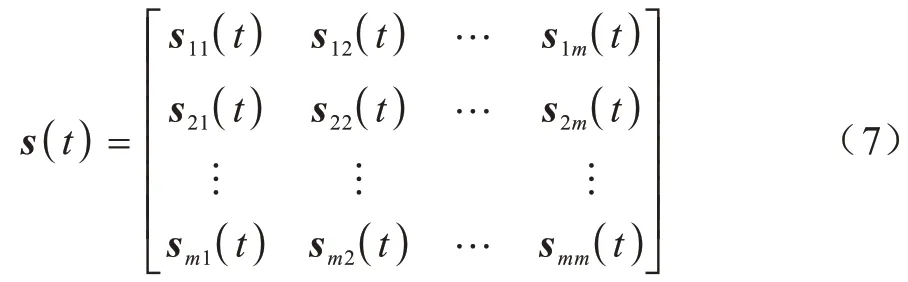
根据星间链路的剩余生存时间可以定义lspk(1 ≤k≤n)的星间链路稳定值：

其中：T(Su→Sυ)min为lspk(1 ≤k≤n)中各星间链路的最小链路剩余生存时间。

2.3 链路负载度函数

当有多个用户向SDN 控制器发起端到端的业务申请时，通过流量监测来获取网络的实时流量信息，动态分配整个卫星网络的业务流量，避免拥塞节点的出现。定义lspk(1 ≤k≤n)中每一条Su→Sυ的链路负载度为jk(t)，jk(t)计算公式如下：

其中：F(t)为t时刻星 间链路Su→Sυ被分配 的流量负载；P(t)为所有LSP 集合的总条数。

根据式（9）得到链路负载度矩阵：

定义lspk(1 ≤k≤n)的链路负载度函数：

其 中：Fmax(t) 为t时 刻lspk(1 ≤k≤n) 中星间链路Su→Sυ被分配的流量负载的最大值。

2.4 链路代价函数

通过考虑lspk(1 ≤k≤n)的初始权重函数、链路稳定度函数和链路负载度函数，定义权重因子矩阵：

其中：w11为tos1初始权重值的权重因子；w22为tos2链路稳定度的权重因子；w33为tos3链路负载度的权重因子。同时，有w11+w12+w13=1，w21+w22+w23=1 和w31+w32+w33=1。

将链路初始权重函数、链路稳定度函数和链路负载度函数归一化。根据式（3）得到归一化后的初始权重函数：

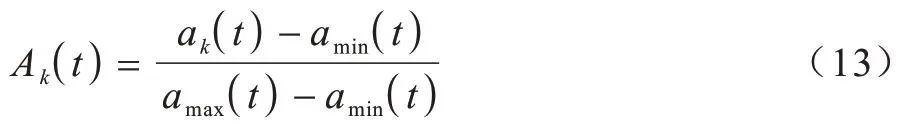
其中：amin(t)为lsp 中链路初始权重值的最小值；amax(t)为lsp 中链路初始权重值的最大值。

根据式（8）得到归一化后的链路稳定度函数：

其中：smin(t)为lsp 中链路稳定度的最小值；smax(t)为lsp 中链路稳定度的最大值。

根据式（11）得到归一化后的链路负载度函数：

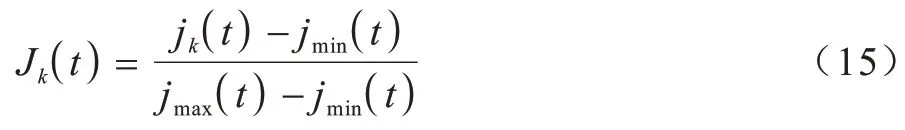
其中：jmin(t)为lsp 中链路负载度的最小值；jmax(t)为lsp 中链路负载度的最大值。

为减少瓶颈节点对链路初始权重函数的影响，引入调整因子Q并定义链路初始权重函数调整因子：

由此可以看出，当Ix(t)越大时的取值越大，从而可以减小瓶颈节点对链路初始权重函数的影响。

针对不同的业务服务类型tos1、tos2和tos3得出链路代价函数：

此时决策矩阵更新如下：

根据本文路由算法的决策矩阵，分配具有合适值的权重因子矩阵ω，从LSP 可选路径集合中为具有不同QoS 要求的业务类型选择合适的路由路径，完成路由转发。

本文算法主要由星间链路的状态信息交互与低轨道卫星的路由计算两部分组成，算法复杂度主要体现于路由计算过程。路由计算根据三大函数加权计算最优路径，可以看出本文算法的时间复杂度为常数级，传统SPFA 算法的时间复杂度为Ο（N2），其中N为卫星节点数。由于本文算法采用SDN 网络架构，低轨道卫星几乎只需存储状态信息，大幅节省了星上存储资源，占用的空间复杂度也为常数级，而传统SPFA 算法的空间复杂度为Ο（N），因此本文算法适用于卫星通信网络资源受限的应用场景。

3 仿真验证

为验证路由算法的有效性，利用STK 来构建低轨道卫星星座运动模型。卫星星座模型有4 个轨道平面，即NL=4，每个轨道平面由9 颗卫星组成，即ML=9，共有36 颗卫星。当卫星纬度超过75°时认为进入极区，轨间链路断开，仅保留2 条轨内链路。卫星星座参数如表1 所示。

表1 卫星星座参数Table 1 Satellite constellation parameters

通过STK 构建卫星星座模型，得到卫星的星间链路通断时间，卫星周期运动轨迹、位置距离等数据，构建低轨道卫星通信系统的网络拓扑模型。卫星星座模型如图2 所示。

图2 卫星星座模型Fig.2 Satellite constellation model

为验证本文路由算法的性能，仿真结果与SDRA［24］算法进行对比，并针对3 种不同需求的业务类型tos1、tos2、tos3，设置权重因子矩阵：

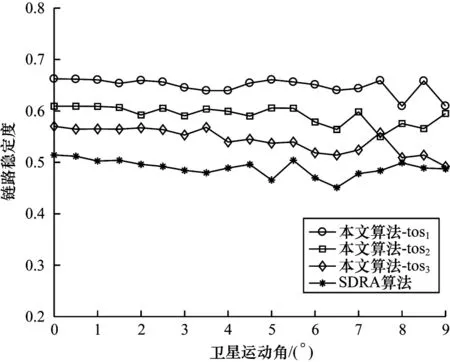
图3 链路稳定度对比Fig.3 Comparison of link stability degree

图4 给出了在相同的网络通信环境下业务类型tos1、tos2、tos3与SDRA 算法的链路负载度。由图4可以看出，本文算法的3 种业务类型对应的链路负载度均明显小于SDRA 算法，其中业务tos2的链路负载度权重因子最大，仿真结果表明其路径的平均链路负载度为最小，仅为0.37 左右。

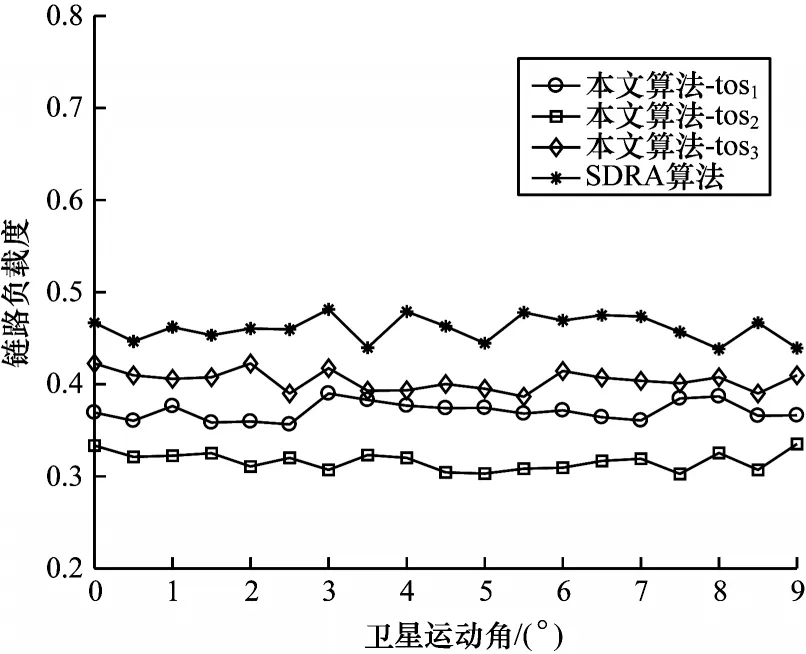
图4 链路负载度对比Fig.4 Comparison of link load degree

图5给出了在相同的网络通信环境下业务类型tos1、tos2、tos3与SDRA 算法的业务时延。由图5 可以看出，本文算法得出的3种业务类型的平均时延均低于SDRA算法，其中业务tos3对应时延的权重因子较大，平均时延均小于业务tos1和tos2的平均时延。

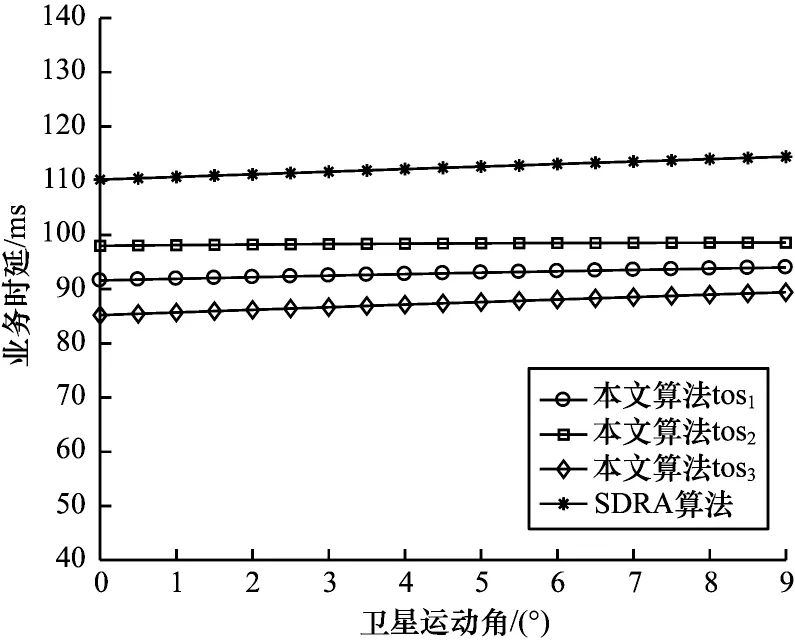
图5 业务时延对比Fig.5 Comparison of business delay

图6 给出了在不同数据发送速率下本文算法与SDRA 算法的吞吐量对比结果。由图6 可以看出，本文算法考虑链路状态、网络负载均衡等关键因素，得到的系统吞吐量明显高于SDRA 算法。综合仿真结果图3～图6 可以看出：本文算法在保证不同用户业务类型tos1、tos2、tos3的QoS 需求的前提下，在网络负载均衡、业务时延、系统吞吐量等方面均具有较明显的性能优势。

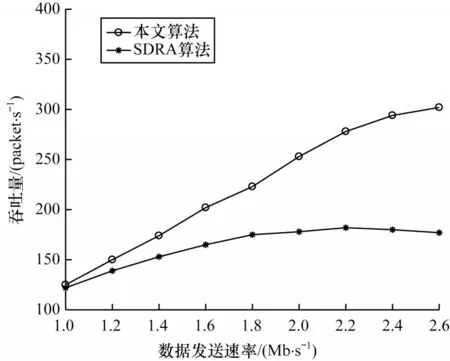
图6 不同数据发送速率下的吞吐量对比Fig.6 Comparison of throughput at different data transmission rates

4 结束语

本文提出一种支持QoS 的高性能LEΟ 卫星星间路由算法。利用SDN 网络架构节省有限的星上计算和存储资源，并提高卫星通信网络的自适应能力。考虑星间链路的时延、可用带宽、链路切换与负载等因素，定义星间链路的初始权重函数、链路稳定度与链路负载度。针对不同要求的业务服务类型，定义权重因子矩阵，并利用调整因子来减小瓶颈节点的影响，有效保证多用户的QoS 要求。仿真结果表明，本文算法相比SDRA 算法复杂度更低，不但在业务时延、系统吞吐量、网络负载均衡等方面具有良好的性能，而且保证了多用户的QoS 要求。下一步将对卫星通信网络中由业务服务类型数量众多导致的网络拥塞展开研究，进一步优化网络通信性能。