面向停电分类预测的因子分解机模型

冉 懿，王润年，潘红伟，俞海猛，袁培森

（1.国网新疆电力有限公司 营销服务中心，乌鲁木齐 830000；2.国电南瑞南京控制系统有限公司，南京 211106；3.南京农业大学 人工智能学院，南京 210095）

0 概述

可靠的电力供应对于现代社会的发展至关重要，社会生产中的很多方面都依赖于电力建设，因此，电力设施被认为是现代社会中较为关键的基础设施之一［1-2］。一旦停电，会严重影响人们的日常生活［3-4］以及其他关键基础设施系统的运行，从而造成巨大的经济损失。

为了更好地分析和管理电网系统所产生的电力数据，电网企业搭建了智慧电力大数据平台。通过对平台中的停电数据进行分析和挖掘，可以更好地了解电网停电的潜在规律［5-6］。通过分析历史停电数据，根据分析所得的规律进行停电分类预测，能够为依赖于电力设施的其他公司、公共事业单位等的停电规划安排提供决策参考［7］。从短期看，电网停电的分类预测可以帮助企事业单位提前做好准备，平衡人力、材料成本以及加快电力恢复速度；从长期看，可以根据停电数据分析得到电力系统中需要加强的板块，还能够通过数据分析来设置合适的备用电源数目，以提高本地电网系统的供电可靠性［8］。

目前，国内外学者针对电力停电分类预测问题进行了大量研究，并且取得了一定成果。XIE 等［9］通过分析雷电天气的停电数据，提出一种基于通用回归神经网络（GRNN）的方法，以预测雷电天气下的停电情况。该方法对历史雷电天气的停电数据进行特征提取，并将提取的特征作为GRNN 的输入以训练模型，然后根据训练的模型来预测停电情况。ZHAI 等［10］设计一种新模型，其通过使用公开可用的数据来准确估计各个建筑物级别的停电情况。该模型使用脆弱性函数模拟在危险负荷下单个建筑物级别的停电情况，能够提供更多的本地化、建筑物级别的估计，以评估由于自然灾害而造成的停电。侯慧等［11］采用随机森林方法，结合气象、地理数据来预测不同区域的停电情况，并通过对停电网格进行重要性评估来提高预测的准确性。

本文提出一种基于因子分解机（Factorization Machine，FM）的方法，以对停电数据进行分类预测。为了提取有效的特征来降低数据处理的复杂度，通过决策树算法对停电数据进行特征选择。为了获取更多的有效特征，基于不同地区的空间位置，利用矩阵分解构造空间位置特征。通过梯度下降方法训练因子分解机模型，为了防止模型过拟合，在优化目标中加入L2 正则化。在此基础上，利用所训练的模型进行停电数据分类预测，从而为电网公司的用电决策提供参考。

1 特征选择

在特征选择时，需要避免选择太多或太少的特征：如果选择的特征太少，则特征数据中蕴含的信息内容可能会很少；如果选择的特征太多，则可能会存在一些不相关的特征，从而提高任务学习的难度。本文通过决策树［12］进行特征选择，具体地，计算得到不同特征在决策树上所作的贡献，通过贡献度的大小来选择特征。同时，采用基尼系数（Gini）来衡量不同特征的重要性。Gini 最早用于经济学领域，主要用于衡量收入分配的公平性。在决策树的构建过程中，Gini 通常用来测量数据的纯度或不确定性。

假设样本数据有C个特征X1,X2,…,XC，特征Xj的基尼系数表示决策树中第j个特征节点分裂不纯度的平均变化量。Gini 的计算方式如式（1）所示：

其中：K表示类别总数；pk表示第k个类别所占的比例。

特征Xi的某个取值x将样本数据分成2 个部分D1、D2，则特征Xj的基尼系数的计算方式如式（2）所示：

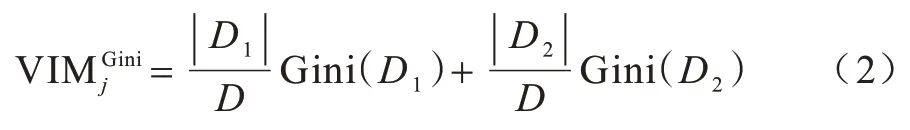
其中：Gini(D1)表示D1的Gini；Gini(D2)表示D2的Gini。

利用决策树算法计算部分特征的重要性分数，对计算出的不同特征的重要性分数进行排序，从中选择对停电分类预测较为重要的特征用于模型训练。

2 停电预测方法

2.1 特征构造

为了利用更多的有效特征，本文在已有停电数据的基础上，根据不同地区的地理位置关系构造新的位置关联特征。本文认为相邻地区之间的停电情况具有相关性，如果2 个区域相邻或有重叠的地理区域，则某地区停电，相邻的区域也有很大的可能性停电。

假设共有n个区域p1,p2,…,pn，现构造一个关联矩 阵An×n，如 果2 个区 域pi、pj相邻或有重叠的地理区域，那么对应的矩阵元素值aij为1，其他非对角线元素值均为0。由不同地区构造出来的关联矩阵An×n的形式如下：

其中：aii的值为1；aij表示地区pi和pj之间的停电关联值，2 个区域相邻或有重叠的地理区域，aij=1，否则aij=0。

显然，矩阵A的值不能直接作为停电特征，需要对A进行矩阵分解，本文采用LU 分解的方式来完成。LU 分解［13］是将矩阵变成下三角矩阵与上三角矩阵的乘积，其形式如下：

其中：L为下三角矩阵，即当i＞j时，lij=0；U为上三角矩阵，即当i＜j时，uij=0。

对于停电样本数据，每一行代表一个区域的停电情况，一共有n个区域p1,p2,…,pn。式（4）将矩阵A分解成n×n矩阵L与n×n矩阵U的乘积，假如样本数据的第i行是区域pi的停电情况，那么该行对应的空间位置构造特征就是矩阵L的第i行数据。通过矩阵分解的方式构造不同区域的空间位置特征，可以为模型训练提供更多的有效特征，从而提升模型的分类准确性。

2.2 因子分解机

FM 将支持向量机的优点与因子分解模型相结合［14］，其可与任何实值特征向量一起使用，是一种通用预测模型。FM 的机制是使用分解参数对变量之间的交互进行建模，即使在具有稀疏性的问题中也可以估计交互，对于停电数据中存在的大量稀疏特征，如月份、年份等，FM 具有适用性。此外，由于FM的模型方程可以在其因子数量k和特征数量n方面都降为线性复杂度，因此FM 的计算效率很高，这也意味着FM 模型的预测时间是线性的，且减少了训练阶段要学习的参数量［15-16］。

假设X∈Rn表示维度为n的特征向量表示2个大小为k∈的向量的点积，向量的点积计算如下：

FM 能够通过使用因子分解模型来对不同特征之间的交互进行建模，尤其是FM 模型通过分解交互特征以估计交互，从而打破交互特征之间的独立性。FM 模型考虑到不同特征之间的关联关系，引入交叉项，通过对特征两两相乘来找到一些组合特征。对于二阶交叉，FM 模型方程如下：

将式（7）中的结果代入式（6），得到预测值的表达式为：

通过数学变换，FM 计算方程的时间复杂度降为Ο(kn)，这也说明FM 模型的计算成本相对于潜在特征的维数和特征是线性的。

停电分类预测属于二分类问题，本文采用logitloss 函数作为FM 模型的损失函数，其表达式如下：

由式（9）可以看出，模型的预测值和真实值越接近，则损失函数的值越小。

FM 模型的目标是总损失函数最小化，总损失函数计算如下：

由于本文损失函数选择的是logitloss 函数，因此总损失函数被更新为：

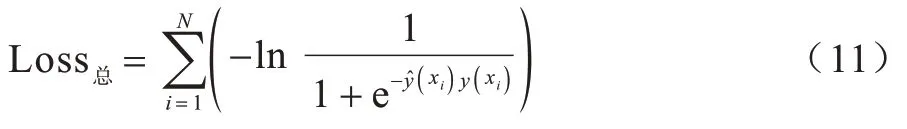
针对FM 模型的优化，目标如下：

为防止FM 模型过拟合，本文引入一种L2-范数正则化优化技术［17］，L2 范数正则化的基本思想是在原始成本函数中添加一个额外项，称为正则项，其中仅包含L2 范数误差项，并带有一个用于控制正则化相对量的超参数。可以将这种技术视为在原始L2范数误差项和L2 范数正则项之间的一种折衷方法，其能增强FM 模型的泛化能力。加入L2-范数正则项后的优化目标更新为：

其中：λ为L2 正则化的系数，λ的取值影响FM 模型的泛化能力。

本文通过随机梯度下降［18］的方法训练FM 模型。随机梯度下降是不断地沿着目标函数梯度的反方向去寻找损失函数值最小的参数。求损失函数y（x）关于θ的偏导，如下：

其中：σ(·)表示sigmoid 函数。

利用随机梯度下降的方法训练FM 模型的算法描述如算法1 所示。

算法1FM 模型训练算法

算法1 通过随机梯度下降算法训练FM 模型：首先，对FM 模型中的参数进行初始化操作；接着，利用随机梯度下降算法根据设置的学习率对FM 中的参数进行更新，每次更新后计算给定条件是否满足，如果满足，则停止迭代，如果不满足，则继续迭代更新直到满足更新条件；最后，返回停止迭代后的模型参数值。

3 实验分析

3.1 实验数据集与评估标准

本文采用的实验数据集一共包括23 768 条数据，记录了14 个地区的停电情况，数据包括天气、人口、停电时间等非稀疏特征，以及年份、月份、地区等稀疏特征。

本文采用基于混淆矩阵［19］的评估度量。混淆矩阵如表1 所示。

表1 混淆矩阵Table 1 Confusion matrix

TTP是真阳性，表示被分类器正确分类的正类数据；TTN是真阴性，表示被分类器正确分类的负类数据；FFP是假阳性，表示被分类器错误地标记成正类数据而实际是负类的样本数据；FFN是假阴性，表示被分类器错误地标记为负类而实际为正类的样本数据。根据混淆矩阵计算分类器的准确率（Accuracy）和F1 值（F1-score），以衡量模型的性能［20-21］。准确率和F1 值的计算公式如下：

其中：P表示精确率；R表示召回率。P和R的计算方式如下：

根据分类器混淆矩阵的值，即可计算最终的分类器分类准确率和F1 值。

3.2 结果分析

本文利用决策树算法计算城市停电数据非稀疏特征的重要性，根据计算出的不同特征的重要性和设定的阈值，筛选出对停电数据分类预测相对重要的特征以训练FM 模型，从而提高FM 模型的分类预测性能。通过决策树算法计算的非稀疏特征的重要性得分结果如图1 所示，将重要性分数的阈值设置为0.1，本文选取重要性分数排在前4 位的非稀疏特征进行模型训练。

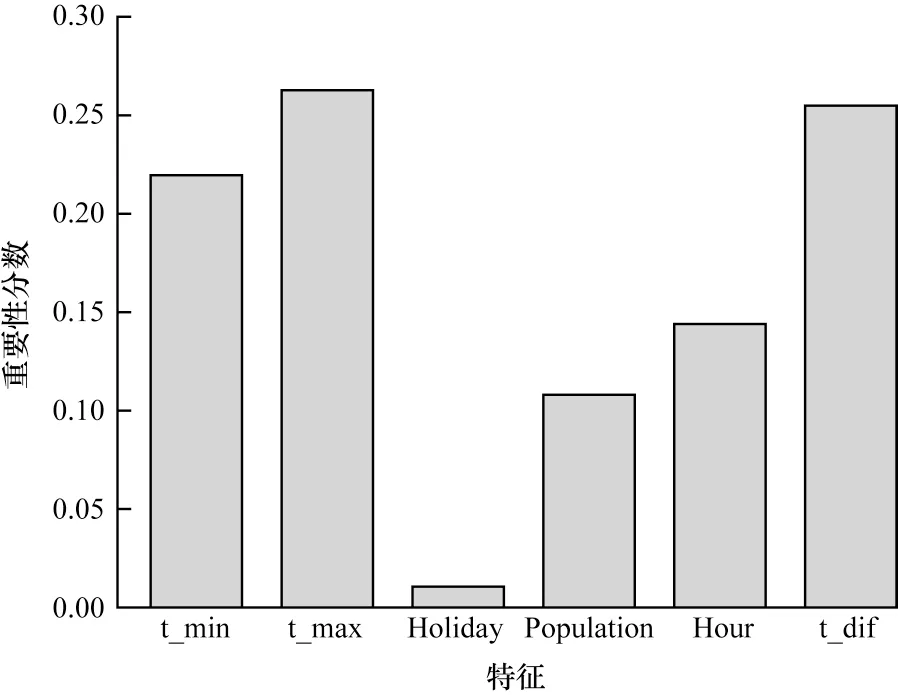
图1 非稀疏特征的重要性分数Fig.1 Importance score of non-sparse features

为了进一步说明特征提取的必要性以及根据决策树算法提取特征的有效性，本文分别利用上述选取的特征以及全部的非稀疏特征进行实验，比较2 种情况下的F1值、准确率以及运行时间，实验结果如表2所示。从表2 可以看出：本文特征提取方法能够有效提升FM模型的性能，在F1 和准确率2 项指标上均有提升；利用全部非稀疏特征训练模型的时间大于特征提取后的模型训练时间，这说明经过特征提取后再进行模型训练，能够节约训练时间，节省CPU 资源。

表2 特征提取前后的实验结果Table 2 Experimental results before and after feature extraction

本文利用筛选出的非稀疏特征和稀疏特征来训练FM 模型，训练次数设置为200 次。随着训练次数的增加，模型分类预测的准确率和F1 值如图2 所示。从图2 可以看出，随着模型的不断训练，准确率和F1值都在提高，这说明FM 模型的分类预测效果越来越好，且当迭代次数较多时，对于停电数据能够取得较好的预测效果。此外，当迭代次数达到一定数值时，指标值变化很小，基本趋于稳定，说明模型的分类性能保持稳定。

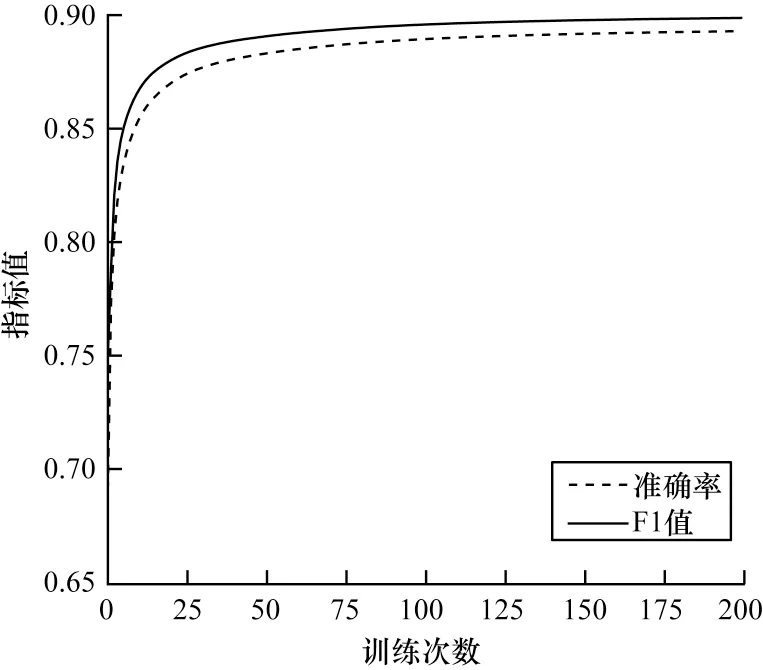
图2 模型的准确率和F1 值变化曲线Fig.2 The accuracy and F1 value curve of the model

本文将FM 模型和线性分类（Linear）模型、深度神经网络（DNN）模型、支持向量机（SVM）模型、朴素贝叶斯（Bayes）模型、XGBoost 模型［22］进行对比，比较不同模型的准确率和F1 值。对于不同的分类预测模型，训练数据集和测试数据集的比例均为3∶1。

训练数据集在不同模型下的准确率和F1 值结果如表3 所示。从表3 可以看出，FM 模型的分类效果均优于另外5 种模型。F1 值为分类模型召回率和精确率的综合指标，也是衡量模型分类预测性能的综合指标，其值越大，说明模型的分类预测效果越好。FM 模型在训练数据集下的F1 值为0.90，比线性分类模型提高11%，比DNN 模型提高34%，比SVM 模型提高17%，比朴素贝叶斯模型提高23%，比XGBoost 模型提高8.4%。准确率是表示模型将正负样例正确分类的能力，其值越大，说明模型分类正确的比例越大，模型性能越好。FM 模型在训练数据集下的准确率为0.89，比线性分类模型提高11%，比DNN 模型提高30%，比SVM 模型提高17%，比朴素贝叶斯模型提高22%，比XGBoost 模型提高8.4%。根据准确率和F1 值可以看出，训练数据集在FM 模型下效果较好，并且优于其他模型，这是因为在电力数据中存在大量的稀疏数据，而FM 针对稀疏性问题也可以估计交互，其借助因子分解技术打破了交叉项参数之间的独立性，使得在稀疏性问题中具有更强的学习能力。

表3 训练集中不同模型的评价指标结果Table 3 Evaluation index results of different models in the training set

测试数据集在不同模型下的准确率和F1 值结果如表4 所示。从表4 可以看出，FM 模型的分类性能评价指标均优于其他模型。FM 模型在测试集下的F1 值为0.90，F1 值越接近1，模型的分类预测效果越好。FM 模型的F1 值比线性分类模型提高12.5%，比DNN 模型提高43%，比SVM 模型提高18%，比朴素贝叶斯模型提高23%，比XGBoost 模型提高9.8%。测试集下FM 模型的准确率为0.89，说明有89%的样本数据被正确分类。FM 模型的准确率值比线性分类模型提高11.3%，比DNN 模型提高38.5%，比SVM模型提高18.4%，比朴素贝叶斯模型提高21.6%，比XGBoost 模型提高8.5%。无论是准确率还是F1 值，测试数据集在FM 模型下的结果都较好，利用训练集训练出来的模型，用测试集去验证其性能，得到的结果依旧较好，并且都优于另外5 种模型，这再次验证了使用FM 模型对停电数据集进行分类预测具有有效性。

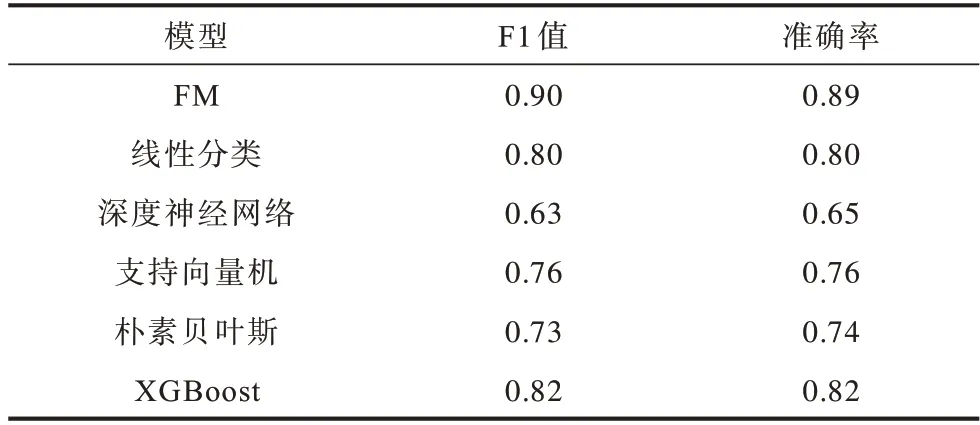
表4 测试集中不同模型的评价指标结果Table 4 Evaluation index results of different models in the test set

4 结束语

针对停电分类预测问题，本文提出一种基于随机梯度优化的FM 分类预测模型。利用决策树算法计算停电数据中不同特征的重要性得分，根据设定的阈值筛选出与停电预测关联度较大的特征。利用不同地区的空间位置建立位置矩阵，通过矩阵分解构造空间特征。基于选择的特征对应的样本数据使用随机梯度下降方法训练FM 模型，并加入L2 正则化以防止模型过拟合，最终利用训练好的FM 模型对停电数据进行分类预测。实验结果验证了FM 模型在停电数据分类预测任务中的有效性。下一步将对不同季节的停电数据进行分类，利用自编码器模型对停电数据完成特征提取并对多维数据作降维处理，使用降维后的数据特征训练FM 模型，从而提高模型的分类预测精度。