一种基于多步竞争网络的多智能体协作方法

厉子凡，王 浩，方宝富

（合肥工业大学计算机与信息学院，合肥 230601）

0 概述

多智能体协作是指多个智能体之间相互合作完成一项任务或者分别完成复杂任务的某项子任务。目前，基于深度强化学习（Deep Reinforcement Learning，DRL）［1］的多智能体协作成为研究热点，已在多智能体协同控制［2］、交通控制［3］、资源调度［4］、自动驾驶［5-6］、游戏AI［7］等领域得到广泛应用。将DRL与多智能体系统（Multi-Agent System，MAS）相结合，称为多智能体深度强化学习（Multi-Agent Deep Reinforcement Learning，MADRL）［8］。

多智能体决策系统中主要存在环境非平稳、智能体数量增加导致的维数灾难和多智能体信用分配等问题，这些问题对MADRL 而言是巨大的挑战。分散式方法［9-11］令每个智能体只学习自己的个体动作值函数，并将其他智能体看作是环境的一部分，然后直接应用单智能体深度强化学习（Single-Agent Deep Reinforcement Learning，SADRL）算法学习策略。这样可以避免维数灾难，但由于其他智能体的策略在不断变化，智能体学习到的策略也会随之不断变化，从而出现非平稳特性。集中式方法［12-14］考虑所有智能体信息直接学习联合动作值函数，可以减轻非平稳性带来的不利影响，但随着智能体数量的增加，参数空间会呈指数级增长，联合动作值函数将难以有效学习并用于智能体数量较多的环境，导致拓展性较差。

近些年来，结合了分散式方法和集中式方法各自优势的值分解方法［15-17］成为主流方法。值分解方法先分散地学习每个智能体的个体动作值函数，然后集中利用个体动作值拟合联合动作值函数。在此方法框架下，联合动作值函数的计算复杂度随智能体数量呈线性增长，同时也考虑了所有智能体的信息，在环境平稳性和智能体拓展性之间取得了较好的平衡。然而，现有的一些值分解方法忽视了智能体策略网络的重要性，而将研究的重点集中到了联合动作值函数的学习上。此外，在学习联合动作值函数时也没有充分利用经验池中保存的完整历史轨迹，仍然以单智能体常用的单步更新方式学习。

本文提出基于多智能体多步竞争网络（Multiagent Multi-step Dueling Network，MMDN）的多智能体协作方法，借鉴值分解思想，在集中式训练分散式执行（Centralized Training with Decentralized Execution，CTDE）［18］框架的基础上，将动作评估与状态估计解耦，利用整条历史轨迹估计时间差分目标，以集中式端到端的方式训练智能体分散策略。

1 相关工作

基于MADRL 的多智能体协作方法大致可以分为分散式方法、集中式方法、值分解方法3 类。

分散式方法直接应用SADRL 算法建模智能体，每个智能体仅学习个体动作值函数，将其他智能体看作是环境的一部分。2017 年，TAMPUU 等［9］将深度Q 网络（Deep Q Network，DQN）［19］应用到多智能体环境。同年，GUPTA 等［11］进一步将异步优势行动者-评论家（Asynchronous Advantage Actor-Critic，A3C）算 法［20］、深度确 定性策 略梯度（Deep Deterministic Policy Gradient，DDPG）算 法［21］、置 信域策略优化（Trust Region Policy Οptimization，TRPΟ）算法［22］应用到多智能体环境。由于无法解决非平稳性的问题，分散式方法在复杂协作场景中往往无法发挥作用。

集中式方法中每个智能体均利用所有智能体的信息学习联合动作值函数，这样可以减轻非平稳性带来的不利影响，但是存在拓展性的问题，难以用于智能体数量较多的环境。反事实多智能体（Counterfactual Multi-Agent，CΟMA）策略梯度算法［13］是基于行动者-评论家（Actor-Critic，AC）框架的算法，所有智能体的Actor 网络与一个中心化Critic 网络连接。中心化Critic 网络使用特殊的反事实模块输出联合优势函数值。由于只有一个中心化的Critic，因此CΟMA 在异构智能体场景中往往无效。多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient，MADDPG）算 法［12］在DDPG 的基础上为每个智能体建立一个中心化的Critic，在训练阶段使用所有智能体的信息而非个体信息以缓解非平稳性，并为每个智能体保留多个子策略。MADDPG 不能直接应用于具有离散动作空间的环境。

值分解方法兼具分散式方法和集中式方法的优势，可在环境平稳性和智能体拓展性之间取得平衡。但是值分解方法基于一定的限制条件，多用于完全协作的多智能体任务。值分解网络（Value-Decomposition Network，VDN）算法［15］将联合动作值函数分解为每个智能体个体动作值函数的简单和，从而将一个复杂的学习问题分解为多个局部的更易学习的子问题。单调值函数分解（QMIX）算法［16］引入超网络［23］来学习联合动作值函数与个体动作值函数之间的非线性关系，并限制联合动作值函数和个体动作值函数满足单调约束。值函数变换分解算法（QTRAN）［17］直接学习联合动作值函数，并构造了多个损失函数用于优化，但该方式难以求解优化问题，并且在复杂任务中很难取得较好的效果。

2 基于MMDN 的多智能体协作

2.1 去中心化部分可观察马尔科夫决策过程

完全合作的多智能体任务可以被描述为去中心化部分可观察马尔科夫决策过程（Decentralized Partially Οbservable Markov Decision Process，Dec-PΟMDP）［24］。Dec-PΟMDP 可以定义为一个九元组G=＜N,S,U,P,r,Ο,Z,n,γ＞，其 中，N={1,2,…,n}表 示有限数量智能体集合，S表示环境状态集合，s∈S表示环境真实状态，U表示联合动作空间，Ο表示联合观察集合，Z表示观察概率函数，γ∈[0,1]表示折扣因子。在每一个时间步内，每个智能体i∈N={1,2,…,n}选择一个动作ui∈Ui组成联合动作u∈U，环境通过状态转移方程P(s′|s,u)：S×U×S→[0,1]得到下一步状态s′，r(s,u)：S×U→R 表示奖励函数。

在一个部分可观察的环境中，每个智能体仅能根据观察函数Z(s,u)：S×U→Ο得到自己的观察信息οi∈Ο。每个智能体有自己的动作-观察历史τi∈T≡(Ο×Ui)*，并以此 遵循随 机策略πi(ui|τi)：T×U→[0,1]。联合策略π拥有一个联合动作值函数：τ∈TN表示一个联合动作观察历史。

2.2 个体全局最大条件

值分解的核心是将联合动作值函数Qtot看作是由每个智能体的个体动作值函数Qi线性或非线性组合而成的（如式（1）所示），直接对联合动作值函数进行优化，通过梯度传播端到端地更新个体动作值函数。

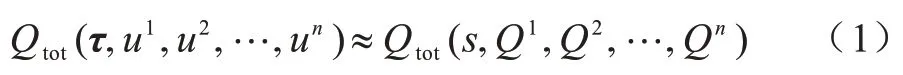
在值分解框架下，通常将个体全局最大（Individual Global Max，IGM）［17］作为智能体执行分散策略的条件。该条件确保了对联合动作值函数和个体动作值函数的动作选择保持一致，遵循CTDE框架。

定义1对于一个联合动作值函数Qtot(τ,u)：TN×U→R，如果存在个体动作值函数[Qi(τi,ui)：T×Ui→满足式（2），那么在τ下[Qi]对Qtot满 足IGM 条件［17］。在这种情况下，Qtot(τ,u)可以分 解为[Qi(τi,ui)]。

2.3 多智能体多步竞争网络

在强化学习中，时间差分学习直接从历史经验中学习而无需学习环境的完整知识，可以基于其他状态的估计值来更新当前状态的价值函数，更新规则如下：

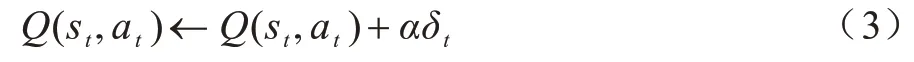
其中：α∈（0.1］表示学习步长；t表示时间步；δt表示t时刻的时间差分误差。

智能体决策具有一定的连续性，若要估计当前决策对所有未来决策的影响，需要对较长的决策序列进行整体考虑，即从经验池中取出整条轨迹时，可以利用当前时间步及之后n步的数据进行学习。动作值函数可以用来评估当前的决策对未来的效益，联合动作值函数Qtot由个体动作值函数Qi构建，对Qtot进行更新可以端到端地训练Qi。基于Q 学习的n步回报［25］可表示如下：

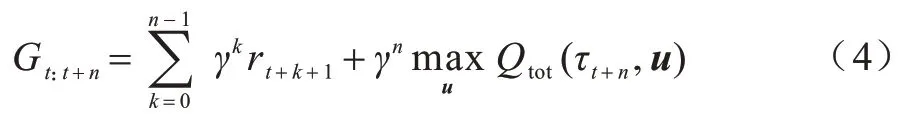
值得注意的是，n步学习可以减少更新目标时的偏差，但会引入高方差［26］。

为了缓解这一问题，本文引入λ-回报［27］作为时间差分目标的估计。λ-回报可以平均不同n的n步回报，同时通过调节参数λ可以权衡方差和偏差［28］。λ-回报定义如下：

其中：λ∈[0,1]是调节平均程度的参数。当λ=1 时，退化到蒙特卡洛方法；当λ=0 时，退化到一步时间差分方法。换言之，λ越大，考虑的轨迹越长；λ越小，考虑的轨迹越短。式（6）的等价写法更能体现这一性质。

将λ-回报代入时间差分学习的更新规则后，可以推导出如式（7）所示的联合动作值函数更新规则：

为了实现上述更新过程，本文设计如图1 所示的MMDN 结构，其由3 个部分组成：1）估计优势函数的智能体网络；2）估计状态值函数的价值网络；3）估计联合动作值函数的混合网络。

图1 MMDN 结构Fig.1 Structure of MMDN

其中：Q(τ,u)表示动作值函数；V(τ)表示状态值函数。优势函数用于衡量动作的优劣，因为在同一状态下状态值V(τ)是一个固定的值，所以在优势函数和动作值函数上根据贪婪策略选取最优动作是等价的，即智能体网络结构如图2 所示，由2 个多层感知机（Multilayer Perceptron，MLP）和1 个门控 循环单 元（Gated Recurrent Unit，GRU）组成，激活函数为ReLU，其中表示智能体i在t时刻由GRU 产生的隐藏状态。

图2 智能体网络结构Fig.2 Structure of agent network

价值网络用于估计全局状态的优劣，将全局状态st作为网络输入，将全局状态值V(τt)作为输出。MMDN 使用智能体网络和价值网络共同估计动作值函数，因此式（8）存在不可辨识的问题［29］，即当V和A加减同一个常数时，Q是不变的，但V和A却可能发生很大的变化。为缓解这一问题，本文在实施过程中采用式（9）计算动作值：

其中：α是价值网络的权重参数；β是智能体网络的权重参数；Qi(τi,ui；α,β)表示智能体个体动作值函数的参数化估计；|U|表示动作空间大小。将使用全局信息估计的全局状态值函数V(τ；α)代替使用每个智能体观察估计的局部状态值函数Vi(τi；α)，这样做可使Qi(τi,ui；α,β)在训练过程中聚合全局信息，帮助智能体更快更好地学习策略。在测试过程中，价值网络不参与决策，以满足集中式训练分散式执行框架。价值网络结构如图3 所示，其由3 个MLP 组成，激活函数为ReLU。

图3 价值网络结构Fig.3 Structure of value network

混合网络用于拟合联合动作值函数，将每个智能体的个体动作值作为输入，将联合动作值作为输出。本文同样利用超网络训练混合网络的权重参数。混合网络结构如图4 所示。超网络是学习神经网络权重参数的神经网络，w1和w2即超网络利用全局状态s学习的权重，w1和w2之间的激活函数为ELU，两个MLP 之间的激活函数为ReLU。个体动作值经由两层权重层非线性计算得到联合动作值。

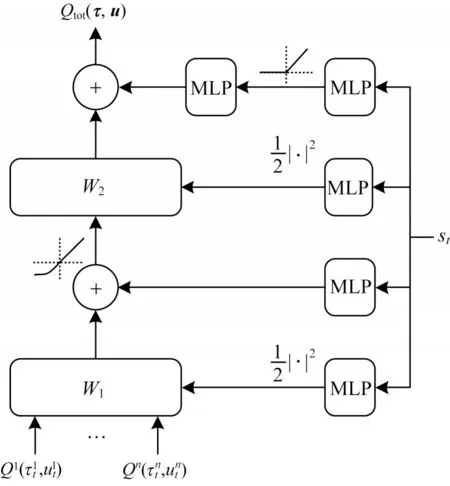
图4 混合网络结构Fig.4 Structure of mixing network

为了有足够多的训练数据，本文设置一个额外的经验池存储一个情节中所有智能体的历史轨迹。一个情节指从任务开始到任务结束或达到终止条件的整个过程，因此每个情节中的轨迹都是连续的，以方便GRU 的训练。

MMDN 通过最小化如式（10）所示的损失函数端到端地更新所有模块的网络权重参数：

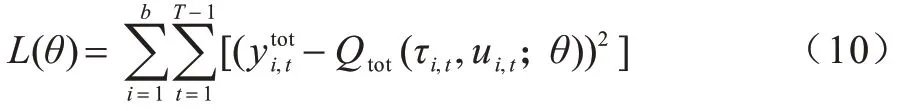
算法1MMDN 训练算法

3 实验与结果分析

3.1 实验设置

选择聚焦多智能体微观管理的对抗场景的SMAC［30］作为基准测试环境，所有方法需要对每个智能体进行细粒度控制，以评估单个智能体能否学会同其他智能体协作完成对战任务。

基于MMDN 的多智能体协作方法与基于CΟMA［13］、VDN［15］、QMIX［16］、QTRAN-base［17］、QTRAN-alt［17］的多智能体协作基线方法在8m、2s3z、2s_vs_1sc、MMM、3s5z、1c3s5z 等6 个场景中进行性能评估。所有方法均与内建的启发式游戏AI 进行对抗并计算胜率，内建的AI 的难度等级设置为非常困难。实验环境的详细信息和算法复现可以参考文献［30］。

在所有场景的训练过程中，每个智能体分散地使用-贪婪策略选择执行动作。随着训练过程的进行，在50 000 个时间步中从1.0 线性衰减到0.05，并在以后的训练过程保持不变。折扣因子λ设置为0.99。优化器选用RMSprop，学习率设置为0.000 5。当一方获胜或达到最大时间步后，一个情节终止。所有场景中的最大情节数为20 000，经验池包含最近的4 000 条完整历史轨迹。每次更新过程从经验池中均匀地采样32 个批量样本，并在完整的历史轨迹上训练。每次训练完100 个情节后暂停训练并独立地运行20 个情节进行评估，每个智能体分散地使用贪婪策略选择目标动作。测试胜率指算法控制的智能体在一定时间内击败所有敌方单位的情节数占总测试情节数的百分比。目标网络的权重参数为每200 个情节更新一次。

3.2 实验结果与消融研究

图5 给出了6 种方法在6 个场景中的评估结果。在每个场景中每种方法按照不同的随机种子运行5 次，取5 次结果的均值。从图5 的实验结果可以看出：

图5 在6 种不同场景中的胜率结果Fig.5 Results of win rates in six different scenarios

1）CΟMA 的表现相对而言劣于其他基于值函数的方法，在异构环境中均为最差。这也许与其仅有一个中心化Critic 不能很好地处理异构智能体信息有关。

2）QTRAN-alt 综合而言是基于值函数的方法中性能表现最差的，明显劣于其他方法，在3s5z 和1c3s5z 两个复杂场景中完全无效。

3）QTRAN-base 相比QTRAN-alt 表现较好，但在两个复杂场景中也是几乎失效的，原因在于QTRAN相比于VDN 和QMIX 额外增加了两个损失函数以确保联合动作值函数和个体动作值函数满足文献［17］中定理1 或定理2 的条件，这样做使得优化问题的复杂度也增加到Ο(|S|·|U|n)，其中，|S|表示状态空间数量，|U|表示动作空间数量。相比之下VDN 和QMIX 的优化 复杂度 从Ο(|U|n)降低到Ο(n|U|)［31］。SMAC 尽管是一个离散动作空间的环境，但是其状态空间是非常大的，这就造成了QTRAN 的优化复杂度远高于其他方法，可能出现在计算上难以解决该优化问题，而且场景越复杂，算法性能表现越差。

4）QMIX 和VDN 的表现接近，在比较复杂的场景中QMIX 表现更好，在比较简单的场景中VDN表现更好。笔者认为这是由线性分解和非线性分解的表征能力导致的差异。在复杂场景中，线性分解表征能力受限，不足以很好地学习联合动作值函数，而在简单场景中，线性分解和非线性分解的表征能力没有较大区别，但是非线性分解使用神经网络需要额外的训练，线性分解只需直接进行计算。

5）MMDN 相比于基线方法，获得了最好的性能表现，尤其是在复杂的场景中性能提升非常明显。

对MMDN 进行进一步的消融研究，在场景2s_vs_1sc 和3s5z 中验证每个模块的有效性。

消融实验1探究将动作评估与状态估计解耦的有效性。MMDN 取消多智能体竞争网络结构后可被视 为引入λ-回报的QMIX，记 作QMIX（λ）。VDN+DN 可以视为使用线性混合网络且λ=0 的MMDN。图6 结果表明，采用多智能体竞争网络后方法的性能均得到了提升，这说明将动作评估与状态估计解耦有利于智能体做出更好的决策，提升方法的性能表现。

图6 消融实验1 的结果Fig.6 Results of ablation experiment 1

消融实验2探究不同的λ值对MMDN 性能的影响。分别选取λ等于0、0.4、0.8 和0.99 进行测试。图7 的结果表明，不同的λ值会对算法产生不同的影响。λ具有平衡偏差和方差的作用，若λ值取得太大，则多步估计的权重较高，不能缓解高方差；若λ值取得太小，则多步估计的权重较低，具有较大偏差。因此，在本文中选取λ=0.8。

图7 消融实验2 的结果Fig.7 Results of ablation experiment 2

消融实验3探究V和A的不可辨识问题。图8的结果表明，采用式（9）近似动作值函数比直接采用式（8）效果更好，场景越复杂性能差异越明显，说明式（9）确实可以缓解因不可辨识导致的训练不稳定问题。

图8 消融实验3 的结果Fig.8 Results of ablation experiment 3

4 结束语

本文提出一个基于MMDN 的多智能体协作方法，融合多智能体竞争网络结构、值分解思想和多步时间差分学习，将动作评估与状态估计解耦，充分利用整条历史轨迹学习联合动作值函数，权衡估计偏差与多步采样带来的方差，并且在环境平稳性和智能体拓展性之间取得较好的平衡，有利于训练与学习多智能体协作策略。实验结果验证了该方法的有效性。下一步将对多智能体竞争网络结构做进一步改进并拓展到连续动作空间，同时引入协作图、智能体通信等机制，提升其在更为复杂的多智能体协作任务中的性能表现。