景区人行悬索桥受力特征研究

周诗云， 李国平， 骆梦

(1.中交第二航务工程勘察设计院有限公司， 湖北 武汉 430061； 2.同济大学 土木工程学院， 上海市 200082；3.武汉机电工程学校， 湖北 武汉 430014)

由于悬索桥在景观上和经济上的独特优势，随着中国旅游业的不断发展，越来越多的景区在深山峡谷及河沟上选择架设人行悬索桥。但至今为止中国还没有正式的人行悬索桥设计规范，其设计计算缺乏相关理论依据，过去大部分人行悬索桥仅仅根据经验架设[1]。而目前关于人行悬索桥的设计理论仍不够成熟，其设计方法主要借鉴公路大跨径悬索桥的设计思路，考虑人群荷载工况作为最不利工况下结构的受力性能[2]。然而，由于人行悬索桥的功能与建造时经济性的要求，结构本身较普通公路大跨悬索桥而言，加劲梁刚度更低，结构更加轻柔[3]，在动力荷载的作用下会产生较大的振动和变形，为保证结构的安全，关于人行悬索桥振动的研究显得十分必要。现有的研究大多着眼于结构的侧向振动，探讨结构在风荷载作用下的振动过程[4-6]，并提出通过一些构造上的措施，如增设风缆、提高结构阻尼等方式来提高结构侧向刚度，改善其受力性能。而针对景区人行悬索桥特殊的荷载工况的研究少有涉及，事实上，景区人行悬索桥普遍刚度较低，且荷载工况复杂，除了普通的人群荷载外，还应考虑游客嬉戏打闹时产生的跑步、跳跃等特殊动力荷载的作用，其受力特征与大跨度悬索桥并不完全一致，单纯考虑人群均布荷载的结构设计方法存在一定的安全隐患。该文以湖南省张家界市景区某人行悬索桥为工程背景，通过建立空间有限元模型，分析行人跑步、跳跃等特殊工况作用下结构的受力特征，并与相同跨径和结构参数的双链悬索桥进行对比分析，提出改善景区人行悬索桥受力性能的建议。

1 计算模型

张家界市某景区内人行悬索桥，为单跨84 m的单链柔式钢索悬索桥。桥宽1.8 m，主缆矢跨比f/L=1/9，吊杆间距3 m，钢筋混凝土索塔高11.63 m，加劲梁采用纵横交错的纵梁与横梁构成；主缆采用7φ24 mm镀锌钢丝绳，吊杆采用Q235φ40 mm圆钢制成，加筋横梁采用I20b工字钢，纵梁为I14工字钢，桥面板为5 mm厚防滑钢板。由于人行悬索桥属于柔性悬挂结构，为解决小应变情况下的非线性大位移问题，应按几何非线性处理[7]。利用通用有限元软件建立全桥模型，并对结构进行初始平衡状态分析，通过调整使得结构在成桥时处于初始平衡状态。

2 景区人行悬索桥荷载工况

不同于公路桥梁，景区人行悬索桥主要承受活载为人行荷载，其特点是人流量较大，且游客嬉戏打闹，实际荷载工况较为复杂。单纯人群静载并不符合结构真实的受力状态。该文将从均布荷载、跑步荷载以及跳跃荷载3种工况出发，对比分析景区人行悬索桥的受力特征。

2.1 人群荷载工况

由于中国并没有正式的人行悬索桥规范，故而参考日本的小跨径悬索桥设计规范[8]中关于人行活荷载的规定，取较为极端的情况，其值为200 kg/m2。根据AISC规范，人的体重G服从N(700，145)的正态分布，取均值700 N，人群荷载全跨满布时约相当于423人站在桥上。人行悬索桥属柔性结构，其受力特征不仅受荷载大小的影响，更与荷载的作用形式与作用位置密切相关。该文主要考虑两种特殊人群工况下结构的受力：

(1) 人行荷载工况Ⅰ：全跨均布荷载，对应于对称荷载作用时的最不利情况。

(2) 人行荷载工况Ⅱ：半跨均布荷载，对应于非对称荷载作用时的最不利情况。

2.2 行人跑步荷载工况

研究发现，行人正常行走跑步时产生的力具有周期性，可以采用傅里叶级数的形式表示[9]：

(1)

式中：G为单人体重；fs为荷载频率；αi为第i阶荷载的动载因子；φi为第i阶荷载的相位角。

参考申选召[10]对人致振动的相关研究[10]对行人跑步荷载取值的相关建议，式(1)中相关参数取值为：α1=1.25，α2=0.3，α3=0.1，α4=0.08，α5=0.07，α6=0.06；φ1=-π/6，φ2=-5π/6，φ3=-π/2，φ4=-π/6，φ5=-5π/6，φ6=-π/2，荷载频率取4 Hz。采用定点激励的方式模拟行人的跑步过程：将相应跑步荷载直接加载在结构的固定点上，该点通常选在结构第1阶竖向振型振幅最大位置，对应该桥1/4跨径处。

另外，考虑到单人的跑步荷载对整个桥梁结构影响较小，同时单人荷载与景区游客大多成群出现的实际并不相符，该文考虑15个人跑步时对结构产生的效应(相当于计算最大人数的3.5%)。采用等效人群数Np的概念，将n个人在结构上自由跑动的最大加速度转化为Np个完全同步的行人跑步的最大加速度计算问题[11]。其计算式如下：

(2)

式中：n为人群总人数；ξ为振型阻尼比；ρ人为人群密度。

2.3 行人跳跃荷载工况

跳跃荷载是在景区人行桥上常见的荷载类型，是典型的非连续接触型人致激励，会对结构造成很大的动力作用。根据陈隽等提出的荷载模型[11]，式(1)中相关参数取值：α1=1.48，α2=0.594，α3=0.146，α4=0.059，α5=0.03，α6=0.015；φ1=1.59，φ2=1.6，φ3=1.58，φ4=1.54，φ5=1.58，φ6=1.55，荷载频率取3 Hz。

3 荷载工况分析结果

3.1 动力特性分析

考虑到时程分析的需要，先对悬索桥进行动力特性分析。将结构的自重、二期恒载等转化为各个方向的集中质量，采用特征值向量法，振型数量取300，保证各个方向上的振型质量参与系数均达到90%以上。悬索桥前10阶自振特性见表1，前4阶振型见图1。

表1 人行悬索桥自振特性

图1 人行悬索桥前4阶振型

结构的1阶振型为正对称侧向弯曲，2阶振型为反对称竖向弯曲，3、4阶振型则为反对称扭转。由表1可以看出：该桥的1阶振型频率约为0.270 5 Hz，而其余各阶频率相较于一般悬索桥而言也普遍偏低，这是由于人行悬索桥加劲梁刚度较低，使得整个结构更偏柔性，自振周期更长，动力稳定性也相对较差。

3.2 人群荷载分析

通过对结构在两种人群均布荷载工况下的分析可知：工况Ⅱ较工况Ⅰ更为不利，在全跨均布荷载作用下加劲梁最大应力约为29 MPa，由于约束方式的原因，端部应力更大，跨中位置挠度最大，约为0.12 m；而在半跨均布荷载作用下，加劲梁应力分布相对更为均匀，最大应力约为117 MPa，四分点位置挠度最大，达到0.55 m。

3.3 人行荷载分析

人行悬索桥在4 Hz行人跑步荷载作用下，结构的最大变形及加速度响应见图2、3。

图2 跑步荷载下结构变形响应

图3 跑步荷载下结构加速度响应

由图2、3可以看出：

(1) 就普通跑步荷载工况而言，荷载作用初期结构变形最大，峰值达到0.21 m，约为最不利人群荷载工况下结构最大变形的38%，其后，随着荷载的作用结构变形减小并趋于周期性变化，其值为(-0.11±0.02) m。荷载作用结束后结构变形缓慢减小，并在平衡位置附近做往复运动，逐渐恢复静止。

(2) 相比结构变形，其加速度响应较为平稳，随荷载的作用加速度迅速增大，随后变化逐渐趋于稳定，其值为(1.15±11.50) m/s2，并在荷载结束后急剧减小。

(3) 结构加劲梁最大应力为90 MPa，约为最不利人群荷载工况下的76%。

模拟15人在四分点附近同时跳跃时人行悬索桥的受力情况，结构的最大变形及加速度响应见图4、5。

图4 跳跃荷载下结构变形响应

图5 跳跃荷载下结构加速度响应

由图4、5可以看出：

(1) 在普通跳跃荷载作用下，结构变形迅速增至最大值，峰值约为0.42 m，相当于最不利人群荷载工况下结构最大变形的77%。随后结构变形在(-0.23±0.12) m范围内变化，直至荷载结束后逐渐减小。

(2) 相比变形响应，结构加速度响应曲线频率更高，接近荷载曲线频率，较跑步荷载下结构加速度响应波动更大，其最大振幅约为20.50 m/s2，并在荷载作用结束后迅速减小。

(3) 结构加劲梁最大应力为146 MPa，约为最不利人群荷载工况下的1.25倍。

3.4 特殊工况下的人行荷载分析

为了充分探究结构的力学性能，除了针对普通人行荷载外，接下来将对两种特殊工况下结构的受力特征进行分析。

3.4.1 横向非对称人行荷载

通过结构的动力特性分析，可知该桥的3、4阶振型皆为反对称扭转，其抗扭刚度较低，在横向不对称动力荷载作用下结构稳定性较差，而景区游客在游玩打闹时，也更倾向于集中在栏杆附近，使得实际的人行荷载合力作用点位置往往并不在截面中心，从而产生较大的扭转效应[12]。为探究最不利情况下结构的受力特征，模拟在桥梁横向半宽范围内进行人行荷载布载时的情况。在横向不对称荷载作用下结构的变形及加速度响应曲线变化规律同普通人行荷载类似，限于篇幅，仅列出15人在四分点附近横向半宽范围内同时跳跃时人行悬索桥的最大变形及加速度响应，结果见图6、7。

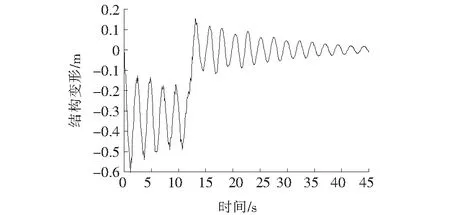
图6 非对称跳跃荷载下结构变形响应

图7 非对称跳跃荷载下结构加速度响应

由图6、7可以看出：

(1) 在横向不对称人行荷载作用下，结构最大的变形大幅增加，其中，非对称跑步荷载下为0.31 m，横向最大坡度达到10.2%；非对称跳跃荷载下为0.61 m，横向最大坡度达到21.6%。

(2) 在非对称跑步荷载工况下结构的最大加速度为17.81 m/s2，而在非对称跳跃荷载工况下结构加速度响应曲线波动较大，除极少数时刻加速度超过30 m/s2外(最大值52.76 m/s2)，其峰值振幅约为24.69 m/s2，均大于普通人行荷载下结构的最大加速度。

(3) 在非对称跑步荷载作用下加劲梁的最大应力为121 MPa，而在非对称跳跃荷载作用下则为190 MPa，相比普通人行荷载下的最大应力亦有所增加。

3.4.2 结构共振

考虑到景区人行悬索桥的特殊情况，游客游玩时常常故意奔跑晃动桥梁，使得桥梁产生较大的振动，所以实际桥上行人跑步的频率并不一定与常人跑步的频率一致。另取最极端情况：即跑步荷载频率与结构第1阶竖向振型的振动频率一致，以探究跑步荷载作用下桥梁共振时，结构的受力情况。发生共振时，结构的最大变形及加速度响应如图8、9所示。

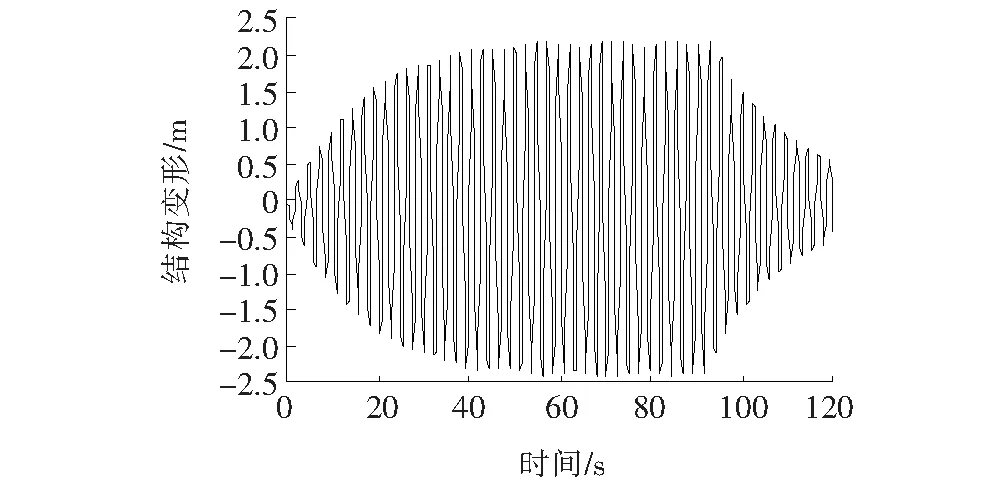
图8 跑步荷载下结构共振变形响应

图9 跑步荷载下结构共振加速度响应

事实上，相对于跑步而言，跳跃荷载的频率更难于人为控制，其变化范围更小，结构发生共振的概率较低，但为探究极端情况下景区人行悬索桥的力学特性，该文取结构第1阶竖向振型的振动频率作为行人跳跃频率，分析共振时结构的受力情况。其最大变形及加速度响应如图10、11所示。

图10 跳跃荷载下结构变形响应

图11 跳跃荷载下结构加速度响应

由图8～11可以看出：

(1) 人行悬索桥发生共振时变形大幅增加。随着荷载的作用结构动能不断累积，变形逐渐增至最大值，之后不再减小，并保持最大振幅做周期性振动，在跑步共振时其振幅达到2.22 m，约为普通跑步引起振动的11倍，直到荷载作用结束后，其变化规律同普通跑步振动类似。相比跑步荷载，行人跳跃导致悬索桥共振时，结构变形进一步增加，其峰值达到3.30 m，约为普通跳跃荷载的8倍，远大于其他类型荷载作用下结构的变形。

(2) 当结构发生跑步共振时，加速度响应变化与结构变形响应类似，随跑步荷载的作用逐渐增大，并在平衡点附近做近似周期性的往复运动，其幅值约为16.40 m/s2，在荷载结束后结构加速度逐渐减小，减小速度较普通跑步振动缓慢得多。结构跳跃共振时，加速度响应曲线虽有些许突变，但其变化规律大体上同变形响应曲线一致，其峰值达到27.16 m/s2。

(3) 跑步共振时加劲梁的最大应力增加至239 MPa，跳跃共振时增加至358 MPa，分别为最不利人群荷载工况下的2倍和3倍。

3.5 人行荷载工况对比

针对悬索桥各个工况的分析结果汇总如表2所示，其中工况Ⅰ为满跨均布人群荷载，工况Ⅱ为半跨均布人群荷载，挠度、应力及加速度代表对应工况下加劲梁最大挠度、应力及加速度。

表2 各个工况下结构受力特征

从表2可以看出：不同工况下，结构的应力及挠度差异较大，对比两种人群均布荷载工况，工况Ⅱ(半跨均布荷载)对结构更为不利。对比工况Ⅱ与普通人行荷载工况下结构的受力特征，数据表明，行人的跑步与跳跃荷载对人行悬索桥的影响不能忽略不计，单纯考虑人群均布荷载的设计理念，对于景区人行悬索桥复杂的受力环境而言，存在较大的安全隐患。挠度方面，相较于普通行人激励荷载工况，工况Ⅱ使结构产生的变形最大(0.55 m)，跳跃荷载工况其次(0.42 m)，跑步荷载工况最小(0.21 m)；从应力来看，3种工况下结构的应力差距较小，跳跃荷载工况下加劲梁应力为146 MPa，已超过工况Ⅱ下加劲梁的最大应力(117 MPa)，跑步荷载工况下应力最小(90 MPa)。

相比普通人行荷载，在偏心人行荷载作用下结构的应力及挠度有所提高，其中，在横向不对称跳跃荷载下加劲梁的挠度达到0.61 m，应力为190 MPa，均超过上述其他工况下结构的应力及变形，并使桥面产生较大倾斜，可见横向偏心人行荷载对该悬索桥而言更加不利，应当予以注意。由于悬索桥结构本身抗扭刚度较低，为抵抗横向不平衡荷载，从设计上来说可以通过增加截面刚度、设置阻尼器等方式来提高结构刚度，减小桥梁在扭矩下的变形。但从安全角度出发，游客在栏杆附近嬉戏打闹这一行为本身就较为危险，此外，偏心荷载会造成桥面的倾斜，进一步增加行人失足掉落的可能性，针对这种特殊的荷载工况，单纯从力学上入手，提高结构的抗扭刚度既不经济也不科学，应当在管理运营方面，增强游客的安全意识，这样既能保证游客游玩时的人身安全，又能防止较大横向偏心荷载的发生，改善结构的受力性能。

共振时，悬索桥的应力及变形大幅增加，从而会导致结构的破坏。其中，跳跃共振对结构显然更为不利，结构最大挠度达到各个工况下的最大值(3.30 m)，最大应力为358 MPa，远超过加劲梁的设计强度。跑步共振时结构的最大挠度增长至普通跑步荷载下最大挠度的10倍以上，应力亦增至239 MPa。然而如前文所述，由于行人跳跃荷载的频率变化范围较小，而人行悬索桥属于长周期结构，频率较平均跳跃荷载而言往往更小，发生共振的概率相对较低，故而建议在景区人行桥设计中应当更关注跑步共振的情况，针对这一工况进行相应计算，或是在设计中对静力分析结果乘以2的安全系数，以保证结构的安全性。

另外，由于结构整体刚度较小，在人行荷载作用下，结构振动的峰值加速度普遍较大，共振时，峰值加速度的增长相对较小。美国AISC标准曾对楼板结构在节律性荷载下结构的峰值振动加速度给出了一定限值，然而这主要是考虑到普通建筑结构中居民在居住办公时的舒适性要求，而非结构力学性能上的考量。对于人行桥，结构的振动加速度并没有非常严格的规定，日本的小跨径悬索桥设计规范中也仅针对有汽车通行可能的结构，考虑到车辆行驶的平稳性，对结构的最大挠度进行了限制。事实上就景区人行悬索桥而言，在结构安全范围内，适当振动更能增添游客游玩时的乐趣性，过于苛刻的舒适性要求并没有太大意义。

4 改善景区人行悬索桥受力性能的措施及建议

4.1 改善景区人行悬索桥受力性能的结构形式

景区人行悬索桥相较于其他桥型而言，结构刚度较小，周期更长，在振动及荷载(特别是不均匀荷载)作用下，往往产生更大的变形，也使得加劲梁处有较大的应力。常规的提高悬索桥刚度的方法往往是增大加劲梁面积，从而减小主梁的应力及变形[13]，然而这将大大提高钢材的用量增加结构造价，对于一座景区的人行悬索桥而言显然不经济。该文尝试通过将普通单链悬索桥修改为双链的方式，提高结构的刚度，改善悬索桥的受力性能。

双链悬索桥是在一个吊杆平面内设有两条主缆的悬索桥，两条主缆在跨中交叉且相互联结，上下主缆在全跨范围内均匀布置有吊索吊拉加劲梁。当桥梁半跨有活载时，荷载将由该半跨的下链及另外半跨的上链共同承受，大大抑制结构的S形竖向变形，相比单链悬索桥显示出大得多的刚度。在上述人行悬索桥的基础上，保持跨径、矢高、材料特性等结构参数不变，在吊杆平面增加一条主缆，并通过悬索桥半跨的初始平衡状态分析求得主缆线形，即得到相应的双链悬索桥模型。

采用相同的方法对该悬索桥进行特征值分析，前10阶自振特性如表3所示。由表3可以看出:由于索结构数量的增加，在结构前几阶模态中以主缆振动为主的模态数量大大增加，结构第1阶竖向振型出现在模态14，其频率约为0.885 8 Hz。

表3 双链悬索桥自振特性

分别对结构在人群荷载、行人跑步荷载及行人跳跃荷载3种工况下结构的受力性能进行分析，其最大挠度Δ，加劲梁最大应力σ，加劲梁最大加速度a及较单链悬索桥相应分析结果比值f如表4所示。

表4 双链悬索桥受力特征

由表4可知：

(1) 在最不利人群均布荷载作用下，双链悬索桥加劲梁跨中位置应力最大，为71 MPa，约为单链悬索桥最大应力的61%，而最大挠度在1/4跨径位置，为0.16 m，仅为单链悬索桥的29%。可见，通过将单链悬索桥改为双链悬索桥，能够在不增大加劲梁面积的情况下，大大增加结构的整体刚度，从而减小结构的变形，改善结构的受力。

(2) 结构在动力荷载作用下的变形及加速度响应变化规律同单链悬索桥基本一致，然而由于刚度的增加最大位移相比普通悬索桥大大减小。结构在跑步荷载工况下的最大变形为0.05 m，而在跳跃荷载工况下为0.11 m，仅为相应荷载工况下单链悬索桥的1/4。

(3) 在跑步荷载工况下结构的最大加速度为7.86 m/s2，较单链悬索桥更小，但在跳跃荷载工况下结构的最大加速度为21.81 m/s2，稍大于单链悬索桥。

(4) 在跑步荷载作用下加劲梁的最大应力为71 MPa，略小于单链悬索桥在跑步荷载下的受力，而在跳跃荷载作用下则为158 MPa，较单链悬索桥而言稍大，其变化规律同结构的加速度变化规律一致。

4.2 相关建议

综上所述，对于景区人行悬索桥这一特殊桥型而言，荷载工况复杂，根据对各个工况下的受力分析，提出以下建议：

(1) 在人行荷载特别是行人跳跃荷载作用下，结构会产生较大的应力，特别是结构发生共振时，应力与挠度将大幅增加，可能导致桥梁的倒塌，以往在设计中仅考虑人群荷载作为控制应力的方法存在一定的安全隐患，故而在设计选取控制应力时应针对相应的人行荷载进行分析对比，以求得最不利工况，保证结构在运营期间的安全性。

(2) 人行偏心荷载相比普通人行荷载而言更为不利，但考虑到行人游玩时的安全，可以从景区管理的方面出发，如设立相关警示标识、增设管理人员等方式提高游客安全意识，避免相关荷载工况的发生。

(3) 双链结构在不增大加劲梁面积的前提下，极大地提高了人行悬索桥的竖向刚度，针对人行荷载这一竖向激励而言，能够改善结构的受力性能，经济合理，有一定的推广价值。

5 结论

以某景区人行悬索桥为例，针对各个工况进行了结构力学性能研究，完善相应设计理念，并对比分析了单、双链悬索桥的受力特征，得到如下结论：

(1) 就景区人行悬索桥而言，相比人群荷载，特殊人行荷载对结构的影响较大，不可忽略，应在设计中予以重视，其中，跳跃荷载对于结构更为不利，在仅15人的跳跃荷载作用下，加劲梁的最大应力已经超越了最不利人群荷载工况下结构的最大应力。

(2) 相比普通人行荷载，人行偏心荷载对结构更加不利，同时会使桥面产生较大倾斜，可能造成游客失足，设计上可以通过增大加劲梁截面、设置阻尼器等方式增大截面的抗扭惯矩，但考虑到经济性和必要性，建议从管理方面入手，提高游客安全意识，避免此类荷载工况的发生。

(3) 行人激励荷载与结构发生共振时，加劲梁应力及变形会大大增加，甚至可能导致人行悬索桥的倒塌。跳跃共振虽更为不利，但发生概率较小，设计中应当更关注跑步共振的情况，建议针对景区人行桥进行相应工况的计算或对静载结果乘以2的安全系数。

(4) 双链悬索桥能够在不增大加劲梁面积的前提下，提高结构的整体刚度，大大减小结构在人群均布荷载等静载及较小动力作用下的应力及变形。而在行人跳跃等较大动力荷载作用下，由于悬索桥刚度的增大，结构振动反而可能产生更大的应力，但就结果来看，双链结构仍能以较小的应力增加换取变形的大大降低，综合而言，对景区人行悬索桥的受力性能的提高是有利的。