公路软岩边坡稳定性及支护设计优化研究
2022-05-14严琼张化进吴顺川侯圣均
严琼, 张化进, 吴顺川,3, 侯圣均
(1.中电建路桥集团有限公司, 北京市 100048; 2.昆明理工大学 国土资源工程学院, 云南 昆明 650093; 3.北京科技大学 土木与资源工程学院,北京市 100083)
1 前言
深挖路堑边坡稳定性及支护方案一直是路基工程中重点关注的问题,如何设计出安全合理的边坡工程开挖支护方案基于可靠的稳定性评价方法。近年来,强度折减法在边坡稳定性分析领域得到广泛应用,其实质是通过不断折减岩土体抗剪强度参数,直至边坡恰好达到临界破坏状态,进而探究边坡失稳破坏机理,凭借其简明的理念及可直观获得临界滑面及其相应安全系数等特点,该方法在边坡稳定性分析领域,尤其是数值计算方面,起着至关重要的作用。
强度折减法可综合边坡体本构关系、应力变形作用、支护结构效应等性质,一直是边坡设计及其优化的重要技术手段。李建宇等[1]基于FLAC3D内置强度折减法对路堑高边坡锚索支护方案中的关键支护参数进行了设计优化;余和广等[2]采用强度折减法分析了错落体治理前、后的位移与安全系数,为软弱夹层边坡支护方案提供依据。截至目前,基于等比折减理念的传统强度折减法在边坡领域应用已较为普及,但采用非等比强度折减法进行工程实例研究仍较少。
从力学机制出发,在边坡滑动过程中岩土体黏聚力和内摩擦角发挥作用的次序和程度均不相同[3],传统强度折减法对解决该问题是力所不及的,诸多学者对此开展了大量研究。李继兰等[4]借助强度折减法,采用正交试验分析了土体边坡稳定性影响因素的敏感性,其内摩擦角敏感性比黏聚力大;刘新喜等[5]针对软弱夹层的流变性质,提出考虑蠕变特性的强度折减法,研究边坡的长期稳定;唐芬等[6-7]基于前人对边坡稳定性影响因素的研究,提出了非等比强度折减法,对黏聚力和内摩擦角采用不同的参数进行折减,解决了强度参数差异性发挥作用的影响。在此基础上,近年来逐渐发展出双系数强度折减条分法[6]、非等比例相关联折减法[8]、基于临界曲线的双系数折减法[9]等,分别考虑了黏聚力与内摩擦角的影响,实现了从单系数向双系数折减的转变,丰富了边坡稳定性计算方法,弥补了传统强度折减法等比折减导致计算结果偏不安全的不足。
该文根据施工图纸、工程地质勘查资料及现场地质情况,基于“高边坡普查→提出优化设计分区建议→筛选重点边坡→重点边坡优化研究”的优化设计思路,在保证边坡稳定性基础上对云南省红河州建水(个旧)至元阳高速公路项目2标段的路堑高边坡进行优化研究,总体思路是:由于坡体岩性较好,可考虑优化锚杆和锚索等锚固结构,利用传统和非等比强度折减法,在保证边坡稳定的基础上,同时减少工程成本,实现经济与安全并重的目的。
2 工程地质条件与边坡设计方案
红河州建水(个旧)至元阳高速公路项目是云南省规划“五纵五横一边两环二十联”中南部高速公路网的重要组成部分,是省高网“十三五”新开工重点项目,对解决滇南地区的交通快速通道不足等问题具有重要意义。项目分为两段:建水至元阳、个旧至元阳高速公路,项目全长分别为73.256、51.542 km,全线采取高速公路技术标准,按照双向四车道建设,设计速度80 km/h,桥梁、隧道占路线总长70%以上,其余路段基本为高填深挖路段,全线路堑开挖高度大于30 m的高边坡达58处,是一条极具云南省山区建设特点的山岭区高速公路。
K10+900~K11+080段边坡位于建(个)元高速公路2标(建水至元阳段),该深挖路堑段地貌总体为溶丘洼地型地貌,微地貌为一宽缓山脊,地形坡度一般为20°~25°,相对高差为50~100 m。路基主要横跨山体斜坡,在山坡部位大部分有第四系坡积层分布,山坡中上部基岩出露,基本为强风化、中风化软质岩层。
该边坡沿走向两侧地形均较平缓,不存在安全隐患,因此仅需研究边坡在倾向方向开挖后的稳定性。因该边坡内部岩体风化程度较高,呈碎裂结构,无优势结构面,且岩土分界面在边坡各开挖剖面上分布形态相似,故以坡高最高的剖面(K10+940)作为研究对象,边坡高度33.13 m,为4级开挖边坡,设3个台阶,台阶宽度分别为2、4、2 m,边坡坡率为1∶1.25、1∶1、1∶0.75、1∶0.75(从坡顶到坡底设计路面),如图1所示。

图1 K10+940路堑边坡加固设计方案(单位:m)
根据地面调查、物探及钻探成果,场区出露地层从上至下分别为第四系全新统坡积层及泥盆系中统东岗领阶曲靖段,各地层具体情况如下:
(1) 第四系全新统坡积层
红黏土:红褐色,硬塑状,稍湿。根据钻孔CLJZK7揭露的覆盖层详细描述如下:CLJZK7钻孔位于拟开挖边坡下部,揭露覆盖层红黏土厚1.6 m,硬塑状,稍湿;覆盖层厚度较大区段主要分布在山坡坡脚及洼地。
(2) 泥盆系中统东岗领阶曲靖段
岩性主要为灰白色灰岩。钻孔CLJZK7揭露的基岩描述如下:孔深1.6~15.4 m,灰岩,深灰色,中风化,厚层状,岩芯呈柱状、短柱状、碎块状;其中7.1~13.6 m溶蚀强烈,溶隙发育,溶隙内充填红黏土,岩芯破碎,呈碎块状。
根据以上地勘资料和现场钻孔分析,以及邻近工点岩石物理力学试验及工程经验,可知该段山体上覆层均为红黏土,坡体上部覆盖层1~2 m,中下部坡脚及冲沟内厚度较大,分析认为厚度约10.0 m。场区内岩土物理力学性质建议设计参数见表1。原锚索支护设计方案主体为锚杆(索)框架梁,如图1所示,加固支护参数见表2。
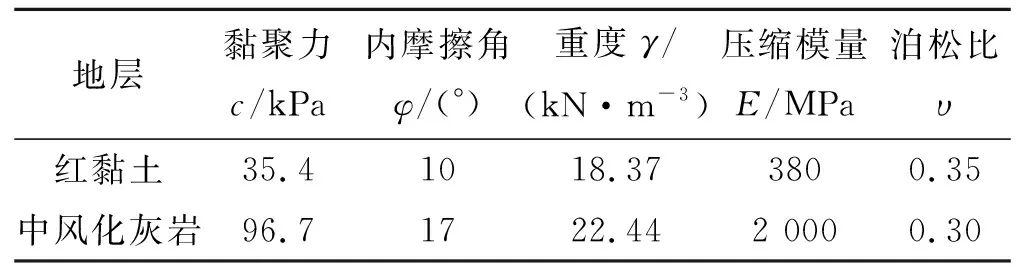
表1 K10+940路堑边坡开挖数值计算模型物理力学参数
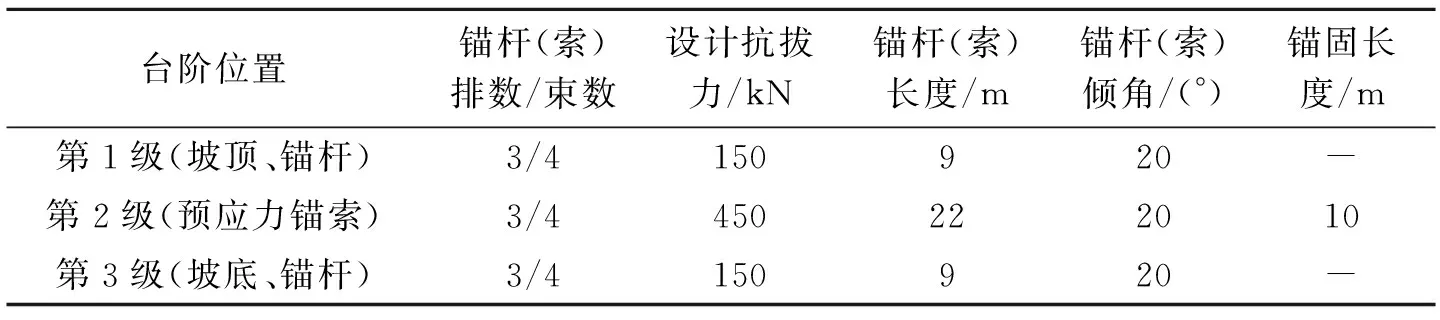
表2 K10+940路堑边坡逐级开挖加固支护参数
3 边坡开挖支护数值模型建立
FLAC3D有限差分法数值计算原理是采用网格节点传递力和位移,并可考虑岩土体大变形的数值计算常用工具[10]。根据地面调查、物探、钻探成果及设计文件,基于FLAC3D模拟程序按照原地面线及开挖工况状态建立数值模型,如图2所示,未开挖时划分为2 136个单元,4 432个节点,开挖后边坡划分为1 734个单元,3 660个节点。

图2 K10+940路堑边坡开挖初始数值模型(单位:m)
边坡岩土体采用摩尔-库仑本构模型,计算模型采用如下假定:
(1) 路堑开挖坡体为连续、均质、各向同性的线弹性材料。
(2) 边坡体各层间及加固材料之间完全连续,无脱空现象。
(3) 边坡体各层间及加固材料之间位移连续,位移边界条件为左、右侧法向约束、底端固定约束。
经过初始模型试算,位移达到收敛后,开挖后锚杆(索)加固支护数值模拟的稳定性状态如图3所示。最大剪应变增量仅2.88×10-4,出现在预应力锚索支护位置,边坡体内未形成潜在滑动面,第2级边坡产生的剪应变增量是由预应力锚索张拉造成的,同时也引起预应力锚索部分应力损失。由图3(b)可知:边坡内锚杆(索)轴向应力分布正常,未出现破坏失效现象。经FLAC3D内置的传统强度折减法分析,该边坡支护后较稳定,安全系数达1.42,大于1级边坡要求设计安全系数(锚固支护规范一级边坡1.25~1.35[11],公路设计规范1级边坡1.20~1.30[12])。综上,该边坡具备可优化的条件。

图3 K10+940路堑边坡支护后稳定性状态云图
4 锚杆支护设计优化前后对比分析
4.1 支护结构优化方案
边坡失稳破坏往往是从坡脚处开始出现破裂,不断向坡体内部扩展的演化过程[13]。因此,在满足设计安全系数要求(1.25~1.35)的基础上,从边坡上部坡面开始,逐级向下进行支护结构优化,流程如图4所示。

图4 支护结构优化流程图
针对该边坡的支护结构,拟建立以下加固支护优化方案,且每一优化步骤须在满足设计安全系数要求基础上进行。
第1步:开挖到第2级台阶处,开挖深度13.13 m,取消第3级边坡锚杆支护。
第2步:开挖至第1级台阶处,开挖深度23 m,取消第2级边坡预应力锚索支护,改为锚杆支护。
第3步:在第2步基础上,继续取消第2级边坡锚杆支护。
第4步:开挖至设计路面,开挖深度33 m,取消第1级边坡锚杆支护。
为了证实上述优化方案的合理性和可靠性,该文分别采用传统强度折减法(等比折减)和非等比强度折减法进行边坡稳定性分析。
4.2 传统强度折减法
英国学者Bishop提出强度折减技术是把潜在滑动岩土体抗剪强度参数折减至临界状态,此时的折减系数Fs即为安全系数[14]。传统强度折减法自提出以来,广泛应用于边坡数值分析过程中,黄庆等[15]基于FLAC3D强度折减法研究了厚覆盖层边坡失稳破坏模式;刘新喜等[16]采用强度折减法分析了软岩路堑边坡稳定性状态,确定了软岩路堑边坡变形破坏特征。目前,强度折减法一般假定黏聚力c和内摩擦角φ两抗剪强度参数按照同比例进行折减,即:
(1)
式中:c′、φ′为折减后边坡临界状态时对应的黏聚力、内摩擦角。
按照支护结构优化方案,依据传统强度折减法,对比各级边坡支护优化前后的整体安全系数和锚杆(索)受力(表3),边坡优化前后的稳定性状态均较好。

表3 各级边坡支护优化前后的稳定性状态
根据优化前后的位移和剪应变增量云图(图5、6),从位移上看,边坡支护结构仅能减小坡面上部分位移,且为毫米级别,对边坡稳定影响不大;从优化前后最大剪应变增量图的潜在滑面来看,取消所有锚杆(索)后,边坡的潜在滑面位置虽显著上移,安全系数从1.42降低至1.36,但仍满足设计安全系数要求。

图5 优化前后坡体位移云图(单位:m)

图6 优化前后边坡最大剪应变增量图潜在滑面及安全系数
上述宏观安全系数的分析结果表明:该边坡可取消所有支护结构,减少支护成本。
4.3 非等比强度折减法
大多数学者[17-18]的研究表明:在边坡实际滑动过程中,黏聚力与内摩擦角发挥的作用及其先后顺序均不同,衰减速度也不同。因此,在边坡稳定性分析过程中,以上两个强度参数应按不同比例折减进行数值模拟计算。随着非等比强度折减法的引入,有效弥补了传统强度折减法黏聚力与内摩擦角等比折减可能导致计算结果偏不安全的问题。因此,结合以上机理,为进一步验证优化方案的可靠性,该文针对优化后的边坡模型,采取非等比强度折减法进一步确定边坡的安全储备是否满足设计安全系数要求,为该边坡支护结构优化方案提供对比验证和理论依据。
由于非等比强度折减法采用两个不同的折减系数,两折减系数间有无数种组合方式,且不同的强度折减方式可能显著影响边坡稳定性分析结果[3]。结合近期研究结果,该文采用目前较为广泛的几种非等比强度折减方式及综合安全系数,分析优化后的边坡稳定性状态,判断支护结构优化方案的可行性。
黏聚力和内摩擦角折减系数分别为FSc,FSφ,公式如下:
(2)
(3)
根据该边坡几何特征,计算整体边坡坡度约为42°,坡率约为1∶1.11,结合文献[19]的研究成果,边坡坡角小于45°时,由摩阻力充分发挥主导作用,且黏聚力发挥作用较内摩擦角滞后,因此,φ的折减系数FSφ应小于c的折减系数FSc,将两折减系数的比值称为非等比折减系数η,即η=FSc/FSφ。唐芬等[3]、Yuan等[20]认为非等比折减系数η与边坡坡率/坡角相关,并给定了若干个边坡坡率/坡角对应的非等比折减系数η,根据边坡几何特征,利用插值法可获得该边坡的非等比折减系数η,η1=1.02,η2=1.05,计算综合安全系数见表4。

表4 不同研究成果下计算的综合安全系数
根据潘家铮[21]最小值原理,滑坡失稳时将沿抵抗力最小的滑面破坏,即边坡总是以最有可能的劣化路径失稳。袁维等[9]、Isakov等[22]定义初始强度参数M0折减至临界状态曲线的最短距离为最有可能性失稳路径,亦称为最短路径Rmin,该方法无须假定两强度参数的比例关系,便可反映边坡最可能的破坏方式。根据计算分析,该边坡的不同折减路径临界状态曲线如图7所示,其中Rt为传统强度折减法对应的折减路径长度,Mmin为该边坡最有可能失稳的临界状态,对应的FSc=1.44,FSφ=1.24,η=1.16,经综合安全系数计算后,计算的综合安全系数分别为1.34、1.35(表4)。
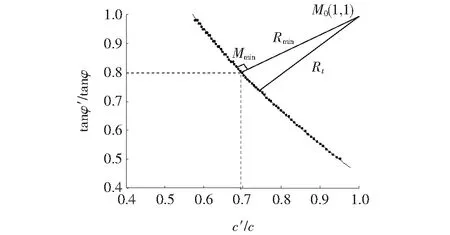
图7 边坡稳定性分析的强度折减最短路径图
综上所述,采用非等比强度折减法计算优化后的边坡综合安全系数均为1.35左右,满足1级边坡安全等级设计安全系数要求(1.25~1.35)。
由此,通过传统强度折减法和非等比强度折减法的边坡稳定性分析对比验证,进一步证明该边坡施工过程中,可对其设计方案进行优化,取消所有锚杆(索)支护结构,减少工程成本。
4.4 优化效果评价
经充分的试验研究、理论分析和计算机数值模拟研究,分析了优化方案后的边坡稳定性状况,在此基础上,采用优化方案对施工设计进行调整与变更。
从安全角度看,按优化方案施工后,边坡安全系数符合设计安全系数要求,且自开挖以来,坡体未出现变形、开裂等潜在失稳现象,路堑边坡处于稳定状态,表明该优化方案是可靠的。其次,边坡支护设计优化后节省了大量锚杆(索)结构,对该项目降低施工成本和缩短施工工期具有十分重要的意义。
5 结论
结合红河州建水(个旧)至元阳高速公路项目,以2标段K10+900~K11+080段左侧路堑边坡为工程背景,对该边坡支护系统的设计优化方案展开分析,得到以下结论:
(1) 基于工程地质调查及数值模拟计算,分析优化前边坡的稳定性状态,可初步确定边坡具备优化的条件。
(2) 结合边坡施工工况,采用自上而下的支护结构优化方案,对比优化前后的宏观安全系数、位移和剪应变增量云图潜在滑面等边坡稳定性指标,可获得边坡设计优化的基础理论支持。
(3) 通过对比传统强度折减法和非等比强度折减法在支护结构优化前后的边坡稳定性状态,进一步证明该边坡取消所有锚杆(索)支护结构这一优化方案的可行性。
