基于双模型的农业用水量预测算法仿真

任永泰，王如意

(1. 东北农业大学理学院，黑龙江 哈尔滨 150030；2. 东北农业大学工程学院，黑龙江 哈尔滨 150030)

1 引言

水资源是工业、农业以及畜牧业等多个领域发展的前提要求[1]，但全球水资源分配不均使多个国家水资源较匮乏，且我国南北水资源分配严重不均。随着国家不断发展，人们生活水平提高，各个方面的需水量大大增高，而地球的水资源有限，其中农业是用水量较大的一个行业，若不合理运用极可能导致附近水资源枯竭[2]，预测农业用水量，则可均匀分配且提前解决水源枯竭的问题，进而推动农业持续发展[3]。

乔俊飞等人[4]提出基于尖峰自组织模糊神经网络的农业种植区域用水量数据化预测算法，该算法将用水量数据通过主成分分析进行降维处理，同时计算出线性无关的用水量数据主成分变量，将其视为用水量预测模型的输入数据，其次构建用水量预测模型，在尖峰强度和误差指标的要求下对隐含层神经元进行训练，并融合Leveberg-Marquardt算法将预测算法简化，进而实现农业种植区域用水量数据化预测。但是该算法在进行农业用水量预测前没有对数据进行预处理，导致其中冗余数据以及缺失数据过多，因此在预测用水量过程中需要用大量时间筛选无用数据，无法贴合实际值且极可能将缺失数据错误预测，进而降低预测拟合度。邓权龙等人[5]提出基于小波分析以及灰色预测模型的农业种植区域用水量数据化预测算法，该算法首先利用小波分析方法在不同尺度下将农业种植区域用水量时间序列进行分解，在此基础上通过灰色预测模型对农业种植区域用水量进行预测，实现了农业种植区域用水量数据化预测。但是，该算法没有提前对数据进行清洗以及归一处理，无法生成较为简单且干净完整的数据，致使数据利用率较低，因此需要更多的数据进行计算，不仅加大计算量，也过于浪费时间，进而升高预测复杂度。王亦斌等人[6]提出基于EMD-LSTM模型的农业种植区域用水量数据化预测算法。该算法首先运用中值滤波方法对用水量数据序列进行滤波的预处理，其次利用EMD方法分解用水量数据序列，同时将分解后的特征序列利用LSTM模型预测农业种植区域用水量，最终将所有数据序列的预测值进行叠加，获取完整的农业用水预测值，实现农业种植区域用水量数据化预测。但是，由于该算法没有归一化处理数据后再进行用水量预测，而是对数据进行滤波处理后进行预测，虽减少了部分数据，但数据量仍较大，生成大量的计算极有可能出现不必要的错误，进而升高相对误差，从而降低预测可靠度。

为解决上述方法中存在的问题，提出农业种植区域用水量数据化预测算法。

2 用水量数据预处理

为保证农业用水量预测值足够准确，需要提前对原始数据进行数据清洗等预处理，保证数据中无错误数据，同时确保数据完整，进而提高预测精度[7]。

2.1 数据清洗

通常情况下对数据的简单筛选无法获取简单且干净完整的数据，当数据过于复杂，极容易将用水量极小的流量数值视为0，这时就可能将这种异常缺失数据忽略，进而使得最终数据不完整，导致预测值准确性大大降低，因此需要清洗数据，清洗数据指的是删除错误数据以及缺失数据或者填补缺失数据[8]，防止删除了有用数据，因此选用填补缺失数据的方式对数据进行清洗，填补缺失数据即将全部完整的用水量数据的算数平均值当成缺失数据的缺失值进行填补，但直接进行填充大概率会对缺失数据以及其它数据的关系造成影响，其中尖峰部位的用水量数据极易出现误差，因此需要对相邻两天内的用水量数据均值进行填补，同时填补每个时间段相邻两个时间点的用水量数据的均值，则在K-最近邻法性质的基础上根据水资源的周期特性得出的填补公式为

Xi=α1[(Xi-24*60/5+Xi+24*60/5)/2]+α2[(Xi-1+Xi+1)/2]

(1)

式中，Xi代表目前时间段内用水量流量的代替值，Xi-1代表目前时间的前5分钟用水量数据，Xi-24*60/5代表头一天同时刻的用水量数据，Xi+24*60/5代表后一天同时刻的用水量数据，α1和α2均代表填补公式的加权系数，且两个系数之和为1。

利用此公式即可将用水量数据中的缺失数据进行填充，进而获取完整的用水量数据。

2.2 用水量数据归一化处理

获取到完整全面的数据后为简化用水量预测步骤需对数据进行归一化处理，数据的归一化实质是一种线性变换数据，简化计算过程的同时提高数据训练速度，加强用水量预测效率[9]。首先在极值归一化的基础上将清洗后的数据压缩至区间[0，1]内，在用水量序列中提取每段时间内的用水量最大值和最小值，分别将其记为xmax和xmin，根据归一化公式对用水量序列进行处理后得到新的用水量序列表达式为

x′=(x-xmin)/(xmax-xmin)

(2)

式中，x表示原始用水量序列，x′表示归一化处理后的用水量序列。

3 农业用水量数据化预测

为准确预测农业种植区域用水量，利用灰色预测模型以及三次指数平滑预测模型叠加形式进行预测[10]。

3.1 构建灰色预测模型

灰色预测是利用历史信息和对未来信息的估计描述目前用水情况，灰色预测模型的优点是可利用较少数量的数据进行计算即可得出相关性极强、而离散性较小、且预测数值拟合程度高的用水量。

假设农业初始用水量序列以及叠加一次后的序列分别为

(3)

其中，x0代表原始农业种植区域用水量序列，x1代表经过叠加后的农业种植区域用水量序列，t表示常数，且t=1，2，…，n。

根据x0和x1构建出关于灰色预测模型的白化微分表达式为

dx1/dt+ax1=u

(4)

式中，u代表方程式的灰色作用量，a代表方程式的发展系数。

通过最小二乘法对灰色作用量和发展系数进行求解，同时利用Laplace转换法获取时间回应，且将时间回应进行离散后得出的表达式为

(5)

消除式(5)中的叠加得到的表达式为

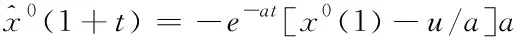
(6)

将时间回应表达式进行还原后即为构建了灰色预测模型。

3.2 构建三次指数平滑预测模型

在预测农业种植区域用水量时会出现用水量偏低情况，此时的用水量容易被忽略，而指数平滑预测算法就可预测用水量较少的情况，指数平滑预测算法包含一次、二次以及三次平滑预测，由于农业种植区域用水量处于一直下降的趋势，因此选用三次平滑预测模型进行预测[11]。

假设目前用水量的时间序列是由n个历史用水量数据构成的，其表达式为

X={X(1)，X(2)，…，X(n)}

(7)

则根据时间序列X即可得出三次指数平滑预测模型表达式为

(8)

其中，S1(t)代表预测用水量的第t期中第一次指数平滑预测数值，S2(t)代表预测用水量第t期中的第二次指数平滑预测数值，S3(t)代表预测用水量第t期中的第三次指数平滑预测数值，α代表三次指数平滑预测模型中的权数，且α在区间[0，1]之间，X(t)代表预测用水量第t期内的实时用水数值，Y(T+t)代表预测过程中第(T+t)期中的农业用水量预测值，a(t)、b(t)以及c(t)均代表预测模型中的平滑系数。

3.3 预测模型组合方法

假设{xt，t=1，2，…，N}是农业种植区域用水量评价指标序列的实时数值，令预测模型数量为m，则将m个预测模型中的同一时间t的预测值进行组合后得到的预测值为xit，在加权算法平均组合预测原理的基础上得出农业种植区域用水量预测模型组合模型的表达式为

(9)

3.4 用水量的不确定性处理

用水量的不确定性处理即在贝叶斯定理的基础上修改农业种植区域用水量预测值的先验概率密度[12]。

假设农业种植区域用水量从开始到结束的过程是k阶马尔科夫过程，且w0为前k天实际农业种植区域用水量，令预见期为n，则n的预测变量wn的先验概率密度为g(wn|w0)。

当预测用水量的时间是固定不变的，则利用组合预测模型得出的关于预测变量wn的预测值似然函数是f(sn|wn，w0)，而似然函数虽可表示组合模型的用水量预测性能，但先验概率密度以及似然函数都不能对用水量最终的预测值进行修改，因此关于w0得出最终用水量预测值的期望密度表达式为

(10)

则预测变量wn的后验密度表达式为

(11)

其中，φ代表预测变量wn农业种植区域用水量不确定性的固定描述，k代表经过归一化后的常数。

最终利用式(11)即可求出最准确的农业种植区域用水量预测值，同时将预测值进行还原即可实现农业种植区域用水量数据化预测。

由于简化了预测过程，将训练样本数据进行了归一化处理，因此最后训练出的结果也具有归一特性，不是真正的农业种植区域用水量，需要对其进行反归一化处理，则反归一化处理的数据公式为

x=xmin+y·(xmax-xmin)

(12)

式中，y代表所要预测的用水量的时间，x代表经过反归一化处理后的真实用水量预测值。

4 实验与结果

为验证所提方法的整体有效性，需要对农业种植区域用水量数据化预测算法(所提算法)、基于尖峰自组织模糊神经网络的农业种植区域用水量数据化预测算法(文献[4]算法)和基于小波分析以及灰色预测模型的农业种植区域用水量数据化预测算法(文献[5]算法)进行预测拟合度、预测复杂度和预测可靠度的测试。

4.1 预测拟合度

利用三种不同的农业种植区域用水量预测算法在不同时间段内进行用水量的预测，比较三种算法的拟合度，拟合度是检验预测模型的重要指标，其实质即为预测值与实际值的吻合程度，实验结果如图1所示。

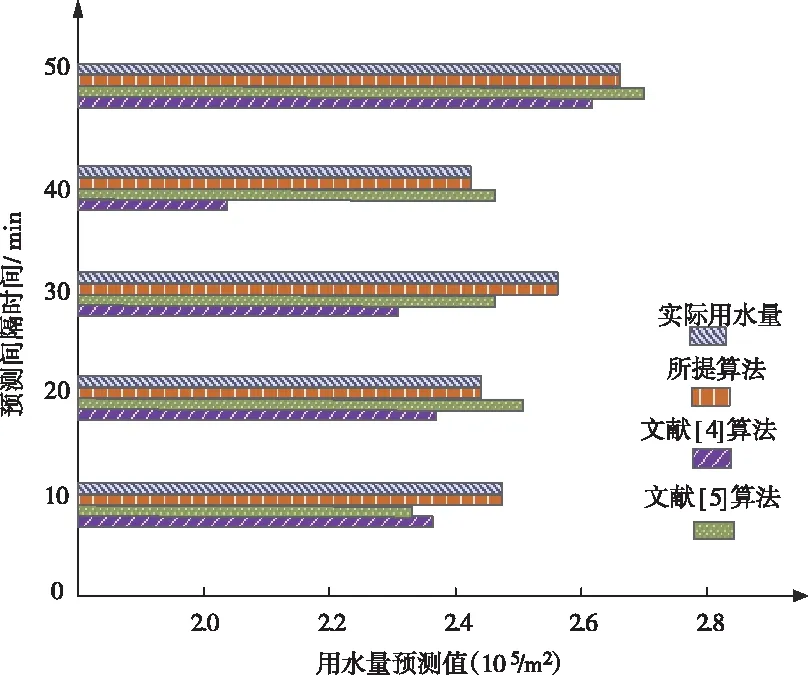
图1 不同算法的预测拟合度

根据图1可知，所提算法的拟合度最高，基本与实际用水量相同，文献[4]算法的拟合程度过高，即过拟合，导致分配给农业种植区域的水量过多，其它区域水量过少，进而出现分类不均的问题，而文献[5]算法的拟合程度过低，极可能出现用水量不够的问题，只有所提算法最适合用水量的预测，这是因为所提算法在进行农业种植区域用水量预测前先对数据进行预处理，消除冗余数据，填补缺失数据，使得预测过程中不需要一边运算一边筛选数据，直接将所有有用数据进行填充，因此更加贴合实际值，进而提高预测拟合度。

4.2 预测复杂度

利用农业种植区域用水量预测模型进行预测时必须与数据量为基础进行计算，但大多预测模型要求的数据量过高，导致运算量过大，造成预测过于复杂，在多次迭代下比较三种算法预测出准确结果后所需的数据量。如图2，每种算法中的不规则五边形面积即为迭代后所需的所有数据量，

图2 三种算法的预测复杂度

根据图2的实验结果可知，所提算法的面积最小，文献[5]算法的面积最大，文献[4]算法的面积次之，说明所提算法的复杂度最低，即最容易预测出农业种植区域用水量，所提算法的复杂度如此低是因为所提算法首先对数据进行清洗以及归一化处理，提前生成较为简单且干净完整的数据，进而将数据利用率发挥到极致，不仅节约时间，同时降低计算量，且利用较少数据即可预测出农业种植区域用水量，因此降低预测复杂度。

4.3 预测可靠度

相对误差就是预测值与实际值中的绝对误差与实际值之间的比值，根据相对误差可直接反映出预测结果的可靠度，即偏离真实值的大小，三种算法的预测可靠度如图3所示。

图3 三种预测算法的预测可靠度

根据图3的实验结果可知，所提算法在任何预测结果下的相对误差都是最小的，其它两种算法相对于所提算法其相对误差都过高，尤其是文献[5]算法的相对误差，进而证明所提算法的可靠度最高，因为所提算法将数据提前进行归一化处理，利用归一化处理后的数据进行农业种植区域用水量的预测，不仅会降低计算量，也可简化计算过程，避免出现不必要的错误，进而降低相对误差，从而提高预测可靠度。

5 结束语

由于南北方蓄水量差异过大，因此需要控制农业种植区域的用水量，但农业中变化因素过多，导致农业用水情况波动较大，很多时候会出现蓄水量不够或蓄水过多的问题，为解决目前算法存在的问题，提出农业种植区域用水量数据化预测算法。该算法首先对数据进行预处理，其次构建两种农业种植区域的用水量预测模型，并将两种模型进行组合，计算出用水量预测值，从而实现农业种植区域的用水量预测，解决预测拟合度低、复杂度高和可靠度低的问题。但此算法还需进一步加强，消除模型本身局限性的影响，进一步降低预测偏差，使得预测模型趋近完美。