冷链物流多层级配送中心连续选址模型构建

李桂娥

(山西大学商务学院，山西 太原 030031)

1 引言

随着经济的迅猛发展，居民对生活质量的要求越来越高，更多人追求果蔬和冷鲜食品的新鲜品质，冷链物流需求日益提升。冷链物流作为一种特殊的供应链体系，包含产品从生产到出售前的所有环节，使容易变质腐坏的生鲜食品一直处于低温环境，既确保了货物的质量，又降低了损耗[1]。配送中心是物流网络内的货物中转场所，其主要功能是实现货物的配送，在物流供应链体系中占有重要地位，而合理的配送中心选址则可以缩短物流配送耗时，对冷链物流行业以及区域经济的发展产生巨大的推动作用。

冷链物流的高速发展吸引了广大学者对其展开研究，例如文献[2]以提升服务能力为目标，对冷链物流资源进行整合优化，将基于需求距离积的分配问题作为配送中心选址的目标函数，通过计算节点需求量和辐射半径，并在目标函数中添加距离权值，从而得到冷链物流配送中心选址数学模型，并利用自适应免疫算法对该模型进行求解，但是该方法的选址结果并不是最优结果，实际应用效果差；文献[3]为提高冷链物流配送效率，通过建立双层规划模型，对冷链物流的开放式车辆路径与配送中心选址进行优化。将物流中心选址作为决策目标，创建上层规划模型，制定初始配送中心选址方案，根据成本与损失构建下层规划模型，采用粒子群算法对该模型进行求解，实现配送车辆路径与配送中心选址的优化与调整，但是该方法存在选址效果差的问题。

尽管以上方法都对冷链物流中心选址问题进行了优化，但存在一定的片面性，为解决当前方法存在的问题，本文构建了冷链物流多层级配送中心连续选址模型。

2 冷链物流多层级配送中心连续选址流程

对于冷链物流体系来说，配送中心的选址非常关键，利用一定的评估标准评价备选地址，并从中选取最优配送中心，能够缩短配送时间，提高配送效率。在选择配送中心地址前，应充分遵循适宜性、协调性、战略性以及经济性等四个原则[4]，以降低配送耗时、节约成本。另外，冷链物流多层级配送中心的连续选址也会存在一些影响因素，比如：自然环境、交通条件、政策法规以及地价、区域等。

图1为一般情况下，冷链物流多层级配送中心连续选址的基本流程。

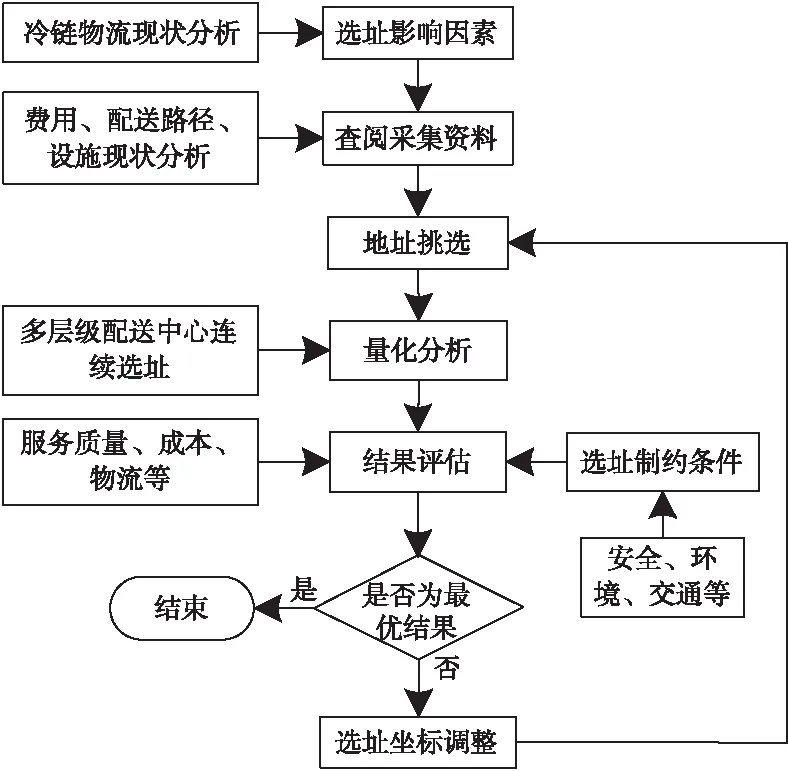
图1 选址基本流程

3 多层级配送中心连续选址模型构建

在构建多层级配送中心连续选址模型过程中，应对多种因素进行综合考量，若想在某一区域内为多个零售商提供合理的配送服务，那么物流配送中心选址要满足配送中心与各零售商的配送费用总额为极小值，且保证配送时长最短，因此以成本极小化为切入点，完成选址模型的构建。

构建多层级配送中心连续选址模型的基本条件如下：

1)根据运输量与运输距离构建运费函数；

2)一个零售商只匹配一个配送中心；

3)配送中心符合容量需求；

4)已知各零售商的需求量；

5)根据冷链物流系统内的零售商权重等级，优先为较大权重的零售商提供配送服务[5]；

6)采用地理坐标对配送中心与零售商的距离进行求解，并将其作为模型的配送中心与零售商距离数据。

3.1 基于配送费用最少的选址模型

将冷链物流的多层级配送中心i向零售商j配送产品的运输费用总额设为Cyij，j的坐标表示为(xj，yj)，i的坐标表示为(Xi，Yi)，两坐标之间的距离用dij表示，零售商j的数量表示为m，其需求量与允许配送的最大距离分别为pj与Dj，多层级配送中心i的数量为n，运输形式的数量为q。

基于不同的运输形式，多层级配送中心i与零售商j的货物运输费用表示为bijq(q=1，2，3，4)，其中，bij1表示航空运费，bij2为铁路运费，bij3、bij4分别表示公路运费与水路运费。若采用运输方式q，从配送中心i到零售商j的运输量设置为wijq，单位运输费用为aij，Zij用来指代i的配送服务范围，零售商的配送中心选择函数用y=e(x)表示，冷链物流配送范围的起始点坐标设定为(xa1，ya1)，其终止点坐标表示为(xa2，ya2)。

根据上述设定条件，构建配送费用最少的连续选址模型，其目标函数[6]如下所示

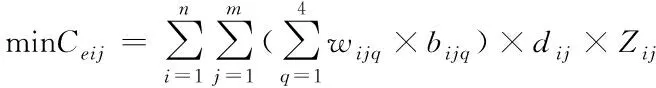
(1)

该目标函数的约束条件如下列各式所示

(2)

xa1≤Xi≤xa2

ya1≤Yi≤ya2

i=1，2，…，n

(3)

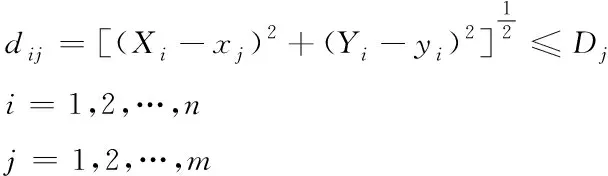
(4)

(5)

y0≥y=e(x)

(6)

3.2 基于配送时长最短的选址模型

设定配送中心i到零售商j的运输时长总和为Tyij，不同配送方式下，两地中每一段路程的运输速度及其运输难易程度，分别用γijq与vijq表示，各配送形式在物流配送路程中的占比用fijq表示，零售商的权值为λj。

根据上述设定条件，构建配送时长最短的连续选址模型，其目标函数如下所示

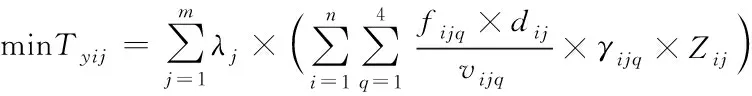
(7)

该目标函数的约束条件[7]如下列各式所示

xa1≤Xi≤xa2

ya1≤Yi≤ya2

i=1，2，…，n

(8)

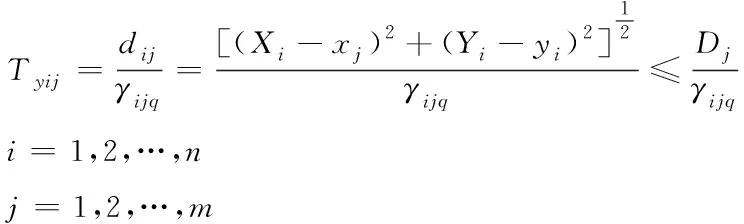
(9)

(10)

y0≥y=e(x)

(11)

4 多层级配送中心连续选址模型求解

在求解多层级配送中心连续选址模型过程中，需要将配送中心的连续选址问题转换成多源Weber问题，如果不考虑配送中心的容量限制，那么任意一个零售商的需求均会由距其最近的配送中心满足。通过分析选址目标函数，证明了其既非凹函数[8]，也非凸函数，这将导致大量局部最优解的生成。由于连续选址会形成许多局部最优解，而当前连续选址模型的计算方法通常是重心法，由于该方法获取最优解的复杂度相对较高，所以制定一种可以实现全局优化的策略具有非常重要的意义。

所以，本文选取启发式算法处理冷链物流多层级配送中心连续选址问题。多层级配送中心的连续选址不仅要同步确定多个配送中心，而且还要完成所有配送中心运输分配策略的制定，因此可以将该问题看做连续选址分配问题。

以运输费用最少的配送中心连续选址模型举例说明，通过以下两个步骤，完成选址模型的求解：

首先，如果不考虑约束条件中的时效性与安全性，只将运输费用最小化作为考量指标，那么应用配送费用最少的连续选址模型目标函数式(1)及其另外的约束条件进行选址，通过明确所有配送中心所负责零售商坐标集合，实现其分配矩阵的描述；

其次，如果将约束条件中的时效性与安全性考虑在内，那么采用MATLAB软件对目标函数进行优化，从而求解所有配送中心的选址模型，最终得到能够同时满足经济性、安全性以及时效性约束条件的连续选址策略。

4.1 交替分配启发式算法

基于已知的n个配送中心地址(X1，Y1)，(X2，Y2)，…，(Xn，Yn)，设定各零售商的需求供应点为距其最近的配送中心，各配送区域均可利用下式所示的零售商集合进行表述

Qi={j：min{dij}}

(12)

若想令运输费用为极小值，则要求解Xi与Yi的偏导数[9-10]，并使其为0。

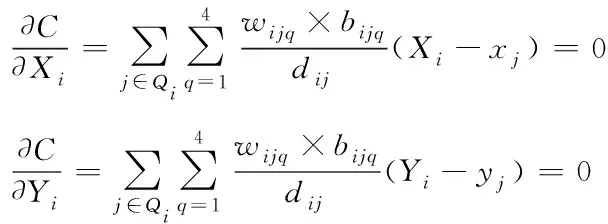
(13)

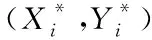
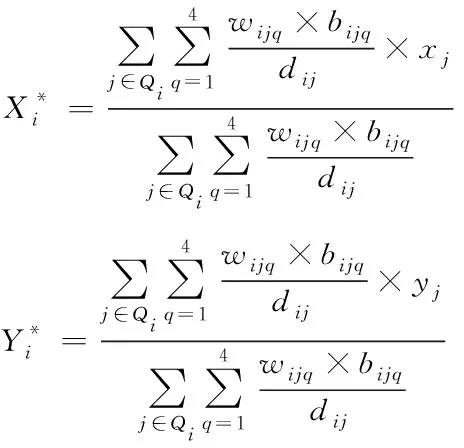
(14)

每种备选供应分配策略都用一个存在确定值的二进制数矩阵(lij)m×l来表示，备选策略数量为S(n，m)，其表达式如下所示

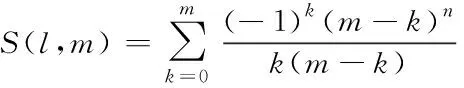
(15)

式中，k表示备选策略的描述性参数。若上式中的m、k增大，则说明备选策略较多，所以能够实现利用交替分配启发式算法得到多层次配送中心连续选址的供应分配矩阵，其具体流程如下所示：

1)把m个供应零售商任意划分为l组，各组均存在一个负责满足零售商需求的配送中心，完成供应分配矩阵S的初步明确，矩阵表达式如下

S=(lij)m×l

(16)

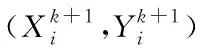
3)计算零售商j与配送中心i之间运输费用额，公式如下

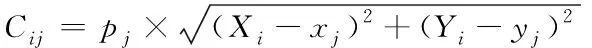
(17)

上式需满足解得结果为极小值，若结果非极小值，则需要对其进行调整，并依据调整后的结果，确定新的供应分配矩阵Sk=(lij)m×l；

4)重复以上步骤，直至将全部零售商都划分给运输费用总额最少的冷链物流多层级配送中心为止，此时得到的物流配送中心的最优选址策略，不仅所有配送中心地址均为最优选址，而且运输费用总额也是最少的。

4.2 基于时效性与安全性约束条件的模型计算

由于本文所构建的连续选址模型存在约束的非线性规划问题，因此在上述研究的基础上需要采用MATLAB软件内的fmincon(·)函数完成模型求解。fmincon(·)函数的调用格式如下所示

[x，fval]=fmincon(@fun，x0，A，b，Aeq，beq，

bl，ul，@con，@eon)

(18)

其中，输出的选址结果与目标函数值分别为x与fval，经过MATLAB语言编辑的目标函数文件、时效性约束文件以及安全性约束文件分别用fun、con和eon表示，配送中心坐标的上限、下限取值为bl和ul，A、b、Aeq和beq均表示空集，原始可行解为(x0，y0)，由于该可行解为最优策略查找的起点坐标，因此将其放置在配送范围的中心区域，并满足下式

x0=[min{xa1}+max{xa1}/2]

y0=[min{xa2}+max{xa2}/2]

(19)

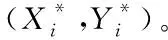
5 仿真研究

为了验证冷链物流多层级配送中心连续选址模型的有效性，进行了仿真。仿真环境如下：处理器是Intel(R) Core(TM) i5-2520M，内存为4GB，操作系统是Linux，模型性能分析选用的是MATLAB优化工具箱。

设定一级配送中心数量为4个，二级配送中心数量为10个，以售卖的海鲜产品作为配送货物，其运输温度要求是-3℃，平均售价是15元/kg。物流车辆的行驶平均速度25km/h，推算得出每公里的配送成本是0.2元/kg。表1与表2分别为选址模型的参数信息以及一级配送中心的成本与容量数据。

表1 选址模型参数信息

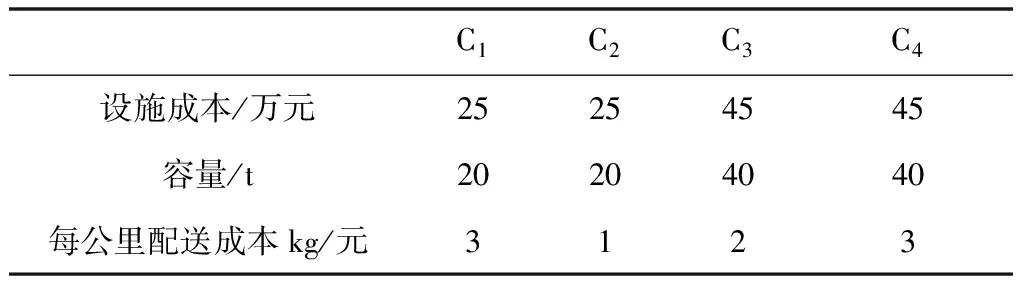
表2 一级配送中心的成本及容量信息

基于上表中的各项数据，比较文献[2]方法、文献[3]方法与研究方法的物流配送中心选址结果，结果如图2所示。

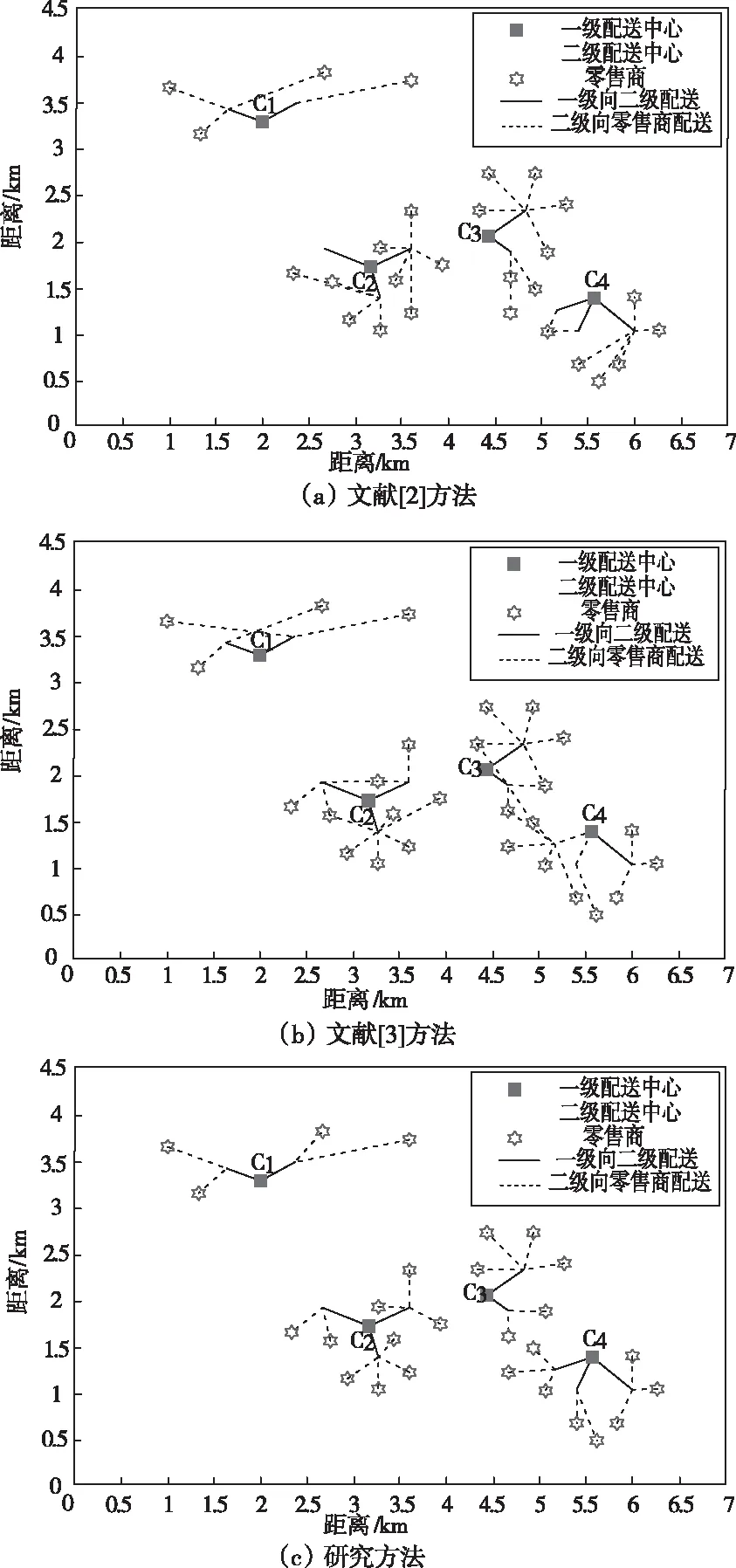
图2 不同方法选址结果比较

分析图2可知，文献[2]方法在一级配送中心C1的服务范围内，二级配送中心与零售商之间的路径规划并不合理，且在C4的服务范围内出现了多个二级配送中心为同一个零售商提供物流服务的情况，因此该方法的物流配送中心选址结果并不合理。文献[3]方法在一级配送中心C1的服务范围内，二级配送中心与零售商之间的路径规划也不合理，在其它一级配送中心的服务范围内，出现了路径规划混乱的情况，且多次出现多个二级配送中心为同一个零售商提供物流服务的问题，因此该方法的实际应用效果并不好。研究方法的物流配送路径设计合理，且无一次出现多个二级配送中心为同一个零售商提供物流服务的问题，因此该方法的选址结果最优，与文献方法相比，能够取得更好的应用效果。

在上述实验的基础上，进行算法迭代过程比较，实验结果如图3所示。

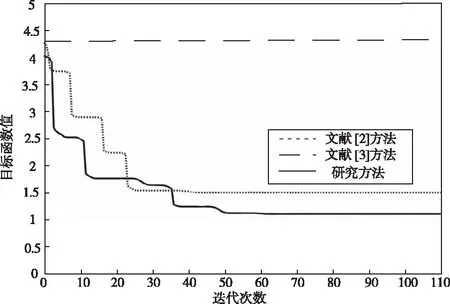
图3 算法迭代过程比较

分析上图可知，文献[3]所使用的算法始终未收敛，不能获得物流配送中心最优选址结果。文献[2]所使用的算法在迭代88次之后因陷入局部最优解而收敛。本文所使用的算法在初始化过程中，其目标函数值就优于文献[2]算法，且在文献[3]所使用的算法陷入局部最优之后，本文算法仍在继续寻优，在迭代113次后，得到冷链物流多层级配送中心连续选址的最优解。

6 结论

生鲜货物具有易腐坏的特点，选择正确的多层级配送中心地址对冷链物流供应链的整体发展具有至关重要的意义，又因配送中心建设较大，所以在选址时应提前做好全方位的预测，故提出冷链物流多层级配送中心连续选址建模方法。分析配送中心选址流程，构建费用最少与时长最短的两个目标函数及相应的约束条件，将选址问题转换为多源Weber问题，利用启发式算法对该问题进行求解，通过备选策略数，完成供应分配矩阵的构建。基于配送费用总额求解公式，对所得配送中心地址坐标进行多次判定与调整，实现选址模型构建及求解。实验结果显示，本文模型所得结果较为符合现实应用状况，应用效果好，为后续研究提供了重要的数据参考。