基于大数据的圆对称扩频数字图像篡改盲检测

李 兵，赵明华，王 锋

(西安理工大学计算机科学与工程学院，陕西 西安 710048)

1 引言

伴随大数据时代的来临，数字图像被广泛使用于人们的工作生活中，图像编辑与处理工具也得到迅猛发展，通过图像编辑工具可以伪造出真假难辨的数字图像，颠覆了人类“眼见为实”的传统观念[1]。尤其是将数字图像篡改应用在政治、军事及司法等敏感领域时，会对社会的平稳发展带来很多负面影响。由此可以看出，关于数字图像篡改检测的研究拥有重要意义[2]。

数字水印是通过数字嵌入的形式将信息隐藏在数字化媒体内，以此完成隐秘传输、身份验证、版权保护等功能，将此种手段应用于数字图像内，能够极大地维护图像的信息安全，具备极高的应用价值。文献[3]提出了基于SVD和直方图的JPEG同幅图像篡改盲检测方法，分析了基于小波变换和奇异值分解方法对同幅图像拼接篡改检测的缺点，结合相关重要的思想，构建了一种改进算法，该算法运用SVD提取图像块特征，并采用偏移频率的直方图来确定阈值。但是该方法的图像篡改盲检测精度较低。文献[4]提出了基于双信息统计与引力聚类的图像篡改检测方法，利用Hessian矩阵来准确提取图像的特征点，通过图像的梯度直方图来描述图像的方向特征，并联合图像的颜色信息，构造双信息统计机制，获取图像的特征向量，计算特征向量间的欧氏距离，构造近似测量模型，对图像特征进行匹配，利用引力聚类方法，实现图像特征点的聚类，精准检测复制-粘贴篡改内容。但是该方法的图像篡改盲检测时间较长，导致检测效率较低。

针对上述问题，本文提出一种基于大数据的圆对称扩频数字图像篡改盲检测方法。首先通过基于大数据的圆对称扩频数字图像水印算法，利用伪随机发生器得到一个圆形水印，将初始图像进行DFT转换，得到嵌入水印后的数字图像，并精准判断出图像是否被恶意篡改；其次建立图像篡改模型，识别图像来源，探测图像完整性，并对篡改方位实现有效定位；然后利用双重变换下数字图像篡改盲检测方法，以此检测图像的真实性；最后进行仿真，证明本文方法的适用性及检测精度和效率均优于传统方法，可在真实场景中进行广泛应用。

2 基于大数据的圆对称扩频数字图像水印算法

在大数据环境下，扩频通信是指通过伪随机码将被传输信号采取频谱扩展，让占据的信道带宽远远高于在一般通信状态下的最小带宽。圆对称扩频数字图像是将一圆对称水印嵌入到了图像的频域中，使用扩频通信技术输送一个窄带水印，以此达到不可感知性及鲁棒性统一的目的。

本文提出的水印算法是基于变换域方法，使用DFT特征在图像频域内嵌入一个圆对称扩频水印，可以准确判断出图像是否被篡改，能够有效保护数字图像的数据安全。

若初始图像是实型离散函数I(x，y)，0≤x≤N-1、0≤y≤N-1，且N=M，那么将此二维离散傅立叶转换表示为

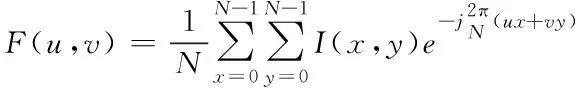
(1)

如果M、Φ是复数F(u，v)的振幅及相位，那么可得到

M=|F(u，v)|，Φ=∠F(u，v)

(2)

水印嵌入可划分为三部分。首先通过伪随机发生器生成一个圆形水印

(3)

式中，wi表示伪随机矢量w的第i个分量，R表示圆形水印半径。式(3)证明伪随机发生器陆续输出均位于以频域原点为中心的圆内，位于圆外的点赋值都是0[5]。

其次，将初始图像采取DFT变换，把W(u，v)引入初始图像傅氏频度的振幅内

Mw(u，v)=M(u，v)+αWc(u，v)

(4)

式中，α为按照经验挑选的视觉参数值，可以维护水印的透明度及鲁棒性。

最后，将Mw与Φ进行IDFT变换，获取嵌入水印后的数字图像Iw(x，y)。

检测水印不需要初始图像作为参照，仅需要把待测图像采取傅立叶逆向转换，然后从水印嵌入的位置进行水印提取，提取后的水印因为包含初始图像的频谱成分和恶意袭击，所以与原本水印拥有很大差别。此时要使用一个判断准则来断定是否参杂水印数据[6]。本文运用水印和原水印的关联性当作权衡标准，将其描述为

(5)

式中，W′与W依次为待判断水印和正确水印，Corr值的择取范围在[0，1]之间，若该关联值超出某个临界值，则断定该数字图像内拥有水印。

3 基于JPEG双重压缩效应的数字图像篡改模型

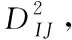
若JPEG压缩时的量化，采用四舍五入的取整手段，那么可得到

(6)

式中[·]为四舍五入取整，Q1为初始量化步长。

如果没有实现量化的系数是du，采取两次量化后的系数是D2，两次量化的步长依次为Q1、Q2，则

(7)

不论Q1是奇数还是偶数，只要没有量化的DCT系数du处在上面区间之中，那么双重压缩量化后获得的系数是D2，所以可利用区间长度构建数字图像篡改模型

(8)

现阶段，许多数字图像都是利用JPEG图像压缩标准进行储存，在JPEG图像的空域篡改处理后会再次进行JPEG压缩，将其保存为JPEG格式[7]。

将模型与双重压缩效应进行融合可以看出，若一张JPEG图像包括篡改与非篡改部分，则非篡改部分的DCT系数依旧具备双量化功效，此部分和初始JPEG图像双重压缩后的对照部分相同，篡改部分将不具备双压缩效果[8]。

通过构建数字图像篡改模型，可以有效鉴别图像的来源及完整性，并对图像被篡改位置进行精准定位。

4 基于双重变换的数字图像篡改盲检测

4.1 Radon变换及性质分析

假设一个二维函数f(x，y)的Radon变换为此函数平面中一组直线的线积分，将其描述为

P(r，θ)=R(r，θ){f(x，y)}

(9)

其中，|r|表示原点O与直线的间距，θ∈[0，π]表示直线和y轴之间的夹角，δ(r)为Dirac函数。

通过式(9)可知，Radon变换是把二维函数f(x，y)沿直线r-xcosθ-ysinθ=0实现积分，借此得到在随机(r，θ)位置上，f(x，y)沿该直线的求和值P(r，θ)。Radon变换针对数字图像的几何转换具有以下特质：

1)平移特质，可将平移过程描述为式(10)，式中r0=x0cosθ+y0sinθ0。

R(r，θ){f(x-x0，y-y0)}=P(r-r0，θ)

(10)

2)旋转特质，其中旋转角度是φ

R(r，θ){f(xcosφ+ysinφ，-xcosφ+ysinφ)}

=P(r，θ+φ)

(11)

3)尺度变换特质，其中尺度变换元素是λ，且λ≠0

(12)

此外，当f(x，y)为持续变化的状态时，每个点及每个方向噪声的Radon变换为一个常量，且该常量与噪声的平均值相同，均等于0，因此可以得到

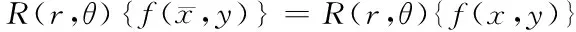
(13)

这就表示零均值的加性噪声对Radon变换后的数字图像不会发生影响[9]。

4.2 解析Fourier-Mellin变换

利用极坐标代表二维函数g(r，θ)的解析Fourier-Mellin变换，将其表达成

(14)

其中，s=σ-iu，u是一个实数参变量，σ是一个不小于0的实常数，通常取值为0.5。对P(r，θ)采取Fourier-Mellin变换，可将式(14)转换为

(15)

通过上式可知，利用Radon变换和Fourier-Mellin变换后，初始数字图像f(x，y)的旋转变换就转变成一个相位元素，初始图像的尺度变换就转变成一个幅度元素[10]。

在本文方法中，要预先将数组图像采取叠加分块处理，将整张图像根据范围像素位移分割成多个叠加块，块大小的设定不能高于篡改块。

如果图像大小是M*N，叠加块大小是R*R，那么分割的叠加块数量可描述为

S=(M-R+1)*(N-R+1)

(16)

因此，可将式(15)表示成

(17)

根据不变函数Z(u，k)所提取的图像，其旋转变换和尺度变换的不变特性为

(18)

(19)

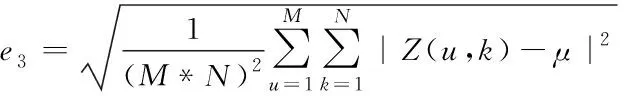
(20)

(21)

式中，μ表示函数Z(u，k)的平均值，M、N分别是Z(u，k)的行数和列数，这四个特性值可以检测出数据图像是否有旋转、缩放等篡改动作。由此，可以对图像内每个叠加块的四个特性值进行提取，将提取获得的三维特性矩阵描述

Bi，j(1：4)=[e1，e2，e3，e4]

(22)

复制粘贴篡改会使图像内包含两个相近块，通过计算每个叠加块提取的特性相近度，就能找出两个相近块在数字图像的区域位置。本文使用欧氏距离来推算出每个特性矢量的相近度大小。欧氏距离的推导解析式为

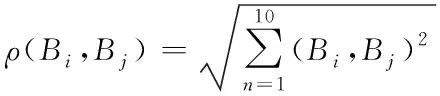
(23)

利用式(24)更深层地计算相近度大小

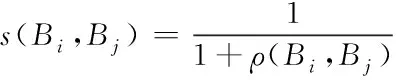
(24)

将设定阈值T和式(24)的计算结果进行对比，在s>T的情况下，表明图像内包含相近区域。

因为在数字图像中拥有诸多平坦区域，在篡改盲检测时极有可能发生虚警反应，所以判断结果一方面要设置一个适当的阈值T，另一方面还要使用主转移矢量算法去除错误块。此外，针对数字图像的划分，分块越大，检测效率就越好，在相同阈值T的基础上，误检的几率也就越高；反之，如果分块的划分太小，检测精度虽然较高，但降低了检测效率，同时虚警反应概率也相对很高。经过多次验证，本文将数字图像篡改盲检测的分块大小确定为8×8。

通过上述过程，可以进一步明确图像的真实性，并在大数据环境下对篡改区域的旋转平移等篡改状态进行精准检测。

5 仿真研究

为了验证本文所提基于大数据的圆对称扩频数字图像篡改盲检测方法的有效性，利用MATLAB平台，在Windows 10操作系统，处理器为AMD Athlon(tm)II P360 Dual-Core Processor 2.30 GHz，内存为24G，测试图像的帧率为30fps，分辨率为800*600的环境下进行仿真对比实验。图1为原始数字图像。

图1 原始数字图像

图像在进行合成类篡改时，篡改区域的大小、预想及初始图像压缩因子的差值都会对检测方法的精度造成较大影响。篡改图像如图2所示。

图2 篡改图像及区域

本文在上述实验环境下，将压缩因子的取值范围设定在0～100。将篡改区域面积占全部图像面积的百分比作为权衡篡改比例的原则。

图3为本文方法与文献[3]方法、文献[4]方法在不同篡改比例下不同压缩因子差值的检测精度。

图3 篡改盲检测精度对比结果

根据图3中的数据可知，伴随篡改比例的增多，文献[3]方法和文献[4]方法可以很清楚地看出权衡篡改区域及无篡改区域的不一致性，检测精度也逐步上升，但篡改盲检测精度最高只有13%和33%。而伴随篡改比例的增多，本文方法的检测精度呈现出先上升后下降的趋势，最高篡改盲检测精度为87%，这是因为本文方法是建构在图像DCT系数的统计特征内的，若篡改区域很小，统计特征不会发生显著变化，因此检测精度下降。综上所述，本文方法的篡改盲检测精度优于文献[3]方法和文献[4]方法的篡改盲检测精度。

为了进一步验证本文方法的有效性，对本文方法、文献[3]方法和文献[4]方法的数字图像篡改盲检测时间进行对比分析，对比结果如图4所示。

图4 图像篡改盲检测时间对比

根据图4可知，当迭代次数为5时，本文方法的数字图像篡改盲检测时间比文献[3]方法和文献[4]方法的数字图像篡改盲检测时间短，本文方法的数字图像篡改盲检测时间在142s内，而文献[3]方法和文献[4]方法的数字图像篡改盲检测时间均在160s内。说明本文方法的检测耗时较少，检测效率较高。

6 结论

为了提升数字图像篡改部分检测精度及效率，本文提出一种基于大数据的圆对称扩频数字图像篡改盲检测方法。通过将特征标识嵌入数字图像内，保护图像数据安全，利用基于JPEG双重压缩效应的数字图像篡改模型，检测图像完整度，对篡改位置实施精确定位；运用Radon变换及解析Fourier-Mellin变换明确图像的真实度。通过仿真，验证本文方法检测精度及效率均优于传统方法，具备较高的优越性。