一种均匀抗噪自适应的ORB特征提取算法

赵宇琦，连晓峰，谭 励，刘 栋

(1. 北京工商大学人工智能学院，北京 100048；2. 北京工商大学计算机学院，北京 100048)

1 引言

计算机视觉是近年来人工智能领域的研究热点，在自主驾驶、智慧城市、医疗诊断等许多领域得到广泛应用。研究内容主要包括图像分割[1]、目标检测与识别[2]、动态目标跟踪[3]等，其中图像特征提取算法的可靠性是保证这些后续研究的重要前提条件。自从1977年开始，现已提出各种特征提取算法。

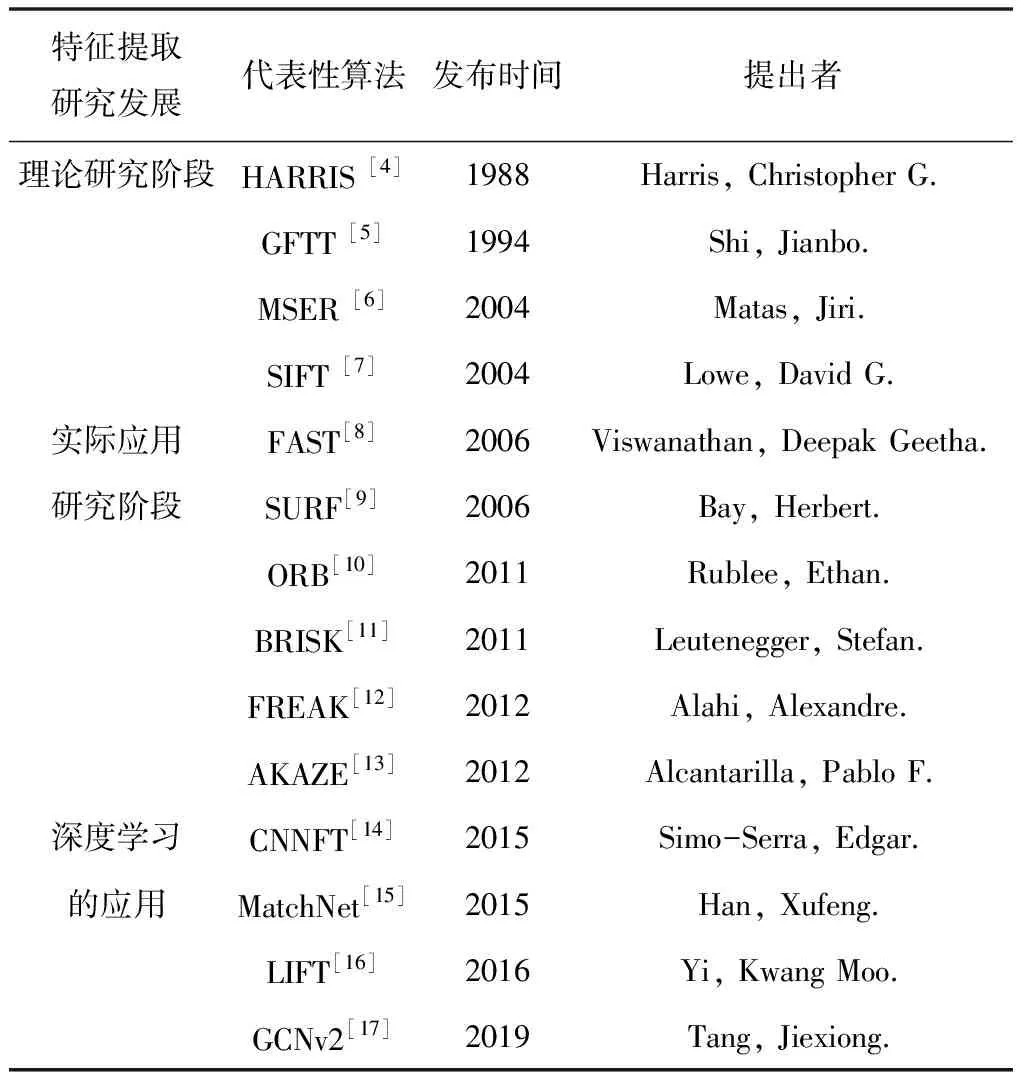
表1 特征提取算法发展

由表1可知，最早提出的Harris角点检测、MSER、GFTT等算法，主要是用于提取图像中的角点，尤其是2004年提出的SIFT算法因具有高精确度的特点而得到广泛应用，但由于其计算量过大，实际应用中的实时性较差。随后，研究人员着重于改进算法效率，以更好地应用于实际。于2006年提出的SURF算法是在SIFT算法的特征点检测速度方面进行了改进，但算法仍不尽如人意；FAST算法则是另辟蹊径提出的新算法，其优点是特征点检测速度快；于2011年，Rublee Ethan将FAST特征提取与BRIEF[18]特征描述相结合，提出了ORB特征检测算法，此算法在运算效率上优于SURF算法至少两个数量级，且具有较高的精度，已被多次应用在ORB-SLAM系统[19]中；BRISK、AKAZE、FREAK等算法借鉴了ORB算法的设计思路，并加以改进，分别增强了鲁棒性与精确度；由于深度学习的算法发展，研究人员开始将其与特征点检测相结合，并提出了LIFT，GCNv2等算法，受限于数据量的原因这些算法还未能应用于实际中。原始ORB算法对比像素点的灰度强度完成特征点的检测与描述，因此在缩放，旋转和噪声等情况下，鲁棒性有所下降。但由于原始ORB算法在上述算法中兼顾了实时性与计算精度，所以在充分研究原始ORB算法的基础上，结合图像金字塔[20]，灰度质心法[21]与图像四叉树理论[22]，提出了一种均匀抗噪自适应的ORB图像特征检测算法，首先采用快速自适应图像金字塔结构强化尺度自适应性能，并约束特征点数量，提高运算速度；其次提出三维描述子灰度质心法将算法的描述子从一维扩展到三维，在增强抗噪能力同时强化旋转自适应性能。最后采用四叉树特征管理算法进行优化，减少冗余特征点，增强鲁棒性，提高分布均匀度。

2 改进ORB算法

原始ORB算法主要包括特征点检测的FAST算法和特征点描述的BRIEF算法。

1)FAST的基本原理：设p点为待检测像素点(灰度值记为Ip)，以p点为圆心，选取周围16个像素点(如图1所示)，根据式(1)进行特征点判别：

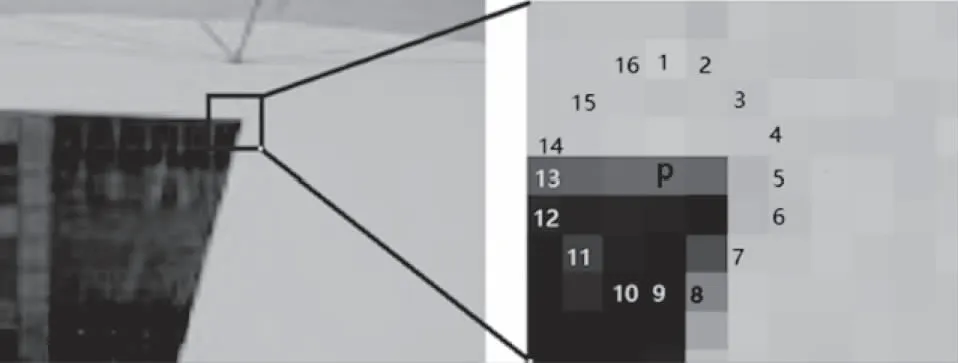
图1 FAST特征提取

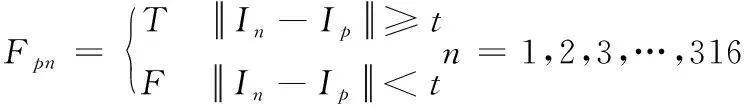
(1)

其中In为16个像素点中第n个像素点的灰度值；t为预先设定的阈值。若连续9个Fpn为T，则认为p是一个特征点。

2)BRIEF算法基本原理：设p点为特征点，以p点为中心选取31×31像素的邻域，随机选取256组像素点对(u，v)(记点u和点v的灰度值分别为I(u)与I(v))，根据式(2)进行特征点描述

(2)

BRIEF算法比较256组点对的灰度值，并根据τ生成256位的二进制数作为特征点的描述。

改进ORB算法对图像进行降采样处理，然后进行高斯滤波，其次进行差分运算，形成多尺度的图像金字塔，然后由FAST算法进行特征点检测，并由四叉树特征管理算法优化特征点，最后计算三维描述子灰度质心法完成特征点提取。改进算法如图2所示。

2.1 快速自适应图像金字塔——FAIP算法

针对原始ORB算法尺度自适应性较差的问题，在此提出一种改进的图像金字塔结构——FAIP算法来增强尺度自适应性，并提高算法运行效率。具体实现流程如图3所示：

首先对原图像进行高斯滤波

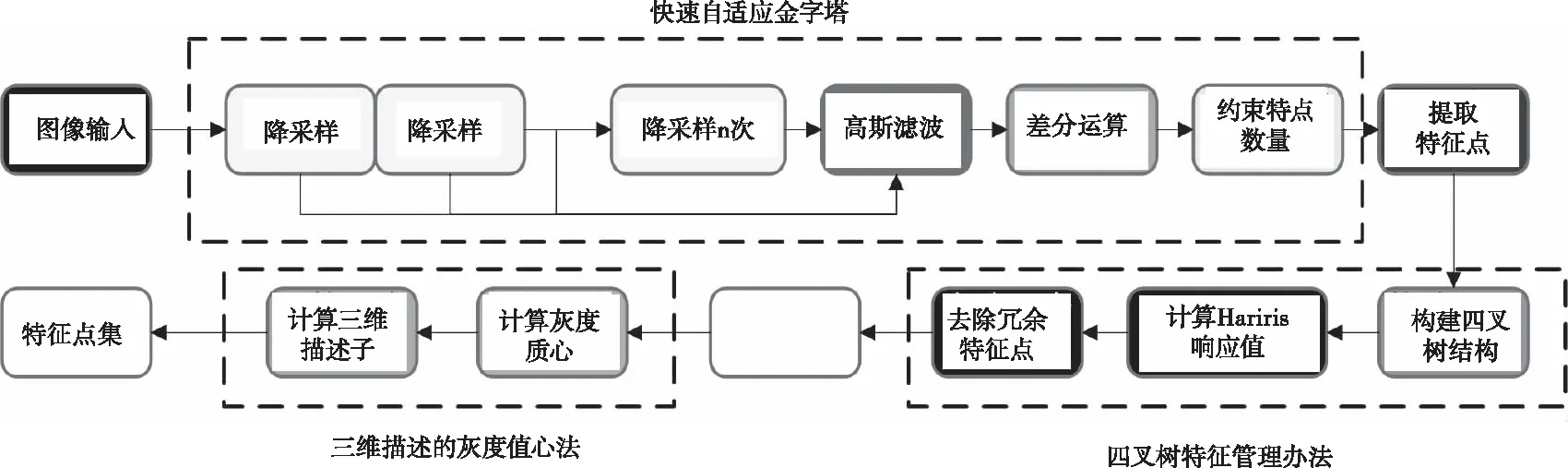
图2 算法实现框图

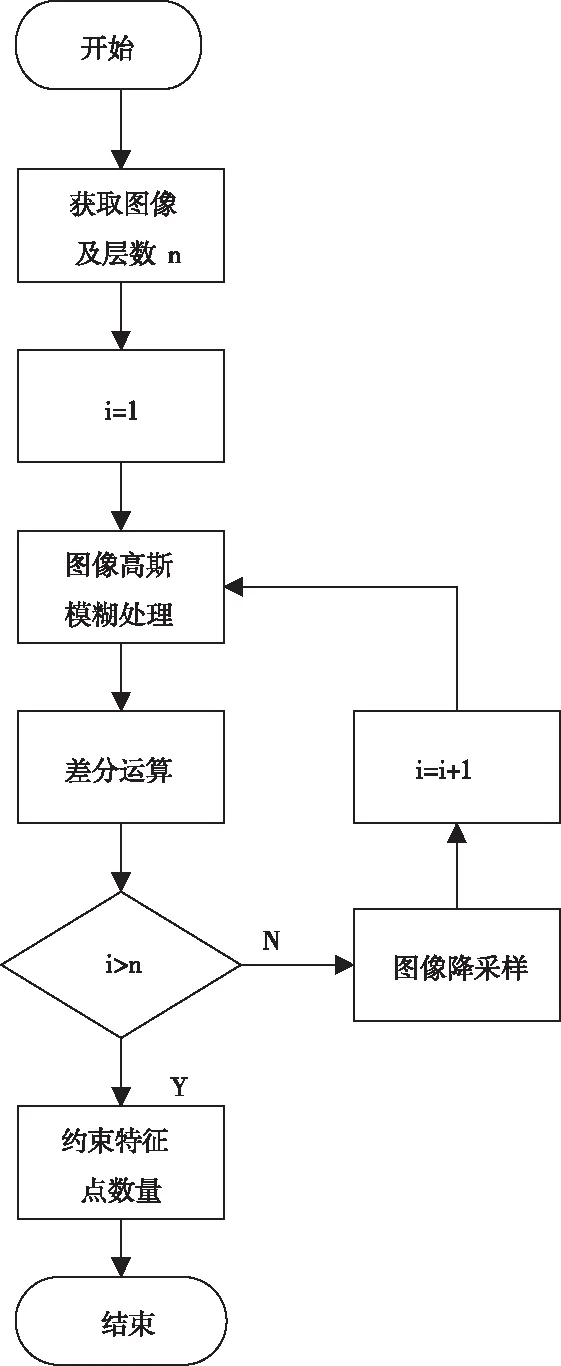
图3 快速自适应图像金字塔流程图

(3)

其中(x0-y0)为待滤波像素点坐标，(x，y)为滤波半径内所包含的像素点坐标，σ为滤波系数。其次将滤波后图像与原图像进行差分运算得到差分图像，并将差分图像进行归一化处理；然后按设定的缩放比例因子SC对原图像降采样N次，并逐层进行高斯滤波、差分运算、图像归一化步骤，最后得到差分图像构成的多尺度图像金字塔。另外，为提高运算效率，对N个尺度图像中可提取的特征点数量进行如下条件约束

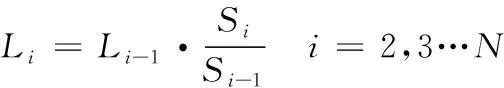
(4)

其中Li为第i层的特征点数量，Li-1为第i-1层的特征点数量，Si，Si-1分别为第i层和第i-1层的尺度。在此，引入杨氏算法[23]进行预选特征点检测，提升运算效率：

图4 杨氏算法示意图

设p点为待检测像素点，检测如图4所示4个像素点位，若有相邻两点Fpn=T，则p点为候选特征点，最后通过FAST算法筛选候选特征点中的FAST特征点。

2.2 三维描述子灰度质心法——3D-DGC

针对原始ORB算法旋转自适应性能差，抗噪能力弱，在此提出一种三维描述子灰度质心法——3D-DGC来解决上述问题。在以特征点p为中心的BRIEF图像块B中，建立以p点为原点的坐标系(如图5所示)，定义图像矩

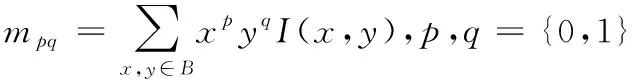
(5)

记点(x，y)的灰度值为I(x，y)。然后通过所得图像矩计算BRIEF图像块质心C(如图5白色像素点所示)

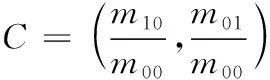
(6)

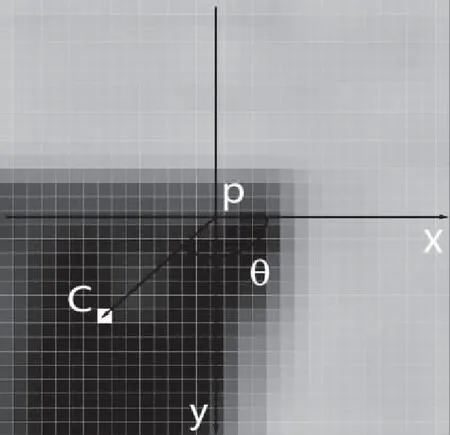
图5 灰度质心示意图

(7)

图6 灰度质心示意图((a)；(b))

因像素块灰度梯度值对噪声具有抗性，在此加入像素块在x轴与y轴正向方向上的灰度梯度值dx与dy作为改进描述，并定义操作α：

图7 四叉树优化方法示意图

(8)

则三维描述子向量为：

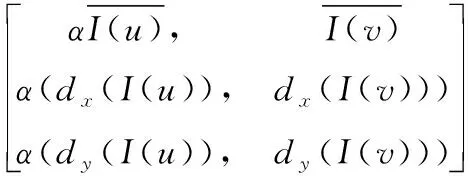
(9)

将128组点对(u，v)的坐标定义为2×256的矩阵D：

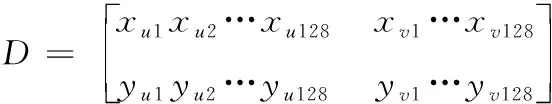
(10)

上式中x和y为点对(u，v)的坐标，然后以θ构建旋转矩阵对D旋转：

(11)

最后得到旋转自适应性能与抗噪能力较强的三维描述子灰度值心法。

2.3 四叉树特征管理算法——QtFM

针对原始ORB算法检测特征点密集度高，均匀性差的问题，将FAST算法的固定阈值改进为动态阈值，并提出四叉树特征管理算法——QtFM改进特征点均匀性。具体算法如下，首先根据I(n)与I(p)计算动态阈值：

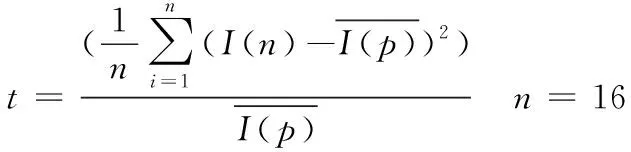
(12)

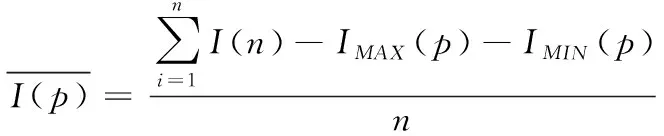
(13)

为提升特征点分布均匀度，首先对图像进行网格划分提取特征点，设定初始网格边长为a，然后根据图像分辨率对网格进行调整，计算出实际的分割行数与列数。以计算分割网格的宽为例，若图像的宽为W，则实际网格宽ω为

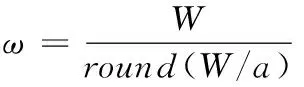
(14)

其中round为对结果取整。

网格划分完成后对每个网格中采用式(12)所得阈值检测特征点，若有网格未检测到特征点，则降低阈值t为原来的1/4再次进行提取，直到所有网格中都有特征点。

然后采用四叉树方法优化特征点分布均匀度。设特征点分布如图7(a)所示，四叉树方法先将图像均分为4个图像块(如图7(b)所示)，并定义为根节点，然后统计每个节点中特征点的数量，若数量大于1，则向下分裂子节点(如图7(c)所示)，如果等于1或已分裂4次则不再分裂，若特征点数量为零则舍弃节点(如图7(d)所示)；然后在每一个特征点数量大于1的节点内保留Harris响应[4]最好的特征点，如图7(e)所示，由此得到更加均匀的特征点分布。四叉树特征管理算法流程如图8所示：

图8 四叉树优化方法流程图

3 实验结果与分析

3.1 实验素材准备

3.1.1 实验平台

实验基于Ubuntu18.04 LTS操作系统进行，计算机CPU为i7-6700HQ，内存为8GB，所用OpenCV[24]版本为3.4.1。

3.1.2 实验数据

实验采用多个不同场景进行，共搜集了2547张图像构成测试数据集，包含机场、卧室、书店、办公室、仓库、地铁等24种不同场景，实验随机选取6组进行，并以平均值作为实验结果。

3.2 特征提取对比实验

3.2.1 特征提取均匀度对比

为了量化均匀度，采用了文献[25]提出的量化方法。从竖直、水平、45°和135°等4个方向以及中心和外围对图像进行区域划分，得到10个区域；计算出落在每个区域内的特征点数量，并根据这些数据计算出方差V，最后计算均匀度u

u=101log(V)

(15)

该数值越小，则不同区域内的特征点数量差别越小，分布均匀度越好。实验采用具有代表性的BRISK算法，ORB算法，SURF算法，以及文献[23]所提杨氏ORB算法进行对比

图9 不同算法对图片特征提取结果

其中图9(c) 改进ORB(Qoff)是将改进ORB算法的四叉树特征管理算法离线后的对比试验。原始ORB算法与BRISK算法检测特征点集中在纹理丰富的区域，针对弱纹理区域(如：地面，墙壁等)均未检测到特征点；杨氏ORB算法与SURF算法的均匀度优于BRISK与原始ORB算法，但存在特征点密集区域；改进ORB算法在纹理丰富区域未出现特征点密集现象，同时在弱纹理区域能检测到一定数量的特征点，有效提高了特征点分布均匀度。实验结果见表2。

表2 算法均匀度

表2呈现了整体的实验情况，较原始ORB算法而言对特征点的分布均匀度提升在10%以上。实验结果证明，改进ORB算法针对特征点分布均匀度具有较大的提升。表3为不同算法提取特征点所需时间的统计。

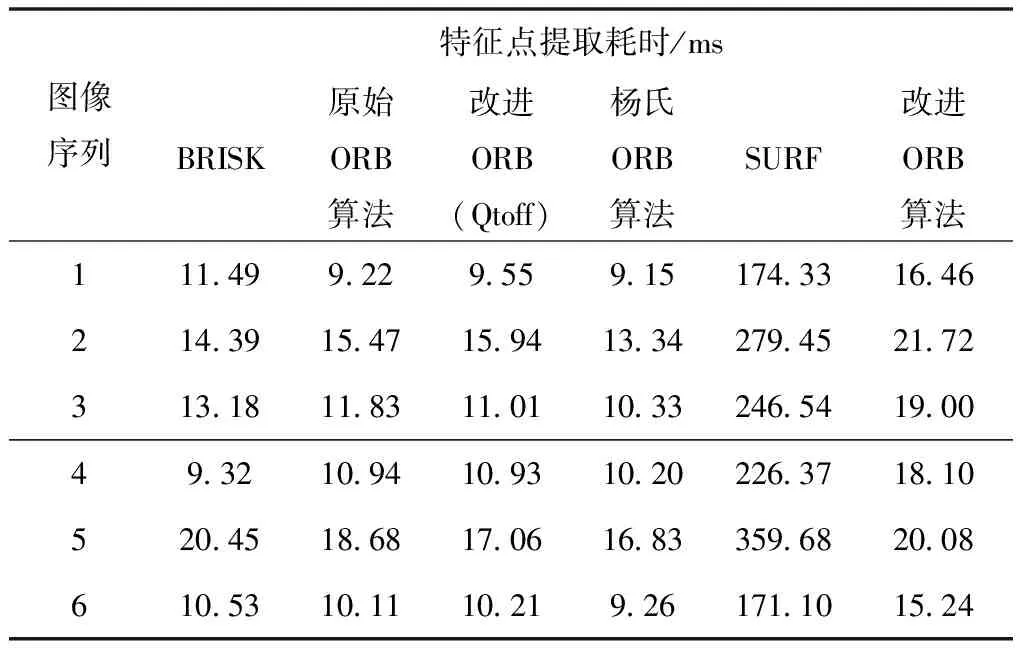
表3 算法效率

由表3可以看出，改进ORB算法继承原始ORB算法高效计算的特点，计算效率远远高于SURF算法。其计算效率有所降低，但在可接受范围内。

3.3 特征描述对比试验

3.3.1 特征描述自适应性能对比

为了验证本算法的尺度与旋转自适应性能，对每张图像降采样后旋转90度，然后与原图像进行特征匹配，并使用汉明距离优化匹配结果。结果如图10所示。

图10 不同算法的旋转与尺度的适应性

线段为特征点匹配线，代表匹配到的同一特征点的对应关系，其中改进ORB(P&GCoff)为将快速自适应图像金字塔和三维描述子灰度质心法离线后的改进ORB算法。从图10可以直观看出改进ORB算法相较于其它算法在图像存在旋转与缩放时能成功匹配更多的特征点。

表4 算法自适应性能

表4为各组配对特征点数量的均值。从表4可以更客观的看出，改进ORB算法拥有更好的旋转与尺度自适应性能。

3.3.2 特征描述抗噪能力对比

为了验证改进ORB算法在抗噪能力上的提升，对图片添加高斯噪声后提取特征点并进行暴力匹配结果如图11所示。

图11 不同算法对噪声的敏感度

从图11可以看出，改进ORB算法对噪声的敏感度要低于其它算法，成功配对特征点数量明显高于其它算法。

综上所述改进ORB算法在各种情况下均能保持较为优秀的分布均匀度，同时拥有良好的旋转与尺度自适应性能，并具有较好的抗噪能力。

4 结束语

改进ORB算法针对原始 ORB 算法特征点检测密集度高、抗噪能力弱、自适应性能差等问题，在原始ORB算法的基础上采用快速自适应图像金字塔，三维描述子质心法与四叉树特征管理算法等方法进行改进，应用大量不同场景的数据进行试验验证。实验结果表明，改进ORB算法提高了分布均匀度，增强了抗噪能力，强化了自适应性能，对解决实际问题具有一定的应用价值。