相位优化的压电纳米定位系统GADRC

赵峙尧，张念东，魏 伟

(1. 北京工商大学人工智能学院，北京 100048；2. 北京邮电大学自动化学院，北京 100876)

1 引言

纳米定位技术是对100nm甚至更小量级的认知和操控的技术[1]，纳米定位技术作为纳米制造技术的重要组成部分，是纳米测量、纳米加工的核心技术之一。压电陶瓷驱动器驱动力大、刚度高、重复性好， 适合作为纳米定位平台的驱动器[2]。这种机构已广泛应用于微操纵器，半导体制造行业[3，4]，超精密机床[5]。然而，压电陶瓷存在蠕变、迟滞非线性和微阻尼共振特性，对环境温度变化敏感[2]，使得此类系统的建模和控制具有挑战性。迟滞作为压电陶瓷固有的一种复杂非线性，对精度控制的影响最大。前馈控制技术是抑制迟滞的常用方法，通过串联迟滞补偿器降低迟滞的影响。基于Prandtl-Ishlinskii模型[6]、改进的Bouc-Wen模型[7]，建立迟滞逆模型，设计前馈控制，如基于改进的Bouc-Wen模型的前馈补偿方法[7]以及基于自适应的逆模型前馈补偿[8]。这些方法对迟滞模型有一定的依赖。不依赖迟滞模型的闭环控制将迟滞视为一种扰动，消除其影响。基于扰动观测的PID 控制[9]，重复控制[10，11]，time-delay control[12]，模型参考自适应控制[13]实现了具有一定鲁棒性的定位控制。更进一步，采用迟滞补偿的闭环复合控制也得到了应用。如：基于直接逆迟滞补偿的迭代学习控制[14]，基于逆补偿的模型参考自适应控制[15]。无论是基于迟滞模型前馈控制还是基于迟滞模型的闭环控制，都需要精确的迟滞模型。而不依赖迟滞模型的闭环控制则更为实用。

基于主动抗扰的控制思路，文献[16]将非线性特性视为总扰动的一部分，设计线性自抗扰控制(Linear active disturbance rejection control， LADRC)实现了具有较强鲁棒性的定位。LADRC只依赖于模型的相对阶和控制增益，这是该方法的优点，也是缺点。减小总扰动观测负担或提高观测能力可提升LADRC的控制性能。文献[17]提出了基于被控对象模型信息的广义自抗扰控制(Generalized Active Disturbance Rejection Control，GADRC)。将微位移台线性动力学模型用于控制器设计，是提高定位性能的常用方法[10-12]。在线性动力学模型的基础上设计GADRC控制器，广义扩张状态观测器(Generalized Extended State Observer， GESO)只需要观测未准确建模的线性部分和非线性部分，大大减轻了扰动估计负担。在提高观测器的性能方面，文献[18]提出相位优化的线性自抗扰控制(Phase Optimized LADRC，POLADRC)，利用微分信号的相位超前性，优化观测器，在压电纳米定位台上测试取得了比LADRC更好的定位性能。应用相位优化的思路进一步提高GADRC的控制能力，从而实现在减轻扰动估计负担的同时，提高扰动估计能力。

LADRC与PID控制有着内在的联系，文献[19]将二阶LADRC等效为反馈补偿器结合滤波器的结构。在此基础上，文献[20]将二阶LADRC等效为二阶低通滤波器串联理想PID控制器的结构。同时，无论LADRC还是GADRC，在等效为内模控制回路时，等效的内部模型都是构建扩张状态观测器的基准模型，通过内模控制可以证明GADRC的稳定性[21，22]。本文从参考模型的角度解释扩张状态观测器，不同于模型参考控制以一个参考模型的输出为样板让实际控制对象向其接近，直至一致。扩张状态观测器是通过一个理想PID使得参考模型跟随实际对象输出，理想PID控制量的一部分作为总扰动的估计结果，两者在工作原理上有根本不同。通过模型参考的解释思路，进一步理解POLADRC的同时，也获得相位优化规律在GADRC中应用的参数整定方法，提出相位优化的广义自抗扰控制(Phase Optimized GADRC，POGADRC)

2 实验台参数及其线性模型

图1显示了不同频率电压输入时的迟滞回线。理想情况下，没有迟滞特性的回线为45°的直线。

表1 纳米定位实验系统参数表

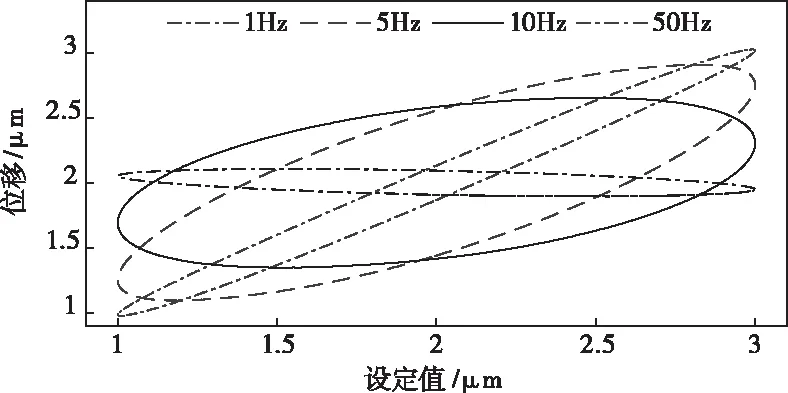
图1 不同频率的迟滞回线

文献[11]通过施加1 Hz至 250Hz的低振幅正弦电压扫描信号，辨识压电纳米定位平台的线性动力学模型。较低振幅电压激励，避免了迟滞非线性引起的失真。采用正弦扫描信号0.1sin(50πt2)，0≤t≤10，建立线性模型Pm1(s)和Pm2(s)。已建立模型和纳米定位台实际的频率响应如图2所示，Pm1(s)和Pm2(s)准确地描述了系统较低频率范围内的动力学特性，Pm2(s)在较高频率部分也具有较高的准确性。Pm2(s)显示实验台的实际谐振频率约为225Hz。

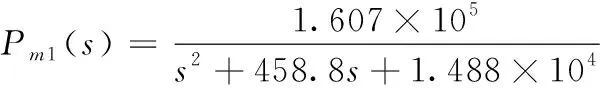
(1)

Pm2(s)=

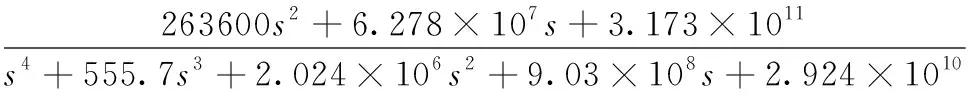
(2)

图2 识别模型和测量值的频率响应

3 相位优化的广义自抗扰控制

不同于LADRC只需要关键参数：被控对象的阶次和控制量增益b0，GADRC可以利用更多的模型信息。考虑到控制器的复杂程度，选择阶次较低的模型Pm1(s)作为基准模型，二阶模型Pm1(s)在较低频率范围内与实验台实际模型符合度较高，能够满足在较低频率范围内定位控制的要求。

3.1 线性自抗扰控制

参考文献[23]设计二阶LADRC控制器，如图3所示。其核心部分线性扩张状态观测器(Linear Extended State Observer， LESO)为

(3)

z1，z2为状态观测，z3为总扰动估计，y为被控对象输出。LADRC控制律

(4)

采用带宽整定参数法[23]

3.2 广义自抗扰控制

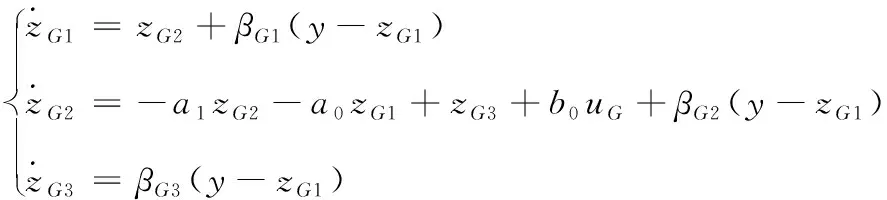
(5)

zG1，zG2，zG3为GESO的输出，y为被控对象输出。GADRC控制律

(6)

采用带宽整定参数法[17]

(7)

ωo，ωc为GESO观测带宽和控制器带宽。

3.3 相位优化的线性自抗扰控制

(8)

POLADRC控制律

(9)

z1，z2为状态观测，zpo3为相位优化之后得总扰动估计。可调参数c=β2/β3。

zpo3=z3+β2(yp-z1)

(10)

由式(3)和(10)，相对于LESO，在总扰动估计中，增加的一项是(y-z1)β2。

在相位优化律的作用下，POESO的估计相位总是超前于LESO。相位超前使得观测器估计速度更快、估计误差更小。文献[9]分析结果显示，当总扰动是阶跃形式时，POESO和LESO对总扰动估计的稳态误差都为0，当总扰动是斜坡形式时，POESO对总扰动估计的稳态误差都为0，而LESO对总扰动估计存在稳态误差。本文将应用POLADRC的改进思路提高GADRC控制效果。

3.4 扩张状态观测器的参考模型解释

在二阶LADRC中，LESO以b0/s2为基准模型，理想情况下， LESO通过总扰动补偿，将被控对象转换为串联积分的形式。

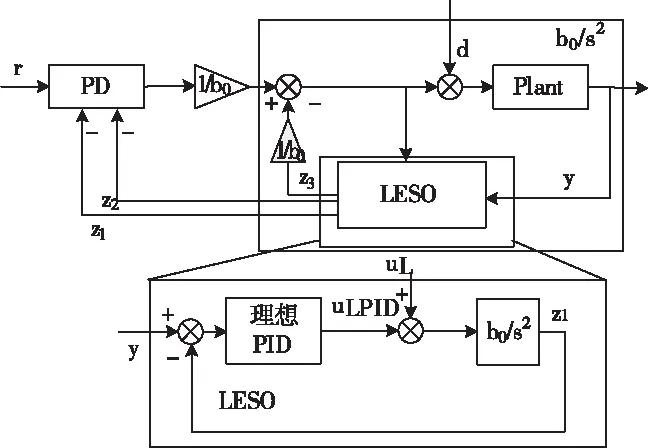
图3 二阶LADRC控制框图

结合图3，式(3)可以整理为：

(10)

其中：

(11)

z1是参考模型b0/s2的输出，通过一个理想的PID控制器，实现参考模型输出z1对被控对象输出y的跟踪。结合图3和式(4)，(11)，总扰动补偿回路中的补偿项为z3/b0，是LESO中等效理想PID中的积分项。

同理，结合图4和式(6)，GESO以Pm(s)为基准模型，理想情况下，在补偿项zG3/b0作用下，补偿回路的输入输出之间的动态特性与基准模型Pm(s) 动态特性相同。

图4 二阶GADRC控制框图

式(5)可整理为：

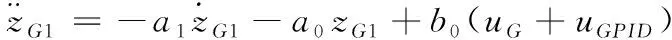
(12)

其中

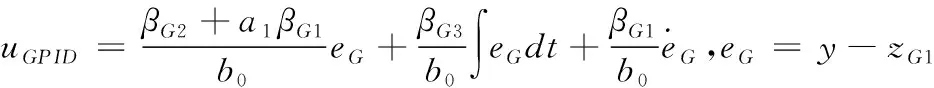
(13)

zG1是参考模型Pm(s)的输出。通过一个理想的PID控制器，zG1实现对被控对象输出y跟踪。由图4和式(6)，(13)可知，补偿项zG3/b0是GESO中等效理想PID中的积分项。

从参考模型的角度出发，LESO和GESO的内部工作原理是通过一个理想的PID控制器，实现参考模型对实际对象的跟踪。

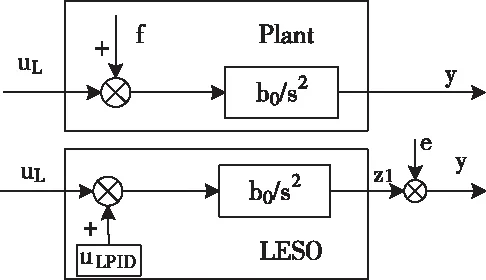
图5 LESO和实际对象的等效框图

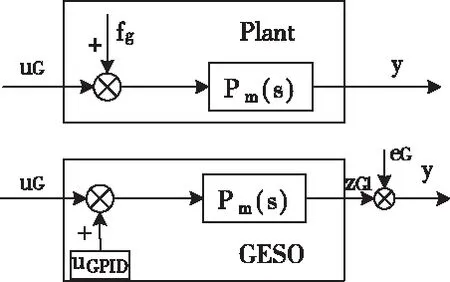
图6 GESO和实际对象的等效框图

3.5 相位优化的广义自抗扰控制

将相位优化规律应用到GADRC中，控制律中的扰动补偿项为积分加比例的形式。由式(5)和(13)，相位优化的GESO为

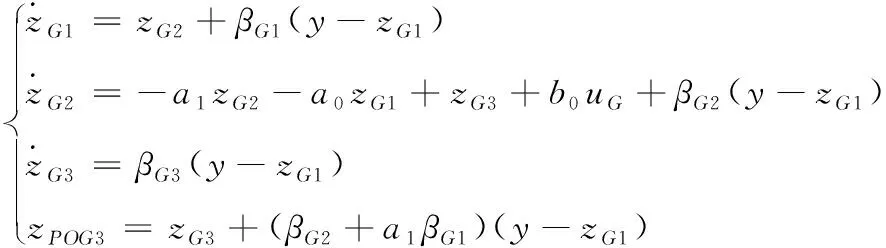
(14)

POGADRC控制律

(15)

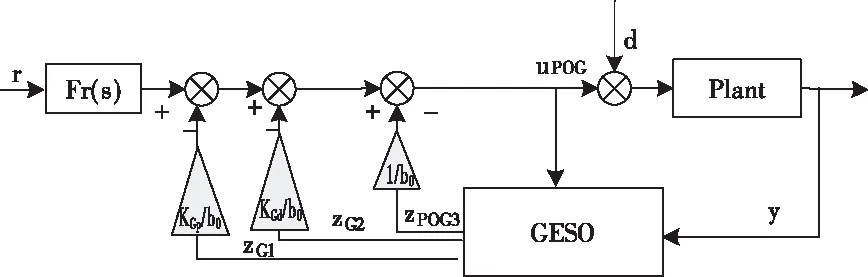
图7 POGADRC控制框图

4 纳米定位实验台实验对比

实验在P-561.3CD上进行，压电驱动器与电压放大器E-727.3CDA连接。采样间隔设置为0.05 ms。实验平台如图9。以阶跃信号和正弦信号作为参考信号，进行多项实验。POGADRC，GADRC和 LADRC控制器参数见表2。

图8 纳米定位实验平台

表2 POGADRC，GADRC和 LADRC控制器参数

4.1 阶跃跟踪实验

图9 阶跃跟踪实验

响应结果如图9， POGADRC阶跃设定值的响应曲线更加平滑，收敛更快。当定位台受到阶跃或正弦外部电压扰动时，POGADRC受到的影响更小。

4.2 正弦跟踪实验

本节中，POGADRC的优势通过跟踪时变参考信号的响应来证明，实验中1Hz、5Hz、10Hz和50Hz正弦信号作为设定值。 其中，5Hz正弦跟踪实验Ⅰ中，r(t)=sin(10πt)+3，不施加外部扰动。5Hz正弦跟踪实验Ⅱ中，r(t)=sin(10πt)+3，施加外部电压扰动：d2(t)=-0.1ε(t-1)-0.1ε(t-4)sin(2πt)。实验结果如图10，11，12，13所示。

图10 5Hz正弦跟踪实验Ⅰ

图11 5Hz正弦跟踪实验Ⅰ跟随偏差

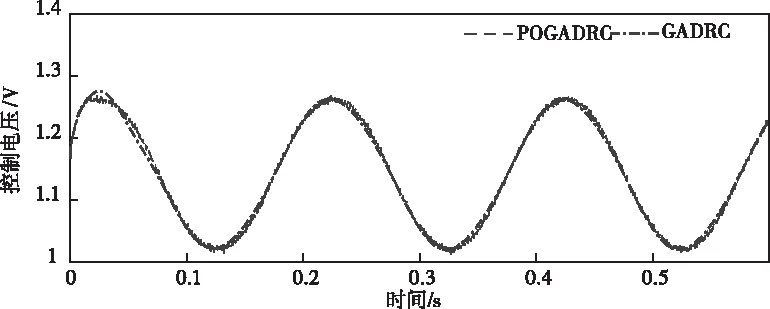
图12 5Hz正弦跟踪实验Ⅰ控制量

图13 5Hz正弦跟踪实验Ⅱ

以跟踪误差的均方根误差(Root Mean Square of Error， RMSE)和控制信号u的均方根误差(Root Mean Square of u， RMSU)作为定量比较的对比项，RMSU表征控制量的能量。相对变化量表示POGADRC相对GADRC， RMSE或RMSE的相对变化量。对于RMSE而言，相对变化量为负值时，表示跟踪误差相对变小，控制效果提高，反之则控制能力未提高或降低。对于RMSE而言，相对变化量为负值时，表示跟踪消耗的能量减少，反之消耗的能量不变或增加。表3反应了不同频率下，无外部电压扰动跟随实验在三个正弦周期内的RMSE和RMSU数据。在RMSU几乎相同的情况下，POGADRC控制偏差更小。

表3 未施加外部电压扰动的正弦跟随响应结果RMSE和RMSU定量比较

图14显示了在GADRC和POGADRC闭环控制下和开环条件下实验台的迟滞回线。GADRC和POGADRC都表现出了较好的迟滞非线性抑制能力。跟随频率为50Hz时，两者抑制效果相近，跟随频率较低时，1 Hz、5 Hz、10 Hz条件下，POGADRC表现出优于GADRC的非线性抑制能力。

图14 开环和闭环控制下迟滞回线对比

5 结论

为实现对具由迟滞非线性特性压电驱动的纳米定位台良好的定位控制，在建立的实验台线性模型的基础上，设计了POGADRC。实验结果表明，POGADRC具有更优的动态响应特性和扰动、迟滞非线性抑制能力，实现了压电驱动的纳米定位台的良好定位控制，这为自抗扰控制在压电驱动的纳米定位领域的应用提供了一种实用控制方案。