碳族元素原子簇分子结构稳定性的仿真

马丹丹，秦湘阁

(1. 佳木斯大学信息电子技术学院，黑龙江 佳木斯 154007；2. 佳木斯大学材料科学与工程学院，黑龙江 佳木斯 154007)

1 引言

碳原子簇属于多炔链状结构，具有多重键性质[1]。对于质量较小的原子簇来说，上述结构是合理的，但需要在原子簇两端连接氮原子或氢原子，才能够使其稳定。需N原子和H原子连接且质量较大的碳原子簇的结构不是链状的，假定原子簇的结构为金刚石或石墨结构，则附近或表面的碳原子价态无法达到饱和状态，且稳定性较低[2]。通过上述分析可知，碳族元素原子簇具有全新的结构特点，属于碳的同素异构体，因此需要对碳族元素原子簇分子的结构稳定性进行分析。

乔建刚[3]等人提出基于粗糙集赋权的簇分子结构稳定性分析方法，该方法根据碳族元素原子簇分子结构的特点，选取稳定性评价指标，并对其进行定量和定性处理，在指标量化标准的基础上对指标进行离散化处理，将分子结构稳定性分为四个等级，通过粗糙集理论对指标对应的权重进行计算，根据可拓学理论构建分子结构稳定性评价模型，实现分子结构稳定性的分析，该方法没有分析分子结构稳定性与影响因素之间存在的关系，得到的分析结果与实际不符。王佳信[4]等人提出基于因子分析的分子结构稳定性分析方法，该方法通过因子分析方法降维处理稳定性相关指标数据，采用概率神经网络利用处理后的数据构建结构稳定性评价模型，实现分子结构稳定性的分析，该方法选取指标时没有考虑结构稳定性与影响因素的关系，导致分析结果的相对误差较大。

为了解决上述方法中存在的问题，提出碳族元素原子簇分子结构稳定性的仿真方法。

2 分子结构稳定性评价指标

碳族元素原子簇分子结构稳定性的仿真方法结合支持向量回归法和粒子群算法对分子结构稳定性与影响因素之间存在的关系进行分析，选取碳族元素原子簇分子结构稳定性评价指标。

2.1 影响因素分析

SVR模型的泛化能力和学习精度通常情况下会受到σ、C、ε的影响，其中，σ代表的是核函数参数、C代表的是惩罚因子、ε代表的是不敏感损失系数。

控制函数拟合误差与样本噪声之前存在密切的关系。支持向量的数量随着不敏感损失系数ε的增大而减少，降低了模型的复杂性，同时也降低了回归精度。回归精度随着不敏感损失系数ε的减小而增大，模型的复杂性较高，此时支持向量数量有所增加[5]。

核参数σ描述了支持向量间的相关性，核参数σ与支持向量间的相关性呈正比关系，当核参数σ的值越大时，相关性越强，当核参数σ的值越小时，相关性越弱[6]。

所提方法通过粒子群算法优化选取SVR参数提高SVR泛化性能。设(C，σ)代表的是SVR参数，可以对粒子进行描述。优化过程中的适应度函数fMAPE选取平均绝对百分比误差

(1)

碳族元素原子簇分子结构稳定性的仿真方法分析分子结构稳定性与影响因素关系的具体步骤如下：

1)输入分子结构的样本集。

2)粒子通过随机初始化处理后构成粒子群体，并生成初始速度；粒子个体极值pbest通常情况下与其当前位置相对应，根据粒子适应度值对粒子和粒子群搜索到的最优位置pi=(pi1，pi2，…，piD)、pg=(pg1，pg2，…，pgD) 进行更新[6]。

3)比较全局极值gbest和粒子更新后的pbest，确定保留原始或对极值gbest进行更新。

4)通过下述公式对粒子对应的位置和速度进行更新

(2)

式中，xi+1描述的是粒子更新后的位置；xi代表的是粒子当前位置；μ描述的是惯性权重系数；c1、c2代表的是加速因子；vi+1、vi描述的是粒子更新后的速度和粒子初始速度；r1、r2为随机数，在区间[0，1]内取值。

5)将不发生变化的最终解和最大迭代次数设置为终止条件，满足终止条件时停止迭代，输出最优解，获得分子结构稳定性与影响因素之间存在的关系[7]。

2.2 稳定性评价指标

通过上述分析将吉布斯自由能和振动光谱作为分析碳族元素原子簇分子结构稳定性的指标。

1)吉布斯自由能

碳族元素原子簇结构的稳定性与吉布斯自由能之间呈反比[8]，碳族元素原子簇分子结构稳定性的仿真方法通过吉布斯自由能对碳族元素原子簇分子结构稳定性进行预估，通过下式计算碳族元素原子簇分子结构的吉布斯自由能Gunit

Gunit=Uv+Hunit-TS

(3)

式中，S代表的是碳族元素原子簇分子的熵值；Uv代表的是振动值；T代表的是温度；Hunit代表的是焓。

当碳族元素原子簇分子结构受到外部压力时，可通过下式计算Hunit

Hunit=Vunit+Uunit

(4)

式中，Vunit代表的是碳族元素原子簇分子的体积；Uunit代表的是内能。

碳族元素原子簇分子结构的内能Uunit可利用基于量子力学分块方法计算得到

(5)

式中，Eμ(n)描述的是第μ个分子在第n个碳族元素原子簇中对应的能量；Eμ(0)v(n)代表的是第μ个分子在第0个碳族元素原子簇中和第v个分子在第n个碳族元素原子簇中的二聚体能量。式(5)的第一部分描述的是所有单分子能量在第0个碳族元素原子簇中的求和；第二部分为比碳族元素原子簇中心给定阶段距离dcut短的QM相互作用能；第三部分描述的是第n个和第0个碳族元素原子簇之间存在的QM相互作用；利用ωB97XD/6-31G*在静电场中计算式(5)的前三项，可用电荷-电荷库伦互相作用描述距离大于dcut的两个碳族元素原子簇之间存在的相互作用[9]，式(5)的最后一项描述的是远距离静电之间存在的相互作用。

熵Sv的计算公式如下

(6)

式中，ωnk描述的是第n个存在波矢矢量k的分支对应的频率；β=1/k0T，其中k0描述的是玻尔兹曼常数。

零点振动能Uv的计算公式如下

(7)

2)振动光谱

通过下述公式计算动力常数矩阵D(rp，rq，k)

(8)

式中，H(rp，rq，k)描述的是第0个碳族元素原子簇中存在的p原子和第n个碳族元素原子簇中存在的q原子在平衡状态下对应的总能量二阶导数；mp、mq分别描述的是p原子、q原子对应的质量。

利用上式计算得到的动力学矩阵D(rp，rq，k)获得周期分子系统的正态模式和振动频率[10]。振动频率可以通过力常数矩阵d(0)计算得到，通过上述分析计算拉曼强度Rn0和红外强度In0

(9)

式中，Qn0描述的是正常模式；∂αii/∂Qn0、∂μi/∂Qn0分别描述的是碳族元素原子簇的极化率导数、偶极矩导数，可通过嵌入式分块量子力学方法计算得到。

3 分子结构稳定性分析

碳族元素原子簇分子结构稳定性的仿真方法在联系云概念的基础上实现碳族元素原子簇分子结构的稳定性分析。

设μp，ij代表稳定性评价指标j对应的指标值x0属于第i等级的确定度，可通过下式计算得到

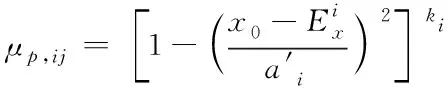
(10)

设up，i代表的是在等级i中样本P对应的综合确定度，其表达式如下

(11)

式中，λp，j描述的是稳定性评价指标对应的权重。

在最大隶属原子的基础上根据上式计算得到的综合确定度值判断碳族元素原子簇分子结构稳定性的等级L，实现碳族元素原子簇分子结构的稳定性分析

L=max{up，1，up，2，…，up，m}

(12)

4 实验与分析

为了验证碳族元素原子簇分子结构稳定性的仿真方法的整体有效性，需要对碳族元素原子簇分子结构稳定性的仿真方法进行测试，本次测试平台为Simulink。分别采用碳族元素原子簇分子结构稳定性的仿真方法(方法1)、基于粗糙集赋权的簇分子结构稳定性分析方法(方法2)和基于因子分析的分子结构稳定性分析方法(方法3)对碳族元素原子簇分子的结构稳定性系数进行测试，测试结果如图1所示。

图1 稳定性系数测试结果

分析图1中的数据可知，采用方法1在多次迭代中获得的稳定系数与实际稳定性系数基本相符，方法2和方法3获得稳定性系数与实际稳定性系数之间的偏差较大，通过上述分析可知，方法1可准确的对碳族元素原子簇分子结构的稳定性进行分析，因为方法1结合支持向量回归法和粒子群算法对分子结构稳定性与影响因素之间存在的关系进行分析，进而实现碳族元素原子簇分子结构的稳定性分析，提高了方法1的整体有效性。

方法1、方法2和方法3对碳族元素原子簇分子结构稳定性进行分析的相对误差如表1所示。

表1 相对误差测试结果

对表1中的数据进行分析可知，在多次迭代中采用方法1对碳族元素原子簇分子结构的稳定性进行分析时，相对误差均控制在2%以内，方法2和方法3对碳族元素原子簇分子结构的稳定性进行分析时，相对误差远远高于方法1的相对误差，因为方法1是根据碳族元素原子簇分子稳定性与影响因素之间的关系，在联系云概念的基础上分析其结构稳定性，降低了方法1的相对误差。

为了进一步验证碳族元素原子簇分子结构稳定性的仿真方法的整体有效性，对稳定性评价指标的可靠度进行测试，测试结果如图2所示。

图2 指标可靠度测试结果

对图2中的数据进行分析可知，碳族元素原子簇分子结构稳定性的仿真方法选取的稳定性评价指标可靠度在多次迭代中均高于80%，满足指标选取的标准，因为该方法利用支持向量回归法和粒子群算法分析了对碳族元素原子簇分子结构的稳定性产生影响的因素，选取吉布斯自由能和振动光谱作为稳定性评价指标，提高了指标的可信度。

5 结论

在材料和科学领域中碳族元素原子簇分子具有重要作用，为了将碳族元素原子簇应用在更广阔的领域中，需要对碳族元素原子簇分子结构的稳定性进行分析。目前分子结构稳定性分析方法的有效性较差，提出碳族元素原子簇分子结构稳定性的仿真方法，在联系云概念的基础上实现碳族元素原子簇分子结构的稳定性仿真，解决了目前方法中存在的问题，为碳族元素原子簇分子的应用奠定了基础。