不同力学模型的胶泥阻尼器比较与分析

刘昕运，马吉胜，吴大林

(陆军工程大学，河北 石家庄 050003)

1 引言

胶泥阻尼器出现以来，被广泛用于建筑、车辆、军工等行业。胶泥阻尼器内部含有独特的粘弹性材料，这种材料属于高分子硅氧有机聚合物，具有弹性和粘性双重特性。相比于常见的液压阻尼器和橡胶阻尼器，胶泥阻尼器结构更简单、容量更大、寿命更长、吸能率更高等特点[1]。

近年来，众学者对胶泥阻尼器的工作机理和力学性能的研究层出不穷。早期的力学模型大多基于实验和经验。Pekcan[3]对单出杆阻尼器进行不同频率拉伸压缩实验，提出了阻尼力与速度的幂函数呈正比。而后Terenzi[4]对单出杆粘弹型阻尼器和双出杆粘滞型阻尼器进行了实验，并在Pekcan公式的基础上进行了分析。Meram[5]为聚氨酯粘弹性阻尼器建立了Maxwell模型，Kelvin模型和Oscillation模型，并和实验结果进行比较。后来出现了将环形间隙的流动简化为平板间缝隙流动的思想。贾久红[6]和王虹琴[8]用微分的思想分析缝隙中的流体，推导出阻尼力正比于速度的幂函数，且阻尼系数与冲击实验环境、结构尺寸、粘度相关，但待定系数只能由实验确定。刘洪亮[9]、徐忠四[10]、仝志辉[11]等人对孔隙-缝隙式阻尼器进行分析，将流体运动分解为压差流、剪切流和孔隙流，推导出阻尼力的具体表达式，其中阻尼系数可由阻尼器结构尺寸直接求得。齐梦晓[12]在此基础上用AMESim液压系统仿真软件对胶泥阻尼器进行分析。随着流体动力学的发展，CFD技术开始应用于胶泥阻尼器的分析。郭强[13]和丁行武[14]建立双出杆孔隙式阻尼器的湍流CFD模型，并与正弦运动实验数据进行比较。孙靖雅[15]建立双出杆缝隙式阻尼器的层流CFD模型，并与落锤冲击实验数据比较。狄长春[16]建立了胶泥反后坐装置的三维流固耦合模型，并用射击实验进行验证。Wael Elsaady[17]建立磁流变阻尼器的湍流CFD模型，并进行了磁场和流场的数值计算。

以上研究是目前出现的针对各型胶泥阻尼器的常见方法。其中速度相关力学模型经过较大简化，参数确定较困难，准确性有限。而计算流体力学模型多数为正弦运动数值模拟，未进行速度冲击的数值模拟。且研究针对的阻尼器的结构和类型各不相同，无法横向对比。本文将以同型胶泥阻尼器为研究对象，基于计算流体力学和多体系统动力学，应用三种不同力学模型，经过静压实验的模型验证后，对阻尼器进行速度冲击仿真计算。分析和总结各方法的优缺点，为胶泥阻尼器的相关研究提供理论参考。

2 理论原理

2.1 阻尼器工作原理

目前出现的胶泥阻尼器有多种类型，按活塞杆结构可以分为单出杆式、等径双出杆式、非等径双出杆式。按活塞结构可以分为缝隙式、孔隙式、缝隙-孔隙式。本文选取较有代表性的非等径双出杆缝隙式胶泥阻尼器作为研究对象。如图1所示，该阻尼器主要由缸体、活塞、活塞杆、限位块和胶泥材料组成。相对等径双出杆式，其拥有自动弹性恢复的能力；相对单出杆式，同等力学性能下的活塞杆更粗，结构强度更大。胶泥在注入阻尼器时会被赋予一定的初始压力，这和限位结构能够保证阻尼器不受较小外力的扰动。当活塞和活塞杆向压缩方向运动时，缸体和活塞杆之间的空间变小，胶泥被压缩。弹性势能被储存，同时胶泥会流经环形间隙，产生阻尼力；当活塞和活塞杆向复原方向运动时，弹性势能被释放，胶泥向反方向流经环形间隙，继续耗散能量。

图1 胶泥阻尼器原理图

2.2 流体粘弹性模型

胶泥材料因其分子构型的独特性，在力学上既表现出液体的粘性，还有固体的弹性，且粘度比一般流体要大得多。工程上一般将胶泥材料的力学性能简化为kelvin模型，如式(1)所示，阻抗力为弹性力Fx和阻尼力Fv的叠加。

F=Fx+Fv

(1)

液体的可压缩性，本文均采用简化的Tait可压缩液体状态方程，如式(2)所示。液体的体积弹性模量用来衡量液体的可压缩性，体积弹性模量值越小液体越容易被压缩。在工程应用上体积弹性模量是液体的固有属性，由液体本身确定，其定义为在一定温度下，液体承受的压强改变单位大小时，液体体积的相对变化值的倒数，如式(3)所示

(2)

(3)

式中：m为液体密度指数；E为体积模量，且E=E0+nΔp；E0为参考体积模量；ρ为液体密度；ρ0为液体参考密度；p为液体压力；V为液体体积。

由于该阻尼器的最大压缩率不到1.5%，弹性模型的液体密度指数m可以视为1。由式(2)可以推导出弹性力Fk的表达式(4)

(4)

式中：ΔS为活塞两侧的面积差，也等于两端的活塞杆截面积差；p0为胶泥的初始压力；V0为胶泥的初始体积；x为阻尼器的压缩行程。

胶泥属于典型的非牛顿流体，不满足牛顿内摩擦定律，其粘度值会随着剪切力和剪切率的变化而变化。本粘度模型使用广义非牛顿流体的幂律本构方程，该模型认为粘度是剪切率的幂函数[18]，如式(5)所示

(5)

式中：K为稠度系数；n为流变指数，当n=1时，K=μ，流体为牛顿流体；当n>1时，表示流体具有剪切增稠特性，流体为非牛顿流体中的胀塑性流体；当n<1时，表示流体具有剪切稀变特性，流体为非牛顿流体中的拟塑性流体，大多数工业用高分子流体均为拟塑性流体，流变指数取值0.15～0.6之间。本阻尼器内所用胶质流体即为拟塑性流体。

2.3 平板流分析法

平板流分析法就是将通过环形间隙的流动简化为两平板间的纯剪切流动和纯压差流动的合成。本方法的特点是仅需通过阻尼器的结构参数就能确定阻尼力的函数解析式。平板间层流状态的压差流动的流量Q1如式(6)所示，剪切流动的流量Q2如式(7)所示[9]9-11]

(6)

(7)

式中：b为平板宽度，在阻尼器中等于π(D+D0)/2；l为平板长度，在阻尼器中等于活塞的厚度；h为两平板间缝隙宽度，在阻尼器中等于环形间隙宽度。

根据液体的连续性，得到通过环形间隙的总流量如式(8)所示。最终由式(6) (7) (8)推导得出阻尼器的阻尼力Fv如式(9)所示。式中：D为缸体内径；d1为较细活塞杆直径；d2为较粗活塞杆直径；D0为活塞直径。

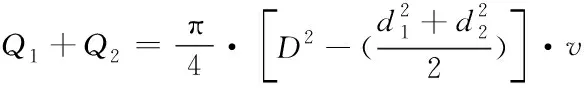
(8)

(9)

2.4 参数辨识法

多项研究表明，胶泥阻尼器的阻尼力近似满足式(10)所示的速度相关型表达式，其中阻尼系数C和流变指数n为恒定的未知参数。参数辨识法就是通过静压实验或者冲击实验辨识出未知参数，其特点是必须通过相关实验获取参数，具有模型较为准确，计算量小等优点。

Fv=Cvn

(10)

2.5 CFD数值分析法

胶泥阻尼器的CFD研究方法相对较新，这是利用现代强大的计算机能力对流体控制方程求数值解的研究方法。其特点是针对复杂流体问题的计算精度更高，后处理可以生成良好的可视化结果，但计算量更大，建模更加复杂。胶泥属于可压缩流体，在流体动力学中同样遵循质量守恒、能量守恒、动量守恒的基本物理规律。其对应着三个流体控制方程，连续性方程、能量方程、Navier-Stokes方程，如式(11)所示[19]。本方法需要用阻尼器的几何参数构筑流体网格模型，设置流体材料参数以及网格边界条件进行分析。

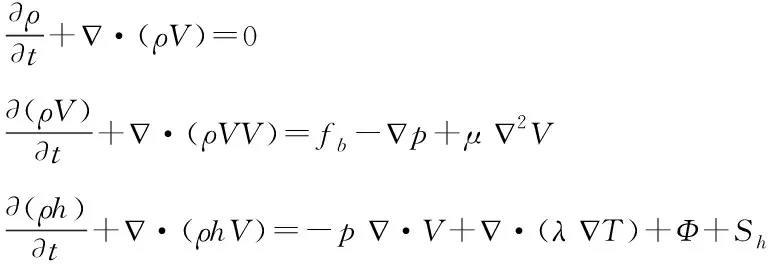
(11)

式中：ρ为流体密度；V为流体速度矢量；fb为体积力；p为压差力；μ为动力粘度；h为流体比焓；λ为导热系数；Φ为粘性耗散项；Sh为流体源项。

3 模型建立

在建立MBD模型和CFD模型之前，首先对胶泥阻尼器的CAD模型进行几何清理，简化结构便于后期建模，胶泥阻尼器的几何结构如图2所示。

图2 阻尼器几何模型

3.1 MBD模型

平板流分析法和参数辨识法均在多体系统动力学软件Recurdyn中进行计算。如图3所示，用固定副连接缸体和地面，用平移副连接活塞杆和缸体。在两者之间设置两个函数力，其中弹性力根据式(4)设置，阻尼力分别根据式(9)和式(10)设置，阻尼力的方向变化用IF(VX)函数控制。

图3 阻尼器MBD模型

3.2 CFD模型

CFD数值分析在流体动力学软件ANSYS/Fluent中进行计算。抽取活塞杆和缸体之间流体域的几何，划分三维六面体结构网格。为实现活塞边界的移动，以活塞的圆柱面为分界面，采用Mesh Interface的方法划分合并网格。如图4所示，六面体结构网格总数约为140万个。材料密度设置为可压缩液体模型，粘度设置为幂律非牛顿模型。使用k-ε湍流模型和标准壁面模型，并为流体设置大小为p0的初始压力，以保证缓冲器的初力。由于活塞的轴向运动，涉及到网格边界移动和网格重构，为保证重构网格的质量，采用Layering动网格层铺法。

图4 阻尼器CFD网格

4 静压实验与模型验证

本文用胶泥缓冲器的静压实验数据验证和比较以上三种模型。静压实验在CSS-55100型万能试验机上进行，固定住缸体，匀速的压缩和复原活塞杆，用计算机记录获得的压力数据和位移数据，通过数据处理获得静压阻抗力-位移滞回曲线。

平板流分析法能够不通过静压实验直接得到阻尼力和速度的关系式，其MBD模型静压过程的计算结果如图5(a)所示。与实验数据相比，其压缩过程的阻抗力更大，复原过程的阻抗力更小，说明平板流分析模型在静压过程中的阻尼力比实际阻尼力大，模型的准确性有限。参数辨识法需要使该模型计算输出的数据接近实验数据，以此获取未知参数，故参数辨识模型静压过程的计算结果非常接近实验曲线，如图5(b)所示。CFD数值分析法，通过材料和边界设置等直接获得静压仿真结果，同样不需要提前实验，静压过程的计算结果如图5(c)所示。可以看到CFD数值模型的静压分析结果也非常接近实验曲线，验证了所建立的CFD模型的准确性，这是下一步冲击过程模拟的基础。

图5 静压滞回曲线

5 冲击过程模拟

为比较三种模型在冲击过程中的计算结果，设置相同的冲击质量13.5kg和冲击速度8m/s。在已建立的MBD模型的基础上，设置负载质量和初始速度，进行平板流分析模型和参数辨识模型的冲击仿真计算。而CFD冲击模型和静压模型的边界条件不同，在计算之前无法明确知道每个时刻的阻尼器运动状态。这属于被动运动问题，也属于流固双向耦合问题[20]。在建立的静压CFD模型的基础上，使用6DOF动网格模型来模拟这种问题，限制活塞边界的3个旋转自由度和2个平移自由度，设置负载质量和初始速度，并限制边界的位移量在几何结构允许的范围内。

图6为入膛冲击过程中的流体速度和流线分布结果，由于模型是三维的，纵切面上的一些流线不能被连续显示。CFD分析结果显示阻尼器整个压缩复原过程用时7.7ms，2.2ms时刻达到最大压缩行程。速度最大区域分布在环形间隙中，其次在活塞两侧。压缩过程中，随着缓冲器的压缩，流体最大速度从25m/s逐渐减小至1m/s以下。复原过程中，流体最大速度在5-6mm/s范围保持稳定，直到复原到位。胶泥拥有较大的动力粘度，这让流线保持平稳，不会出现较大的涡旋。值得注意的是，从8ms时刻的速度云图看到，虽然7.7ms时活塞已经复进到位，但是胶泥并未停止流动，仍然有0.26m/s的流速，直到10ms流体的流动才几乎停止。这些可视化的流动现象更加贴近实际，是平板流分析模型和参数辨识模型无法模拟的。

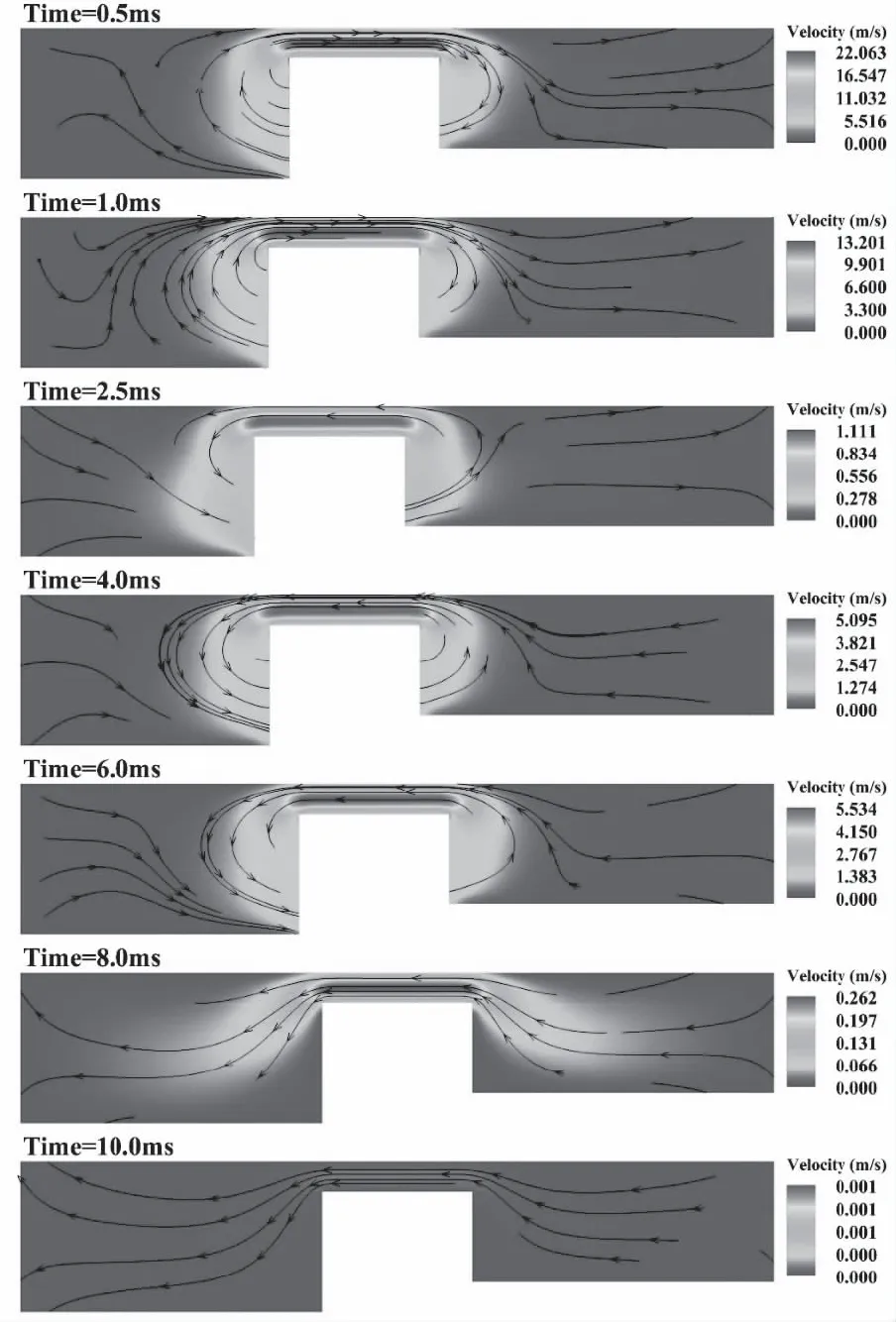
图6 冲击分析的速度云图

对三种模型运行冲击过程仿真计算后，输出阻抗力-位移滞回曲线进行比较，如图7所示。平板流分析模型压缩过程中阻抗力持续减小，最大阻抗力为58289N。复原过程中阻抗力先减小至0，再反向增加然后减小，最大反向阻抗力为650N。其最大压缩行程为7.38mm。参数辨识模型在压缩过程中的阻抗力先小幅增大再减小，最大阻抗力为41937N。复原过程中阻抗力先逐渐减小至0，再反向增加，最大反向阻抗力为3058N。CFD数值分析模型在压缩过程中阻抗力先增大后减小，最大阻抗力在三种模型中最大，达到92200N。复原过程中阻抗力先逐渐减小至0，再反向增加，最大反向阻抗力为3033N。其最大压缩行程为6.93mm。

图8为单独分离的阻尼力和速度的关系，其中横坐标正方向代表压缩方向，负方向代表拉伸方向。由于平板流分析法和参数辨识法的阻尼力的本构关系式的构型是一样的，不一样的是一些参数，故这两种分析方法的阻尼力曲线非常相似，且阻尼力与速度是单调的关系，随着速度减小阻尼力是持续减小的。而CFD分析法的阻尼力并不是单调的，压缩刚开始时，随着压缩速度减小，阻尼力先增大后减小。这是由于实际情况下，冲击刚开始时胶泥流体还来不及通过环形间隙产生阻尼力，此时的弹性力占主导地位。但随着压缩行程的增加，阻尼力逐渐变为平稳下降的趋势。而在拉伸复原过程中不会出现这种情况，阻尼力和速度呈正相关。这说明了阻尼力在阻尼器的启动过程中存在特异性。以上曲线均显示CFD数值模型的力学性能更加贴近实际，其准确性最高。

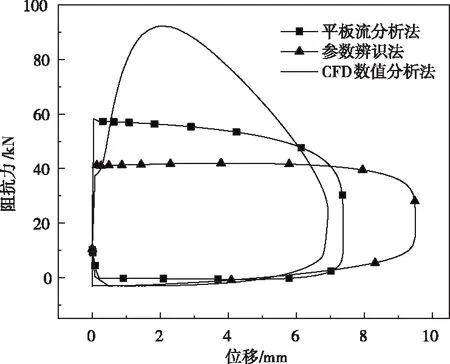
图7 冲击滞回曲线

图8 阻尼力-速度曲线

6 结论

本文系统地建立了关于胶泥阻尼器的三种常见力学模型，并进行计算和比较。其中平板流分析法和参数辨识法通过MBD建模和计算，计算流体动力学分析法通过CFD建模和计算。通过分析和总结，得到一些结论：

1) 三种建模方法经过实验验证，均能够在一定程度上反映阻尼器的力学性能。其中CFD数值模型经过实验验证结果最为准确，能够可视化的模拟出流体的细节，但建模过程复杂，几何参数改变困难；平板流模型经过大量简化，无需实验辅助就能得到阻尼力参数化表达式，几何参数改变容易，计算速度较快，但准确度有限，和实验结果贴合度较低；参数辨识模型同样经过大量简化，由于需要实验辅助参数辨识，和实验结果贴合度较高，但几何参数同样不易改变。

2) CFD数值分析模型能够模拟出胶泥阻尼器在冲击刚开始时的阻尼力特异性，以及活塞杆恢复到位时的流体未静止的现象，而其它两种模型不能。

3) 通过分析和比较，建议在对胶泥阻尼器进行几何设计和参数优化时使用平板流参数化模型，在定型分析和力学研究时使用更为精确的CFD数值模型。

4) 本研究仅针对特定的“缝隙式”胶泥阻尼器研究对象进行分析，有一定局限性。进一步的研究可以针对“孔隙式”和“孔隙-缝隙式”阻尼器进行全面的分析和比较。