中低速磁浮车辆-道岔主动梁刚柔耦合振动分析

唐语，刘放，邹逸鹏，庞振华

（西南交通大学 机械工程学院，成都 610031）

磁悬浮列车是一种无接触的地面轨道交通系统，它以速度快、爬坡能力强、转弯半径小、经济环保等优势被认为是21 世纪交通工具发展的方向[1]。目前，国内外学者对道岔进行了一系列研究。任晓博[2]通过分析长沙磁浮车辆和双线简支桥梁，列出了车辆-桥梁耦合振动方程并采用ANSYS APDL 语言编程进行了动力学响应及控制仿真分析。王党雄等[3]对磁浮列车-桥梁系统进行了耦合振动特性分析，运用实验和仿真的对比证明了可以将磁浮列车简化为均布荷载进行分析。Zheng 等[4]建立了5 自由度磁浮列车模型，分析了考虑耦合振动与不考虑耦合振动的车体及桥梁动力响应的差异。以上论文主要研究了磁浮列车及轨道的设计，多刚体动力学分析以及实验中的表现，而很少对磁浮道岔梁进行柔性体耦合振动分析。磁浮轨道梁的截面是相同的，而磁浮道岔梁的截面是不断变化的。磁浮道岔是磁浮列车行驶过程中的薄弱环节，道岔梁的主要材料是Q235，因为这种钢结构没有阻尼，在轨道不平顺激励和磁浮车体悬浮架的振动影响下，车辆-道岔容易发生耦合振动，造成打轨或更严重事故[5]。而且仅仅将道岔梁简化为刚体和弹簧阻尼的结合对模拟实际情况可能有误差情况，因此对磁浮道岔进行刚柔耦合振动分析具有重要意义。

磁浮道岔的稳定性对磁浮车辆行驶过程中的人员安全至关重要，道岔的刚度和强度必须满足要求，道岔自身的结构特性也应能承受车辆行驶引起的振动变形。本文以某36 t 满载磁浮车体和某单跨16.5 m 中低速磁浮道岔主动梁为研究对象，分析车辆-道岔梁的耦合振动情况，主动梁跨中截面图如图1 所示。

1 车辆-道岔梁动力学方程的建立

1.1 主动梁等效刚度的求解

磁浮列车在道岔主动梁上行驶时，悬浮架上的悬浮电磁铁对主动梁产生均匀压力。磁浮列车行驶至主动梁两端附近时，由于其下有支座支撑，则主动梁变形较小；当磁浮列车行驶至主动梁正中时，由于此时离支座最远，所以其竖向变形最大。为了得到主动梁纵向等效刚度，采用ANSYS 有限元软件对主动梁进行静力学仿真计算，得到施加均匀载荷和约束条件下主动梁应变图。然后在主动梁上选取若干个应变测量点，得到主动梁竖直方向上的应变与纵向距离的函数关系为x(l)。设主动梁上施加的均匀载荷大小为P，则由P=kx得到刚度与主动梁纵向距离的函数关系为k(l)，即为等效刚度。主动梁板厚为30 mm，35 mm，40 mm 的等效刚度曲线如图2所示。

图2 主动梁等效刚度曲线

1.2 随机激励

受轨道随机不平顺激励的影响，车辆-轨道耦合系统会产生随机振动，车辆的振动又会加剧轨道不平顺状态的恶化，在实际线路上各种轨道不平顺与线路里程有关的复杂随机过程[6]。从功率谱中可以看出各波的特性以及轨道不平顺的频域变化。常见的轨道不平顺功率谱有美国轨道谱，德国轨道谱及中国轨道谱，本文采用德国轨道谱[7]，其高低不平顺公式为

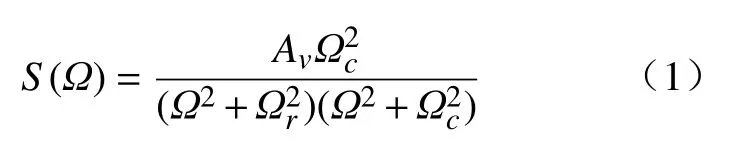
式中：S(Ω)轨道功率谱密度，cm2/（rad/m）；Ω轨道不平顺的空间频率，rad/m；Ωc及 Ωr为截断频率，rad/m；Av粗糙度系数，m2/（rad/m）；

因为中低速磁浮列车过道岔时速度不大于250 km/h，则采用高干扰轨道级别德国轨道谱粗糙度系数及截断频率，由文献[8]可取Av=1.08×10-6，Ωc=0.824 6，Ωr=0.020 6。

采用时域模拟法[9]和傅里叶变换对上述不平顺谱进行频域-时域转换，得到轨道不平顺模型，如图3所示。

图3 主动梁轨道不平顺样本

2 车辆-道岔梁刚体动力学分析

2.1 动力学方程的建立

采用刚体动力学分析主动梁时，需要将整个系统抽象为力学系统，主动梁受到磁浮车体和悬浮架重力及轨道不平顺激励，并在其作用下产生振动。为了分析整个系统的受力情况，将主动梁视为刚体和无数弹簧阻尼的集合，于是将整个系统视为3 阶弹性阻尼系统，采用拉格朗日方程[10-11]对其建立数学模型，即

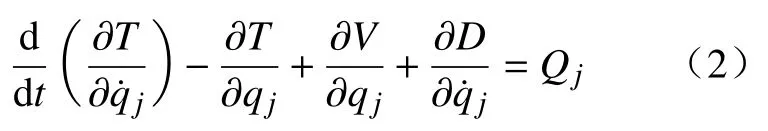
式中：T是动能；V是势能；qj表示广义坐标；Qj表示相对应的广义力；D表示能量耗散函数。

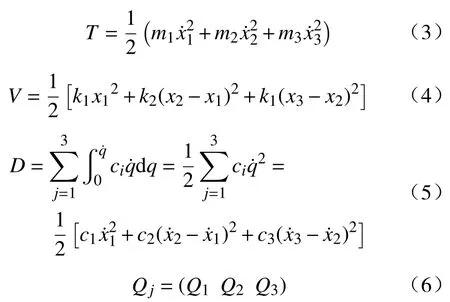
计算后得到：

式中：k1表示主动梁刚度；k2表示悬浮架刚度；k3表示空气弹簧刚度；c1表示主动梁阻尼；c2表示悬浮架阻尼；c3表示空气弹簧阻尼；m1表示主动梁质量；m2表示悬浮架质量；m3表示磁浮车体质量；x1表示主动梁位移；x2表示悬浮架位移；x3表示车体位移；G表示轨道不平顺激励。

2.2 刚体动力学仿真

采用SIMPACK 软件对主动梁采取刚体动力学仿真。在SIMPACK 中，将主动梁与地面铰接，两端设置43 号力元（六轴弹性运动连接）模拟主动梁刚度；悬浮架与主动梁采用50 号力元（施加力函数表达式）模拟悬浮电磁铁磁力；车体与悬浮架采用43 号力元模拟空气弹簧。其二维拓扑图如图4 所示。

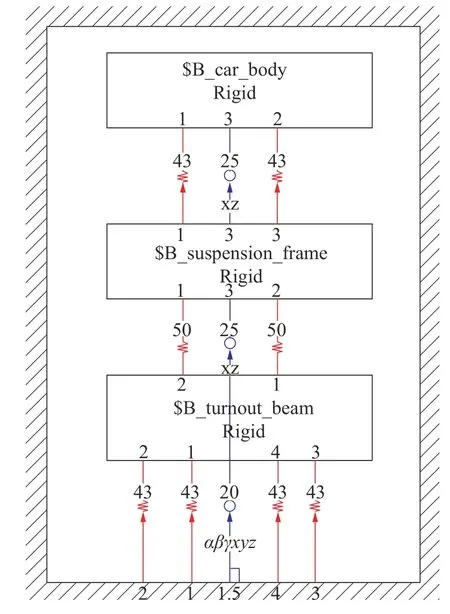
图4 多刚体仿真拓扑图

设置悬浮架以60 km/h 速度匀速行驶，主动梁板厚为30 mm，35 mm，40 mm 时的主动梁垂向位移时域曲线如图5 所示。

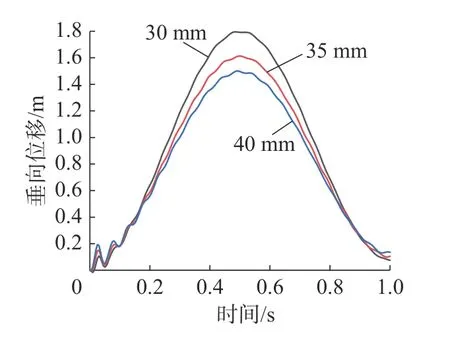
图5 多刚体仿真结果图

由仿真结果可知，主动梁板厚为30 mm 时，主动梁中点最大位移为1.80 mm；主动梁板厚为35 mm时，主动梁中点最大位移为1.62 mm；主动梁板厚为40 mm 时，主动梁中点最大位移为1.51 mm。所以增加梁刚度，增加梁重量是减少梁振动的有效方法。

3 车辆-道岔梁刚柔耦合振动分析

主动梁是磁浮道岔梁中跨度最大，长度最长的梁，为了更好的得出与实际相近的仿真结果，对中低速磁浮道岔主动梁进行刚柔耦合振动分析。因为车体和悬浮架的变形对道岔梁的变形影响较小，所以在分析道岔的变形时，将道岔梁作为柔性体，车体和悬浮架视为刚体，对其进行刚柔耦合振动分析。

该分析建立的模型自由度很大，目前还没有软件能较好解决此类问题，一般通过编制仿真程序或采用多个软件进行联合仿真。本文采用ABAQUS和SIMPACK 进行联合仿真，对中低速磁浮车辆-道岔主动梁进行刚柔耦合振动分析。

为了得到道岔梁的柔性体模型，首先将主动梁三维模型保存成xt 格式，导入ABAQUS 中，然后设置材料参数（密度7 850 kg/m3，弹性模量210 GPa，泊松比0.3），并划分网格，设置约束，约束类型为耦合，耦合类型设置为连续分布。为了进行单元缩聚，降低其模型自由度，提高计算效率[12]，设置了模态分析[13]和子结构分析[14]两个分析步。并在子结构分析中计算减缩质量矩阵，减缩结构阻尼矩阵及减缩粘性阻尼矩阵，得到inp 和sim 文件。

完成ABAQUS 软件操作后，将导出的文件导入SIMPACK，利用File Generation 刚柔耦合接口将inp 和sim 文件转化为fbi 文件，然后将柔性道岔梁设置在SIMPACK 中。联合仿真流程图如图6所示。

图6 联合仿真流程图

在SIMPACK 中，将主动梁与地面铰接，两端设置43 号力元模拟主动梁支撑；悬浮架与主动梁采用50 号力元模拟悬浮电磁铁磁力；车体与悬浮架采用43 号力元模拟空气弹簧，其二维拓扑图如图7 所示。

图7 柔性体仿真拓扑图

为减少计算量，车体和悬浮架设计为刚体，在动力学分析中物体具有质量，质心，转动惯量等参数，不会发生形变。所以可以采用简化模型导入得出，其动力学模型如图8 所示。

图8 车岔耦合动力学模型

设置悬浮架以60 km/h 速度匀速行驶，得到主动梁板厚为30 mm，35 mm，40 mm 时主动梁垂向位移时域图像，如图9 所示。

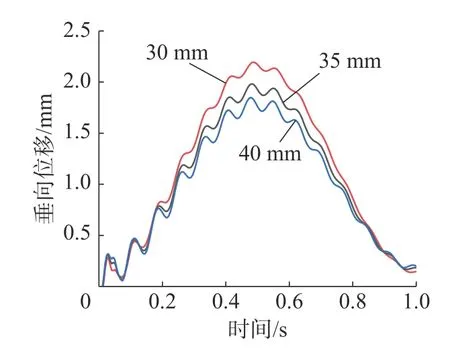
图9 柔性体仿真结果图

由仿真结果可知，主动梁板厚为30 mm 时，主动梁跨中垂向位移为2.17 mm；主动梁板厚为35 mm时，主动梁跨中垂向位移为1.96 mm；主动梁板厚为40 mm 时，主动梁跨中垂向位移为1.82 mm。与刚体分析中主动梁板厚对比，柔性体主动梁垂向位移要比刚体主动梁位移大很多。使用柔性体主动梁进行刚柔耦合振动分析更与实际情况接近。

4 结论

1）基于中低速磁浮道岔主动梁的承载结构特征，通过计算主动梁纵向多点应变建立道岔梁纵向等效刚度曲线，然后采用拉格朗日动力学方程的方法建立车岔耦合振动动力学模型，并采用SIMPACK进行刚体仿真。然后用ABAQUS 将主动梁有限元模型进行模态分析和子结构分析，得到结果与SIMPACK 进行联合仿真。

2）对中低速磁浮道岔主动梁进行刚体动力学分析，得到列车以60 km/h 速度通过主动梁时梁板厚为30，35，40 mm 时的垂向位移分别为2.09，1.84，1.68 mm。小于危险值[15]，但主动梁板厚对主动梁变形影响很大，增加梁刚度和增加梁重量是减少梁振动的有效方法。

3）将主动梁模型转换为柔性体，悬浮架和车体为刚体进行刚柔耦合分析时，得到列车以60 km/h速度通过主动梁时梁板厚为30，35，40 mm 时的最大应变分别为2.19，1.97，1.82 mm，小于危险值。得出仿真过程中，将主动梁转化为柔性体进行刚柔耦合分析得出的垂向位移量大于刚体动力学分析的垂向位移量。柔性体主动梁更能真实地反映车辆系统的动力学性能。