钢筋混凝土桥墩拟静力正交试验及数值模拟

李贵乾　唐光武　郑罡

摘 要：為系统研究多参数组合对圆形钢筋混凝土桥墩延性抗震性能的影响，建立较可靠的数值分析模型，开展了以墩高（剪跨比）、纵筋率、轴压比、配箍率为因素的四因素三水平圆形钢筋混凝土桥墩拟静力弯曲破坏正交试验，并基于OpenSees纤维模型及等效塑性铰模型对试验桥墩的骨架曲线、滞回性能进行数值分析。结果表明：试验桥墩位移延性为5.3～8.4，等效粘滞阻尼比为0.19～0.29，具有良好的抗震性能;在置信度为0.1的水平下，墩高、纵筋率对极限位移有显著影响，剪跨比、纵筋率对最大侧荷载有显著影响，纵筋率对累计耗能有显著影响，剪跨比、轴压比对等效屈服弯曲刚度有显著影响，且除剪跨比与最大侧向荷载呈负相关关系外，其余均呈正相关关系;数值分析结果与试验结果吻合良好，基于等效塑性铰模型的截面层次及构件层次的数值模拟均可作为钢筋混凝土桥墩抗震性能评估的有效方法。

关键词：桥墩;抗震性能;拟静力试验;正交试验;等效塑性铰模型;数值模拟

中图分类号：U443.22 文献标志码：A 文章编号：2096-6717（2022）04-0113-11

Quasi-static orthogonal tests and numerical simulations of reinforced concrete bridge piers

LI Guiqian1， TANG Guangwu2， ZHENG Gang3

（1. Guangxi Vocational and Technical College of Communications， Nanning 530216， P. R. China;2. State Key Laboratory of Bridge Structural Dynamics， China Merchants Chongqing Communications Technology Research & Design Institute Co.， Ltd.， Chongqing 400067， P. R. China; 3. School of Civil Engineering， Chongqing Jiaotong University， Chongqing 400074， P. R. China）

Abstract： In order to systematically study the influence of multi-parameter combinations on the seismic performance and establish a reliable numerical analysis model of circular reinforced concrete piers， a quasi-static orthogonal test of four-factors and three-level for circular reinforced concrete bridge piers has been carried with pier height （ shear span ratio ）， longitudinal reinforcement ratio， axial compression ratio and stirrup ratio as factors.Then the skeleton curve and hysteretic behavior of specimens were simulated with fiber model and equivalent plastic hinge model using OpenSees platform. The results show that all test piers have good seismic performance，the displacement ductility is between 5.3 and 8.4， and the equivalent viscous damping ratio is between 0.19 and 0.29. At the level of confidence of 0.1， the pier height and longitudinal reinforcement ratio have a greater influence on the ultimate displacement， the aspect ratio and longitudinal reinforcement ratio have a significant effect on the maximum lateral load， the longitudinal reinforcement ratio has a significant impact on the cumulative energy， the aspect ratio and axial load ratio have a greater impact on the equivalent stiffness， and the aspect ratio is negatively correlated with the maximum lateral load， the rest are all positively correlated. The force-displacement relationship curves of bridge piers derived from the fiber element model agree well with experimental results.Both numerical simulation of the section-level and component-level based on equivalent plastic hinge model can be used as an effective method to evaluate the seismic performance of reinforced concrete bridge piers.

Keywords：bridge piers; seismic performance; quasi-static test;orthogonal test;equivalent plastic hinge model; numerical simulation

随着桥梁抗震技术的进步，美国Caltrans规范[1]、美国AASHTO规范[2]、欧洲Eurocode 8规范[3]以及日本JRA规范[4]等主要桥梁抗震规范均已采用延性设计。中国在2008年5·12汶川地震后颁布的《公路桥梁抗震设计规范》[5]（JTG/T 2231-01—2020，以下简称《规范》）中引入了延性抗震的设计理念，以替代基于准强度设计、缺少延性抗震细节的《公路工程抗震设计规范》（JT 004—89）[6]。圆形、矩形桥墩在桥梁工程中均被广泛使用，在需要考虑地震作用的桥梁设计过程中，圆形钢筋混凝土桥墩因其延性抗震性能各向同性，在桥墩选型时受到桥梁工程师青睐。

为研究圆形钢筋混凝土桥墩的延性抗震性能，学者们进行了广泛的试验研究及数值分析。在试验研究方面，Lehman等[7]为量化钢筋混凝土桥墩的抗震性能指标，对10个圆形桥墩进行了拟静力试验，研究了5个因素（剪跨比、纵筋率、配箍率、轴压比及加密区长度）的影响，结果表明，纵筋屈曲对桥墩的破坏影响较大，轴压比、配筋率对保护层混凝土的剥落无明显影响;王君杰等[8]则用11个圆形桥墩进行试验，研究了4个因素（混凝土强度、纵筋强度、箍筋强度及箍筋间距）的影响，结果表明，纵筋强度、箍筋间距的影响较明显，箍筋强度、混凝土强度的影响较小。Trejo等[9]、Barbosa等[10]亦通过拟静力试验考察了3个因素（剪跨比、纵筋率与纵筋强度）对圆形桥墩抗震性能的影响，结果显示，纵筋率对耗能影響较大;Barcley等[11]的试验结果则表明，将普通钢筋换为高强钢筋对圆形墩的纵筋屈曲和耗能影响不大，但会使纵筋在较低的位移水平下断裂。从以上研究可以看出，在考虑圆形钢筋混凝土桥墩的抗震性能时，至少有8个因素（混凝土强度、纵筋强度、箍筋强度、剪跨比、轴压比、纵筋率、配箍率、箍筋间距）受到学者们的关注，并已得出若干重要的定性或定量结论，但各因素对桥墩延性抗震性能的影响趋势及程度尚无完全一致的认识。在这些试验工作的基础上，选择工程界关心的多个重要因素进行系统性试验，并对多参数组合下的极限位移、极限荷载、极限耗能和有效刚度等抗震性能特征值进行较严格的数学检验，有助于对桥墩延性抗震性能更准确、深入的理解和把握。

在数值分析方面，Su等[12]采用纤维梁柱单元对5个混凝土强度、纵筋屈服强度不同的圆形桥墩拟静力试验结果进行了数值分析;成虎等[13]则基于OpenSees纤维单元对PEER的圆形足尺桥墩振动台试验结果进行了数值模拟。以上模拟均采用分布塑性的非线性梁柱单元，同时考虑墩底主筋滑移效应，取得了较好的模拟效果。但分布塑性模型与桥梁抗震规范所采用的集中塑性模型（即等效塑性铰长度）的基本概念差异较大，不便于根据规范内容指导桥墩的抗震设计及性能评估。

笔者将正交试验设计方法引入桥墩拟静力试验研究中，进行以墩高（剪跨比）、纵筋率、轴压比、配箍率为因素的四因素三水平桥墩拟静力正交试验，分析桥墩的力位移曲线特性、延性指标、等效阻尼比及累计耗能等重要参数，并通过方差分析研究各因素对极限位移、最大侧向荷载、累计耗能及有效弯曲刚度的影响程度。同时，为契合规范集中塑性模型的基本概念，并从简便应用和精细模拟两个层次考虑，基于OpenSees的零长度截面单元、集中塑性铰单元，配合等效塑性铰模型，对试验桥墩进行截面层次和构件层次的数值模拟，并与试验结果进行对比分析。

1 试验设计

正交试验主要考察墩高（剪跨比）、纵筋率、轴压比、配箍率等4个因素对弯曲破坏形态桥墩抗震性能的影响，每一因素设置3个水平，根据正交试验设计方法，共需进行9个桥墩试验。

1.1 模型设计

试件采用圆形钢筋混凝土桥墩，几何尺寸主要参考PEER墩柱性能数据库中圆形墩相关参数及试验设备条件确定，纵筋率、箍筋率和构造细节等满足《规范》相关规定，轴压比范围符合桥墩受力特征，以研究满足《规范》各项要求的圆形钢筋混凝土桥墩的抗震性能及各因素影响情况。桥墩试件主要参数见表1，几何尺寸及钢筋布置见图1，各试件截面直径D均为40 cm，主筋根数均为12根，箍筋采用螺旋箍筋。

1.2 材料特性

桥墩试件采用C30混凝土制作，基座及墩身混凝土28 d强度f′c实测值分别为33.9、31.9 MPa。主筋采用HRB335螺纹钢筋，直径分别为10、14、18 mm，对应的屈服强度fy分别为394、332、374 MPa;螺旋箍筋采用R235光圆钢筋，直径为8 mm，屈服强度为278 MPa。

1.3 试验加载装置及加载历程

试验加载装置如图2所示，侧向加载全程采用位移控制。加载历程分为3个阶段：开裂前、屈服前、屈服后，位移加载历程见图2。开裂前、屈服前的位移水平分别以墩底截面混凝土开裂及纵筋首次屈服为标志，并按弹性理论计算;屈服后的位移水平按理论屈服位移Δcy的倍数确定，每一位移水平往复循环加载3次。理论屈服位移Δcy以截面弯矩曲率分析所得的等效屈服曲率，并考虑剪切变形和纵筋滑移变形来计算，各桥墩的理论屈服位移Δcy依次为12、14、17、20、22、25、32、29、36 mm。试验的终止条件为桥墩的侧向承载力下降到最大值的85%以下、纵筋断裂或者丧失竖向承载力。

应该说明的是，在制作过程中，C7024墩墩底塑性铰区混凝土振捣欠密实，拆模后孔洞较多，后期仅用水泥浆敷面处理，存在一定的施工缺陷。

2 试验现象及结果

2.1 破坏过程及特征

所有桥墩均为明显的弯曲破坏，试体的损伤破坏过程基本相同，最终破坏时，墩底形成所谓的“塑性铰”。破坏过程可概括为：1）混凝土开裂，弯曲裂缝增多;2）钢筋屈服，弯曲裂缝贯通;3）墩身轴线附近形成斜裂缝，保护层混凝土开始剥落;4）箍筋和纵筋裸露，混凝土剥落区域逐渐稳定;5）箍筋明显变形、错位，纵筋失去箍筋约束开始屈曲;6）约束混凝土有压溃征兆，纵筋严重屈曲后断裂。图3为C4515墩破坏过程及最终破坏形态的试验照片。试体桥墩最终破坏时，纵筋直径为10 mm的试体约束混凝土压溃、剥落现象不明显，主要以纵筋断裂控制破坏;纵筋直径为14、18 mm的试体约束混凝土压溃、剥落现象较明显，以约束混凝土压溃、纵筋断裂双重控制破坏。

在5倍理论屈服位移180 mm级循环加载过程中，C7024墩因墩底混凝土存在一定的施工缺陷，其保护层混凝土大面积压溃、剥落，约束混凝土亦有压溃迹象，随后纵筋开始屈曲、断裂，抗震性能未能达到预期目标。

2.2 桥墩力位移滞回曲线

图4给出了9个试体桥墩的墩顶力位移滞回关系曲线，并在滞回曲线上标识了相应的损伤状态。滞回环均呈梭形，特点如下：屈服前，滞回环面积较小，同一位移3次循环加载间刚度无明显变化，处于基本弹性状态;屈服后，滞回环越来越饱满，面积逐渐增大，同一位移作用下，后一循环的滞回环明显比前一循环更窄、更细;经历最大荷载后，随着加载位移的增加，滞回环愈加饱满，逐渐出现捏拢现象;接近位移极限状态时，纵筋开始屈曲、疲劳断裂，同一位移作用下，后一循环的强度、刚度相比前一循环显著减小，滞回环迅速捏拢。

3 试验结果分析

3.1 骨架曲线

为便于桥墩强度、变形等抗震性态的定性比较，需作出各桥墩滞回曲线的骨架曲线，定义为各位移水平下首次循环加载位移峰值点的连线。图5给出了各桥墩的骨架曲线，由图可知：桥墩侧向承载力随剪跨比的增大而降低，随纵筋率的增大而提高，且轴压比作用较大时，提高更明显;桥墩侧向位移能力随墩高及纵筋率的增大而增大;循环加载位移逐渐增大时，随着混凝土的剥落、纵筋的屈曲及断裂，骨架曲线出现不同程度的下降段。

3.2 延性能力

延性能力可体现结构的耗能和变形能力，是评估桥墩抗震性能的重要指标。延性能力采用极限位移Δu和屈服位移Δy之比，即位移延性系數μΔ来表示。

μΔ=Δ/Δ（1）

屈服位移Δy根据Park[14]的方法确定，如图6所示，图中圆圈位置即为等效屈服点，极限位移Δu定义为侧向承载力降低到最大值的85%时所对应的位移。如侧向承载力未降低到最大值的85%以下，则极限位移Δu取为纵筋首次断裂所对应的循环

位移峰值，屈服位移Δy与极限位移Δu取正、负加载方向的均值。由表2可知：试验桥墩的位移延性系数在5.3～8.4之间时，表现出良好的延性性能，具备较好的塑性变形能力和抗倒塌能力;C7024墩由于墩底区域存在一定的施工缺陷，在试验过程中过早破坏，位移延性系数小于其他桥墩，但仍大于5，延性能力仍处于较高水平。

3.3 强度退化

为反映桥墩在整个加载历程中的强度退化特性，引入强度退化系数αi。

α=V/V（2）

式中：Vi为各级目标位移第一次循环达到时的侧向最大荷载;Vmax为正、负加载方向各自骨架曲线中最大荷载的绝对值，如图6所示。图7给出了αi随位移延性系数的变化曲线，且与极限状态荷载0.85Vmax对应的αi=0.85和αi=-0.85水平线进行比较。由图7可见，各桥墩在经历等效屈服点后（位移延性系数为1.0）均有较长的水平段，表明桥墩强度不会立即退化，即使达到最大荷载后，仍能继续承受荷载;当经历极限状态荷载点后，承载能力迅速下降。

3.4 耗能特性

桥墩耗能特性反映了桥墩耗散地震能量的能力，桥墩的累计耗能定义为图4中力位移滞回曲线各封闭滞回环所包围的面积之和。每一加载位移对应3个滞回环，一个滞回环所耗散的能量Wi如图6所示，将位移极限状态前的所有滞回环面积相加，即为桥墩位移极限状态下的累计耗能。

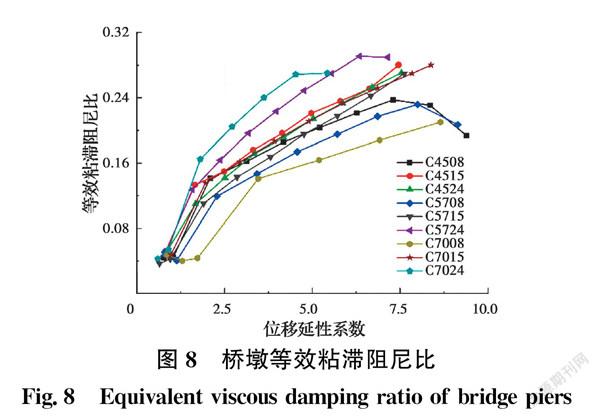
等效粘滞阻尼比ξeq定义为一个循环的耗能与等价线弹性体的应变能之比，亦可作为桥墩耗能能力的表征，其计算公式为

式中：Ki和Δi分别为各级目标位移第一次循环达到时的割线刚度和最大位移值（如图6所示），取正、负加载方向的均值。

表2给出了各桥墩位移极限状态下的累计耗能值，图8给出了各桥墩等效粘滞阻尼比随位移延性系数的变化曲线，可见各桥墩等效粘滞阻尼比的变化趋势基本一致。位移极限状态达到前一循环的等效粘滞阻尼比ξeq在0.19～0.29之间（见表2），表明试体桥墩具有较强的耗能能力，耗能指标满足抗震设计要求。

4 数值模拟

4.1 截面层次

采用OpenSees零长度截面单元ZeroLengthSection Element[15]及等效性铰模型对墩顶力位移骨架曲线进行截面层次的模拟，零长度截面单元用于桥墩截面P-M-分析。为模拟墩顶力位移骨架曲线，假定如下等效塑性铰模型：墩底截面曲率b小于或等于等效屈服曲率y时，墩顶位移ΔT按 bL2/3计算;b大于y时，墩底出现塑性铰，其等效长度Lp保持定值，墩顶位移ΔT按式（5）确定;将侧向力取为各曲率b对应弯矩Mb与墩高L的比值（弯矩Mb考虑墩顶轴力的P-Δ效应），即可得到相应的骨架曲线。

因截面P-M-分析仅能考虑弯曲效应，而墩顶位移还包含剪切和纵筋滑移等效应的贡献，为更合理地模拟墩顶力位移骨架曲线，等效塑性铰长度Lp采用文献[16]建议的计算公式（式（6））进行计算，以考虑剪切和纵筋滑移等效应。

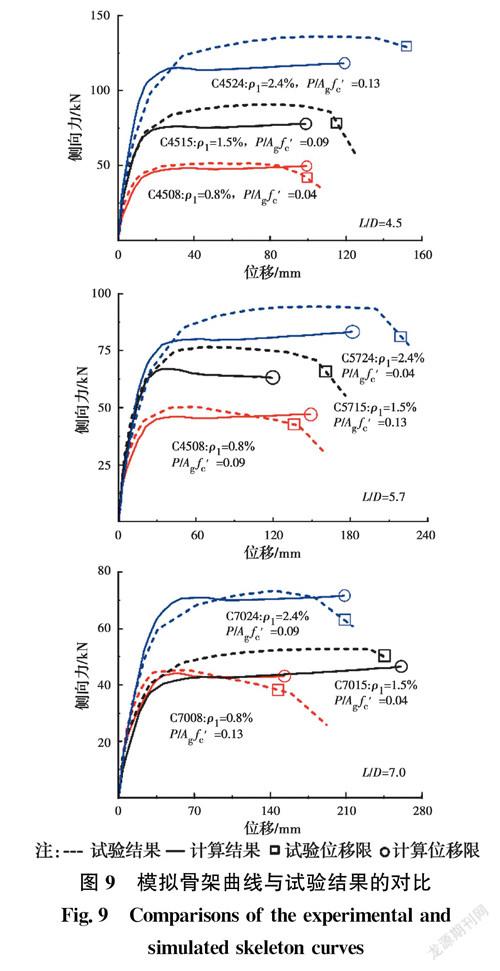
截面P-M-分析时，混凝土采用Concrete02模型[15]，纵筋采用Chang等[17]提出的等向强化钢筋模型，墩底截面曲率b及等效屈服曲率y按《规范》相关规定确定。图9给出了3组不同剪跨比桥墩的力位移骨架曲线计算值与试验值的对比，其中，试验骨架曲线取为正、负加载方向的均值;表3给出了截面层次墩顶极限位移、侧向最大荷载计算值与试验值的对比。9个试件墩顶极限位移计算值与试验值之比的均值为0.94;侧向最大荷载计算值与试验值之比的均值为0.91，最大误差在15%以内。

总体而言，截面层次数值模拟能较合理地预测不同剪跨比、纵筋率和轴压比桥墩的极限位移及最大承载力，且基本能体现力位移过程曲线。

4.2 构件层次

采用OpenSees集中塑性铰单元Beam-with Hinges Element[15]（以下简称为BHE）对桥墩墩顶力位移滞回曲线进行构件层次的模拟。BHE单元由Scott等[18]提出，基于有限单元柔度法建立，如图10所示，该单元假定非弹性变形集中在墩底塑性铰单元长度Lp内，而上部区段始终保持线弹性状态，概念与截面层次模拟的等效塑性铰模型一致。BHE单元的主要参数为塑性铰单元长度Lp和线弹性杆单元有效刚度EIeff，Lp按式（6）计算，有效刚度EIeff则采用文献[19]建议的计算公式（式（7））确定。式中EcIg为桥墩的毛截面弯曲刚度。

混凝土本构模型采用Scott等[18]修正后的Kent-Park模型，即OpenSees中的Concrete02，其应力应变滞回关系如图10所示。钢筋本构关系对桥墩滞回曲线的模拟有重要影响，选择合理的钢筋应力应变滞回模型是准确模拟钢筋混凝土桥墩非线性滞回性能的关键。

纵筋选用OpenSees中的ReinforcingSteel材料本构，该模型在等向强化钢筋模型基础上加入了低周疲劳效应，可以考虑钢筋的屈服流幅、等向强化、包晶格效应、低周疲劳效应（循环加载导致的强度、刚度退化以及钢筋断裂），其应力应变滞回关系如图10所示。ReinforcingSteel模型中，控制钢筋低周疲劳效应的3个参数为：损伤累积系数α、疲劳强度退化系数Cd、疲劳延性系数Cf，α、Cd控制强度、刚度退化，Cf控制钢筋断裂;Brown等[20]的钢筋低周疲劳材料试验得出的推荐值分别为：α=0.506、Cd=0.389、Cf=0.26。为考虑混凝土及箍筋约束对纵筋疲劳延性系数的影响，3个参数分别取为：α=0.506、Cd=0.389、Cf=0.22。针对C7024墩制作时墩底混凝土振捣欠密实，导致保护层及核心混凝土过早压溃、剥落，纵筋过早断裂的情况，分析时增加Cf取0.11的工况，以模拟纵筋提前断裂的现象。

图11给出了桥墩力位移滞回曲线计算结果与试验结果的对比，其中，C7024墩的计算结果为Cf取0.11的结果;Cf取0.22时，纵筋未出现断裂现象，与Cf取0.11的结果相比，仅是最大位移循環作用下未出现承载力下降而已。由图11可知，计算结果与试验结果吻合良好，表明所选取的BHE单元和材料本构能对桥墩的滞回曲线作出良好的模拟和预测，且能准确地模拟出钢筋混凝土桥墩在水平低周反复荷载作用下的捏拢效应、加卸载过程及强度刚度退化等滞回特性。在模拟过程中发现，桥墩承载力迅速降低时，通常对应纵筋的断裂，这与试验观察到的现象一致。ReinforcingSteel钢筋材料能准确模拟纵筋在循环荷载作用下的强度、刚度退化及断裂现象，是滞回曲线计算结果能较好体现桥墩在循环加载过程中强度、刚度退化的重要原因。

表3给出了构件层次墩顶极限位移、最大荷载计算结果与试验结果的对比。9个试件墩顶极限位移计算值与试验值之比的均值为1.07;最大荷载计算值与试验值之比的均值为0.98，最大误差在10%以内。因滞回模拟的加载历程与试验一致，纵筋强化效应亦相当，故侧向最大荷载计算值与试验值总体一致。需要说明的是，墩顶极限位移计算值的确定方法与试验值一致，仅力位移滞回曲线采用模拟结果;C4524墩及C7015墩在试验过程中均以纵筋断裂表示达到极限状态，侧向承载力均未下降到最大值的85%以下，故墩顶极限位移计算值与试验值一致，均为最大的加载位移值。

综上所述，选择合理的塑性铰长度Lp、有效刚度EIeff和材料本构模型，构件层次数值模拟能准确预测桥墩的力位移滞回曲线，且能合理估计相应的极限位移能力、侧向最大承载力，可作为钢筋混凝土桥墩抗震性能评估的有效方法，但其应用于足尺桥墩或实桥桥墩的效果仍有待检验。

5 方差分析

为考察墩高（剪跨比）、纵筋率、轴压比、配箍率等因素对极限位移、侧向最大荷载、极限状态累计耗能及等效屈服点有效弯曲刚度等抗震性能特征值的影响，进行正交试验方差分析。等效屈服点见图6圆圈位置，等效屈服点有效弯曲刚度定义为

式中：等效屈服力Vy及屈服位移Δy取为正、负加载方向的均值，EIeff具体结果见表2。

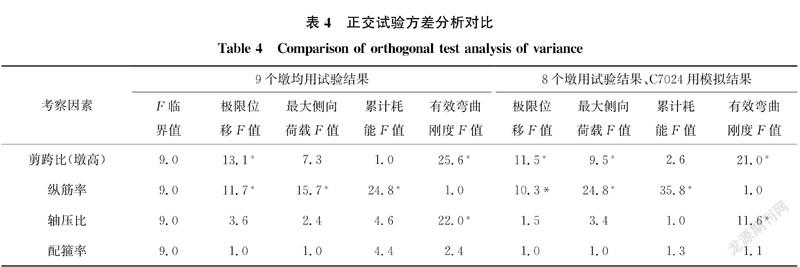
因设计的桥墩试验为四因素三水平正交无空列试验，且未做重复试验，故方差分析时需合理选择空列以进行误差估计。方差分析时，先计算各因素偏差平方和，然后选择偏差平方和最小者作为空列，再进行正交试验方差分析，被调整为空列的因素相应的F值为1.0。方差分析置信度取0.1，对应的F临界值为9.0，极限位移分析采用墩高为因素，其余采用剪跨比为因素。如抗震性能特征值的F值大于F临界值，则认为相应的因素对抗震性能特征值有显著影响。

表4给出了9个桥墩均采用试验值进行方差分析的结果，表中F值带“*”号者大于F临界值，表明相应的因素对抗震性能特征值有显著影响。因C7024墩墩底塑性铰区存在施工缺陷，导致保护层及核心混凝土过早压溃、剥落，纵筋过早断裂，未能获取其真实的抗震性能，故采用C7024墩的试验结果进行正交试验方差分析，有可能会得到失真的结果。鉴于OpenSees对各试验墩墩顶力位移滞回曲线均有良好的模拟效果，以C7024墩的模拟结果替代其试验结果，其余8个墩仍采用试验结果，再进行正交试验方差分析，以用于试验结果的对比、校验。OpenSees模拟时，纵筋疲劳延性系数Cf取0.22，通过增大墩顶侧向位移的方式使其达到极限状态，墩顶力位移滞回曲线模拟结果与试验结果的对比见图12。C7024墩模拟所得的极限位移、最大荷载、累计耗能及有效弯曲刚度分别为324.0 mm、79.5 kN、586 kN·m、13 276 kN·m2。

以C7024墩的模拟结果代替其试验结果后的方差分析结果，如表4所示。由表4可知，在置信度为0.1的水平下，9个墩均用试验结果和8个墩采用试验结果、C7024墩采用模拟结果两种情况的方差分析对各因素显著性检验的结果基本一致，后者增加了剪跨比对最大侧向力的显著性，说明C7024墩施工缺陷对各因素显著性检验的影响不明显。这一点亦可从C7024墩的位移延性系数达到5.3仍表现出良好的延性能力上得到一定印证。

正交试验方差分析结果表明：墩高、纵筋率对极限位移有显著影响，且随墩高、纵筋率的增大而增大;剪跨比、纵筋率对侧向最大荷载有显著影响，且随剪跨比的增大而减小，随纵筋率的增大而增大;纵筋率对极限状态累计耗能有显著影响，且随纵筋率的增大而增大;剪跨比、轴压比对等效屈服点有效弯曲刚度有显著影响，且随剪跨比、轴压比的增大而增大。这一结果可为参数识别、回归分析等相关研究提供试验层面的参考。

限于试验技术手段、试验样本数量及设计参数范围，上述结论推广至一般桥墩或实桥桥墩的普适性尚待进一步验证。

6 结论

进行了圆形钢筋混凝土桥墩的四因素三水平拟静力正交试验，并将试验结果与截面、构件两个层次的数值模拟结果进行对比分析，得出以下结论：

1）在考察的四因素三水平范围内，试验桥墩均具有良好的延性性能。位移延性系数和等效阻尼比的取值范围分别为5.3～8.4和0.19～0.29;即使对于塑性铰区存在一定施工缺陷的C7024墩，其延性系數仍处于较高水平。

2）在研究的参数范围内，方差分析表明：在置信度为0.1的水平下，墩高、纵筋率对极限位移有显著影响，且呈正相关关系;剪跨比、纵筋率对侧向最大荷载有显著影响，且与剪跨比呈负相关关系、与纵筋率呈正相关关系;纵筋率对极限状态累计耗能有显著影响，且呈正相关关系;剪跨比、轴压比对有效弯曲刚度有显著影响，且呈正相关关系。

3）截面和构件两个层次的数值模拟均与试验结果吻合良好。截面层次的数值模拟能较合理地预估不同剪跨比、纵筋率和轴压比试验桥墩的极限位移及最大承载力，可体现墩顶力位移过程曲线;构件层次的集中塑性铰单元能较准确地估算极限位移能力和极限承载力，较好地反映捏拢效应、强度与刚度退化等滞回特性。同时，应注意到集中塑性铰单元的建模与分析过程显示，等效塑性铰长度、有效刚度的取值合理性及钢筋滞回本构关系对模拟结果具有重要影响。

4）基于等效塑性铰模型的截面及构件层次的数值模拟均可作为钢筋混凝土桥墩抗震性能评估的有效方法，但其应用于足尺桥墩或实桥桥墩的有效性有待进一步研究。

参考文献：

[1] Seismic design criteria： Caltrans-V1.7 [S]. Sacramento： California Department of Transportation， 2013.

[2] Guide specifications for LRFD seismic bridge design： AASHTO-2015[S]. Washington： American Association of State Highway and Transportation Officials， 2015.

[3] Design provisions for earthquake resistance of structures-Part 2： Bridges： Eurocode 8-2005 [S]. Brussels： Committee European De Normalization， 2005.

[4] Design specifications for highway bridges， Part V： Seismic design： JRA-2002 [S]. Tokyo： Japan Road Association， 2002.

[5] 公路桥梁抗震设计规范： JTG/T 2231-01—2020 [S]. 北京：人民交通出版社， 2020.

Guidelines for seismic design of highway bridges： JTG/T B02-01-2020 [S]. Beijing： China Communications Press， 2020. （in Chinese）

[6] 公路工程抗震设计规范： JT 004—89 [S]. 北京：人民交通出版社， 1989.

Specifications earthquake resistant design for highway engineering：JT004-89 [S]. Beijing： China Communications Press， 1989. （in Chinese）

[7] LEHMAN D， MOEHLE J， MAHIN S， et al. Experimental evaluation of the seismic performance of reinforced concrete bridge columns [J]. Journal of Structural Engineering， 2004， 130（6）： 869-879.

[8] 王君杰， 苏俊省， 王文彪， 等. 配置HRB500E， HRB600钢筋的混凝土圆柱抗震性能试验[J]. 中国公路学报， 2015， 28（5）： 93-100， 107.

WANG J J， SU J S， WANG W B， et al. Experiment on seismic performance of circular concrete columns reinforced with HRB500E， HRB600 steel [J]. China Journal of Highway and Transport， 2015， 28（5）： 93-100， 107. （in Chinese）

[9] TREJO D， LINK T B， BARBOSA A R. Effect of reinforcement grade and ratio on seismic performance of reinforced concrete columns [J]. ACI Structural Journal， 2016， 113（5）： 907-916.

[10] BARBOSA A R， LINK T， TREJO D. Seismic performance of high-strength steel RC bridge columns [J]. Journal of Bridge Engineering， 2016， 21（2）： 04015044.

[11] BARCLEY L， KOWALSKY M. Seismic performance of circular concrete columns reinforced with high-strength steel [J]. Journal of Structural Engineering， 2020， 146（2）： 04019198.

[12] SU J S， LI Z X， WANG J J， et al. Numerical simulation and damage analysis of RC bridge piers reinforced with varying yield strength steel reinforcement [J]. Soil Dynamics and Earthquake Engineering， 2020， 130： 106007.

[13] 成虎， 李宏男， 王东升， 等. 考虑锈蚀黏结退化的钢筋混凝土桥墩抗震性能分析[J]. 工程力学， 2017， 34（12）： 48-58.

CHENG H， LI H N， WANG D S， et al. Seismic performance analysis of reinforced concrete bridge column considering bond deterioration caused by chloride ion induced corrosion [J]. Engineering Mechanics， 2017， 34（12）： 48-58. （in Chinese）

[14] PARK R. Evaluation of ductility of structures and structural assemblages from laboratory testing [J]. Bulletin of the New Zealand Society for Earthquake Engineering， 1989， 22（3）： 155-166.

[15] MAZZONI S， MCKENNA F， FENVES G L. Open system for earthquake engineering simulation user manual [Z/OL]. http：// www.opensees.berkeley.edu.

[16] 李贵乾， 唐光武， 郑罡. 圆形钢筋混凝土桥墩等效塑性铰长度[J]. 土木工程学报， 2016， 49（2）： 87-97.

LI G Q， TANG G W， ZHENG G. Equivalent plastic hinge length of circular reinforced concrete bridge columns [J]. China Civil Engineering Journal， 2016， 49（2）： 87-97. （in Chinese）

[17] CHANG G A， MANDER J B. Seismic energy based fatigue damage analysis of bridge piers： Part I-evaluation of seismic capacity [R]. New York： Multidisciplinary Center for Earthquake Engineering Research， 1994.

[18] SCOTT M H， FENVES G L. Plastic hinge integration methods for force-based beam-column elements [J]. Journal of Structural Engineering， 2006， 132（2）： 244-252.

[19] 鄭罡， 李贵乾. 钢筋混凝土桥墩有效刚度[J]. 土木工程学报， 2013， 46（6）： 44-52.

ZHENG G， LI G Q. Effective stiffness of reinforced concrete bridge piers [J]. China Civil Engineering Journal， 2013， 46（6）： 44-52. （in Chinese）

[20] BROWN J， KUNNATH S K. Low cycle fatigue behavior of longitudinal reinforcement in reinforced concrete bridge piers [R]. New York： Multidisciplinary Center for Earthquake Engineering Research， 2000.

（编辑 黄廷）

收稿日期：2021-07-09

基金项目：国家自然科学基金（51978112）

作者简介：李贵乾（1984- ），男，高级工程师，主要从事桥梁结构设计及桥梁抗震性能研究，E-mail：273738890@qq.com。

郑罡（通信作者），男，博士，研究员，博士生导师，E-mail：1156039428@qq.com。

Received：2021-07-09

Foundation item：National Natural Science Foundation of China （No.51978112）

Author brief：LI Guiqian （1984- ）， senior engineer， main research interests： structural design and seismic performance of bridge， E-mail： 273738890@qq.com.

ZHENG Gang （corresponding author）， PhD， researcher， doctorial supervisor， E-mail： 1156039428@qq.com.