岩土材料的基因特征及其测试方法

刘东升　刘汉龙　吴越　仉文岗

摘 要：由于岩土材料固有的天然成因，其基本物理力学特性表现出不同程度的空间变异性。基于有限的检测数据很难对岩土材料的整体物理力学特征进行描述，而特征参数取值的差异对岩土工程稳定状态的判别和相关工程设计结果的影响不可忽略。基于该问题，提出对一定空间范围内的特定岩（土）性材料性质整体特性进行描述的岩土材料基因特征的概念，给出基因特征的定义及其基本属性，提出运用大数据理论对大量实际工程中检测到的岩土材料参数数据进行统计分析并寻找其基因特征的思路。研发了岩土材料基因特征大数据管理及分析软件系统，实现了对岩土材料大数据实施收集、传输、分类、筛选、管理和统计分析的功能，并结合在重庆地区收集到的7万余条典型岩土材料数据，对该地区的典型岩土材料基因特征进行分析，得到相应的基因图谱。

关键词：岩土材料;基因特征;大数据;统计分析;贝叶斯估计

中图分类号：TU411;TU413 文献标志码：A 文章编号：2096-6717（2022）04-0001-09

Genetic features of geo-materials and their testing method

LIU Dongsheng1， LIU Hanlong2， WU Yue1，3， ZHANG Wengang2

（1. Chongqing Bureau of Geological Survey and Mineral Exploration， Chongqing 401121， P. R. China; 2. School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China; 3. School of Civil Engineering and Architecture， Chongqing University of Science and Technology， Chongqing 401331， P. R. China）

Abstract： Basic features of geo-materials generally show spatial variability to some extent due to their natural cause of formation. Its difficult to give a full description of the field basic features of geo-materials by use of limited testing data. The values of parameters which represent the basic features of geo-materials have great influence on the geotechnical engineering design. In this paper， a concept of genetic features for geo-materials is firstly proposed and definition as well as some attributes with regards to this concept are also given. Based on big data analysis and a large amount of data collected from practical projects in Chongqing， method for searching the genetic features of geo-materials is proposed. A software about the genetic feature analysis is developed and it can be used for collection， analysis and management of geo-materials data obtained from engineering practice. Based on it， more than 70 000 data about genetic features of typical geo-materials in Chongqing are collected and analyzed， some typical genetic maps of geo-materials in Chongqing are obtained.

Keywords：geo-material; genetic feature; big data; statistical analysis; Bayes estimation

随着科学技术的不断发展，岩土力学的各种计算理论和分析模型已日臻完善，计算方法和分析手段也多种多样，许多先进的理论和方法已成功运用到实际工程中，为解决岩土工程实际问题提供了有力的理论基础和技术支撑，极大地推动和促进了岩土工程学科和工程实践的发展[1-2]。然而，一个十分关键的因素仍制约着一些先进岩土力学理论在实际工程中的应用，阻碍了岩土工程的快速发展，这个因素就是对岩土材料基本物理力学特征的认识，具体而言就是对岩土材料基本物理力学参数的正确确定。任何岩土力学理论和方法的应用都必须建立在对岩土材料基本物理力学参数的正确认识和准确识别之上，否则，任何先进的理论和精确的计算，其结果都会出现失真或谬误，从而使理论研究和数值计算的结果变得毫无意义[3]。而由于岩土材料自身固有的特殊成因，其物理力学性质表现出较为显著的空间随机变异性和不确定性，加之岩土工程问题涉及的空间区域往往比较大，正确评价一定区域不同岩（土）性材料的物理力学特征、获取一定空间区域范围内岩土材料真实可靠的物理力学参数是一项十分重要但又相当困难的工作。目前，工程界常用的做法是，在工程勘查过程中获取几个试验点岩土材料样本的试验值，经过简单的统计分析后，提出反映该岩土材料整体性质的物理力学参数，并用于指导工程设计。由于试验样本的局限性，这种方法存在较大的缺陷和不足，使得人们对所获取的参数的真实性、可靠性和代表性表示怀疑。因此，勘查设计人员出于保守的设计观念及本能的自我保护意识，对测得的强度参数会进行不同程度的折减，然后再提供给工程设计或评估使用。折减的目的是人为考虑岩土材料参数的变异性和参数测试过程中可能带来的误差，这样的做法显然具有极大的主观随意性，缺乏必要的科学依据。材料参数是工程设计的基础和核心，参数选择的不合理会增加工程事故的風险或增加工程建设的投资，对工程项目的安全性和经济性带来不利影响。由此可见，对岩土材料的基本物理力学特征进行研究非常必要。AF9DA212-F27C-48ED-B9D1-A092D886E1D4

很多高等院校和科研机构都有先进的岩土材料基本力学特性研究设备，也有很多专家在利用这些设备从事岩土材料基本物理力学特征的研究，研究也很深入，并取得了很多成果[3-18]。但由于受到试验样本数量的限制，其研究结果是否具有对某种岩土材料整体区域特征的代表性和普适性依然有待进一步确认，同时，也缺乏相应的对比验证，这是有关岩土材料参数特征“点估计”和“区域估计”之间的关系问题。“点估计”的结果对局部小区域特征的揭示效果十分明显，但岩土体具有比较显著的空间变异性，“点估计”与“区域估计”结果之间有区别，特别是在“点估计”样本数量偏少的情况下，差别更明显，不可完全取而代之。

根据岩土材料物理力学特征固有的空间变异性和不确定性特征，结合岩土材料在不同区域的地质成因和构造条件，提出“岩土材料基因特征”的概念，用以描述岩土材料在一定区域上的基本物理力学特征，旨在运用数据统计的方法寻找一定空间区域范围内特定岩土材料群组（岩土材料岩性类别）的共性——基本物理力学特征，建立相应的岩土材料基本参数数据库，运用大数据分析方法对其进行基因特征识别和提取，并根据不断补充的测试数据对数据库进行补充完善，逐步修正其基因特征，使之对基因特征的描述逐步趋于准确，并反过来指导参数取值，为岩土力学理论应用和岩土工程设计提供可靠的基础数据。

1 岩土材料基因特征的概念

“基因”一词源于生物学，是指存在于生物种群内部具有遗传因子的基础物质。基因的作用体现在两个方面，一是传递遗传信息，二是决定生物的行为特征和健康状况。每一个生物都具有自己的基因特征，而每一个生物种群也具有该种群共有的基因共性（如人类、鱼类、鸟类、爬行动物以及各种植物种群等），这些基因共性对研究该种群的生物衍变和个性特征具有重要意义。

同理，尽管岩土介质为非生物类物质，但也具有内部微观材料及其组织结构特征，微观细颗粒和其他介质经过数以亿年的物理化学作用，形成了今天的岩土材料。特定的材料物质组分，特定的结构方式，特定的温度、压力等生成环境影响因素赋予了该岩土材料群组特定的基因特性，并以特定的物理力学特征表现出来。尽管从工程建设的角度探求岩土材料基因的遗传特性意义不大，但从研究一定区域范围内相同岩土材料群组表现出来的物理力学特征上讲，岩土材料基因特征的研究不仅具有重要的理论意义，而且具有重要的工程适用价值。

岩土材料基因特征的定义可以表述为：在一定空间区域内，同一岩土材料群组所具有的共性基本物理力学特征。基于该定义，岩土材料基因特征应该具备如下属性：

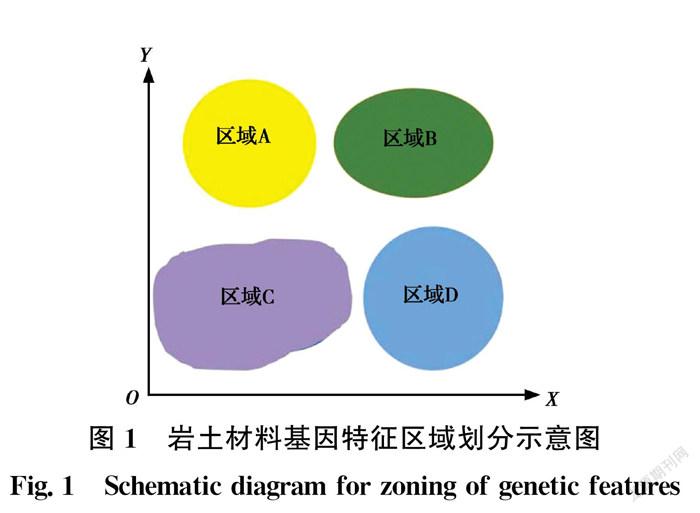
1）区域性：由于受到岩土材料成因的影响，只有在基本相同的条件下形成的同一类岩土材料才具备相同或类似的基因特质;不同地区的岩土材料，由于其成因条件不同，表现出来的基因特征也有较大区别，由此决定了基因特征的区域性（图1）。

2）群组性：不同岩（土）性的岩土材料由于微观组分材料不同，结构方式不同，生成环境不同，具有不同的基因特征，因此，在对其进行研究时必须加以区分，不能相互混淆（图2）。

3）趋同性：同一区域相同群组的基因特征是指其具有代表性的共性或趋同特征，是一种统计概念，不排除在个别点上样本指标表现出细小差异。因此，基因特征的识别或检测必须要有足够数量的样本数据为基础，通过统计分析得出具有代表性的共性特征指标。

需要特别指出的是，岩土材料基本物理力学参数试验是岩土基因检测的基本方法，但每一个试验结果本身不能作为该群组基因特征描述的唯一指标，岩土材料基因特征和基本物理力学参数试验结果之间是群体与个体、一般性与特殊性的关系，只有通过对大量个体结果的统计分析，才能找到群体的共性化特征。

2 岩土材料基因特征研究的作用和意义

学者们已经对岩土材料基本物理力学特性进行了大量的研究，也取得了丰富的成果。但是，这些研究成果大多表现为对某一个特定工程的某一种特定岩土材料的某一个特定参数指标的研究，如强度指标、变形指标、渗透指标或时效性指标等，缺乏系统性和规范性，特别是研究结果只是针对特定空间点上的样本开展，结果缺乏在相关群组或空间区域上的参考价值和推广应用意义，也制约了这些研究结果价值的进一步体现。而岩土材料基因特征的概念则从广义上涵盖了岩土材料的各种基本内在属性特征，从描述上更加统一和规范，更重要的是这一概念不仅包含而且拓展了传统岩土材料基本物理力学性质研究的内涵，是一种基于传统试验研究结果基础之上的宏观统计结果，体现的是一定区域内相同群组岩土材料的宏观性质特征。点上获取的试验数据既是区域统计的数据源，又是对既有基因特征统计结果的修订和补充信息;而既有的基因特征又可以对每一次检测所得的数据进行校验和比较，一些奇异数据的出现促使人们去分析查找原因，避免检测试验过程中出現人为错误或系统误差，保证数据的可靠性和真实性。岩土材料基因特征研究的意义在于，目前还不能非常准确地定量描述一定区域范围内岩土材料的基本物理力学性质的整体特征，仅仅通过有限的几个点上测得的数据去表征一个区域的岩土材料特性未免有失偏颇，有盲人摸象的感觉。因此，基于特定条件下相关大数据统计分析得到的结果从概率的角度上讲有可能比具体试验得到的某些数据更可靠，也更能代表岩土材料的区域物理力学特性。由于岩土材料均为天然形成，与混凝土、钢材等人工合成材料不同，其测试数据变异性相对较大，点上测得的数据对区域的代表性显得相对较低，这就使得基于区域统计分析的岩土材料基因特征的研究意义变得十分重要。

岩土材料基因特征的研究可以全面系统地对不同空间区域内不同岩（土）性群组的基本基因进行分析，建立相应的基因数据库，绘制相应的基因图谱，从而系统全面地分析各种基因元素对岩土材料物理力学特征的影响，分析这种影响的敏感性和相关性，根据分析结果，结合工程实际，需要对这些基因元素进行改良和干扰，提高这些岩土材料在某些方面的性能，以满足工程建设的需要，可以把这项工作称为岩土材料基因改良或转变。实际上，目前工程中广泛使用的地基处理中的各种物理化学加固技术以及生物岩土材料的研究都可以归结为对岩土材料基因特征的改良和转变。AF9DA212-F27C-48ED-B9D1-A092D886E1D4

3 岩土材料基因特征的测定方法

岩土材料基因特征的测定方法并不复杂，原理也比较简单，就是利用现有的岩土材料基本物理力学参数测试仪器进行各种基本参数的测试，包括室内测试和现场测试。测试内容包括不同地区不同群组岩土材料的物质组分、结构方式以及物理力学特征参数等。问题的关键和难点在于，必须要有足够数量的测试数据，才能对某一群组岩土体的基因特征进行统计分析，并揭示其基因特征值。由于测试样本的获取和制作需要进行钻孔、取样、制样和试验等复杂工作，每一个试验样本数据的获取都需要付出较大的经济成本和人工代价，加之许多样本需要做破坏性试验，样本不可重复使用，当数据样本需求量较大时，需要的研究经费和人力成本都比较高，这就使得这项工作实施起来十分困难。

然而，一个被忽略的现象是，中国每年都在不同地区进行着数量巨大的工程建设，工程建设一定离不开对建设场地的地质评价（如地基承载力、变形特性、稳定性等），要完成这些评价就必须完成大量的场地勘查工作，提供相应的岩土材料物理力学参数以满足设计需要。令人惋惜的是，这些海量的数据在项目实施完成后便被束之高阁。单独从一个工程项目的角度上看，项目完成后，这些数据确实不再具有使用的价值，但从研究岩土材料基因特征的角度上看，这些数据就异常珍贵。如果能把这些海量数据收集起来，按地理区域、地层构造、岩土群组、基因元素等因素进行分类整理，并按照大数据方法进行统计分析，有可能得到特定岩土材料群组的基因特征。事实上，目前的情况是，数据是客观存在的，样本是大量的，需要完成的工作就是通过适当的技术手段收集数据，按照科学的方法分类数据，运用数学的方法统计分析数据，提取相应的岩土材料基因特征，并用于相同群组岩土材料设计参数的选取参照，服务工程建设。特别需要强调的是，岩土材料参数的获取和更新是一个动态的过程，每年都会有大量的数据补充到相应的数据库，并不断对原有岩土材料参数基因特征进行逐步修订。可以想象，经过数年或者数十年的数据积累，不同区域各个岩土材料群组的基因特征就越来越清晰，也越来越准确，对工程建设安全性和经济性的影响也将越来越明显。互联网技术的产生和大数据技术的出现使得数据的获取和统计变得十分方便，关键是如何运用到岩土基因特征的分析中。岩土材料基因特征的分析方法很简单，就是收集数据、分类数据、分析数据、提取特征值，技术路线如图3所示。为了使数据的分析更加合理和可靠，在统计过程中可以使用贝叶斯参数估计等方法，提高数据估计的效率和精度。

4 重庆市岩土材料基因特征研究

重慶是著名的山城，具有显著的地形地貌特征和地质构造特点，地层岩性也具有显著的地区特色。重庆市地质矿产勘查开发局所属的地勘队伍数十年来长期从事全市的地质勘查工作，承接了数以万计的各类工程建设和地质灾害防治项目的勘查、设计和施工，积累了大量的岩土材料物理力学参数数据，为该地区岩土材料基因特征的研究创造了良好的条件。

4.1 建立岩土材料数据采集及分析管理系统

基于全局的多个岩土材料测试中心，利用互联网技术，建立了一套“岩土材料数据采集及分析管理系统”。该系统可以对不同数据采集点的检测数据进行实时采集、传输、分类、筛选、管理和统计分析，并运用贝叶斯理论，结合历史数据特征和现场检测结果对具体项目的参数值进行估计。目前，已经采集了近3年来重庆地区测试到的各类岩土材料物理力学参数数据7万余条，对每一个数据的基本特征进行描述，存入相应的数据库，以备大数据统计分析。数据分析管理系统技术路线如图4所示。

4.2 运用数理统计方法对基因特征进行分析

根据系统设置的相关条件对数据库里的数据按区域、群组以及岩（土）性和物理力学指标进行分类、筛选，提取符合条件的有效数据进行统计分析，得到已有数据的基本物理力学特征或基因特征，并以此作为岩土材料基因特征估计的先验信息。

图5～图8是重庆渝中区两个强度指标的直方图以及重庆部分区县砂岩、泥岩单轴抗压强度的基因特征图谱。由图5可知，渝中区泥岩天然单轴抗压强度呈左偏态分布。而在图6中，渝中区砂岩天然单轴抗压强度则呈右偏态分布。由图7可知，重庆市各区县泥岩天然抗压强度总体呈渝东北地区偏高而渝西南、渝东南偏低的规律。由图8可知，重庆市各区县砂岩天然抗压强度总体呈渝东北地区偏低而渝西南偏高的规律，特殊点在于渝东南的秀山。此外，酉阳、彭水、巫溪县缺少相关数据支撑，需进一步用数据核实确定。

4.3 贝叶斯估计获取岩土材料设计参数

为了同时考虑历史数据基因特征值和现场检测数据对参数取值的影响，使用贝叶斯估计方法对岩土材料的参数进行了估计。对于某特定工程项目，以系统分析提供的该地区特定岩土材料群组的历史基因特征值为先验参数特征，以项目实际试验值作为后验参数特征，运用贝叶斯估计方法，通过计算估计出用于工程设计的岩土参数设计值。

工程实践表明，岩土强度参数多服从正态或对数正态分布[19]，对于服从正态分布的岩土强度参数，即x～N（μ，σ2），其中，x表示岩土强度参数，（μ，σ2）为强度参数服从的正态分布的均值和方差。（μ，σ2）全面地反映了岩土强度参数的随机分布特征，即岩土强度参数基因特征。对于一个具体工程，强度参数黏聚力c和内摩擦角φ对应的（μ，σ2）是未知的，如何科学地确定（μ，σ2）成为岩土强度参数取值是否合理的关键。传统的做法是根据有限的现场抽样实验结果进行统计，采用“点估计”的方法来推断（μ，σ2），采用现场样本的均值为总体均值μ的无偏点估计量，现场样本的方差为总体方差σ2的无偏点估计量，即

式中：x为岩土强度指标样本均值;s2为岩土强度指标样本方差;为总体均值μ的点估计量;2为方差σ2的无偏点估计量。

由于取样条件及勘察成本的限制，现场样本数量往往十分有限，多数工程通常只有3～6组，这属于统计学中的小样本，从而使得由式（1）确定的岩土强度参数特征与岩体实际的基因特征存在不同程度的差异。AF9DA212-F27C-48ED-B9D1-A092D886E1D4

为此，基于贝叶斯统计理论提出μ、σ2服从一个二维的联合先验分布，表示为

式中：π（μ，σ2）为（μ，σ2）的联合先验分布;π（σ2）为σ2的先验分布;π（μ|σ2）为σ2条件下μ的先验分布，并认为μ|σ2和σ2分别服从正态分布和逆伽马分布，即

式中：μ0、κ0、υ0、σ20为待确定的超参数。

称（μ，σ2）的先验分布为正态逆伽马分布。在先验分布的基础上，根据贝叶斯公式，可以得到在现场样本数据条件下（μ，σ2）的后验分布，按照共轭先验的理论，先验分布与后验分布属于同族分布，即

式中：μn=κ0κ0+nμ0+nκ0+nx;κn=κ0+n;υn=υ0+n;υnσ2n=υ0σ20+（n-1）s2+κ0nκ0+n（μ0-x）2;π（μ，σ2|x）为（μ，σ2）的后验分布;x为现场样本均值;s2为现场样本方差;n为现场样本数量。

采用最大后验估计作为参数的估计量，（μ，σ2）的最大后验估计为

式中：μMD、σ2MD为（μ，σ2）的最大后验估计量;μ0、κ0、υ0、σ20为先验分布超参数，由历史数据确定。

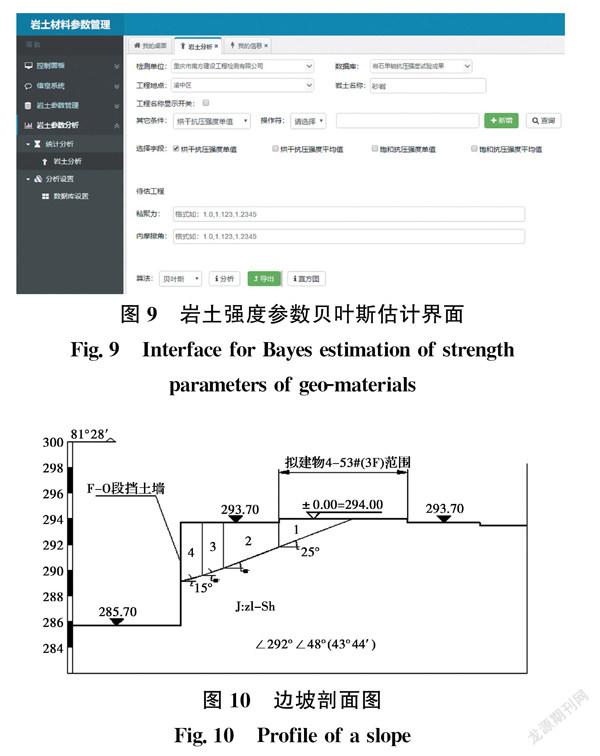
利用式（6）可将历史数据的基因特征与现场数据进行科学的综合，得到更为合理的岩土强度参数随机分布特征参数的估计值。以此算法为基础，在岩土大数据分析管理软件平台上实现了岩土强度參数的贝叶斯估计，如图9所示。

4.4 基于贝叶斯参数估计的工程案例

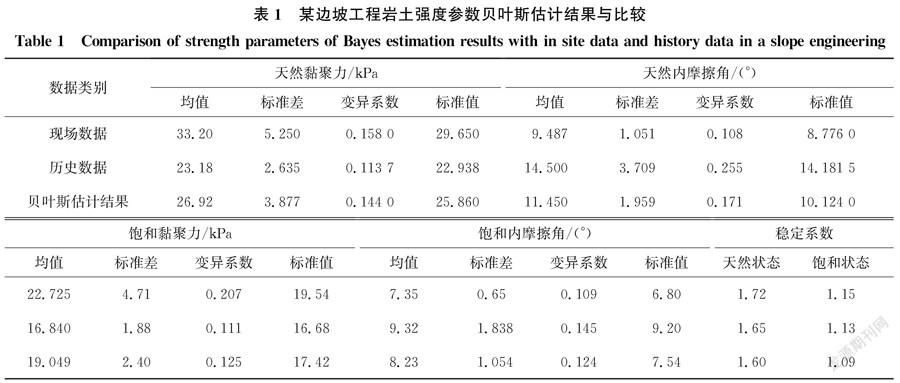
利用该方法对重庆市某边坡工程的岩土强度参数进行估计，并对不同算法参数估计结果进行对比分析。边坡剖面如图10所示，坡体为粉质黏土。估计结果如表1和图11、图12所示。

表1为该工程岩土强度参数c、在天然和饱和两种状态下的历史基因特征、现场检测数据以及贝叶斯估计的结果，同时，表中还根据三者各自的参数特征算出了相应的边坡稳定性系数。

图11和图12是岩土强度参数c、分别在天然和饱和状态下3种统计方法所得到的取值柱状图。

由表1和图11、图12可见，贝叶斯估计的结果对历史基因特征和现场实测结果均有不同程度的修正，其修正幅度的大小与历史基因特征值和现场实测数据值的变异系数有关，表明岩土材料基因特征对实际工程参数取值的影响不可忽略。贝叶斯估计的参数标准值可能增加或降低历史基因特征和现场实测数据的标准值，但通常情况下，贝叶斯估计的结果总是位于历史基因特征和现场实测数据标准值之间，这一结果也充分表明了贝叶斯估计方法的合理性和正确性。随着历史样本数量的不断增加，历史数据基因特征值与现场实测数据特征值之间的差距就会逐步减小，基于这些数据的贝叶斯估计结果也会与二者的结果逐步趋近，从而实现对岩土材料整体基因特征的正确描述。

需要特别指出的是，一旦使用了贝叶斯参数估计值，强度参数取值的变化必然导致边坡抗滑力的计算结果随之发生变化，对边坡稳定状态的判断也会出现不同的结果。稳定性状态的判定不仅与不同强度参数变化的幅度有关，还与不同强度参数对稳定性影响的敏感性有关，因此，实际稳定状态评价的变化必须通过对具体的边坡稳定性计算分析得到，不能根据参数变化情况直接评估。

从概率的角度上讲，由于现场测试数据样本量少，统计结果可信度相对较低;同时，考虑工程周边相邻工程参数历史基因特征和工程现场测试数据的贝叶斯估计方法更科学合理。

5 结论与建议

1）借用生物学基因的概念，提出了岩土材料基因特征的概念，并给出了相应的属性。用岩土材料基因特征描述一定几何空间范围内相同群组岩土材料的基本物理力学特性对具有不确定性和空间变异性的岩土材料基本性质的描述更加规范和科学。

2）分析了岩土材料物理力学参数具体点的测试结果与该区域范围内相应的基因特征值之间的相互关系，具体测试结果只能代表岩土材料在区域内有限样本点上的“点估计”，不能完全代表岩土材料的区域整体属性;基因特征是大量这类样本经过统计分析得出的遵从特定分布的特征值，随着样本数量的不断增加，基因特征对岩土体基本属性的描述将越来越准确。

3）提出运用大量已有实际工程检测数据对岩土材料基因特征进行统计分析的设想，并运用互联网技术和大数据分析方法建立了相应的数据收集、传输、分类、筛选、管理和分析软件平台，结合收集到的7万多条重庆地区的实际检测数据，对该地区典型岩土材料的物理力学基因特征进行分析，得到了该地区初步的基因特征图谱。

4）根据统计得到的重庆典型岩土材料基因图谱，并结合某具体滑坡工程实例检测所得到的检测数据，运用贝叶斯估计理论对实际工程的岩土材料强度参数进行估计。结果表明，基于贝叶斯估计的参数估计值与仅使用历史基因特征或仅使用现场实测数据所得到的参数估计值之间存在一定的差异，贝叶斯估计值通常位于历史基因特征值和现场实测数据特征值之间，随着数据样本的不断增加，3种方法估计的参数值将逐步趋于一致。

笔者提出的是一种以大量实际工程检测数据为依托，运用大数据统计寻找岩土材料基因特征的方法，因此，数据本身的数量和质量都十分关键。鉴于当前岩土材料检测单位和项目勘查单位之间的职责界限，加之检测报告的服务对象仅为某一特定的具体工程，检测单位在检测报告中对样本属性的描述还不是十分完善，因此，在一定程度上影响了统计样本的分类提取，也影响了基因特征的提取质量。建议国家或各省市或行业部门对岩土材料工程参数的检测报告格式进行规范，提出统一的报告模板和岩土数据结构，其中尽可能对测试参数的相关属性进行详细描述，从而提高参数用于大数据分析时的实用性和针对性，确保分析所得岩土材料基因特征的准确性和可靠性。参考文献：

[1] 陈祖煜. 土质边坡稳定性分析——原理·方法·程序 [M].北京： 中国水利水电出版社， 2003.

CHEN Z Y. Soil slope stability analysis： Theory， methods and programs [M]. Beijing： China Water & Power Press， 2003. （in Chinese）AF9DA212-F27C-48ED-B9D1-A092D886E1D4

[2] 陈祖煜. 岩质边坡稳定性分析——原理·方法·程序[M].北京： 中国水利水电出版社， 2005.

CHEN Z Y. Rock slope stability analysis： Theory， methods and programs [M]. Beijing： China Water & Power Press， 2005. （in Chinese）

[3] JUANG C H， CARRANZA-TORRES C， CROSTA G， et al. Engineering geology： A fifty year perspective [J]. Engineering Geology， 2016， 201： 67-70.

[4] 张继周， 缪林昌， 刘峰. 岩土参数的不确定性及其统计方法[J]. 岩土力学， 2008， 29（Sup1）： 495-499.

ZHANG J Z， MIAO L C， LIU F. Uncertainties of soil properties and its statistical methods [J]. Rock and Soil Mechanics， 2008， 29（Sup1）： 495-499. （in Chinese）

[5] 曾晟， 徐华清， 张佳男， 等. 岩土工程参数Bayes法推断中先验与后验样本大小的探讨[J]. 南华大学学报（自然科学版）， 2015， 29（3）： 30-33.

ZENG S， XU H Q， ZHANG J N， et al. Discussion of priori and posteriori samples number of the geotechnical parameters with the Bayes inference method [J]. Journal of University of South China （Science and Technology）， 2015， 29（3）： 30-33. （in Chinese）

[6] 张蕾， 唐小松， 李典庆， 等. 基于Copula函数的岩土结构物系统可靠度分析[J]. 岩土力学， 2016， 37（1）： 193-202.

ZHANG L， TANG X S， LI D Q， et al. System reliability analysis of geotechnical structures based on the Copula function [J]. Rock and Soil Mechanics， 2016， 37（1）： 193-202. （in Chinese）

[7] KELLY R， HUANG J S. Bayesian updating for one-dimensional consolidation measurements [J]. Canadian Geotechnical Journal， 2015， 52（9）： 1318-1330.

[8] 王新， 黄磊群. 随机加权法辅助小样本岩土参数概率分布的边坡稳定性分析[J]. 公路工程， 2017， 42（3）： 131-136.

WANG X， HUANG L Q. Analysis of slope stability based on probability distribution of small sample geotechnical parameters by random weighting method [J]. Highway Engineering， 2017， 42（3）： 131-136. （in Chinese）

[9] 蒋水华， 魏博文， 黄勁松. 考虑参数空间变异性的失稳边坡参数概率反分析[J]. 岩土工程学报， 2017， 39（3）： 475-485.

JIANG S H， WEI B W， HUANG J S. Probabilistic back analysis of slope failure considering spatial variability of soil properties [J]. Chinese Journal of Geotechnical Engineering， 2017， 39（3）： 475-485. （in Chinese）

[10] 肖欣， 章杨松. 基于贝叶斯网的岩体抗剪强度区间概率分析[J]. 勘察科学技术， 2016（2）： 5-10， 26.

XIAO X， ZHANG Y S. Interval probability analysis of rock mass shear strength based on Bayesian network [J]. Site Investigation Science and Technology， 2016（2）： 5-10， 26. （in Chinese）

[11] GOHARZAY M， NOORZAD A， ARDAKANI A M， et al. A worldwide SPT-based soil liquefaction triggering analysis utilizing gene expression programming and Bayesian probabilistic method [J]. Journal of Rock Mechanics and Geotechnical Engineering， 2017， 9（4）： 683-693.AF9DA212-F27C-48ED-B9D1-A092D886E1D4

[12] CONTRERAS L F， BROWN E T， RUEST M. Bayesian data analysis to quantify the uncertainty of intact rock strength [J]. Journal of Rock Mechanics and Geotechnical Engineering， 2018， 10（1）： 11-31.

[13] 赵宇飞， 汪小刚， 杨健. 基于二维正态分布的岩土参数Bayes方法优化[J]. 中国水利水电科学研究院学报， 2006， 4（2）： 93-96.

ZHAO Y F， WANG X G， YANG J. Bayes method of optimizing geotechnical parameters based on two-dimension normal distribution [J]. Journal of China Institute of Water Resources and Hydropower Research， 2006， 4（2）： 93-96. （in Chinese）

[14] 李红英， 谭跃虎， 赵辉. 某滑坡体岩土参数概率分布统计分析方法研究[J]. 地下空间与工程学报， 2012， 8（3）： 659-665.

LI H Y， TAN Y H， ZHAO H. The statistical analysis technique research on probability distribution of geotechnical parameters of one landslide [J]. Chinese Journal of Underground Space and Engineering， 2012， 8（3）： 659-665. （in Chinese）

[15] 胡记磊， 唐小微， 裘江南. 基于贝叶斯网络的地震液化概率预测分析[J]. 岩土力学， 2016， 37（6）： 1745-1752.

HU J L， TANG X W， QIU J N. Prediction of probability of seismic-induced liquefaction based on Bayesian network [J]. Rock and Soil Mechanics， 2016， 37（6）： 1745-1752. （in Chinese）

[16] 程圣国， 方坤河， 罗先启， 等. 三峡库区新生型滑坡滑带土抗剪强度确定概率方法[J]. 岩石力学与工程学报， 2007， 26（4）： 840-845.

CHENG S G， FANG K H， LUO X Q， et al. Probability method to determine shear strength of slide zone clay for neogenic landslide in Three Gorges Reservoir area [J]. Chinese Journal of Rock Mechanics and Engineering， 2007， 26（4）： 840-845. （in Chinese）

[17] 工程結构可靠性设计统一标准： GB 50153—2008 [S]. 北京： 中国计划出版社， 2009.

Unified standard for reliability design of engineering structures： GB 50153-2008 [S]. Beijing： China Planning Press， 2009. （in Chinese）

[18] ANDREW G， JOHN B， CARLIN H S. Bayesian data analysis [M]. 3rd Edition. New York： CRC Press， 2013.

[19] 岩土工程勘察规范： DGJ 08-37—2002 [S]. 北京：中国建筑工业出版社， 2009.

Code for investigation of getechnical engineering： DGJ 08-37-2002 [S]. Beijing： China Architecture & Building Press， 2009. （in Chinese）

（编辑 王秀玲）

收稿日期：2021-08-29

基金项目：重庆市基础与前沿研究计划（cstc2015jcyjA00003）;国家自然科学基金（51308576）;重庆市自然科学基金（cstc2020jcyj-jq0087）

作者简介：刘东升（1962- ），男，教授，博士生导师，主要从事岩土工程可靠性分析、地质灾害风险评估理论研究及工程实践，E-mail：dshliu@vip.sina.com。

仉文岗（通信作者），男，教授，博士生导师，E-mail：zhangwg@cqu.edu.cn。

Received：2021-08-29

Foundation items：Chongqing Basic and Frontier Research Projects （No. cstc2015jcyjA00003）; National Natural Science Foundation of China （No. 51308576）; Natural Science Foundation of Chongqing （No. cstc2020jcyj-jq0087）

Author brief：LIU Dongsheng （1962- ）， professor， doctorial supervisor， main research interests： geotechnical engineering reliability analysis and geological disaster risk assessment， E-mail： dshliu@vip.sina.com.

ZHANG Wengang （corresponding author）， professor， doctorial supervisor， E-mail： zhangwg@cqu.edu.cn.AF9DA212-F27C-48ED-B9D1-A092D886E1D4