基于流固耦合的抽水蓄能机组推力瓦变形以及安全性能分析

2022-05-13洪云来章志平张送校吴中华王雪梅

水电与抽水蓄能 2022年2期

洪云来，秦程，杨雄，章志平，张送校，吴中华，王雪梅，张智，郑源

（1.江西洪屏抽水蓄能有限公司，江西省宜春市 336000；2.河海大学能源与电气学院，江苏省南京市 211100；3.河海大学水利水电学院，江苏省南京市 210098）

0 引言

近些年来，我国抽水蓄能电站建设取得了长足的进展。抽水蓄能机组启动迅速、调节灵活、负荷变化范围广，在削峰填谷、调频调压方面有着重要作用[1]。由于抽水蓄能机组具有转速高、工况复杂、工况切换频繁等工作特点，轴承振动、轴承磨损等一系列关乎机组安全运行的问题变得尤为严峻[2，3]。因此，对推力轴承的结构、强度进行计算和分析十分必要。

目前，国内主要采用流固耦合方法计算推力轴承强度[4]，屈波等[3]运用双向流固耦合技术对抽水蓄能机组推力轴承进行数值模拟，研究了机组稳态运行时推力轴承油膜的运行机制，分析总结了润滑参数与弹性模量对轴瓦压力分布的影响。于向军等[5]在基于间接耦合的方法基础上，通过流固耦合数值计算了大中型空轴式静压轴承，根据数据总结出轴承发生形变的规律以及影响形变的因素。孟凡明[6]通过运用非线性优化法与影响系数法，编制了轴承流固耦合有限元程序，使用三维热弹流分析计算了某水润滑轴承，比较实验结果，验证了所编写程序的有效与可靠性。

本文以江西洪屏抽水蓄能机组为对象，建立推力轴承流固耦合计算模型，先对油膜进行数值模拟，得到油膜的压力分布，然后将其加载到结构分析的推力瓦模型表面，计算推力瓦的等效应力和变形，最后进行推力瓦的刚度分析，研究了机组运行整个过程中油膜运行机制对推力轴承产生的影响。

1 数学模型的建立

1.1 推力轴承基本理论

推力轴承在水力机械中起到了至关重要的作用，是专门承受轴向力的机械部件[7]。整个轴的轴向力通过油膜传递到推力轴承的推力瓦上。在机组启动前，需通过高压油顶起装置让压力油到达推力瓦与镜板之间，并在其之间形成静压油膜，随着机组转速不断升高到达额定转速时，高压油泵停止工作，此时油膜依靠轴瓦与镜板之间的楔形间隙形成，称为动压油膜[8]。江西洪屏抽水蓄能机组每个推力瓦下方采用弹簧簇支撑，采用可撕调整垫保证各推力瓦在同一水平面上，每块推力瓦上均布置一个高压油进油口，机组开启时启动高压油顶起油泵[9]。

1.2 推力瓦三维模型

根据图1所示江西洪屏抽水蓄能机组的瓦面尺寸图，通过UG建立推力瓦的实体模型，其中，扇形瓦面两边各有一对称的斜坡，扇瓦内径890mm，扇瓦外径2010mm，额定转速500r/min，瓦块数为12[10]。图2为推力瓦的实体三维模型。

图1 瓦面结构与尺寸Figure 1 Tile surface structure and dimensions

图2 推力瓦三维模型Figure 2 Thrust tile 3D model

2 流固耦合分析

2.1 流固耦合基本理论

流体计算时，假设所计算流体为连续介质，均质各向同性并且为不可压缩流体，流体中的每个质点均处于热平衡状态。考虑到推力轴承中的流体同时存在层流流动和湍流流动，因此，采用κ-ω SST湍流模型。计算时流体满足时均连续性方程：

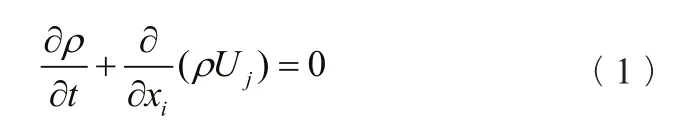
以及时均动量方程[11]：

对应的湍动能κ以及湍流频率ω方程分为式（3）和式（4）：

式中：下标f为流体，s为固体；τ为流体与固体应力；u为位移；q为热流量；T为温度。

2.2 流固耦合计算流程

由于油膜较薄，稳态运行时瓦面各点所受压力会引起相应各点产生一定的位移量，而各点位移又会反过来作用于瓦面的压力分布。可以借助ANSYS19.2中的Static Structural进行相应的单向流固耦合计算。

流体区域利用FLUENT对控制方程进行离散，采用SIMPLEC方法隐式求解速度和压力项，压力项采用二阶中心差分格式，对流项、湍动能及耗散率均采用二阶迎风格式[3]。进口位于两块轴瓦之间，因轴承流量一定，设置为速度进口条件，进油温度为35℃，进口速度为0.5m/s；出口位于模型外侧，设置为自由出流条件。镜板面设置为wall，转速为500r/min，设置油温为70℃。模型的两个侧面设置为周期性边界条件：φ1=φ2（其中：φ=u，v，w，k，∈），壁面为无滑移边界条件。固体区域利用稳态结构分析模块Static Structural，巴氏合金层下表面设置固定面约束[12]。

流体域采用动网格技术，并将油膜层下表面与巴氏合金层上表面设置为流固耦合面。计算时先求解润滑油流场，得到耦合面的流场压力，通过System Coupling将压力传递到结构分析模块，完成耦合面流场压力到固体变形的转化，反之亦然，从而保证耦合面数据实时传递。

流固耦合的数值模拟流程图如图3所示，首先在A中进行流体区域的数值计算，计算完毕后将流体耦合面处各点的压力传递到B中，然后在B中进行稳态结构计算，经过计算得出瓦面各点的位移变化。然后根据耦合面位移变化进行流体区域相应面网格的变形及体网格重构，接下来再进行下一轮的流体计算，之后重复前面的过程，经过若干轮计算与传递后停止计算，此时瓦面各处变形值及压力值满足设定的收敛条件。

图3 ANSYS流固耦合流程图Figure 3 Flow - solid coupling flow chart of ANSYS

2.3 结构场设置

计算区域分为流体区域与固体区域。由于流体计算区域比较复杂，故采用分块网格技术，各块之间采用交界面连接，其中，油膜部分均采用结构化网格。经网格数量无关性检验后确定油膜厚度方向分为6层，油膜网格数目为20万；非油膜区域采用非结构化网格，网格数目为25万；固体计算区域取巴氏合金层，采用类似油膜网格的划分方法，网格数为7万，见图4。采用非结构网格划分推力瓦结构。

图4 固体计算网格图Figure 4 Solid compute grid diagram

对结构体进行部分计算时，需要对推力瓦的各个方向添加约束条件。约束如图5所示：A为对推力瓦顶部的固定约束（fixed support），固定住推力瓦瓦面避免产生位移。B处为重力作用约束（standard earth gravity），推力瓦在工作时受到地心引力的作用，设置重力加速度为9.8066m/s2。

图5 推力瓦结构图Figure 5 Thrust tile structure drawing

在数值模拟计算时对推力瓦的工作进行了简化处理，认为每块推力瓦的瓦面油膜分布情况与运动规律相同，且油流过轴瓦与镜板之间对推力瓦的作用具有周期性，不同方位上推力瓦上的油膜分布情况与运动规律基本相同。本文选取一块推力瓦作为研究对象，探究不同转速工况以及不同油膜厚度情况下油膜对推力瓦产生的影响。

2.4 安全系数理论的定义

在机组运行时，推力轴承承受交变应力，因此，采用名义应力法进行分析。疲劳安全系数采用式（10）：

式中：nσ为疲劳极限；KσD为零件疲劳降低系数；σa为应力幅；[n]为许用安全系数。

3 计算结果及分析

3.1 不同转速下的计算结果与分析

选取4种不同的机组转速值，分别为100、350、500、725r/min（飞逸转速），此时取得油膜厚度为0.066mm。分别对这几个转速工况进行计算，结果如下。

3.1.1 不同转速下推力瓦应变对比

通过流固耦合计算可以得到推力瓦在不同转速的总变形分布情况。图6为机组在4个不同转速下推力瓦固体部分总变形图，可以看出当转速为100r/min时［见图6（a）］，推力瓦最大形变为3.25×10-3mm，随着转速不断增加［见图6（b）～图6（d）］，推力瓦的形变不断增加至2.22×10-2mm［见图6（d）］，总体呈现形变增大的趋势。对于推力瓦表面形变分布，对比4种工况最大形变位置几乎没有变化并且位于推力瓦中心处，从瓦面中心沿周向逐渐减小。可见，推力瓦的形变随转速升高而增加，同时最大形变位于推力瓦中心处。

图6 瓦面应变分布（单位：m）Figure 6 Thrust tile surface strain distribution（unit：m）

3.1.2 不同转速下推力瓦安全系数对比

图7为不同转速下推力瓦的安全系数，对比这4种转速工况下，转速为100r/min时［见图7（a）］，此时的推力瓦安全系数较高，但是再随着转速升高，推力瓦瓦面开始出现安全系数下降的情况［见图7（b）～图7（d）］。随着转速升高，瓦面低安全系数区域开始从瓦面中心向周围不断扩大，并且逐渐向推力瓦上侧靠近［见图7（d）］。随着转速升高，瓦面中心安全系数降低。结合图6可以看出，安全系数和瓦面应变分布相对应。由于转速升高推力瓦产生的形变逐渐变大，因此，瓦面中心的安全系数不断降低。为提高推力瓦的安全系数，应考虑选择合适的金属材料，减小推力瓦的形变，同时也应避免机组出现飞逸工况，以免出现推力瓦发生形变较大，安全系数降低的情况。

图7 瓦面安全系数分布Figure 7 Thrust tile surface safety coefficient distribution

3.2 不同油膜厚度下的计算结果与分析

在转速为500 r/min的情况下取4个工况点，即分别取油膜厚度为0.066、0.056、0.076、0.086mm，并对推力瓦在每个运行工况点下进行有限元求解，得到各个工况下推力瓦的应变及安全系数分布云图。

3.2.1 不同油膜厚度下推力瓦应变对比

从图8中可看出，当油膜厚度为0.056mm和0.066mm时，可以看出此时推力瓦受力不均匀［见图8（a）、图8（b）］；在这两种工况下，形变主要集中在瓦面中心处。当厚度为0.076mm时［见图8（c）］，发生最大形变的区域有所增大且向瓦面上侧靠近，其余区域沿最大形变中心向两边逐渐减小。当油膜厚度增加到0.086mm时［见图8（d）］，推力瓦应变分布与图6（a）、图6（b）相似，瓦面中心发生最大形变，由中心向周围发生的应变呈梯度减小。从总体趋势上看，随着油膜厚度的增加，最大形变的值呈现先增加后急剧减少的趋势。为减少推力瓦的形变对机组运行的影响，则需要维持合适的油膜厚度，尽量避免推力瓦出现较大形变。

图8 瓦面应变分布（单位：m）（一）Figure 8 Strain distribution on tile surface（unit：m）（No.1）

图8 瓦面应变分布（单位：m）（二）Figure 8 Strain distribution on tile surface（unit：m）（No.2）

3.2.2 不同油膜厚度下推力瓦安全系数对比

图9为不同油膜厚度下推力瓦安全系数，可以看出4个不同工况下，推力瓦的最小安全系数出现在瓦面中心处。从图中可看出，随着厚度增加到0.076mm，瓦面中心的安全系数不断减小［见图9（a）～图9（c）］，安全系数低的区域不断变大。当油膜厚度为0.086 mm时［见图9（d）］，瓦面中心的安全系数有所增加。总体上看，瓦面中心的安全系数随着厚度增加先减小后又有明显的增加。对比图8和图9，在油膜厚度为0.076mm时，发生最大形变的区域最大且安全系数较低的区域也最大，在机组运行时，应避免出现油膜厚度为0.076mm的情况或者避免长时间在该工况下运行。