融合一致性正则与流形正则的半监督深度学习算法

王杰，张松岩，梁吉业

1. 山西大学计算机与信息技术学院，山西 太原 030006；

2. 计算智能与中文信息处理教育部重点实验室，山西 太原 030006

0 引言

随着互联网和信息产业的飞速发展，人们采集与获取数据的能力大大提高，信息量以前所未有的速度增长。世界已进入大数据时代[1]，这些大数据蕴含着巨大的价值，对于社会、经济、科学等各个方面都具有重要的战略意义[2-5]，为人们更深入地感知、认识和控制物理世界提供了前所未有的丰富信息。大数据时代的到来引发了深度学习的研究热潮并取得了巨大的成功，但训练一个深度网络模型往往需要大量具有高质量标记的训练样本[6-7]。对于许多深度学习任务来说，获取大量用于训练的有标记样本的成本是极其昂贵的，且需要耗费大量的时间，与此同时，无标记样本的获取相对容易且廉价。因此，如何利用大量无标记样本来辅助提高学习方法的泛化性能，已成为一个重要研究问题。

为了应对这一问题，半监督学习（semi-supervised learning，SSL）应运而生，其目的是通过在模型训练中引入无标记样本来解决传统监督学习在训练样本不足时性能差的问题[8]。近年来，随着深度学习的兴起，半监督深度学习取得了很多显著的成果并受到越来越多的关注，其中基于一致性正则的方法[9-14]是半监督深度学习[15]研究中的热点问题之一。一致性是指模型对扰动后训练样本的预测结果应与原预测结果保持一致。由于这类方法并不依赖于样本的真实标记，因此可以使用大量的无标记数据。一致性正则鼓励预测函数对样本的邻域具有光滑性，使得样本点局部的预测是平滑的，这种具有局部平滑性的模型更容易推广。然而，基于一致性正则的方法仅仅考虑模型对样本的邻域具有光滑性，没有考虑数据流形结构，可能会使得一部分相近的样本得到差异很大的输出，导致分类器性能下降。如图1（a）所示，尽管内外圈的样本点均局部平滑，但外围点中出现了两处低密度空白区域，这样分类面可能会位于该低密度区域，使得外圈中右侧的样本错分，造成分类性能下降。图1中红色和黑色的实心点为两类有标记样本，空心点为无标记样本，紫色的虚线圈为样本点邻域的一致性表示，蓝色、绿色和黄色的实线为可能的分类面。

图1 基于一致性正则、流形正则的半监督学习方法以及本文提出方法的示意图

为了应对上述问题，本文提出一种融合一致性正则与流形正则的半监督深度算法SmoothMatch。流形正则[16-20]是基于半监督学习中常见的流形假设，即假设数据分布在流形上，邻近的样本拥有相似的输出值。这里的邻近程度常用相似程度来刻画。流形是在局部与欧氏空间同胚的空间，换言之，它在局部具有欧氏空间的性质，能用欧氏距离进行距离计算。针对每个样本点，基于欧氏距离找出其邻近样本点，然后建立一个邻近连接图，图中邻近点之间存在连接，而非邻近点之间不存在连接。这类方法将有标记样本和无标记样本映射为图，以近似刻画数据的流形分布，从而可以充分利用数据中蕴含的流形结构信息。但这类方法只能保证在构造的图上保持局部相似性，即相连的样本有相似的输出。当样本扰动方向不是沿着图所近似的流形时，预测函数对扰动的样本的预测可能会发生很大的改变，即模型不能为未见到的样本点提供合理的输出。如图1（b）所示，黄色、蓝色分类面分别靠近外圈和内圈的数据点，这会导致学习器的泛化性能降低。本文提出的算法综合了两类方法的优点，如图1（c）所示，本文提出的算法不仅考虑了每个样本点的局部预测平滑，也考虑了真实的邻近（相连）样本具有平滑性，使得模型充分利用了数据的结构（流形）信息，进而可以将分类边界推向合理的低密度区域，有效地提高半监督深度学习算法的性能。在多个图像和文本标准数据集上进行实验，与相关算法/模型相比，本文所提算法SmoothMatch的性能有明显提高。

1 相关工作

1.1 半监督学习

半监督学习是近20年发展起来的一类新型机器学习方法，目前半监督分类算法可以大致分为如下几类：基于支持向量机（support vector machine，SVM）的半监督算法[21]、基于协同训练的算法[22-23]、基于生成式的算法[24-25]、基于图的半监督算法[16-20]，以及半监督深度学习算法[15]。基于一致性正则的半监督学习算法[9-14]是半监督深度学习算法中一类非常重要的学习范式。除此之外，半监督学习算法还包括半监督聚类[26]和半监督回归[27]等算法。下面着重回顾与本文相关的基于图的半监督学习算法和基于一致性正则的半监督学习算法。

1.2 基于图的半监督学习算法

基于图的半监督学习利用有标记和无标记样本之间的联系得到一个关于样本空间的图结构，然后利用这个图结构将标记从有标记样本“传播”到无标记样本。如Zhu X J等人[16]提出了一种基于高斯随机场模型的半监督学习算法，该算法将有标记和无标记的数据表示为一个加权图，边上的权重表示数据之间的相似性。然后，学习问题被表述为图上的高斯随机场；Belkin M等人[17]引入图拉普拉斯正则化，将直推式图半监督学习拓展到归纳式，可以对训练集中没有出现过的样本进行分类，使得模型具备一定的通用性和泛化能力；Bai L等人[18]提出了一种新的标记传播算法，该算法将标记的成对关系作为约束条件，建立有约束的标记传播。Wang J等人[19]提出了一种基于图神经网络的半监督分类算法，该算法融合多个图神经网络的结果，在保证有标记节点分类正确的同时，利用大量无标记节点的伪标记信息最大化多个图神经网络的多样性，从而提升图半监督学习的性能。Liang J Y等人[20]提出了一种自适应构图的方法，将构图和标记推理集成到统一的优化框架中，实现二者的相互指导和动态提升，从而实现鲁棒的图半监督学习。

1.3 基于一致性正则的半监督学习算法

基于一致性正则的方法分为基于样本扰动的方法与基于模型扰动的方法。虽然二者在具体实现上有诸多不同，但目的都是最小化模型预测的一致性损失。

基于样本扰动的方法将原样本和扰动后的样本输入同一个模型中，然后最小化二者预测的不一致性。该类方法依赖于数据增广技术。为了产生高质量的扰动样本，近年来研究者提出了大量数据增广技术，如Miyato T等人[12]提出了虚拟对抗训练（virtual adversarial training，VAT）模型，其主要思想是找到使模型输出偏差最大的方向，然后在这个方向上对输入产生扰动；Verma V等人[13]提出了插值一致性训练（interpolation consistency training，ICT）模型，该模型将一个样本点沿另一个样本点的方向做扰动，模型对两个样本点间插值的预测结果应与模型对两个样本点预测结果的插值一致；谷歌的Berthelot D等人[9]融合多种数据增广技术提出了MixMatch算法，达到非常低的分类错误率。

基于模型扰动的方法将训练样本输入结构相同但参数不同的两个或多个网络中，实现模型预测的一致性。其中，Laine S等人[10]提出了Π模型和temporal ensembling模型。Π模型将训练样本输入两个结构相同的网络，两个网络使用随机Dropout技术产生不同的网络参数，最后最小化两个网络的预测结果，从而达到一致性正则化的目的；temporal ensembling模型首先计算训练样本在前几个训练轮次（epoch）中预测的平均值，然后最小化该平均值与当前epoch的预测值，利用多个epoch的预测来实现一致性。Tarvainen A等人[11]提出了mean teacher模型，与temporal ensembling对前几轮的预测进行平均不同，mean teacher对前几轮的模型参数进行平均，并最小化该模型与当前模型的预测值，从而实现模型扰动的一致性。

然而上述基于一致性正则的方法仅仅计算样本邻域内的一致性，并没有考虑数据点之间的连接，这样可能会缺失样本数据结构中的信息。因此，笔者将基于一致性正则的方法与基于流形正则的方法结合，提出一种融合一致性正则与流形正则的半监督深度学习算法SmoothMatch。

2 融合一致性正则与流形正则的半监督深度学习算法

在详细介绍算法之前，首先介绍算法中用到的部分变量：假设数据集D里有N个样本，其中为有标记样本集合，标记，共K个类别；为无标记样本集合。

本文提出一种融合一致性正则与流形正则的半监督深度学习算法SmoothMatch，其不仅对样本局部区域的扰动施加平滑约束，同时考虑了样本点之间的结构信息。算法的总体损失函数如下：

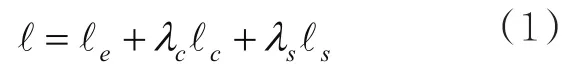
总体损失主要由3项构成：①对于有标记样本，比较模型的预测结果与样本的真实标记，计算交叉熵损失ℓs；②对于无标记样本，采用数据增广技术Augment(xu)计算一致性损失ℓs；③从有标记样本和无标记样本中抽取样本，将这些样本进行特征空间映射并构图，最后计算平滑性损失ℓs。λc与λs为防止某一项损失过大或过小而平衡3项损失的权值参数。算法整体框架如图2所示。

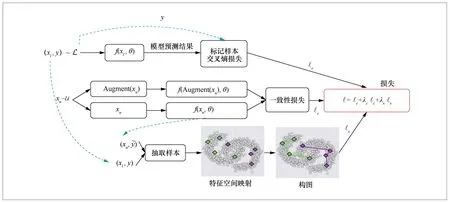
图2 算法整体框架

2.1 样本邻域内的一致性损失

本节使用ICT模型[13]中的数据增广方法Mixup来计算一致性损失。Mixup的基本计算式如下：

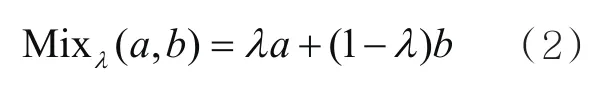
其中，λ为服从β分布的权值参数，Mixλ(a,b)为a和b之间的插值。

给定一个小批量（mini-batch）数据集中的任意两个样本点xi与xj以及模型预测结果f(xi,θ)和f(xj,θ) ，根据式（2）可以得到这两个样本点间的插值，则模型对该插值的预测结果为同时可以得到模型对样本点xi与xj预测结果的插值一致性 损 失 便是要求保持一致。因此，在一个mini-batch数据集内的一致性损失为：

2.2 样本间的平滑性损失

在大数据环境下，刻画样本间平滑性损失的流形正则项面临如下挑战。①大多数现有的构图方法是对输入空间的距离度量，但该类方法有很大的局限性。例如对于图像样本，其输入是多通道像素值，然而像素距离并不能很好地反映样本间的语义相似性。②传统基于图的算法计算整个数据集的邻接矩阵并在此基础上构图，耗费的时间过长、空间复杂度过高。③传统方法构建的是静态固定的图，因此不能利用分类器提取的知识进行图的动态调整。

为了解决这些问题，本文提出在minibatch数据集内构图并计算平滑性损失的方法。在样本的标记空间计算样本相似度，并采用动态构图的方式，随着学习不断更新图结构，从而更好地指导学习器学习样本间的平滑。

（1）构图与邻接矩阵的计算

在每一个mini-batch数据集内，用其中的数据构造K近邻（K-nearest neighbor，KNN）图，与传统构图不同的是，这里使用样本的标记空间度量样本间的相似度，权值矩阵计算如下：

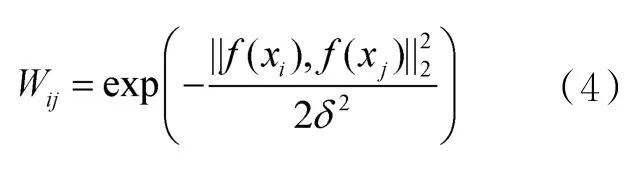
其中，δ>0是指定的高斯函数带宽参数，f(xi)是模型对样本的预测。

（2）平滑性损失计算

给定邻接矩阵W与样本特征表达后，平滑性损失如下：

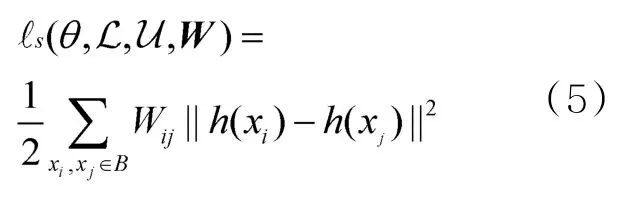
其中，h:X →Rp为输入空间到网络倒数第二层的映射。

2.3 算法实现细节

SmoothMatch的整体损失函数如下：

其中，wc(t)和ws(t)是随epoch迭代线性上升的权值函数。算法流程如下。

输入：有标记样本集合L，无标记样本集合u，随epoch迭代线性上升的权值函数wc(t)和ws(t)，模型f(xi;θ)，损失平衡项λc与λs，模型迭代次数numepochs

输出：更新后的模型参数θ

3 实验设计与分析

为了测试SmoothMatch算法的有效性，在3个图像数据集以及两个英文文本数据集进行实验，图像数据集分别为CIFAR-10、CIFAR-100和SVHN，文本数据集分别为IMDB和Yahoo！Answers。数据集介绍见表1。

表1 数据集介绍

本文数据遵循参考文献[28]的划分方法，对于图像数据集，CIFAR-10与CIFAR-100分别包括45 000个训练样本、5 000个验证样本和10 000个测试样本，SVHN数据集包括65 932个训练样本、7 325个验证样本和26 032个测试样本；对于文本数据集，IMDB数据集包括63 000个训练样本、7 000个验证样本和25 000个测试样本，Yahoo！Answers数据集包括45 000个训练样本、5 000个验证样本和60 000个测试样本。为了测试算法在半监督学习环境下的性能，标准做法是将大部分训练样本视为无标记数据，只随机抽取并使用小部分有标记数据。

3.1 基线方法

对于图像数据集，对比Π模型[10]、mean teacher模型[11]、VAT模型[12]、MixMatch算法[9]以及本文的SmoothMatch算法的实验结果。为了确保对比实验一致，实验使用Wide ResNet-28模型，模型结构与详细说明参照参考文献[28]，学习率衰减值为0.999，权值衰减值为0.02。

对于文本数据集，对比Xie Q Z等人[14]提出的一致性算法UDA，以及预训练的BERT模型[29]。对于英文文本的数据增广，使用德语作为中间语言的回译过程，即将一个英文样本先翻译为德语，再翻译回英文样本。

关于超参数λc与λs，根据参考文献[28]的建议将CIFAR-10、CIFAR-100和SVHN的λc分别固定为75、150和250，并将IMDB和Yahoo！Answers的λc固定为100。各个数据集的λs从集合中遍历取值，并用验证集交叉验证取得最优值。模型的迭代次数由验证集损失确定，即当验证集的损失在一定迭代次数（本文为50次）内变化不大时，停止模型的迭代。

3.2 实验结果与分析

对于CIFAR-10和SVHN数据集，在250、500和1 000这3个不同数量标记样本上评估5种算法/模型的错误率，结果见表2和表3。对于CIFAR-100数据集，使用10 000个有标记样本对5种算法模型进行实验，结果见表4。

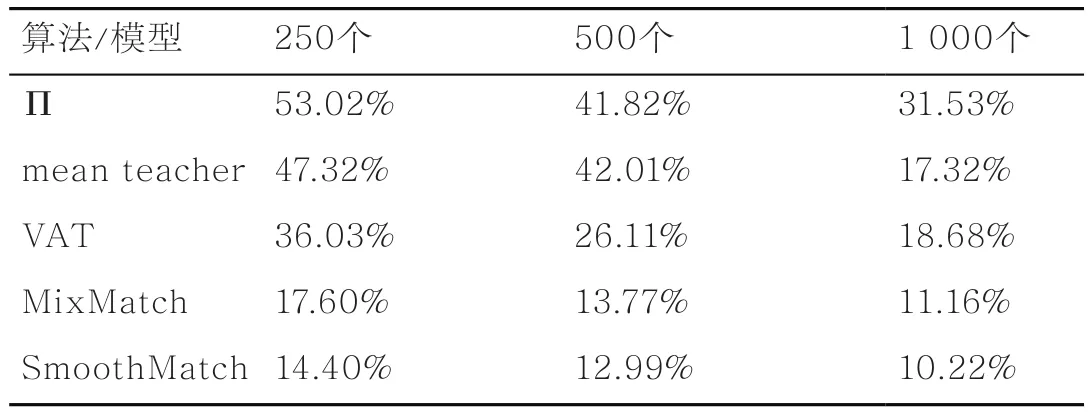
表2 5种算法/模型在CIFAR-10数据集上不同标记样本数下的错误率

表3 5种算法/模型在SVHN数据集上不同标记样本数下的错误率

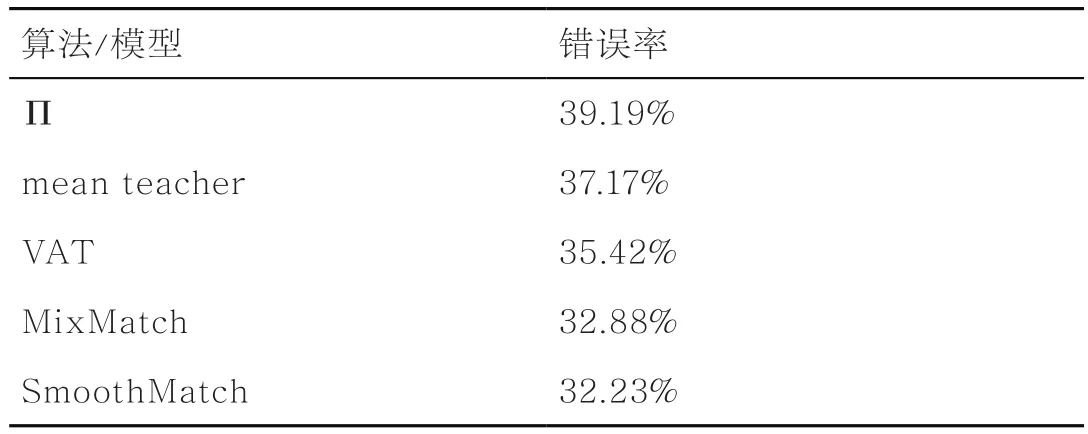
表4 5种算法/模型在CIFAR-100数据集10 000个标记样本下的错误率

由表2~表4可以得到如下结论。①SmoothMatch算法在3个图像数据集的各种标记样本数量下的准确性优于其他方法，例如，在CIFAR-10数据集上，在仅有250个有标记样本下SmoothMatch算法的错误率为14.40%，而相同条件下的MixMatch算法错误率为17.60%；在SVHN数据集上，当有250个有标记样本时，SmoothMatch明显优于Π模型，这表明了融合一致性正则和流形正则的有效性。②随着有标记样本数量的增加，上述几种方法的错误率均降低，这是因为有标记样本越多，所提供的监督信息越多，分类器能更好地拟合数据。特别地，在CIFAR-10数据集上，mean teacher模型的错误率有明显的降低，这说明该方法对有标记数据的依赖性很强，而本文所提算法由于可以充分利用数据的流形结构，能够使相似（相连）的样本有相似的输出，从而降低了对有标记样本的依赖性，可以在有标记样本较少的情况下达到不错的效果。

此外，笔者还验证了SmoothMatch算法在文本分类任务上的表现。IMDB和Yahoo！Answer数据集上的实验结果见表5和表6。

由表5和表6可以得到，SmoothMatch算法在两个文本数据集上均优于UDA算法和BERT模型。特别地，在IMDB数据集上，SmoothMatch算法在有标记样本数为20时的错误率为12.27%，明显优于BERT在有标记样本数为100时的结果，这说明了所提算法的优越性。

表5 3种算法/模型在IMDB数据集上不同标记样本数下的错误率

表6 3种算法/模型在Yahoo！Answer数据集上不同标记样本数下的错误率

图像数据集和文本数据集上的实验结果表明，融合一致性正则和流形正则的方法在考虑样本局部预测平滑的同时，充分利用了数据的流形结构，使得相似的样本有相似的输出，提高了模型的泛化性能。

3.3 参数分析

为了进一步分析一致性正则和流形正则对模型的影响，在3个图像数据集上对比了SmoothMatch算法在不同λs/λc比值下的错误率。3个数据集上的实验结果如图3所示。

图3 3个图像数据集上SmoothMatch算法在不同 λ s /λc比值下的错误率

可以看出，当λs/λc为0，即只利用一致性损失优化目标函数时，其错误率均处于较高水平。但随着平滑性损失权值λs的提高，错误率逐渐降低，到λs/λc为0.1时到达最优。由此可见，平滑性损失的加入使得模型对同一类样本的低维表示更集中，相邻的样本得到相似的输出，从而提高了模型的鲁棒性。而若继续加大sλ，则弱化了模型的一致性正则，使得样本点局部邻域的预测不平滑，导致错误率逐渐提高，模型的性能降低。这说明了一致性正则与流形正则的合理结合确实能够提高算法的性能。

4 结束语

本文针对基于一致性正则的半监督深度学习算法可能会使得一部分相近的样本得到差异很大的输出，进而导致学习器性能退化的问题，提出了一种融合一致性正则与流形正则的半监督深度学习算法。该算法在对模型施加一致性约束的同时，对样本构图并加入平滑性损失，实现了每个样本点局部邻域的平滑以及样本点之间的平滑，从而提高半监督学习算法的泛化性能。在多个图像和文本数据集上的实验结果表明，融合一致性正则与流形正则的半监督深度学习算法获得了更优的性能。