基于Wang transform的医疗保险期权定价研究
——以天津市职工医疗保险为例
2022-05-13贾圣杰
贾圣杰
(南开大学金融学院,天津300350)
基本医疗保险是我国社会保险制度中最重要的险种之一,为建立多层次的医疗保障体系做出了突出贡献。随后大病保险的进一步实施减轻了参保职工或居民由于患大病而产生的高额医疗负担,这是我国基本医疗保险制度的拓展和延伸,也进一步完善了我国的医疗保障体系。但近年来我国学者对基本医疗保险或大病保险的探讨主要集中在制度层面,对定价方面的研究甚少。诚然,部分原因可能是相应保险基金的筹集坚持“以收定支、收支平衡”的原则,看似无需进行定价研究。然而,大病保险的开展是政府采用公开招标的方式选定保险公司承办的,实际结果表明,由于定价存在不足以及双方合作程度较浅等原因,承办的保险公司盈利空间较小,有的甚至出现了亏损[1]。因而对基本医疗保险以及大病保险进行定价研究是必要的,合适的定价方法可以同时适用于社保和商保,实现二者定价方法的相通,有助于打破双方合作的局限性、加深社保与商保的合作,对构建覆盖全民的社会保障体系意义深远。另外,在实施“健康中国”战略的背景下,新型商业补充医疗保险产品也会逐渐涌现,由于数据或经验不足等原因,一些传统的精算定价方法可能会面临较大挑战,如何对这些产品进行合理定价将成为一个核心问题。针对以上问题,本文将期权定价方法引入医疗保险纯保费的费率厘定范畴,对传统的精算定价方法进行补充和改进,具有较强的理论价值和现实意义。
一、文献综述
从理论上而言,期权与保险具有很强的相似性,这为把期权定价方法引入保险产品的定价中奠定了理论基础。一方面,保险可以视为一种期权:保险公司与投保人签订的保险合同类似于一份期权合约,是投保人为了规避未来时期其资产价值下降的风险而购买的一份欧式看跌期权。另一方面,期权也可以视为一种保险:期权买方相当于投保人,支付一定数量的保费以获得未来潜在收益(补偿);期权卖方则相当于保险人,收取保费并承担相应的风险[2]。
Merton(1977)[3]首次提出了期权定价模型在保险中的应用,该方向逐渐引起一些学者的重视。Doherty 和Garven(1986)[4]利用离散时间的期权定价模型研究了财产和责任保险公司的合理收益率;Cummins(1988)[5]认为保单与期权类似,都是一种或有索求权,并将基本的期权定价模型引入到保险保证基金的收费计算中。随后期权定价模型在财产保险、人寿保险的一些领域得到了一定发展,特别是在与自然灾害相关的再保险中得到了广泛应用,但在医疗保险方面的研究和应用则相对较少,主要原因在于:与一般金融资产不同,医疗保险产品定价时所面临的各种风险,比如健康风险等,无法在市场上进行连续交易,更无法进行卖空操作,这些风险所面临的市场是不完美、不完备的。针对这些问题,胡仕强(2014)[6]指出,传统的精算定价方法忽视了金融市场的作用,与现实不符;在无套利和完备的市场中,保险未定权益可以通过市场进行完美复制,BS期权定价因植根于市场均衡理论而优于传统精算定价方法;而在市场不完备、BS方法无法应用时,可以使用Esscher测度变换来得到风险中性的保险定价。郑红等(2010)[7]则在一般经济均衡框架下重新推导期权定价模型,尝试将保险精算与期权定价进行统一。在医疗保险期权定价的实证研究方面,宋湘宁(2010)[8]基于供需均衡原理对高额医疗费用保险的期权定价方法进行了研究;郑红和游春(2011)[9]则探讨了补充医疗保险的障碍期权定价方法。在此基础上,本文将基于Wang transform进行医疗保险的期权定价模型构建,并对宋湘宁与郑红等人的一些模型假设进行改进,使模型更加完善、更符合现实,随后利用天津市职工医疗保险的相关数据进行实证研究以验证本文模型的有效性。
二、Wang transform简介
为了找到可以对各种或有权益进行定价的通用方法,Wang(2000,2002)[10-11]定义了一种“失真测度”(distortion measure)——Wang transform,其作用是对资产或风险的原初分布进行一定的调整或转换,从而得到相应的新分布,即进行了一种测度变换。
考虑[0,T]时期内的一个金融资产或者保险风险,其在时刻t(0 ≤t≤T)的值记为X=Xt,并将随机变量X的累积分布函数记为F(x)=P(X≤x)。则Wang transform的具体形式如下:
其中,Φ(·)和Φ-1(·)分别为标准正态分布的累积分布函数及其反函数;参数λ表示“风险的市场价格”,反映了系统性风险的水平。
参数λ的确定方式如下:首先为λ选定一个初值λ0,λ0一般可以取为经验夏普比率(empirical Sharpe Ratio),即,其中rX和σX分别为X在过去T时期内收益率(或增长率)的样本均值和样本方差,r为相等时期内的无风险利率。这样由Wang transform可以得到X的新分布,并计算新分布下X在未来T时刻的期望值E(X*T)。根据无套利原则,用无风险利率将E(X*T)贴现到当前时刻,其贴现值应该与X的当前值相等。如果两者不相等,则需相应地调整λ的取值并重复上述过程,不断迭代,直至最终选出符合无套利原则的λ值。
上面的计算过程可能略显繁琐,但利用统计软件可以相对容易地实现该过程。如果X符合特定分布,那么根据Wang transform 具有的一些性质,可以使相关计算得到大幅简化:
(i)如果X服从正态分布N(μ,σ2),那么经过Wang transform 调整的F*(x) 服从正态分布N(μ-λσ,σ2);
(ii)如果X服从对数正态分布LN(μ,σ2),那么经过Wang transform 调整的F*(x) 服从对数正态分布LN(μ-λσ,σ2)。
在计算得到经过Wang transform调整的F*(x)后,就可以利用X的新分布为相应的金融衍生品或者保险产品进行定价。
三、模型构建
(一)利用Wang transform进行分布调整
考察定义在期间[t,T]的随机变量S,St表示期初的人均累计医疗费用,ST表示截至时刻T的人均累计医疗费用。假设医疗费用S的变化满足

其中μ、σ均为常数,B为标准布朗运动。
令f= lnS并对df使用伊藤引理,可得该式表明,lnS是一个带漂移项的布朗运动,其漂移率为,波动率为σ。由布朗运动的性质可知,对于任意的t和T,给定St,lnST服从正态分布N(lnSt+可见,当医疗费用符合上述几何布朗运动时,意味着其符合对数正态分布。
接下来对随机变量ST进行Wang transform 调整。由Wang transform 的性质(i)可知,给定St,此时ST将服从均值为ln、方差为的对数正态分布。计算可得此时ST的期望值为根据无套利原则,以无风险利率r(连续计息)贴现到时刻t的值应该与S的期初值St相等,即

解得

将计算出的λ值代入替换,可最终确定出经过Wang transform调整的ST的分布,即给定St,
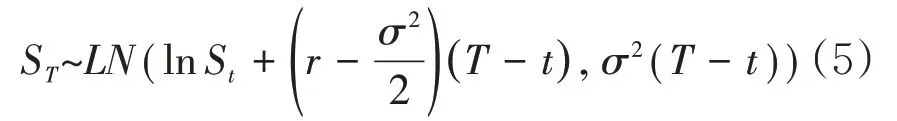
(二)初步形式
为方便推导,引入以下变量和符号:保险期间为[t,T],St与ST的含义同前,C()St,t,T为t时刻收取的纯保费,K为免赔额,α为赔付比例,L表示最高赔偿限额,r为连续计息的无风险利率,并假设在保险期间内至多包含一次索赔,且索赔总是发生在期末时刻T,索赔发生后保险责任随即终止。在保险有效期内,当被保险人的医疗费用累计额ST低于免赔额K时,由被保险人自负;当ST超过免赔额K时,免赔额之上的部分由保险人和被保险人共同负担,保险人负担的比例为α,且赔付额最多为L。则索赔发生时的赔付额G(ST)为:
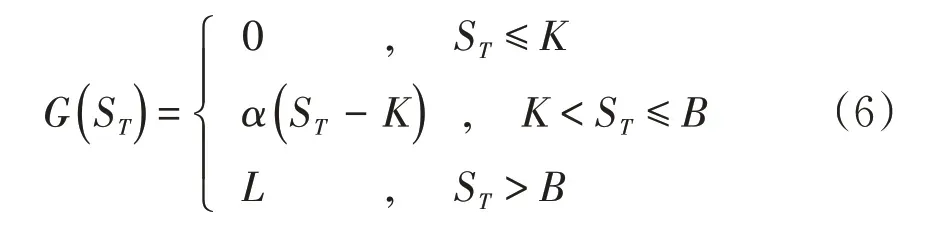
此时,保险人向投保人收取的纯保费应该等于保险人所承担费用期望值的贴现值。则在t时刻收取的纯保费应为
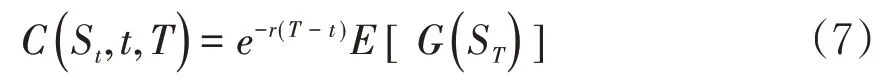
为简化计算,记
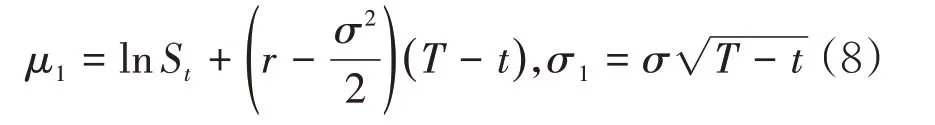
则ST的概率密度函数为
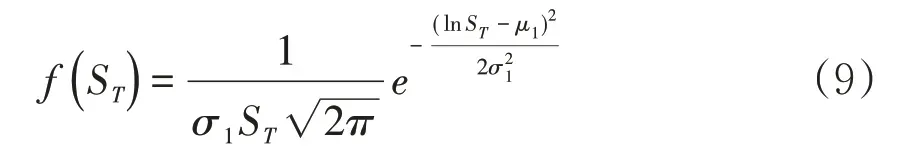
将式(9)带入式(7),进行y= lnST换元,计算整理并用式(8)替换掉μ1、σ1后可以得到:
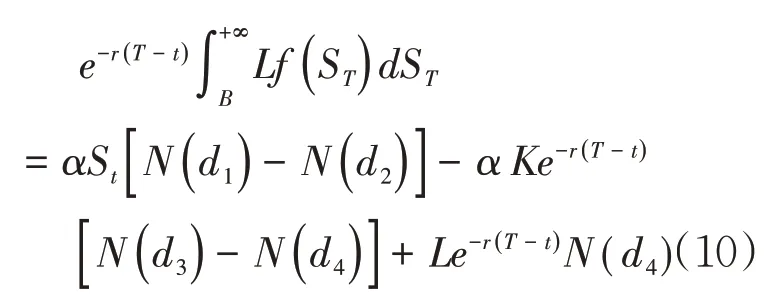
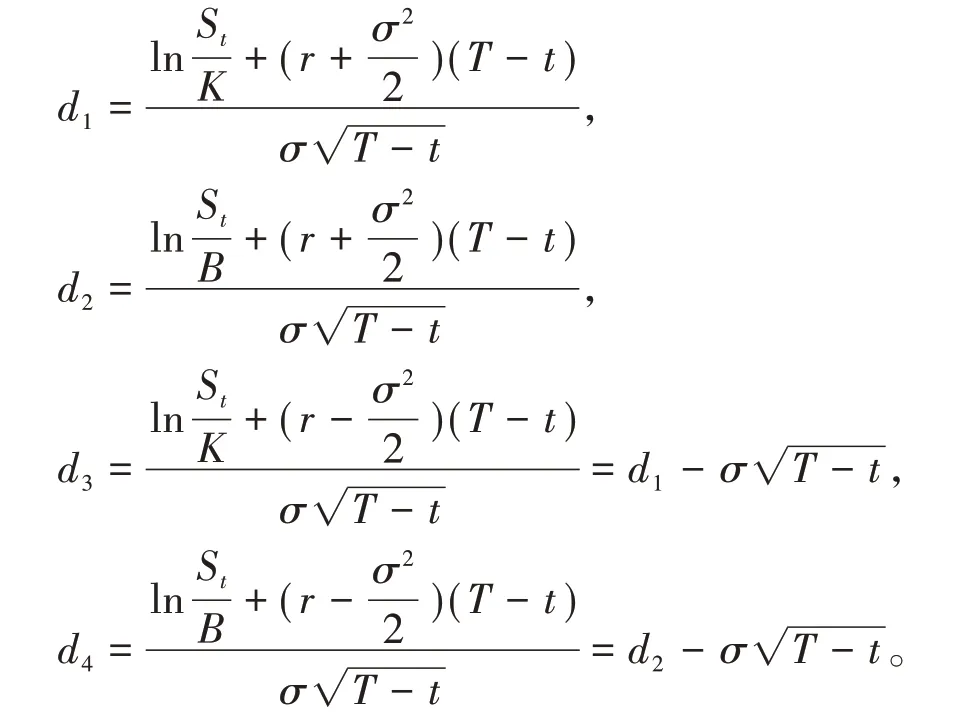
(三)最终形式
在进行上述推导时,本文曾假设在保险期间内至多包含一次索赔,且索赔全部发生在期末时刻T。但是对于一份保险而言,假定其发生索赔的时刻总是位于期末是不太合理的,除非保险期间特别短以至于索赔发生的概率可视为在保险期间内不变以及索赔金额的时间价值可以被忽略。
由于St的变化路径已知,可以作出如下改进:对于一份保险期间为[t,T]的医疗保险,仍假设在保险期间内至多发生一次索赔,且索赔后该保险合同立即终止,但对索赔可能发生的时刻不做限制,即索赔可能发生在保险期间内的任意时刻。
假设索赔发生的时刻为τ,τ∈[t,T],其概率密度函数表示为g(τ),并记改进后的医疗保险纯保费为,则可得
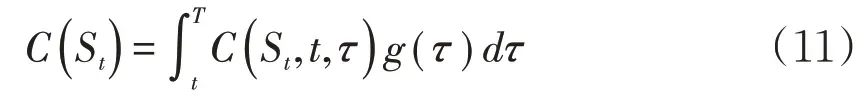
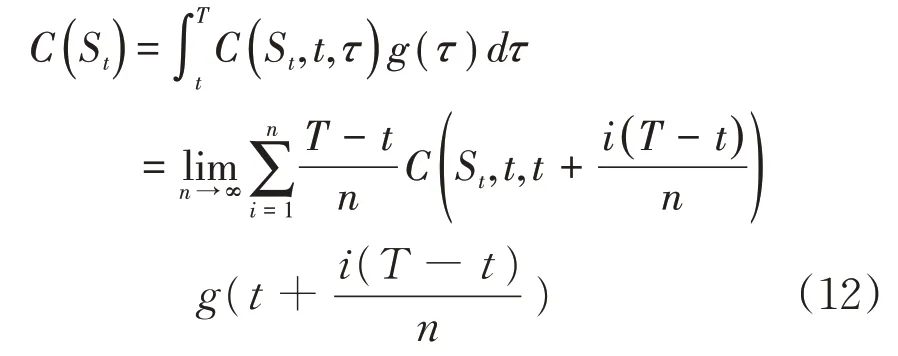
这时只要逐渐增加n的取值,就可以不断逼近的精确解,通过编程可以容易地实现该过程,进而得到所需要的数值解。
如果τ服从[t,T]上的均匀分布,即,则此时可以简化为
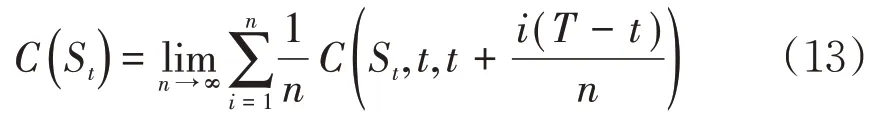
四、实证分析
本节将利用2002-2019年天津市“住院病人人均医疗费用”的年度数据①对模型进行实证检验,目标是利用该数据分别对2017-2020年天津市城镇职工基本医疗保险的住院保障部分进行定价测算,并将模型预测的纯保费与实际收取的保费进行比较来检验本文模型的有效性。
(一)样本数据的对数正态分布假设检验
由于本文模型假设住院病人人均医疗费用Si服从对数正态分布,所以首先对样本是否服从对数正态分布进行假设检验,检验通过后方可利用上述模型计算纯保费。
因为本文选取的是年度数据,所以保险期间定为一年,即T-t= 1。
由于无法直接检验一组数据是否服从对数正态分布,考虑把样本数据Si取自然对数得到lnSi,若Si服从对数正态分布的假设成立,则有(lnSi-lnSi-1)服从正态分布。记Di= lnSi- lnSi-1,那么只需要检验时间序列Di是否服从正态分布即可。由样本数据得出的时间序列数据Di如表1所示。
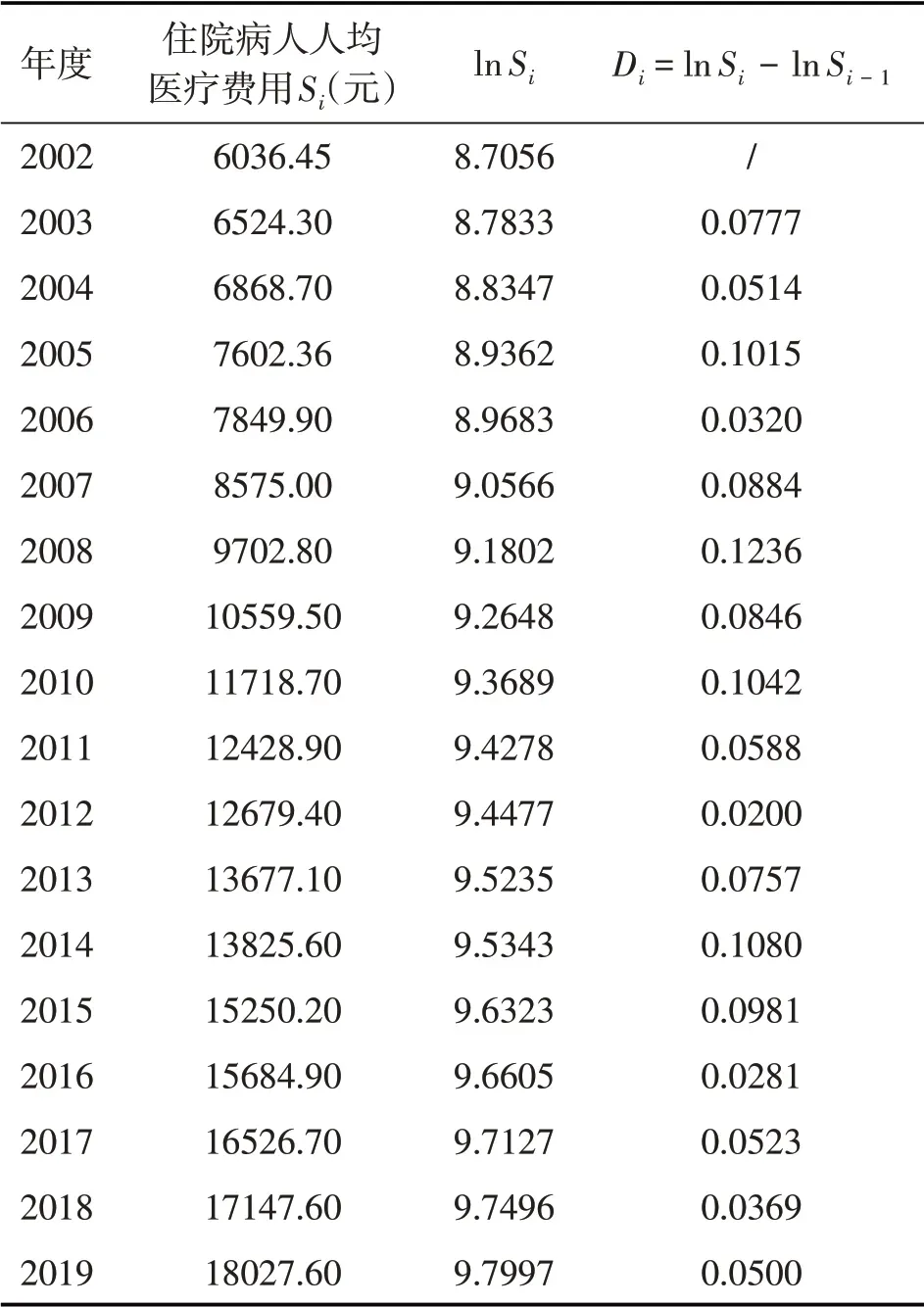
表1 2002-2019年天津市住院病人人均医疗费用的时间序列数据Di
本文选用Shapiro-Wilk 检验(W 检验)对Di进行正态性检验,该检验会返回一个统计量W和p值。当W 接近于1,且p 值大于0.05 时,不能拒绝原假设,即有理由相信样本数据的确服从正态分布。具体来说,利用R语言编程软件中的shapiro.test(x)函数(其中x为数值型向量)处理得到的结果如表2所示。
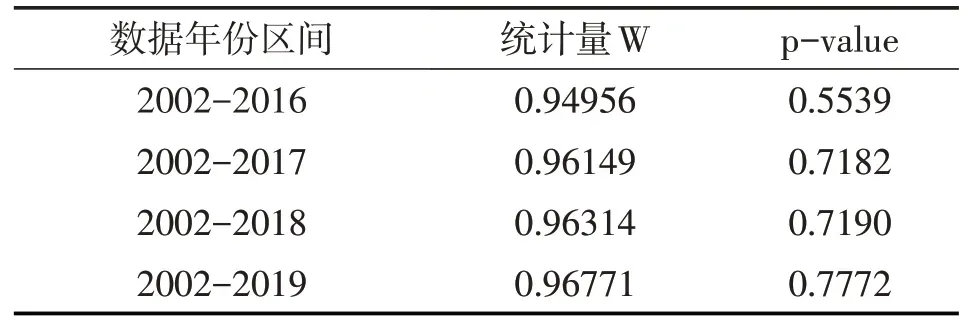
表2 不同年度区间内样本数据的Shapiro-Wilk检验结果
可以看出,以上各个年度区间内的样本数据均服从对数正态分布,表明模型的假设成立,接下来即可利用前文推导出的模型进行具体的定价测算。
(二)模型相关参数的选取与计算
1.波动率σ
由式(5)可知,当T-t= 1 时,时间序列Di服从以σ2为方差的正态分布。因而只需求出各个年度区间内Di的样本方差S2,由即可得到相应年度区间内σ的估计值̂,结果见表3。
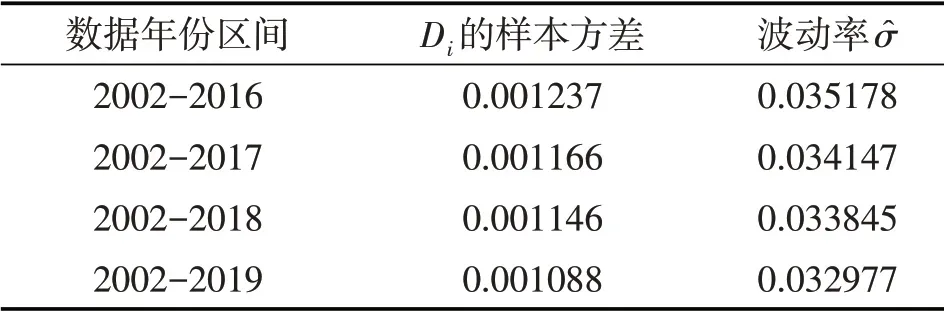
表3 不同年度区间内波动率σ的估计值
2.无风险利率r
无风险利率选为我国一年期定期存款基准利率。从2015年至今,该基准利率一直维持在1.50%的水平,将其转化为连续复利形式:r=1.489%。
3.赔付比例α、免赔额K和最高赔偿限额L
职工基本医疗保险基金由统筹基金和个人账户组成,个人账户主要用于小病或门诊费用,统筹基金主要用于大病或住院费用。基金支付的医疗费用设置有起付标准、最高支付限额和支付比例。起付标准一般为当地职工年平均工资的10%左右,最高支付限额为当地职工年平均工资的4倍左右。起付标准以下的医疗费用,从个人账户中支付或由个人自付;起付标准以上、最高支付限额以下的医疗费用,主要从统筹基金中支付,个人也要负担一定比例。
结合天津市的相关政策,以及本文假设一年内仅有一次索赔但实际索赔可能多于一次,所以适当上调免赔额K为当地职工年平均工资的20%,赔付比例取为α= 80%,最高赔偿限额L=α*当地职工年平均工资*(4 - 20%)。
从天津市人力资源和社会保障局的官网可以得到2016-2019年天津市职工平均工资数据,将各年度的人均工资数据作为下一年度的计算基数,可以确定出2017-2020年的免赔额等数据,具体如表4所示。
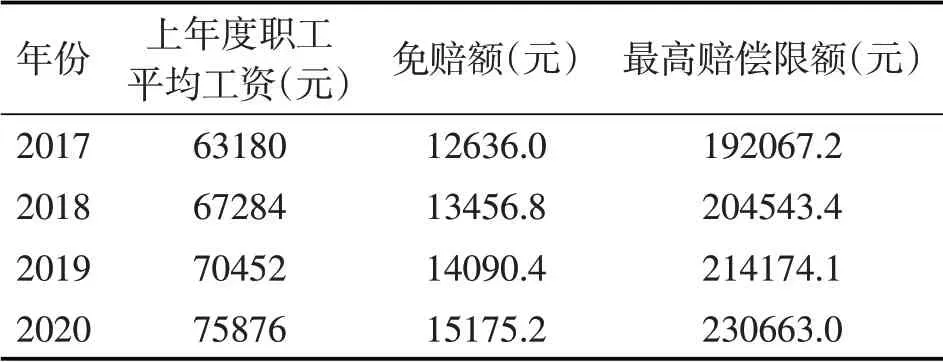
表4 2017-2020年天津市职工医疗保险的免赔额和最高赔偿限额
(三)模型测算
由于职工医疗保险的参保人群足够多,所以有理由认为保险索赔发生的时刻服从均匀分布。在得到模型相关的数据和参数后,将其带入式(13),再结合式(10),即可求得相应的纯保费。图1显示了当n分别取2、10、100 和1000 时由模型预测的2017-2020年的纯保费,可以看到,随着n的不断增加,相邻两线条之间的间距逐渐缩小,表明纯保费数值随着n的增加而逐渐收敛。
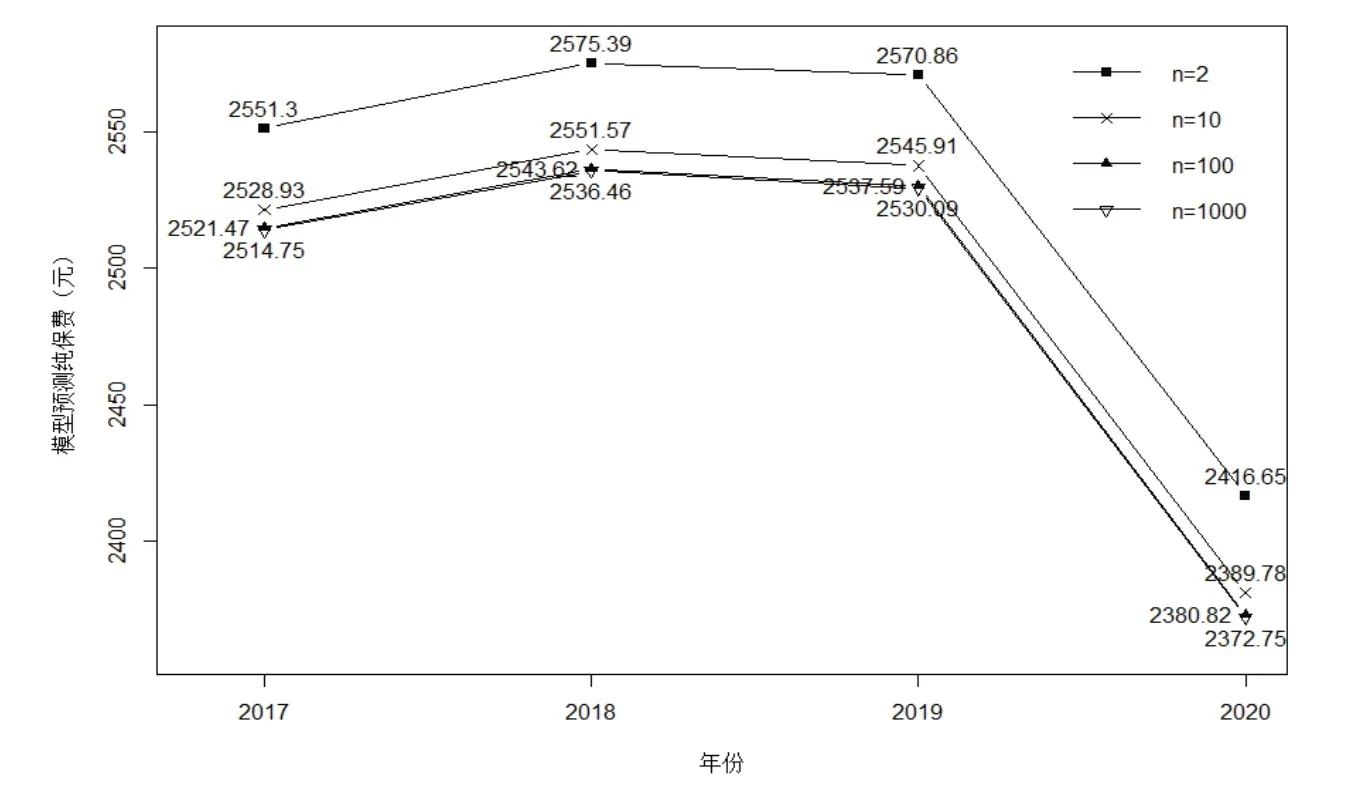
图1 n取不同值时2017-2020年模型预测纯保费
为进一步研究各年度纯保费数值的收敛性,继续增大n的取值,可以得到更为详细的收敛效果,具体如表5所示。当n达到百万级别(及以上)时各年度纯保费数据收敛到某一定值,不再随n的增加而变化,相应的收敛值即为纯保费的精确解。据此最终可得2017-2020年模型预测纯保费分别为2514.00元、2536.67元、2529.26元和2371.85元。
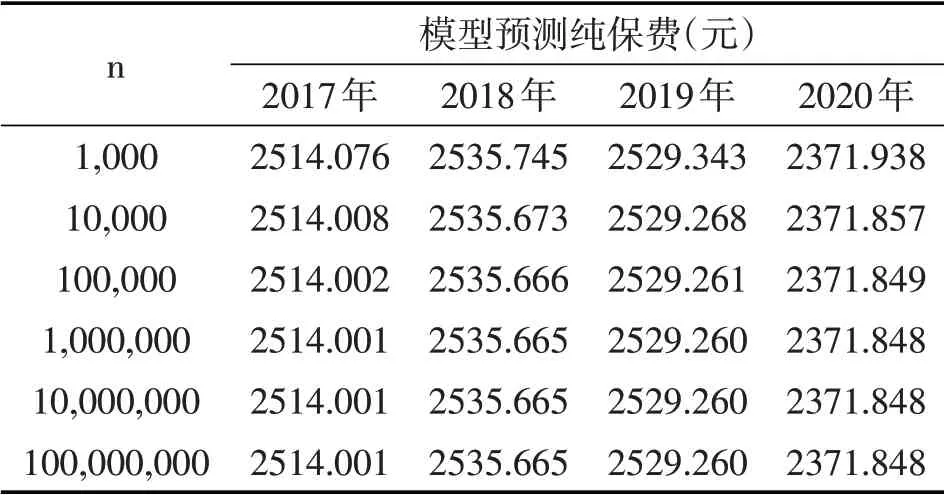
表5 n取不同值时2017-2020年模型预测纯保费数据的收敛情况
接下来将模型预测纯保费与实际收取的总保费进行比较。由于职工医疗保险的保费收入划分为个人账户和统筹基金两部分,且统筹基金主要用于支付住院医疗费用,而本文所研究的医疗保险就是为了补偿病人的住院医疗费用,所以该保险的保费就近似对应职工基本医疗保险的统筹基金部分。另外,职工医疗保险的保费由个人和单位共同缴纳,根据天津市相关规定,职工个人缴纳的基本医疗保险费(缴费基数的2%)全部计入个人账户;用人单位缴纳的基本医疗保险费(缴费基数的10%)分为两部分:一部分用于建立统筹基金(70%),一部分划入个人账户(30%)。故总保费收入划入统筹基金的比例约为7/12。这样只需要找到天津市职工医疗保险的参保人数和保险费总收入数据,就可以间接计算出人均收取的总保费(实际收取保费),具体如表6所示。

表6 2017-2020年实际收取的人均总保费②③
图2 展示了2017-2020年模型预测纯保费与实际收取总保费的对比情况。二者的走势基本保持一致,且后者一直大于前者,与实际相符合。更具体地计算各年度下的比值ratio=实际收取总保费/模型预测纯保费-1,可以得到2017-2020年ratio的值分别为17.87%、15.94%、22.86%和20.18%,这表明每年实际收取的附加保费约为纯保费的20%,在合理范围内,从而也验证了本文模型的有效性。
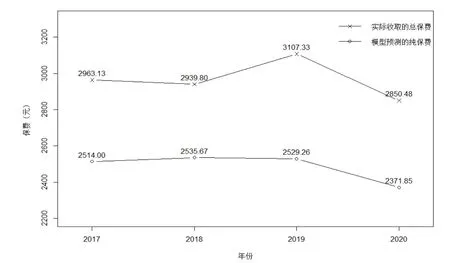
图2 2017-2020年模型预测纯保费与实际收取总保费的对比
五、总结
本文基于Wang transform 将期权定价方法引入医疗保险的精算定价中,构建出相应的模型,并利用天津市职工医疗保险的相关数据进行了实证研究,计算出模型预测的应收取纯保费,随后将该测算结果与实际收取的总保费进行了对比,最终的结果验证了本文模型的可靠性和有效性。本文模型是对基本医疗保险定价研究的有益尝试,也是对传统精算定价方法的补充和改进,不仅丰富了医疗保险定价方法的研究,也具有一定的现实参考价值。
[注释]
①数据来源:《中国卫生健康统计年鉴》。
②数据来源:《中国卫生健康统计年鉴》,天津市财政局。
③自2019年起,生育保险基金并入职工基本医疗保险基金,统一征缴,统筹层次一致。本表所展示的保费收入或基金收入数据均已经扣除了生育保险对应的部分。
