基于BP 神经网络的高速公路旅行时间预测模型

樊 博，马 切，雷小诗，马筱栎

（1.重庆交通大学交通运输学院,重庆 400074；2.西华大学理学院，四川 成都 610039；3.成都工业学院，四川 成都 611730）

对交通系统而言，旅行时间是评价道路运行状态的重要指标；对交通管理者而言，旅行时间是诱导公众出行、辅助管理人员合理配置管控资源的重要依据；对公众出行而言，旅行时间是制定出行规划的重要参考。因此，科学有效地预测旅行时间是先进的交通管理系统和出行者信息系统中不可或缺的部分，其对于提高交通运行效率有重要意义。

我国研究人员在开展高速公路旅行时间预测相关研究时，大多受限于视频监控设备覆盖率较低、路网浮动车较少、道路检测器铺设密度较低等原因，导致用于研究的数据来源渠道虽广，但其所覆盖的空间范围较小（多为事故多发点、拥堵瓶颈点或其他特殊路段等）。与此同时，我国高速公路在日常运营中会产生海量的联网收费数据，相比其他必须使用专用设备才能获取的数据源而言，其获取成本和方法更占优势，而且在正常情况下收费数据能覆盖进出高速公路的每一辆车，数据中还包含有车辆载重、车型车种等其他数据源难以获取的信息。

已有文献中，利用收费数据开展的研究有出行群体聚类[1]、交通状态判别[2]以及道路通行费预测[3]等。然而总体上，收费数据利用程度较低，其使用价值未被完全利用。就预测旅行时间而言，以往研究多数是基于浮动车数据[4]、车辆检测器数据[5−6]以及视频监控数据[7]等开展的研究工作，而收费数据中记录了路网上所有车辆进出高速公路的详细时间，这为预测旅行时间提供了基本条件。例如，王翔等[8]构建了基于改进最近邻非参数回归的方法旅行时间预测模型，陈娇娜等[9]提出了基于Bootstrap-KNN 区间的旅行时间预测模型，且均通过实例验证了模型的有效性。

本文利用重庆高速公路联网收费数据，开展站间旅行时间预测研究。首先利用随机森林算法从影响旅行时间的备选变量中筛选出重要变量，再使用BP 神经网络建立旅行时间预测模型，模型中同时考虑了路段长度、不同时段等因素，最后基于重庆高速公路路网收费数据对模型进行实例验证。

1 数据准备

1.1 数据来源

本文基于重庆高速公路路网2017 年至2018 年联网收费数据开展研究，以G65 包茂高速渝湘段某全长为84.5 km 的道路作为研究通道（下文简称“通道”），提取与该通道相关的10 余个收费站的收费数据。将原始收费数据导入到数据库后，一条完整的收费数据所包含的必要字段有车辆车牌号、车辆驶入和驶出某收费站的时间和收费站的编号、客货车标识、行驶距离等。在使用收费数据前须将错误数据删除（例如字段缺失、字段取值或属性无效、车辆进出收费站的时间不合逻辑等）。

1.2 旅行时间提取

如图1 所示，A、B 收费站间形成一个基本路段，称之为路段或站间。

图1 高速公路收费站间示意图

站间旅行时间指某周期内由A 入口驶入、B 出口驶出高速公路的所有车辆的平均行驶时间，因此可根据收费数据中车辆经收费站进出高速公路的时间来计算，以站间k 在周期T内的旅行时间为例：

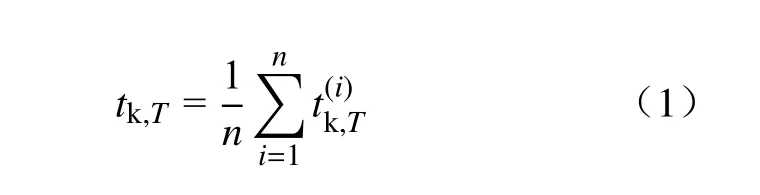
式中：tk,T为 k 站间在周期T内的旅行时间，单位为min；n为 周期T内所有由A 入口驶入、B 出口驶出的车辆总数；为第i辆 车（i=1,2,···,n）的旅行时间，其通过车辆驶入、驶出收费站的时间计算而得，即字段EXTIME 与ENTIME 的差值。

既有研究中，一般取10～15 min 时间间隔为一个研究周期[6−9]。考虑到本文使用的联网收费数据中仅记录了车辆驶入和驶出相关收费站的信息，以10 min 为一个研究周期可能会导致周期内样本数量较少，因此本文取15 min 作为一个周期。再者，统计发现，一型客车全年占据通道内交通流量的绝大部分，客货车流量比值也基本维持在相对稳定的水平，并且相关研究表明，高速公路交通系统中，可用一型客车的旅行时间来推算其他车型的旅行时间，因此本文主要以一型客车的旅行时间作为研究对象。同时，数据显示，路网在夜晚和凌晨时段流量相对稀少，该时段下车辆以自由流速度行驶，无预测必要，因此本文研究时段为7:00—20:00。

1.3 旅行时间的修正

由于某些特殊驾驶行为（例如在正常交通状况下车辆长时间以低于最低限速或超速行驶、车辆进入服务区休息、车辆故障等）会产生异常旅行时间，同时由于相邻收费站出行记录较少，某些周期内样本数量极少，甚至无有效样本。为减少离群数据和无效数据对后续建模带来较大误差，在计算某周期旅行时间前，需要对各周期内异常或无效数据进行修正，数据修正处理过程主要分为清洗和填补。

清洗异常数据的流程为：1)删除旅行时间为负值、零值、空值的数据记录；2)删除旅行时间大于一个自然日的数据；3)删除平均速度超过最大限速20%的数据；4)计算周期内旅行时间均值 µ和标准差δ，按 2δ 原 理删除旅行时间不在[µ−2δ,µ+2δ]范围内的数据；5)重复步骤4)直至剔除完所有不满足要求的数据后数据清洗完毕。

对无效数据的填补以k 路段在T周期下的旅行时间tk,T为例，若无法直接通过收费数据提取而得，则可以通过式（2）填补：

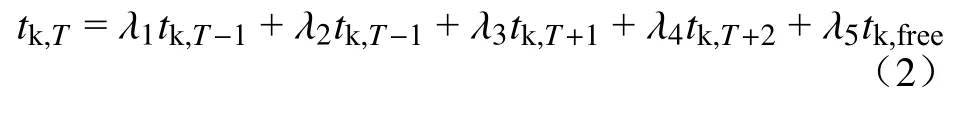
式中：λ1∼λ5为修正系数，可根据各路段实际情况取值，λ1+λ2+λ3+λ4+λ5=1；tk,free为k 路段自由流通行旅行时间。图2 给出了通道内某路段某天旅行时间修正前后对比情况，可见修正后的旅行时间波动范围有所减小，缺少有效数据的周期也有所修补。

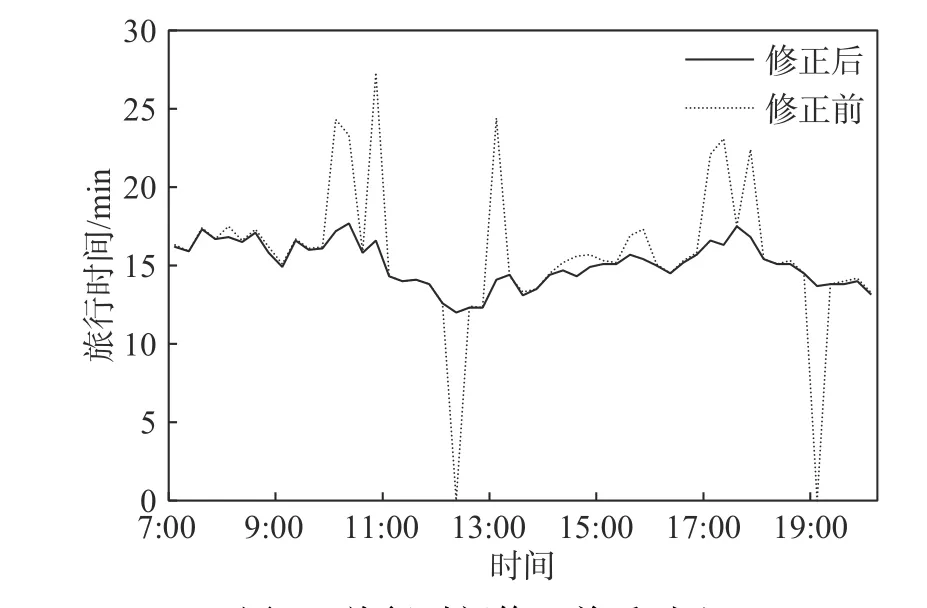
图2 旅行时间修正前后对比

2 基于随机森林的变量选择

2.1 备选变量构建

研究证实[10]，旅行时间除了具有时间序列时空自相关性以外，通常也受到天气条件、交通事件、路段施工、节假日等外部因素的影响；因此，本文将影响旅行时间的因素分为两类来构建备选变量，一类是前期旅行时间，另一类是外部影响因素。

2.1.1 前期旅行时间时空变量

由于旅行时间具有时间序列时空自相关性，因此需要同时从时间相关性和空间相关性两个方面进行分析，即除了考虑研究路段的前期历史旅行时间外，还需考虑相邻路段对该路段的影响。已有研究表明：对某一路段旅行时间影响最大的前期旅行时间是在其前10 个历史周期内；对某一路段旅行时间影响最大的相邻路段为该路段前后3 个路段内。图3 为空间变量关系图。

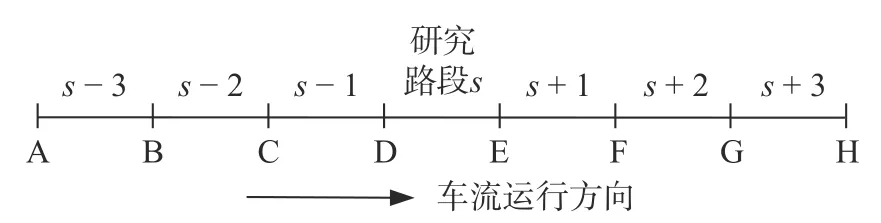
图3 变量的空间关系

图3 中，A—H 为收费站，研究目标路段s前后3 个路段（s±1,s±2,s±3）为本文考虑的前后3 个相邻路段空间变量。提取计算各路段旅行时间真实值，即可建立前期旅行时间时空变量，并按tX,Y命名规则为变量命名，其中X表示路段，Y表示历史周期。例如，变量tk,T−1代 表路段k 在T−1周期内的真实旅行时间，tk−1,T−5代表研究路段k 的上游最邻近的一个路段在T−5时刻的真实旅行时间。

2.1.2 外部影响因素

以往研究证实[6，8]，交通事件、路段类型及长度、天气和月份、周天、时段等均是影响旅行时间的重要外部影响因素。考虑到收费数据记录的信息有限，本文选择路段长度（lX）、月份（m）、周天（w）和时段（p）为备选变量。

对于路段长度lX（X=s,s±1,s±2,s±3），其为研究目标路段s及其相邻6 个路段共计7 个路段的站间距离。对于其余的外部影响因素变量，以研究通道及通道内某路段为例，统计分析该通道或路段在全年内收费记录数及旅行时间分布情况后对其进行分类。按交通流量将月份划分为两类：平峰交通流出行月1 月、3—5 月、10—12 月；高峰交通流出行月2 月、6—9 月。按交通流出行规律将周天分为两类，周一至周四为一类，周五至周日为另一类。按交通流出行特征将时段分为两类：高峰出行时段7—11、13—18 时；一般出行时段11—13、18—20 时。上述月份、周天、时段变量根据分类情况取值0 或1。

2.2 基于随机森林的变量选择

上述备选变量中包括70 个前期旅行时间时空变量和10 个外部影响因素变量。为防止变量间的交互作用和过多变量给后续建模带来过拟合风险，需从备选变量中筛选出影响旅行时间最重要的变量作为后续模型的输入。本文将使用随机森林（random forest,RF）算法来确定后续建模变量。RF 通过集成多棵决策树提升模型泛化能力和降低过拟合风险，其优势在于无需单独交叉验证测试数据集即可获得无偏误差估计，其本身能自然地避免变量间的交互作用，因此可以利用RF 的平均基尼系数下降值（mean decrease gini,MDG）对备选变量进行排序，变量MDG 越大说明该变量越重要。

使用RF 需确定各节点变量数和决策树数量，其中节点变量数取变量总数的平方根。本文节点数取值为9。决策树数量综合考虑其最小和最恒定袋外错误率来确定决策树数量取值。本文决策树数量取值为100，同时设置单颗决策树最大深度为10。

图4 给出了MDG 排前9 的变量计算结果。该图显示，变量ts,T−1的MDG 值最大，即预测路段的前一个周期旅行时间是影响旅行时间最重要的变量。同时，同一路段和相邻路段前几个周期的旅行时间也是影响旅行时间的重要变量。考虑到MDG 值前9 个变量基本涵盖了大部分的前期旅行时间时空变量和外部影响因素变量，故选择这9 个变量作为输入来构建旅行时间模型。

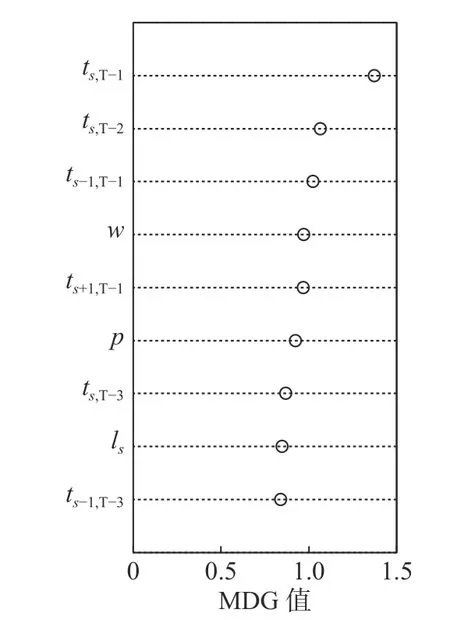
图4 变量MDG 值排序

3 基于BP 神经网络的旅行时间模型

3.1 BP 神经网络模型

BP（back propagation）神经网络能自主学习大量的输入与输出模式映射关系，且无需事前具体描述该映射关系，可借助优化函数，使用反向传播来不断调整网络节点的权重与阈值。BP 神经网络的结构包括输入层、隐含层和输出层，如图5 所示。

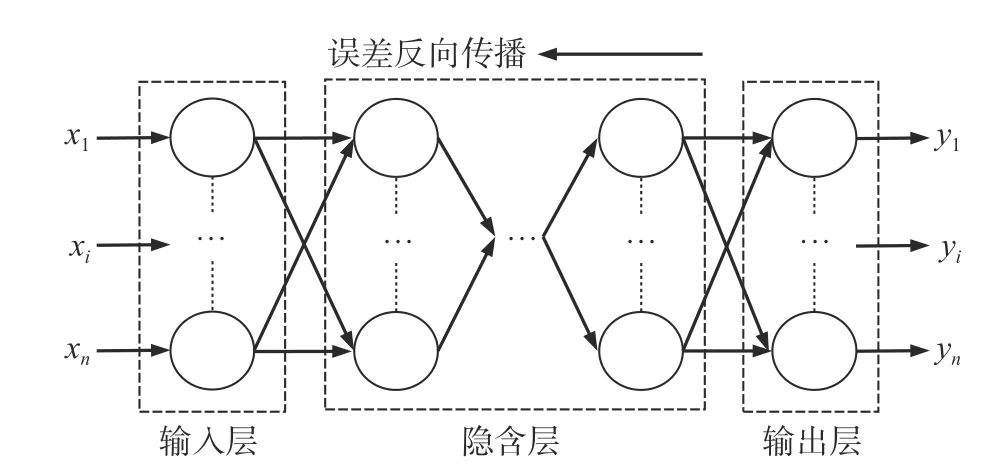
图5 BP 神经网络结构

通过建立输入xj与输出yj之间的映射关系实现预测。

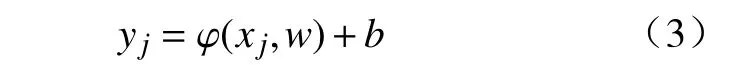
式中：xj、yj分 别为模型输入、输出，j=1,···i,···n；φ(·)为 映射关系；w表 示模型中各节点的权重；b为误差项。要使用BP 神经网络，需要确定神经网络的结构和模型中各种参数的取值，通过使用历史旅行时间对BP 神经网络的训练求得参数最佳取值，即可利用该模型预测旅行时间。

3.2 模型评价指标

采用均方根误差（e1）、平均绝对误差（e2）、平均绝对误差百分率（e3）作为模型预测能力的评价指标，计算公式分别为：

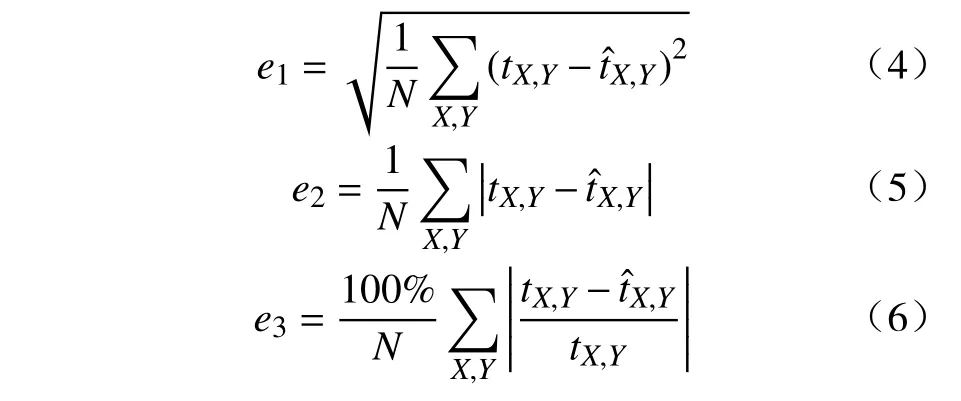
4 实验结果分析及讨论

对构建的真实旅行时间数据集按7:3 划分成训练集和验证集，使用Python 语言实现BP 神经网络旅行时间预测模型，并参考已有研究[11]确定模型结构。首先，易得模型的输入层节点数和输出层节点数，其中输入层节点数为变量数9，输出层节点数为1，即站间路段旅行时间值。然后，综合考虑旅行时间预测的复杂程度和模型训练所需计算力。本文设置隐含层的层数为3，并根据Kolmogorov定理设置隐含层节点数为 2q−1（其中q表示输入层节点数），即本文隐含层节点数为19。确定BP 神经网络结构后需要设置模型参数，本文采用Sigmoid函数作为激励函数，最大训练次数设置为10000，学习速率为0.01，误差目标值为0.001，后期可根据实验结果对参数进行调整。

选取通道内部分路段进行预测，根据周天分类，图6、7 给出了a 路段某周二、周六预测结果，图8、9 给出了b 路段某周三、周五预测结果，其中a 路段6.33 km，b 路段16.79 km。

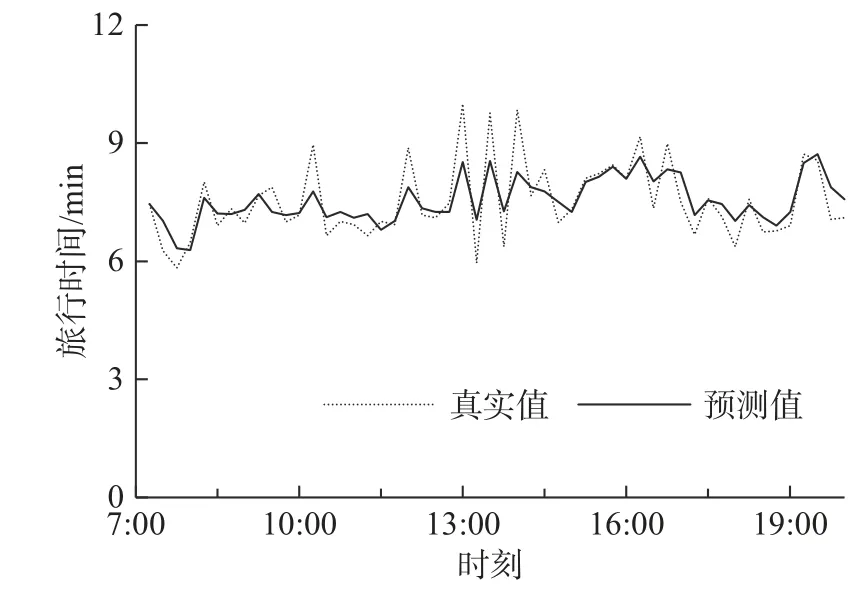
图6 路段a 某周二旅行时间预测结果

图7 路段a 某周六旅行时间预测结果

图8 路段b 某周三旅行时间预测结果

图9 路段b 某周五旅行时间预测结果

从图6—9 预测结果来看，模型在路段a 和路段b 下均表现良好，在两种周天分类情况下也都能实现旅行时间的预测。

针对通道内部分路段，通过式（4）—（6）计算所有预测结果的各项模型评价指标，以分析模型预测性能，路段a 与路段b 的预测结果见表1。

表1 显示：路段a 与路段b 在研究时段的高峰时段、一般时段和全时段内的预测误差均较低；全时段的平均绝对误差百分率分别为7.02%和5.76%，即模型在研究全时段内均能实现旅行时间预测。

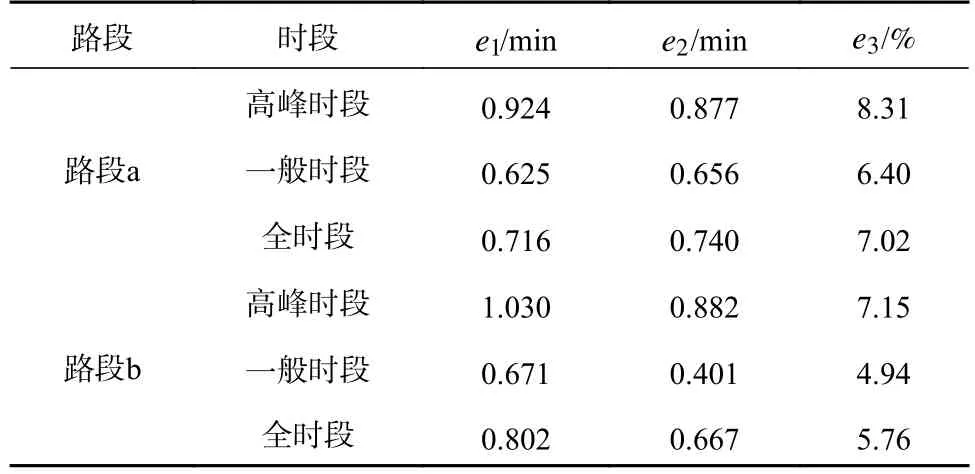
表1 模型误差

综上对周天分类的预测结果和各研究时段下预测结果的分析可知，本文建立的BP 神经网络模型能有效地预测高速公路旅行时间。模型预测结果能为交通管理者提供决策依据，以提高高速公路运营效率。

5 结论

1）使用高速公路联网收费数据建立了BP 神网络旅行时间预测模型，实验证明使用收费数据能够实现高速公路的旅行时间预测，模型对各时段的预测均表现出良好性能。

2）无需将所有影响旅行时间的变量全部输入到预测模型，经随机森林算法筛选出的重要变量，即可作为建立BP 神经网络模型的输入，实现旅行时间预测。

3）后续研究中，还可以考虑天气、道路线性等因素对旅行时间的影响，同时还可考虑交通事件对旅行时间的影响，进一步提高模型的适用性。