基于边缘检测和数字图像相关法的疲劳裂纹长度测量方法
2022-05-13黄心畏单晓锋高红俐王晨
黄心畏, 单晓锋, 高红俐, 王晨
(1.浙江工业大学 机械工程学院, 浙江 杭州 310023;2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室, 浙江 杭州 310023)
0 引言
节能、环保、轻量化是现代汽车工业目前的发展方向,先进高强钢(AHSS)是满足这一要求的汽车制造新材料,AHSS在具有高强度的同时也具有很高的韧性,可满足汽车制造轻量化和碰撞安全性的要求[1-3]。由于汽车主要的零部件在运行过程中不断受到交变载荷的激励作用处于动态服役状态,而非一次性加载破坏,单纯地用材料的静态拉伸性能无法全面描述其动态特性。用于汽车车身薄壁轻型结构的AHSS,在设计中不仅需要进行材料的疲劳寿命极限分析[4],还需要对其在交变载荷作用下裂纹的萌生、扩展特性进行分析[5-7],以实现对其疲劳寿命进行精准预测。为达到这个目的,则需要对疲劳裂纹扩展(FCG)过程中的裂纹长度进行精准的动态测量。
众所周知,对于塑性金属材料,在交变载荷的作用下会在裂纹尖端区域产生塑性变形,形成一个微小塑性区,并因此引起裂纹闭合现象,裂纹尖端闭合和塑性区内材料循环塑性变形行为是影响疲劳裂纹萌生和扩展的主要因素[8-10]。在采用一般相机所采集的裂纹图像上,闭合后的一小段裂纹和背景灰度分布几乎一致,采用基于灰度边缘检测技术的疲劳裂纹检测方法[11]很难将这段裂纹检测出来。对于具有相变诱发塑性(TRIP)效应的先进高强钢,在交变载荷的作用下,随着裂纹尖端塑性变形的产生,裂纹尖端塑性区内材料会发生残余奥氏体向马氏体的转变[12],从而使材料塑性和强度同时得到增强,导致其裂纹闭合现象更加明显[13-14],采用传统边缘检测技术进行裂纹长度测量和尖端定位误差更大。使用高放大倍率的显微摄像装置来采集裂纹图像进行相应的处理可实现疲劳裂纹高精度测量和尖端定位[15],但搭建这样一套显微裂纹图像采集与处理系统价格十分昂贵,而且需要进行复杂的显微图像匹配及相机运动精确控制。
本文在文献[11,16]研究基础上提出一种基于边缘检测和数字图像相关(DIC)技术相结合的AHSS疲劳裂纹长度高精度动态测量方法。该方法采用FCG试验相关标准[17]规定的标准尺寸制成具有和不具有TRIP效应的AHSS薄型紧凑拉伸(CT)试件,使用两个相机分别采集FCG试验过程中试件光洁面的裂纹图像与散斑面的散斑图像,通过灰度边缘检测方法在灰度图像中得到疲劳裂纹扩展路径,并对裂纹尖端进行初定位。再通过模板匹配技术将检测出的裂纹路径坐标映射到试件另一面的散斑图像,得到散斑图像中裂纹尖端初始坐标,并在裂纹尖端附近布置虚拟引伸计,使用DIC技术计算引伸计张量。由于裂纹穿过虚拟引伸计时,非连续裂纹表面的几何运动使得虚拟引伸计张开量增大,而对于裂纹未扩展到的区域,虚拟引伸计测点之间位移张开量较小,主要由弹性变形引起。根据这个特点拟合绘制出虚拟引伸计位移- 位置曲线,并对曲线进行分析即可精确定位裂纹尖端位置。本文方法为AHSS及类似材料FCG规律和裂纹尖端微细观断裂特性的测量和研究提供了一种新的试验和研究手段。
1 疲劳裂纹图像采集
1.1 试件疲劳裂纹图像特点
图1所示为CT试件开裂前、后的图像。图1中:DE为试件受力孔的中心线,在试件夹具安装对中的条件下,DE垂直于水平方向;A为预制裂纹的顶点,即疲劳裂纹的起点;B、C分别为预制裂纹加工拐点;F为疲劳裂纹尖端位置点;AF为FCG路径。
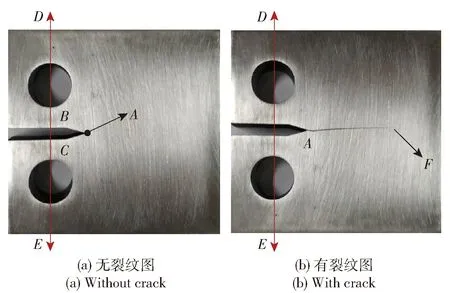
图1 无裂纹及带有裂纹试件Fig.1 Specimens with and without crack
一般情况下,疲劳裂纹长度的检测可采用各种边缘检测技术实现,但事实上,由于疲劳试验中的裂纹闭合现象和图像采集设备分辨率限制,导致采用一般的灰度边缘检测方法无法有效识别出末端的细微和闭合裂纹,如图2所示。
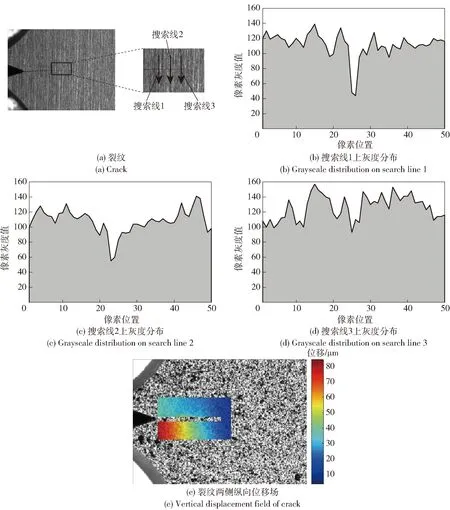
图2 细微裂纹及其灰度分布Fig.2 Gray level distribution of tiny crack
图2(a)为采用空间分辨率为6.73 μm/像素的相机所采集的FCG试验中的疲劳裂纹图像,在图2(a)裂纹末端区域放大图中可发现较明显的裂纹闭合现象。图2(b)、图2(c)、图2(d)为疲劳裂纹末端细微和闭合区域不同位置垂直搜索线1、2、3上的灰度分布图,在搜索线1、2上,像素灰度值分布存在明显落差,对于此处的裂纹使用一般的灰度边缘检测法即可很好地识别出裂纹。然而对于处于裂纹闭合段的搜索线3,其灰度分布较为均匀,基本在90~160的范围内波动,并没有明显的谷底出现,因此一般的边缘检测无法有效检测到这一段正处于闭合状态的裂纹,导致检测出的裂纹长度小于实际裂纹长度。
图2(e)为DIC计算所得疲劳裂纹周围的纵向位移场,分析可知:包括末端细微和闭合区域的裂纹两侧区域均具有显著的位移差,该位移差沿着裂纹扩展路径逐渐减小直至趋近于0 μm。本文所使用的RG-DIC算法[18]在传统DIC基础上进行了计算路径优化,针对显著不连续变形具有较高的计算精度,其使用1阶位移形函数表征位移[19],选择改进B样条插值函数[20]进行亚像素位移计算,亚像素精度可达0.000 1,配合本文所用相机完全可检测到裂纹闭合段的亚微米级(0.1~1 μm)[15]张口位移,进一步根据裂纹周围位移场变化规律即可准确测量裂纹闭合区域的长度。
1.2 疲劳裂纹图像采集系统
本文围绕谐振式疲劳试验机搭建试验平台,图像采集与测量系统原理图如图3所示。CT试件一面为漫反射处理后的表面,可进行灰度边缘检测,另一面为喷涂散斑漆的散斑表面,用于DIC计算。计算机控制试验机对试件进行常幅加载。试件两侧分别布置1台工业相机,2台工业相机的硬件参数、标定参数完全一致,保证裂纹图像与散斑图像的匹配。计算机通过图像处理软件向同步控制器发出拍照信号,同步控制器触发2台相机同时拍照,采集图像并将其传输回计算机。再通过图像处理软件对裂纹图像与散斑图像分别进行灰度边缘检测与DIC计算,从而实现裂纹长度的精确测量。
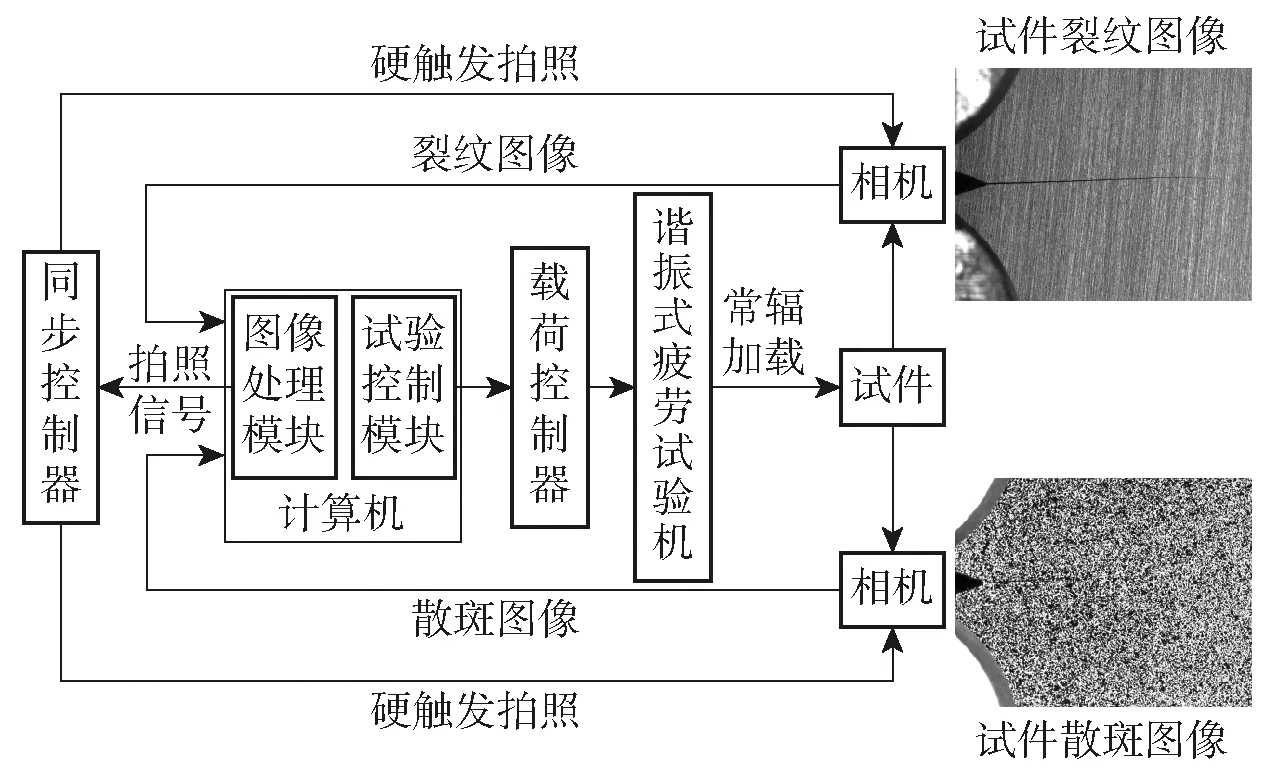
图3 疲劳裂纹图像采集系统原理框图Fig.3 Block diagram of fatigue crack image acquisition system
本文采用文献[11]中的高速开关法进行图像采集,使用的相机镜头为维视智造科技股份有限公司生产的MV-UG300U3M型号相机与BT-118C3520MP5型号定焦镜头。
2 结合边缘检测与DIC的疲劳裂纹长度精确测量方法
2.1 测量方法流程
如图4所示为边缘检测与DIC相结合的裂纹长度测量流程图。具体步骤如下:
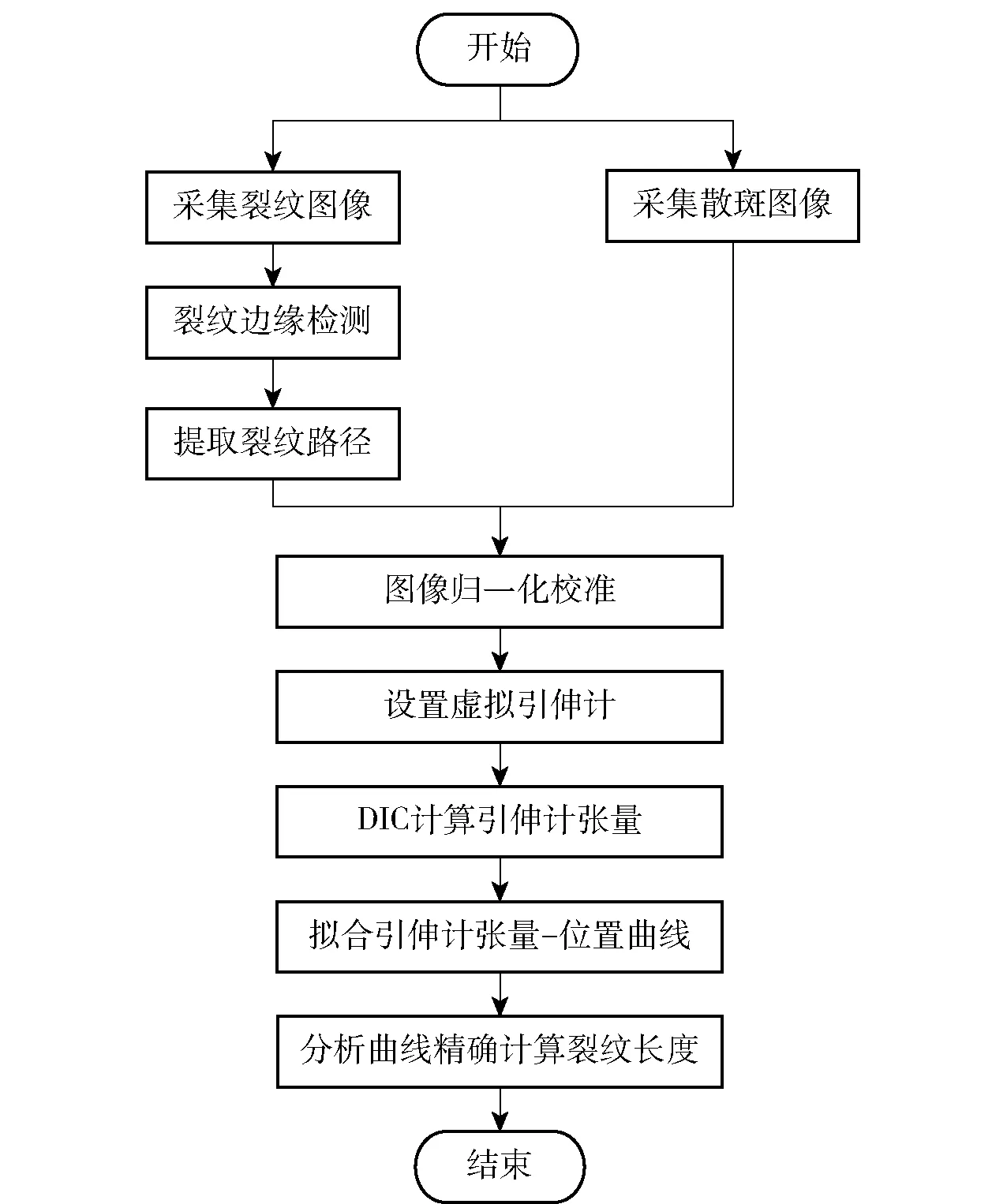
图4 疲劳裂纹长度精确测量方法Fig.4 Flowchart of accurate measurement of fatigue crack length
步骤1采集裂纹图像与散斑图像。
步骤2裂纹边缘检测:使用文献[11]中的自适应阈值边缘检测方法定位裂纹起点,并对裂纹进行检测,初步提取裂纹路径及计算裂纹的亚像素长度。
步骤3图像归一化校准:选择预制裂纹作为模板,通过模板匹配技术将提取出的裂纹路径坐标映射到散斑图像中,从而获取散斑图像中的裂纹扩展路径以及裂纹尖端初位置。
步骤4设置虚拟引伸计:根据融合的裂纹路径,在裂纹初尖端两侧布置若干个虚拟引伸计。
步骤5DIC计算引伸计张量:使用RG-DIC算法[18]计算引伸计张量。
步骤6拟合引伸计张量- 位置曲线:引伸计张口作为纵坐标,引伸计横向坐标作为横坐标,拟合出张量- 位置曲线。
步骤7分析曲线精确计算裂纹长度:计算张量- 位置曲线拐点,得到裂纹尖端横坐标进而计算裂纹长度。
在上述步骤中,图像归一化校准与基于DIC虚拟引伸计的尖端定位是本方法的关键,下文将重点介绍。
2.2 裂纹路径与散斑图像的归一化校准
由2.1节分析可知,在使用边缘检测方法检测出裂纹后,需要将裂纹路径坐标映射到散斑图像中,根据裂纹尖端的初位置布置虚拟引伸计。由于裂纹图像与散斑图像不是由同一个相机采集得到的,无法保证2幅图像的像素坐标系完全对应。因此首先需要通过模板匹配技术计算裂纹图像与散斑图像的仿射变换矩阵,将裂纹图像中的裂纹路径经仿射变换即可得到散斑图像中对应的裂纹路径。
图5所示为图像归一化校准过程示意图。首先选取裂纹图像中的预制裂纹作为模板,在散斑图像中进行模板匹配,计算得到裂纹图像与散斑图像的仿射变换矩阵。将识别得到的裂纹路径与仿射变换矩阵进行计算,得到散斑图像中对应的裂纹路径与裂纹尖端初坐标,为后续布置虚拟引伸计提供参考坐标。

图5 图像归一化校准示意图Fig.5 Diagram of image normalization calibration
本文使用基于零均值归一化互相关函数的模板匹配法计算裂纹图像与散斑图像的仿射变换矩阵:
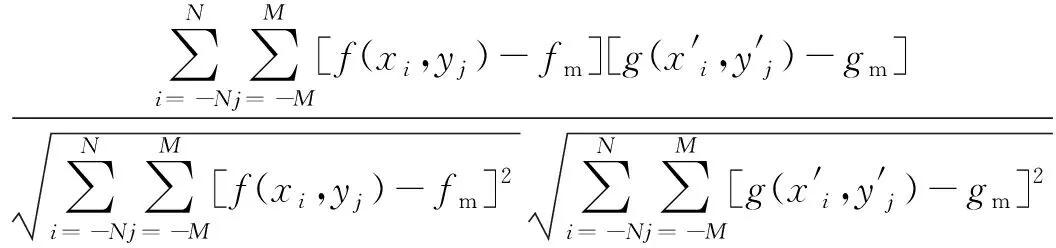
(1)
(2)
(3)
式中:CZ为互相关系数;模板图像尺寸高×宽为(2M+1)*(2N+1);i、j为像素点在模板图像相对于图像中心的位置;f(xi,yj)为模板图像中坐标(xi,yj)像素的灰度;g(x′i,y′j)为目标图像子图中坐标(x′i,y′j)像素的灰度;fm和gm分别为模板图像和目标图像子图的灰度平均值。
由1.2节可知:散斑图像与裂纹图像在尺度上完全相同,意味着模板与目标不存在缩放;同时散斑图像与裂纹图像是同一块试件的两侧,因此不存在错切、翻转。结合上述分析可知,裂纹图像中的模板与散斑图像中的目标仅存在刚体变换,即平移与旋转,可通过以下5个参数描述:Txc为裂纹图像中模板的x轴坐标,Tyc为裂纹图像中模板的y轴坐标,Txs为散斑图像中目标的x轴坐标,Tys为散斑图像中目标的y轴坐标,α为散斑图像中目标相对于x轴的旋转角度。其中Txc、Tyc已知,通过零均值归一化互相关函数模板匹配计算Txs、Tys、α,再使用仿射变换矩阵表示上述5个参数:
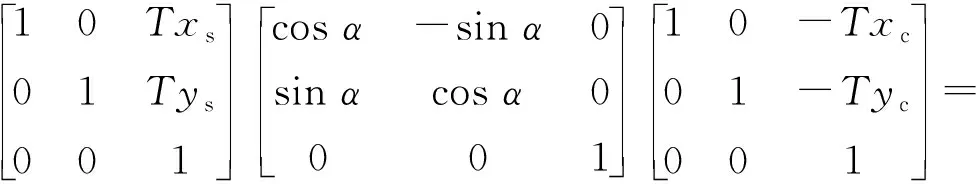
(4)
再将裂纹路径上的每个像素点与变换矩阵相乘即可得到散斑图像中对应的裂纹路径:
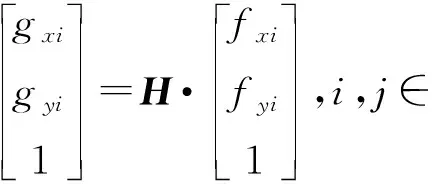
(5)
式中:gxi、gyj为散斑图像中对应的裂纹路径坐标;fxi、fyj为裂纹图像中裂纹路径上的像素点坐标。
2.3 基于DIC虚拟引伸计的裂纹尖端定位
图6所示为DIC基本原理[21],变形前的图像为参考图像,变形后的图像为目标图像。图6中,P(x0、y0)、Q(xi、yj)为参考子区中心点与参考子区中任意一点;P′(x′0,y′0)、Q′(x′i,y′j)为所匹配到的目标子区中心点与目标子区中任意一点。它们之间的关系可用以下公式表示:
x′0=x0+u
(6)
y′0=y0+v
(7)
x′i=xi+ξ(xi,yj)
(8)
y′i=yi+η(xi,yj)
(9)
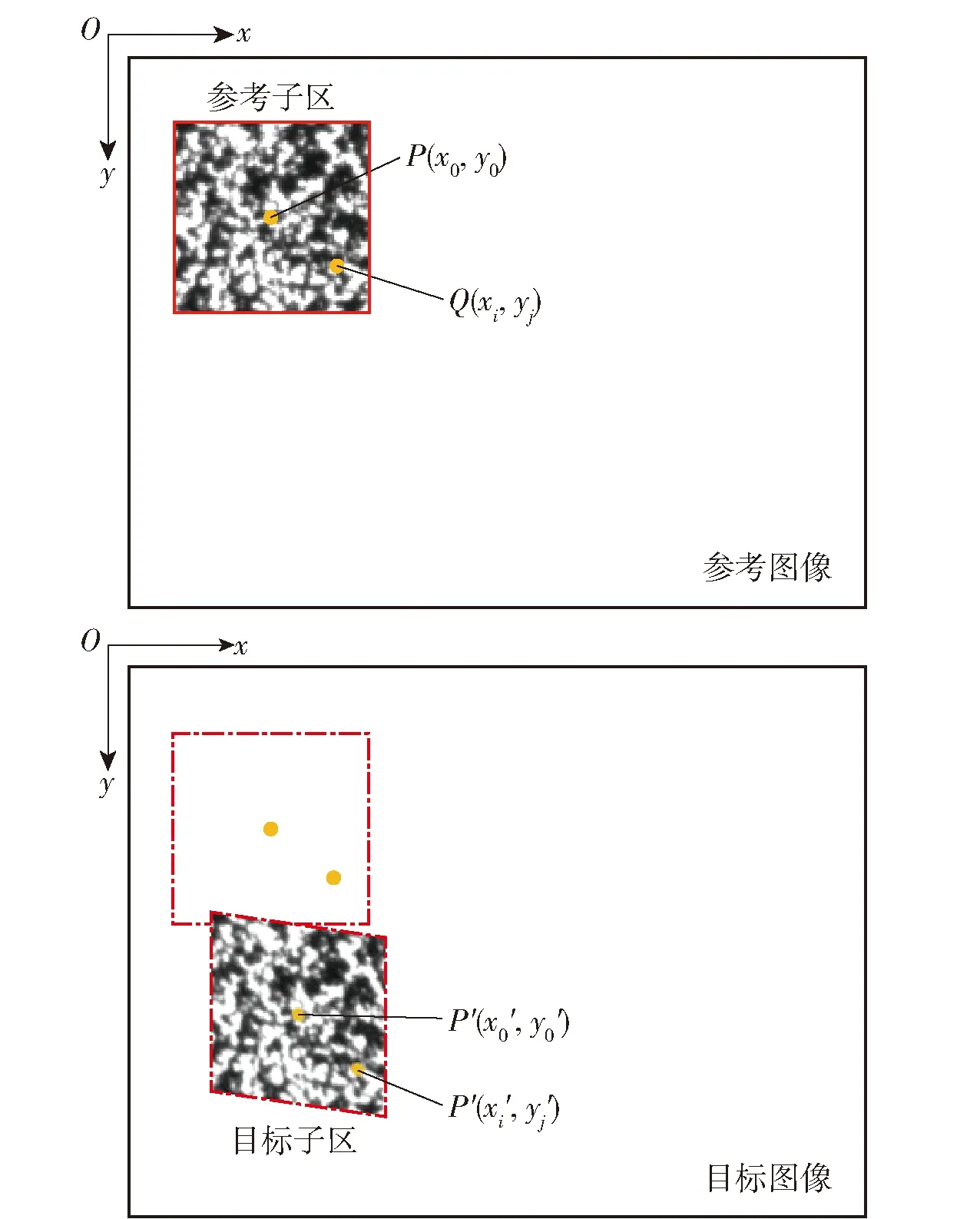
图6 DIC原理图Fig.6 Schematic diagram of DIC
式中:u、v为目标子区中心点与参考子区中心点的偏移量;ξ(xi,yj)、η(xi,yj)为用于表征目标点与参考点相对位置关系的形函数。首先将图像划分成各个子区,再使用相关性函数定位与参考子区匹配的目标子区,即可得到子区的中心偏移量u、v。通过1阶形位移函数即可计算子区内所有点的偏移量:
ξ(xi,yj)=u+uxΔx+uyΔy
(10)
η(xi,yj)=v+vxΔx+vyΔy
(11)
式中:ux、uy为目标子区中心与参考子区中心x轴方向偏移量沿x轴、y轴方向的偏导数;vx、vy为目标子区中心与参考子区中心y轴方向偏移量沿x轴、y轴方向的偏导数;Δx=xi-x0,Δy=yi-y0。
虚拟引伸计技术[22]是基于DIC实现的,在图像中选择2个像素点构成一对虚拟引伸计。这2个点分别作为2个子区的中心点,选择适合的子区尺寸后使用DIC计算2个像素点的位移,将位移相减即可得到引伸计张量。
由于边缘检测只能初步得到裂纹的初尖端,而实际尖端位置在初尖端向前大约0~0.5 mm处。为准确测量疲劳裂纹的长度,本文在初尖端延伸线两侧布置虚拟引伸计,使用RG-DIC算法计算引伸计张开量,根据引伸计张量变化趋势精准定位裂纹尖端。图7所示为虚拟引伸计布置示意图。
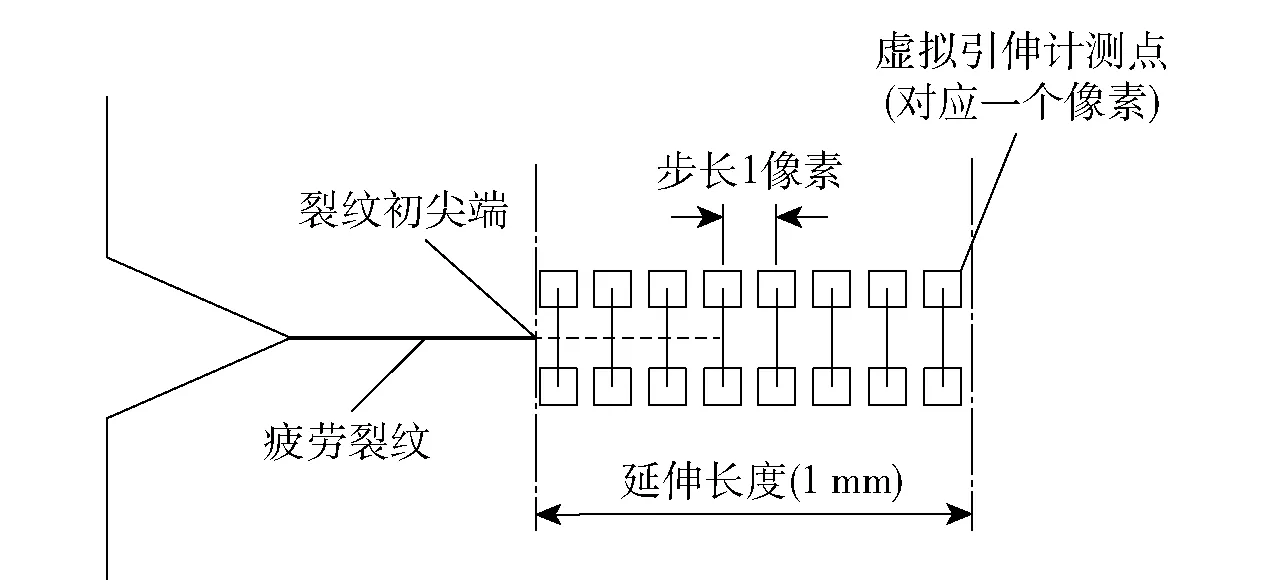
图7 虚拟引伸计的布置Fig.7 Arrangement of virtual extensometer
在映射到散斑图像中的裂纹路径前端向前做1 mm延伸线,并在延伸线两侧以1像素步长均匀布置若干个虚拟引伸计,通过DIC计算即可得到每一对虚拟引伸计的张量如下:
[d0,x0],[d1,x1],…,[di-1,xi-1],[di,xi]
(12)
式中:di为各个引伸计张量;xi为各个引伸计的x轴像素坐标。为方便数据拟合,做如下变换:
[d0,0],[d1,Δx1],…,[di-1,Δxi-1],[di,Δxi]
(13)
式中:Δxi=xi-x0,这样数据的自变量将从0开始递增,方便拟合计算。
选择5阶傅里叶拟合法对数据进行拟合,函数模型如(14)式所示。相比于其他拟合方法,该方法得到的拟合函数在所给数据区间内可得到0.999以上的确定系数(R-Square)与0.01以下的均方根(RMSE),且导数计算简单,因此选择此拟合法对引伸计位置- 张量数据进行拟合。
(14)
式中:ω、a0、ai、bi均为傅里叶拟合参数。
图8所示为拟合曲线趋势示意图,对曲线做2次求导后,计算2阶导数曲线上的极大点即可得到裂纹尖端的相对位置xp,在图像坐标上的绝对位置则为xp+x0,将绝对位置减去裂纹起点即可精确计算出裂纹的长度。
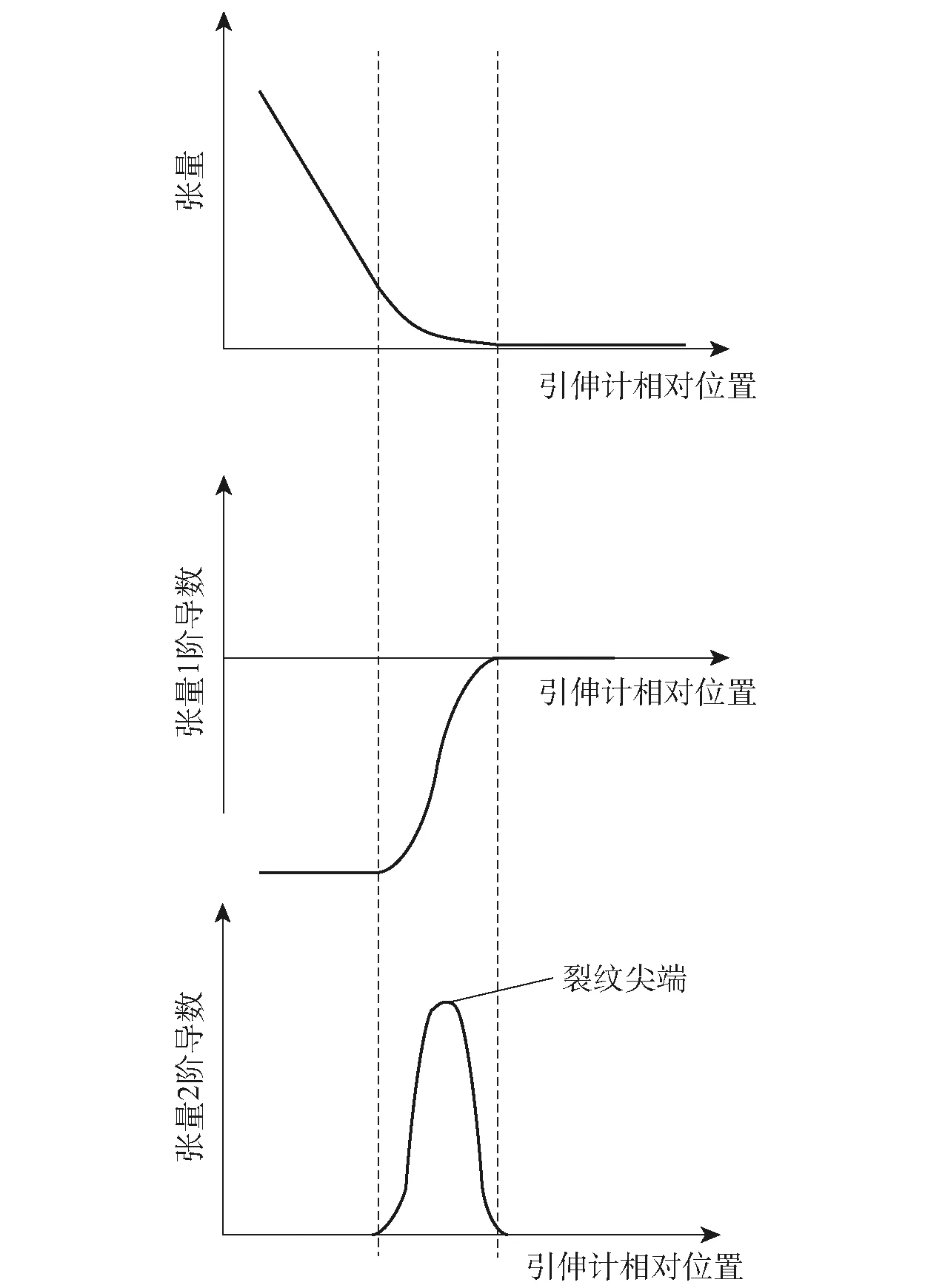
图8 不同位置引伸计张量曲线Fig.8 Displacement opening curves at different positions
3 试验及结果分析
3.1 试验方法
本文所使用的试验平台如图9所示,使用天水红山试验机有限公司生产的PLG-100电磁谐振式高频疲劳试验机,相机镜头使用维视智造科技股份有限公司所生产的MV-UG300U3M工业相机与BT-118C3520MP5定焦镜头,参数如表1所示。

图9 谐振式疲劳试验系统Fig.9 Resonant fatigue test system

表1 相机镜头参数
为验证本文方法对闭合裂纹段的检测效果,选择具有显著裂纹闭合的TRIP材料与裂纹闭合不显著的材料进行对照试验。由于裂纹闭合仅发生在塑性区,塑性区尺寸是影响裂纹闭合段长度的关键因素之一。根据塑性区尺寸计算公式[6],塑性区尺寸受材料屈服强度影响,因此选取的两种材料还需要有接近的屈服强度。在现有报道的TRIP钢研究文献[23-24]中,许多学者选择TRIP钢与双相钢进行对照研究。本文选择TRIP600与DP600两种材料,它们具有接近的屈服强度,且TRIP600的金相组成为铁素体、贝氏体以及残余奥氏体,由于包含残余奥氏体因此具有TRIP效应,而DP600的金相组成为铁素体、马氏体[25],并没有残余奥氏体,是较理想的试验对象。
如图10所示,使用符合FCG试验相关标准[17]的标准尺寸,将上述两种材料制成CT试件进行试验。为保证所采集的裂纹图像具有均匀的亮度,将试件一面打磨成漫反射表面用于裂纹边缘检测,另一面喷涂散斑制成散斑表面用于DIC计算。众所周知,散斑图像质量是影响DIC计算精度的关键之一,本文使用多种评价指标[26-27]对散斑图像进行综合质量评价,保证制备的散斑具有较高质量,使DIC计算具有较好的精度。
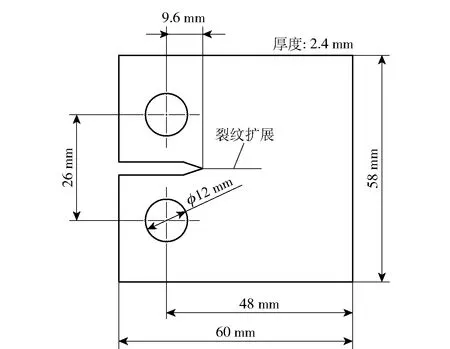
图10 CT试件尺寸图Fig.10 Dimension drawing of CT test specimen
为测得试件实际物理裂纹长度,需要对系统进行标定。首先将2台相机镜头到试件的距离通过云台设置为100 mm,再使用文献[28]的标定方法分别对2台相机进行标定。不断微调相机的位置,直到2台相机的空间分辨率趋近一致。最终得到2台相机的物理尺寸与像素的比例关系为6.73 μm/像素。
标定完成后则开始对本文方法进行验证试验。为验证本文方法可有效检测出裂纹闭合段,先进行裂纹长度测量试验。为进一步探究本文方法测量精度与优势,再进行测量精度试验,对两种材料分别使用本文方法与边缘检测法进行测量,做对比分析。具体试验与结果分析将在3.2节详细阐述。
3.2 裂纹长度测量试验
取一块TRIP600试件进行疲劳扩展试验,正弦交变载荷参数为:平均载荷4.84 kN,最大载荷6.67 kN,最小载荷3.01 kN。在试验过程中采集不同长度下的裂纹图像,使用本文方法在线处理。部分测量结果如图11所示。图11中包含4组图像,每组图包含3幅图,上中下分别为裂纹原图、裂纹尖端初定位图、最终检测结果图。从图11中可以看出整体检测效果较好,在肉眼可见范围内的裂纹都可以有效检测到。但是最终检测标记的裂纹尖端相比初定位标记的尖端有所延伸,表明该延伸段则为裂纹闭合段。

图11 裂纹长度测量结果Fig.11 Measured results of crack length
为进一步验证延伸段长度是否与实际裂纹闭合段长度接近,在获取最后一组裂纹数据后,将设备停机,并将载荷设置为最后一组裂纹图像下试件所受载荷,保持前后载荷一致。
图12所示为裂纹尖端初定位后的虚拟引伸计布置图。图13所示为DIC计算得到的引伸计张量- 位置拟合曲线及其1阶、2阶导数曲线。由图13(a)可知,张量突变点在50~80像素位置之间,在此区间范围内2阶导数极大点进行求解。最终裂纹尖端位置在59.834 3像素处,最终尖端位置比初尖端位置延伸了402.7 μm。

图12 虚拟引伸计布置局部图Fig.12 Layout of virtual extensometers
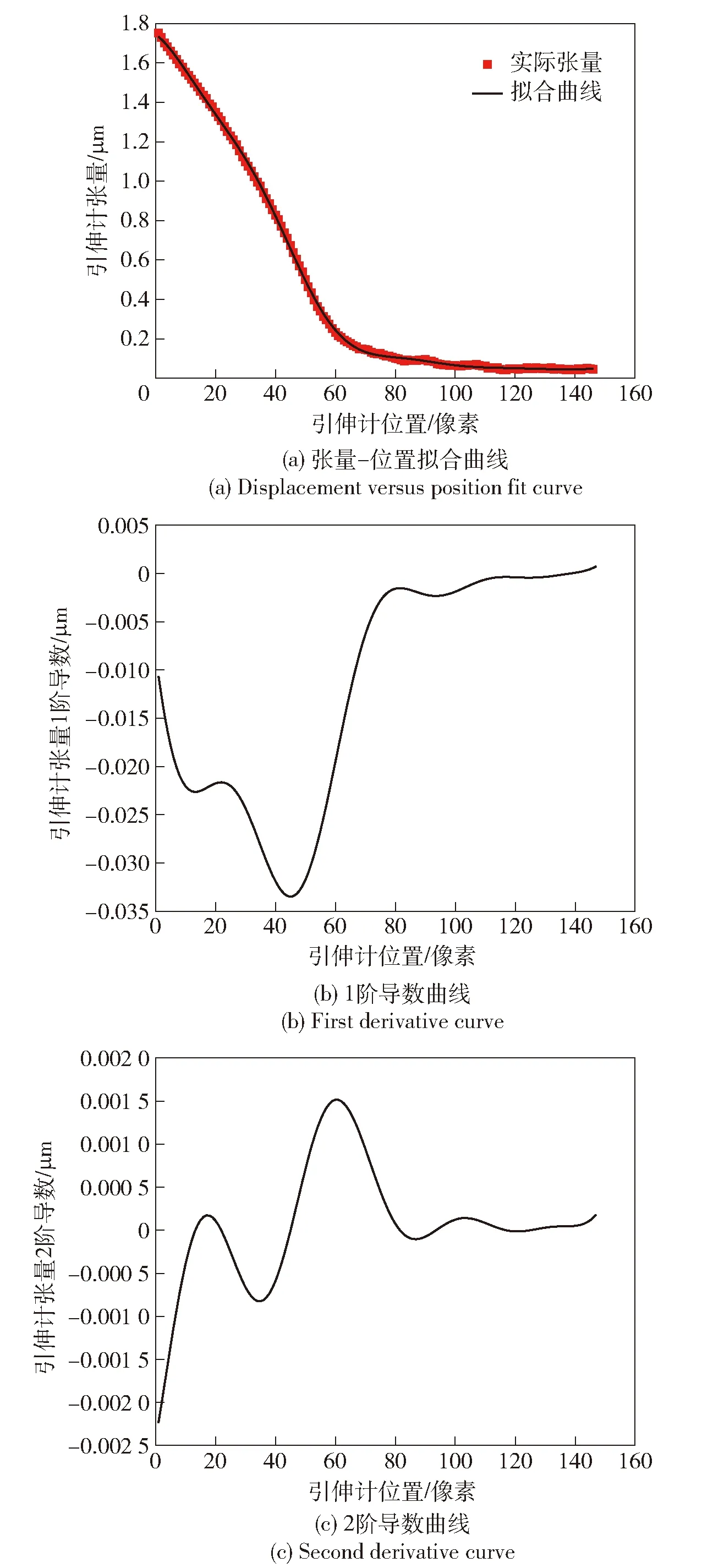
图13 虚拟引伸计张量- 位置曲线Fig.13 Displacement versus position curve for DIC virtual extensometers
使用显微相机对此时静载下的试件裂纹尖端进行拍摄,将拍摄得到的图像与图13获取的裂纹数据进行对比,如图14所示。图14中,图像上方为初定位的结果图,其中绿色×代表裂纹初尖端位置;下方为显微相机拍摄的图像,可见裂纹初尖端位置前有一段已经闭合的裂纹没有被检测到,闭合裂纹长度大概在400 μm左右,与图13中计算得到的延伸段长度接近,表明本文方法确实可以有效检测裂纹闭合段。
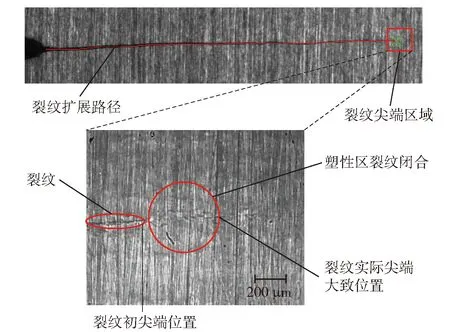
图14 试件表面裂纹检测效果Fig.14 Detected results of surface crack of test specimen
3.3 测量精度试验
3.2节的试验仅只能验证本文方法可检测到裂纹闭合段,但是无法表明测量精度,因此进一步对本文方法精度进行检验。取由TRIP600与DP600制成的标准CT试件进行疲劳试验,正弦交变载荷参数为:平均载荷4.72 kN,最大载荷6.52 kN,最小载荷2.92 kN。在裂纹扩展过程中试验系统的加载频率随着系统固有频率逐渐减小,并保持试验载荷不变。
3.3.1 TRIP600试件进行试验
在不同裂纹长度下使用边缘检测法与本文方法进行测量。然后停机将试件取下,使用测量显微镜(测量精度为±0.1 μm)测量裂纹长度,测量完毕后将试件重新放入试验机,以相同参数起振,继续疲劳试验。试验结果如表2所示。以测量显微镜测得的数据为参考值,使用边缘检测方法的测量误差为407.5 μm,使用本文方法的测量误差为7.8 μm,精度具有较大提升。
图15所示为两种测量方法误差趋势(TRIP600)。由图15可知:随着裂纹扩展,两种检测方式的相对误差都变小,之后都趋于稳定;边缘检测方法的相对误差波动较大,表明对于较短的裂纹,边缘检测方法不能满足较高精度的测量,而本文方法的相对误差波动较小,其对于短裂纹的适应性较好;随着裂纹扩展,绝对误差略有减小,总体上没有太大波动,边缘检测测量的绝对误差在350 μm上下波动,本文方法则在7 μm左右波动;本文方法得到的测量误差与边缘检测方法得到的测量误差不在一个数量级,对于TRIP600,本文方法具有较大优势。
3.3.2 DP600试件重复对照试验
再取DP600试件重复上述试验进行对照。结果如表3所示。由表3可见:对于DP600,使用边缘检测方法的测量误差为21.5 μm,与TRIP600相比误差较小,这是因为DP600的塑性区较小,闭合的裂纹较短所造成的;使用本文方法的测量误差为7.6 μm,与TRIP600相近。对比分析图15、图16可知,两种材料的误差曲线趋势大致相同,但是分析下DP600的误差曲线可知,本文方法虽然较边缘检测法测量误差较小,但二者的测量误差已经在同一个数量级。可见本文方法不论是对于TRIP600还是DP600都具有较高的测量精度,测量结果更加稳定可靠,而边缘检测方法得到的结果对于不同材料则存在较大的波动。
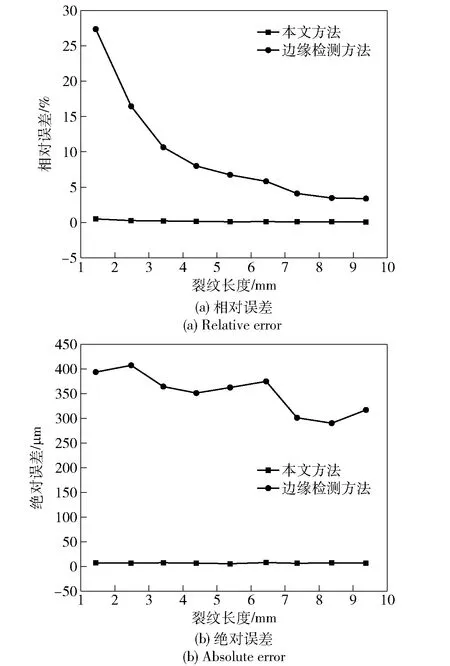
图15 两种测量方法误差趋势(TRIP600)Fig.15 Error trend of two measurement methods (TRIP600)
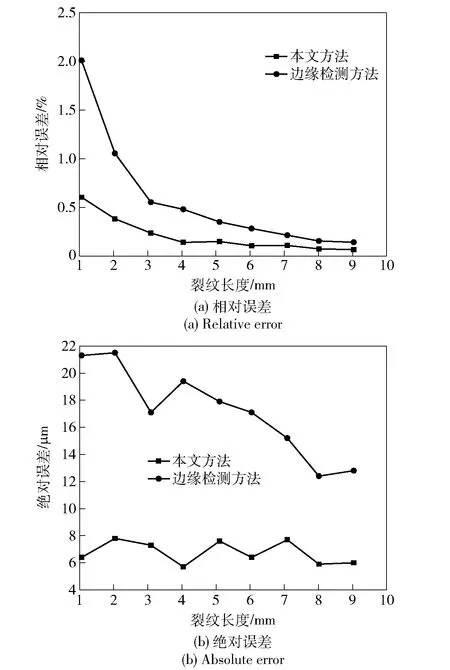
图16 两种测量方法误差趋势(DP600)Fig.16 Error trend of two measurement methods(DP600)
对绝对误差曲线如图15(b)、图16(b)进行分析可知,不论是TRIP600还是DP600,边缘检测方法得到的测量误差随裂纹增长而减小,表明裂纹长度对边缘检测方法检测结果有较大影响,对于短裂纹测量误差较大;而本文方法得到的测量误差则不会受到裂纹长度的影响。
3.3.3 两组试件不同载荷条件下试验
由于裂纹闭合张口大小受载荷影响较大,为证明本文方法稳定性,再取两组试件在不同载荷条件下进行试验:第1组保持相同平均载荷,改变载荷幅度;第2组保持载荷幅度,改变平均载荷。得到的试验数据与表1、表2具有相同规律,本文方法仍可达到8 μm的测量精度,进一步表明了本文方法测量结果的稳定性。
结合表2、表3分析可知,不论是边缘检测法还是本文方法,其检测得到的裂纹长度大都小于参考值,表明对于微细观层面的裂纹检测,本文方法还具有一定的局限性。进一步对误差来源进行分析可知,造成误差的因素有:
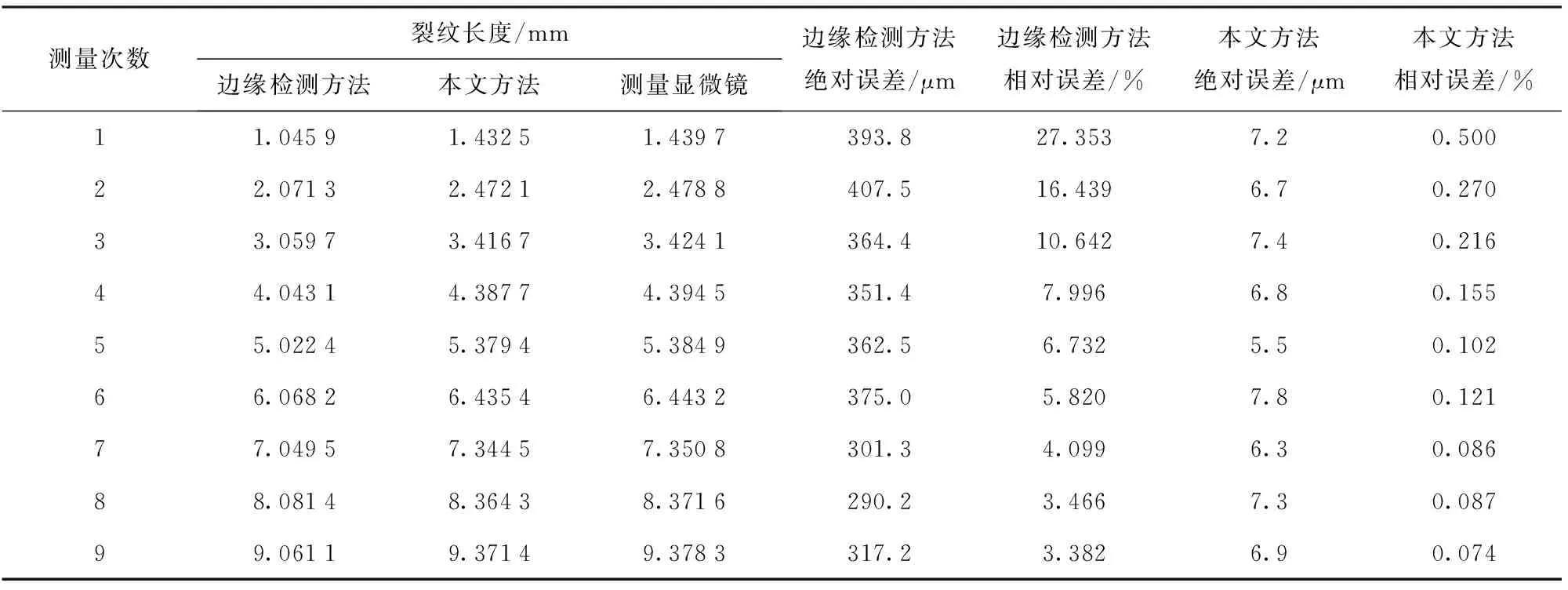
表2 不同测量方法得到的裂纹长度对比(TRIP600)
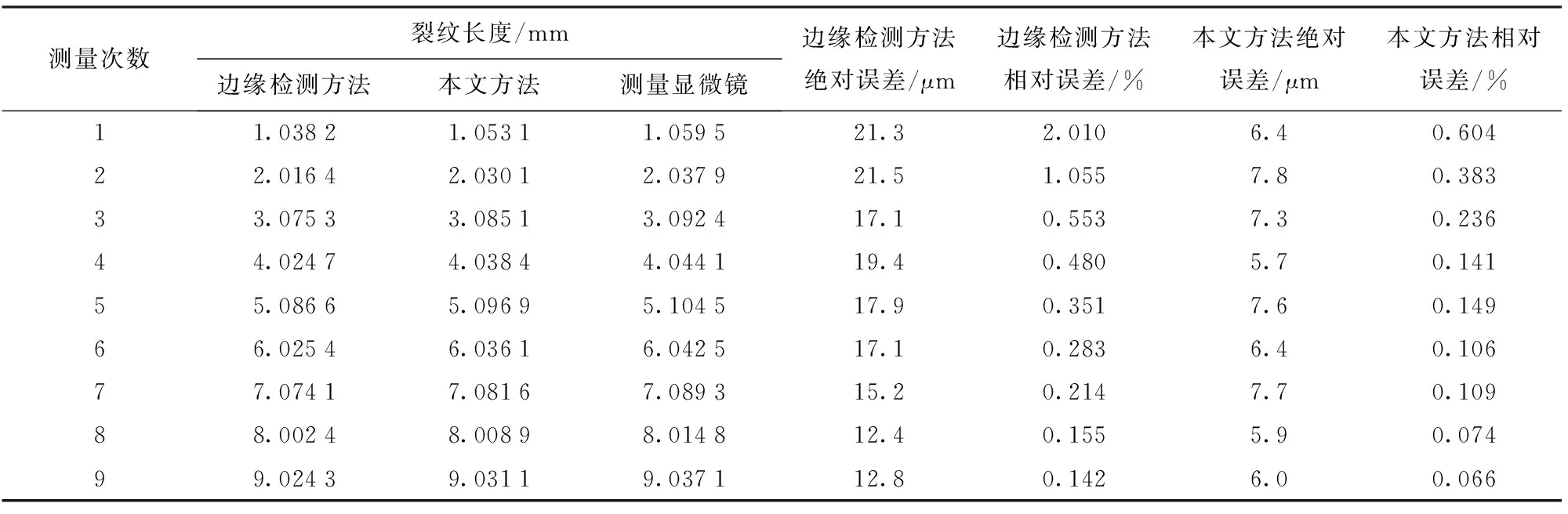
表3 不同测量方法得到的裂纹长度对比(DP600)
1)喷涂的散斑质量:DIC是基于散斑图像进行位移场计算的,而人工喷涂的散斑质量不稳定,导致DIC计算结果不同从而引起测量误差。
2)算法误差:本文使用的RG-DIC算法本身存在的测量误差引起测量误差。
3)引伸计张量- 位置曲线拟合法:曲线拟合法只能近似表征引伸计张量- 位置实际趋势,通过分析曲线特征点并不等于实际的特征点,引起测量误差。
4)视觉系统标定方法:所使用的标定方法本身存在标定误差,导致将像素尺寸转换成理论尺寸时产生误差。
4 结论
1)在宏观条件下,本文方法相比于边缘检测方法精度较高,测量精度达8 μm,可有效测量出闭合的裂纹,边缘检测方法则容易忽略闭合裂纹段。
2)对于具有显著裂纹闭合现象的材料(以TRIP600为例),本文方法较边缘检测法具有显著优势,可将精度提高一个数量级。而对于裂纹闭合现象不明显的材料(以DP600为例),本文方法仍可保持同样的精度。
3)本文方法测量精度不受裂纹长度影响,对于短裂纹仍能保持精度。
综上所述,本文方法测量精度高,结果稳定可靠,为进一步研究AHSS材料疲劳扩展机理以及扩展参数的测量奠定了理论与试验基础,具有较好的理论价值与应用价值。
