时频数据驱动的典型复杂供输机构健康状态软测量方法

张钢， 梁伟阁， 佘博， 田福庆

(1.海军工程大学 兵器工程学院， 湖北 武汉 430033； 2.海军大连舰艇学院 导弹与舰炮系， 辽宁 大连 116018)

0 引言

复杂供输机构是特种装备的重要组成部分，其可靠性和稳定性直接影响特种装备功能的发挥，如火炮供输机构，直接影响弹药的运动状态[1]，且其运动过程伴随有猛烈的冲击、振动等，力学环境十分复杂，对此复杂供输机构进行状态监测已经成为装备健康管理领域关注的焦点问题[2]。

目前，复杂机械设备的健康状态评估方法主要分为机理模型和数据驱动两类。基于机理模型的健康状态评估方法通过建立机械设备失效机理的数学模型[3-5]描述性能退化过程[6-8]。但是，由于类似火炮供输机构的复杂机械设备，运动过程复杂、力学环境恶劣、性能退化机理复杂多变，难以建立准确的机理模型反映其健康状态。

随着传感器技术的不断发展，数据驱动的健康状态评估方法成为研究热点[9-11]。但是传感器测得的振动信号数据往往只能反映机械设备某一方面的特征，并不能直接反映其健康状态。汤健等[12]提出一种适用于旋转机械设备状态监测的软测量技术，通过传感器测量旋转机械运行数据，并提取机械设备多方面的特征信息，构建这些特征信息的融合模型，从而得到能够有效反映其健康状态信息的软测量模型。概括而言，软测量技术主要包括特征提取[13]、建立软测量模型[14]、模型评价[15]等部分。

目前的研究均是基于公共数据集，研究结果对复杂供输机构的测量不具有普适性，潘宏侠等[16]采集火炮供输机构振动信号，利用同步压缩时频变换分析得到反映不同运行状态的二维时频图像，对图像进行灰度化处理后，提取其纹理特征作为输入，搭建基于模糊聚类的供输机构软测量模型，有效识别机构不同健康状态。张航等[17]提出一种基于多分辨奇异值分解与灰色理论的火炮供输机构软测量模型，有效区分火炮供输机构不同的健康状态。席茂松等[18]对火炮供输机构振动信号进行多尺度分解，提取分量信号信息熵作为特征，利用概率神经网络搭建软测量模型，有效识别供输机构早期健康状态变化情况。然而，上述研究重点在火炮供输机构健康状态识别，性能退化阶段健康状态的定量变化情况有待进一步研究。同时，在特征提取过程中需要依赖一定的专家经验。

针对以上问题，本文拟采集供输机构振动信号，提取振动信号时频图像，利用深度卷积网络搭建软测量模型，定量描述振动信号与供输机构健康状态关系，并在复杂供输机构上进行试验验证，以期为供输机构健康管理提供一定的理论参考。

1 软测量理论介绍

1.1 连续小波变换

机械设备健康状态退化过程中，振动加速度信号存在非平稳特征。时频分析能够有效表征非平稳信号时频特征，可利用连续小波变换提取非平稳振动信号的特征，模型为

(1)

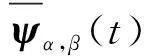
1.2 卷积神经网络

典型的卷积神经网络主要包括3层：卷积层、池化层和全连接层。首先，卷积神经网络通过堆叠的卷积层和池化层提取原始图片的二维特征；然后，将二维特征展平成一维特征向量；最后，将一维特征向量输入到全连接层，得到输出数值。

卷积层中，卷积核与前一层的特征图进行卷积操作，然后将卷积结果输入到激活函数，构建当前层的特征图，即

(2)

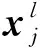
利用展平层将通过堆叠卷积层和池化层构建的特征图展平成一维特征向量。将该特征向量输入到全连接层中，得到最终输出值，即

(3)

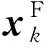
1.3 基于变分推断的模型不确定性估计理论

对于1.2节构建的卷积神经网络，本文采用dropout正则化方法防止网络训练过拟合。假设网络权重随机变量ω服从高斯先验分布，X表示给定的训练数据，Y表示对应的输出。通过贝叶斯理论可得随机变量ω的后验概率分布为

(4)

随机变量ω包括深度学习网络中所有可学习得到的参数，包括卷积层的内核和偏置项，全连接层的权重和偏置项。

(5)

式中：y*表示预测输出值；x*表示网络输入值；q(ω) 为权重ω的取值概率；q*(ω)为使KL散度最小的数值。因此，不难得出，卷积神经网络的优化目的就是使得KL散度最小，即相当于最大化证据下边界。因此，卷积神经网络的目标函数可以表示为

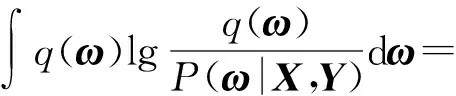
(6)

式中：xr和yr分别为第r个训练数据和对应的输出值。

(6)式右边第1项可以采用蒙特卡洛积分法求解，可得

(7)

(8)

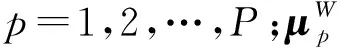
通过分析(7)式、(8)式可知，卷积神经网络模型的输出值yr随采样权重ω的变化，可以看做是随机删除权重矩阵中的某些行，这与深度学习网络中的dropout过程是一致的。因此，深度学习网络的模型的不确定性可以通过dropout算法进行计算。

网络训练过程中的目标函数为

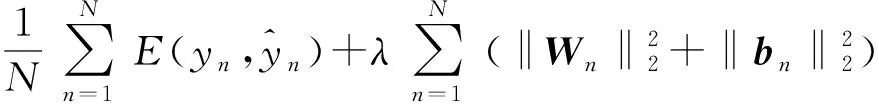
(9)

目标函数Ldropout可以通过常见的优化器(如随机梯度下降算法、Adam算法等)进行最小化，然后利用蒙特卡洛估计算法(也称为蒙特卡洛dropout算法)进行预测。对于新的输入样本x*，蒙特卡洛dropout算法通过V折交叉验证，可以得到预测结果的平均值和方差，模型为

(10)

2 复杂供输机构健康状态软测量方法

2.1 复杂供输机构健康状态软测量模型

复杂供输机构振动加速度信号中蕴含丰富的健康状态信息，但是其运行过程存在较大的冲击、振动，导致采集的监测信号具有噪声多、非线性、非平稳等特点，无法直接用于健康状态评估。小波分析构建时频图像数据能够有效反映振动信号中的瞬变特征。通过提取复杂供输机构不同循环周期时频图，记录机构不同运行阶段的健康状态。深度卷积网络能够有效提取图像特征，通过搭建不同的软测量模型分别实现复杂供输机构健康状态识别和性能退化程度定量评估。健康状态识别模型首先将试验数据分为正常运行阶段监测数据与性能退化阶段数据两类，利用深度卷积网络识别振动信号时频图特征，区分不同运行阶段；性能退化程度定量评估模型是将试验数据不同运行时刻的时频图作为输入数据，相应的运行时刻在整个运行周期中的百分比作为标签，利用深度卷积网络提取不同运行时刻的时频图特征，建立时频特征与运行时刻之间的映射关系。将测试数据时频图输入至已训练的网络，即可输出其对应运行时刻，进而实现健康状态评估。文献[20]表明，回归预测过程中，深度学习网络算法一个新点的输出应大致与最接近的训练点的输出相同。因此，模型输出结果即可认为是性能退化状态软测量值。在性能退化程度定量评估软测量模型中，采用dropout技术随机“丢弃”部分网络层之间的连接，减缓过拟合现象对评估结果的影响，导致软测量模型存在一定的不确定性，表现在评估结果中，即存在一定的置信区间。针对模型不确定性对软测量结果的影响，利用变分推断原理推导出软测量结果不确定的定量表达式，有效表示了模型不确定与最终评估结果之间的定量关系。

时频数据驱动的典型复杂供输机构软测量模型机构如图1所示，评估健康状态的步骤如下：

1)利用振动加速度传感器采集供输弹系统振动信号；

2)利用小波变换得到振动信号时频图；

3)将步骤2得到的时频图作为输入信号，分别输入到健康状态识别软测量模型和性能退化程度定量评估软测量模型，对模型进行训练；

4)将测试数据信号输入到构建好的模型中，得到供输弹系统健康状态软测量结果。

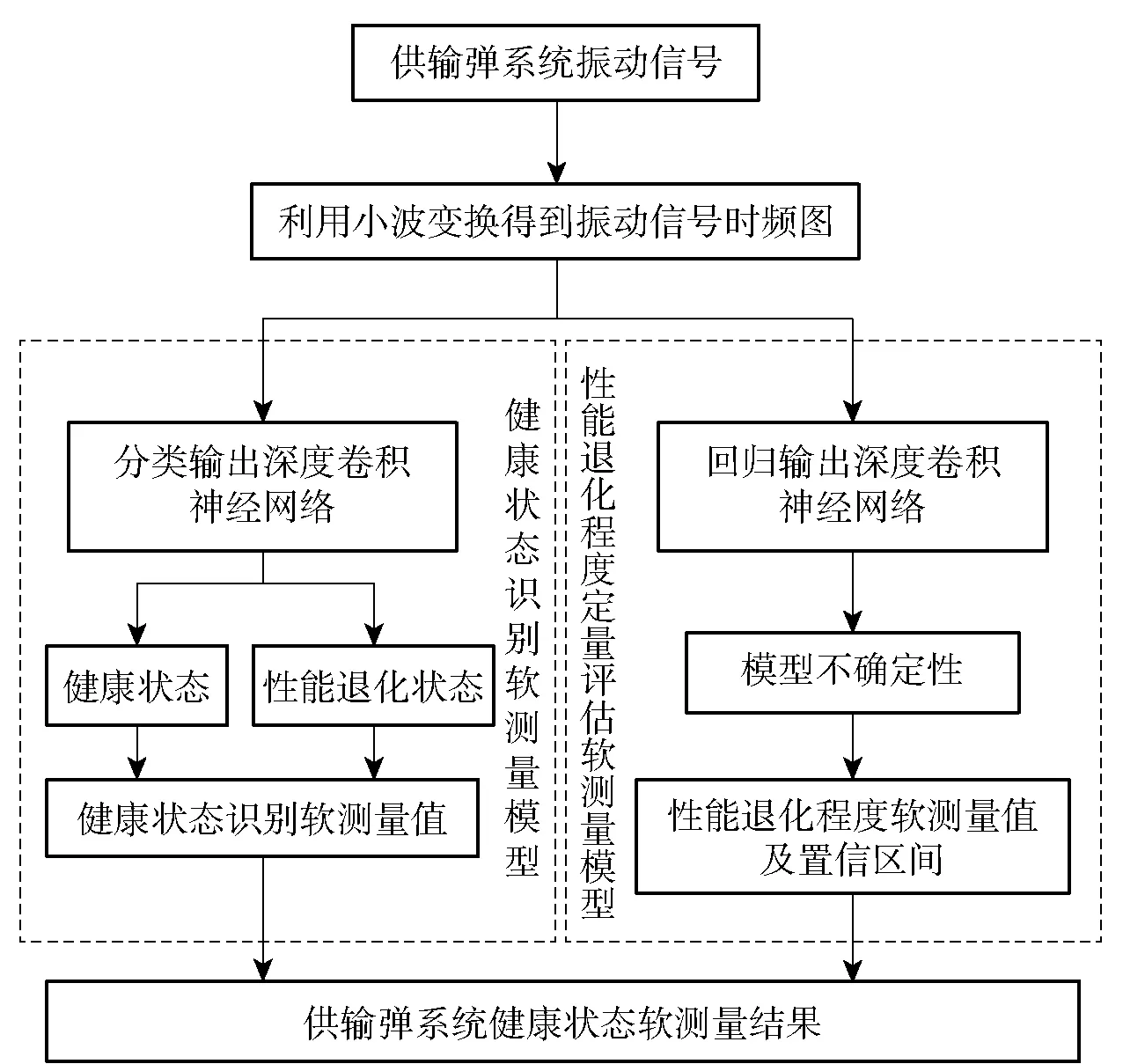
图1 复杂供输机构健康状态软测量模型Fig.1 Soft measurement model of complex feeding and ramming mechanism

2.2 基于多尺度卷积网络的图像特征提取

深度卷积网络通常将最后一层池化层提取的特征输入至全连接层进行回归预测，该全局特征比上一层卷积层提取的特征更加稳定。但是，卷积层提取的特征经过池化层后，会丢失一些局部特征，导致特征提取不充分。针对该问题，本文提出一种多尺度深度卷积神经网络结构，如图2所示。多尺度卷积网络是在卷积网络结构基础上，将最后一层池化层与上一层卷积层展平后相连接，组成一个特征向量，输入到全连接层进行回归预测。

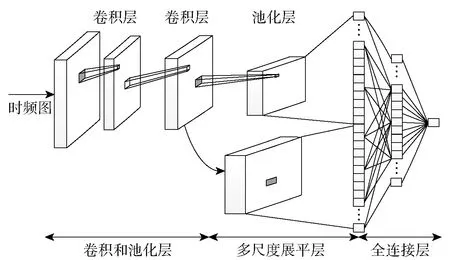
图2 多尺度卷积网络结构图Fig.2 Structure of multi-scale convolutional network

卷积网络展平层的输出为

(11)

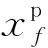
经过改进后的卷积网络，其多尺度展平层的输出为

(12)

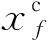
对比(11)式、(12)式可知，多尺度卷积网络的多尺度展平层同时包含了池化层与卷积层提取的特征，增强了网络特征提取能力，有利于反映滚动轴承早期性能退化状态。

2.3 考虑模型不确定性的性能退化状态定量评估

考虑深度学习模型不确定性的性能退化状态定量评估方法流程如图3所示。

3 供输机构台架试验验证

3.1 台架试验设计

某型复杂供输机构试验台架如图4所示。该试验台架包含动力装置、试验台架体、控制装置及摆动机构组成。试验平台采用移动式液压站为动力，通过外能给复进机储能并保持，在人工后坐油缸返回到位后，扳机释放尾部铁块，尾部铁块在复进过程中为摆弹机储能。

图4 复杂供输机构试验台架Fig.4 Test rig for complex feeding and ramming mechanism

尾部铁块在滚轮带动下向后移动，摆动机构带动摆臂由竖直方向摆动90°，使摆臂与地面平行。滚轮健康状态好坏将直接影响尾部铁块运行能否到位，进而影响摆臂能否正常摆动到位。由于滚轮在每次摆臂过程中受到一定的载重力，且反复运用，磨损较大，其健康状态将直接影响复杂供输机构能否正常运行，一定程度上反映了复杂供输机构的健康状态。由于滚轮位于凹槽内，位置隐蔽，空间狭小，无法直接安装传感器(见图5)。而摆动机滑板、压板机在滚轮运动过程中处于滚轮正上方且距离滚轮较近，便于布置传感器，因此在摆动机滑板、压板机附近布置6个振动加速度传感器，分别为测点1～测点6，如图6所示。

图5 供输机构滚轮及滑槽Fig.5 Roller and spout for feeding and ramming mechanism

图6 传感器布置Fig.6 Sensor layout

传感器类型为压电集成电路加速度传感器，采样频率为10 kHz，采用德国西门子公司生产的32通道LMS信号采集系统。本文试验分为2组：第1组采用健康状态的滚轮循环运行11组、每组循环包括20次动作；第2组换装性能退化阶段的滚轮循环运行9组，每组循环包括20次动作。

试验后期，滚轮出现较大裂纹，为安全起见，停止试验，认为滚轮已经达到寿命阈值。性能退化阶段的滚轮和试验后出现较大裂纹的滚轮如图7所示。

图7 性能退化阶段及出现较大裂纹的滚轮Fig.7 Performance degradation stage and large cracks in the roller

3.2 台架试验数据采集

选取位于滚轮正上方测点1处的振动传感器数据进行分析。健康状态和性能退化状态下测得的振动加速度信号分别如图8(a)和图8(b)所示。由图8可知，供输系统测得的振动加速度信号中有较大的冲击振动。同时，仅从原始振动加速度信号来看，无法有效区分健康状态和性能退化阶段。

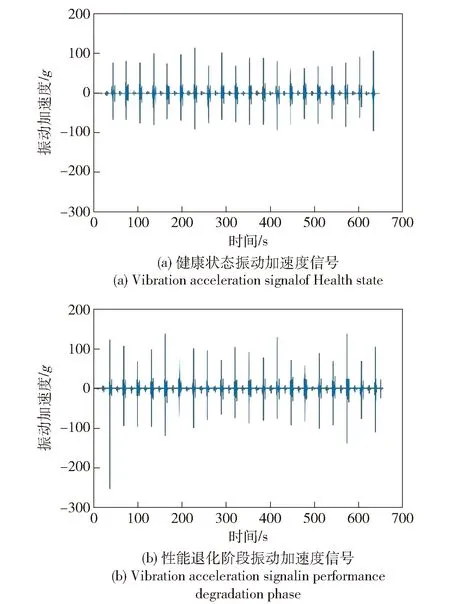
图8 原始振动加速度信号Fig.8 Original vibration acceleration signal

供输系统试验平台采用自动控制系统控制每个动作的运行时间，一个循环周期的时间大约为31.2 s。提取其中一个运行周期的振动加速度信号，如图9所示。该循环过程主要包括4个运动过程：摆动机构储能、扳机解脱、拉钩解脱、摆动到位。通过图9可知，该循环过程的振动加速度信号属于非平稳信号，频谱分析难以得到系统性能退化的特征。

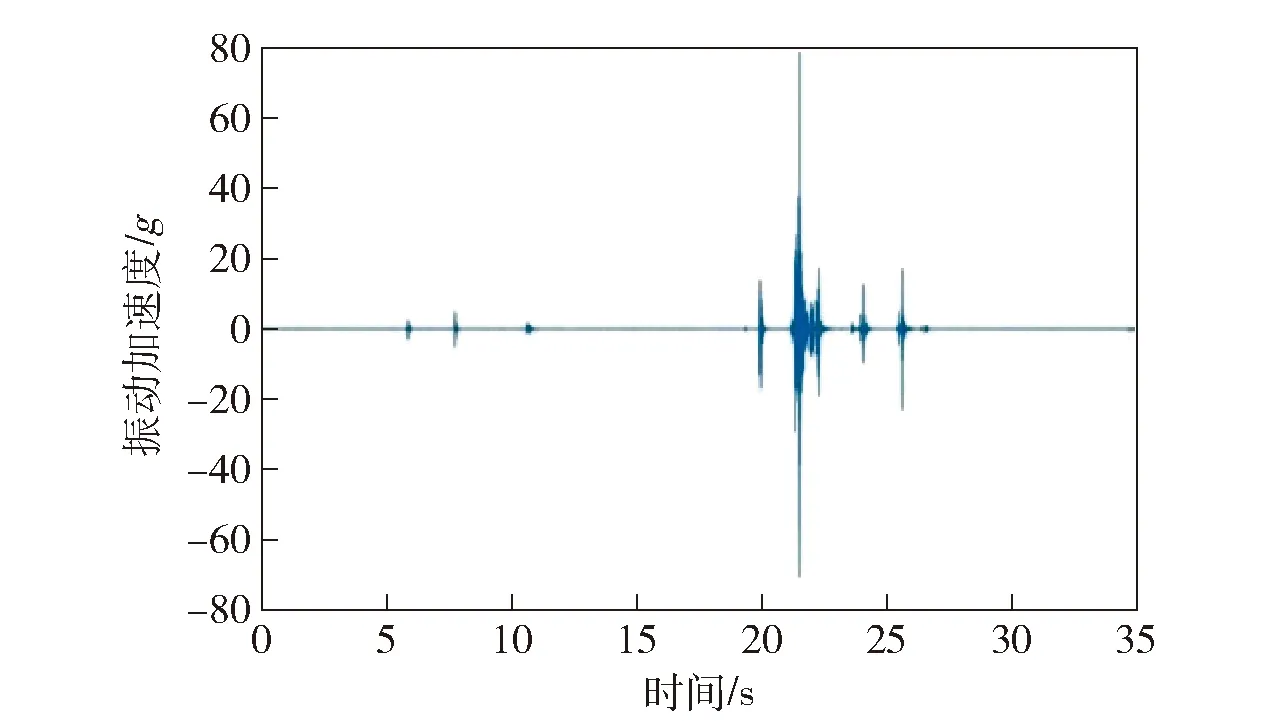
图9 一个循环的振动加速度信号Fig.9 A cyclic vibration acceleration signal

基于(1)式可得，供输系统健康状态和性能退化状态的时频图如图10所示。

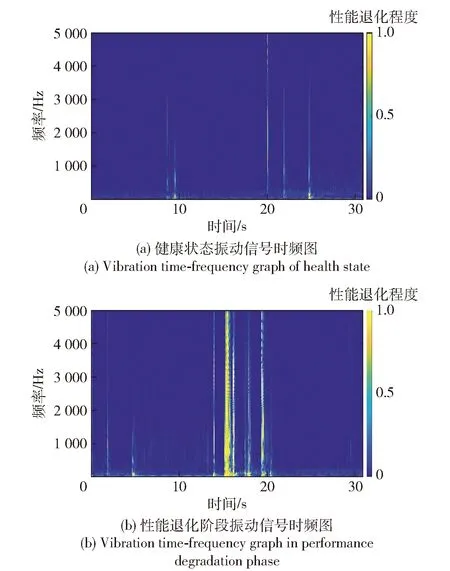
图10 一个循环的时频图Fig.10 Time-frequency map of a cycle

观察图10可知，供输系统振动信号的能量几乎分布在所有频段，且中低频段内的能量高于高频段内的能量。在一个循环周期内，出现明显的能量波动，信号的瞬变特征明显。对比健康状态和性能退化阶段的时频图可知，性能退化阶段的信号能量高于健康状态的信号能量，同时二者瞬变过程也存在差异。

提取性能退化阶段不同时期的时频图，如图11所示。由图11可知，性能退化阶段的时频图变化并不明显，无法直接判断性能退化程度。因此，需要通过卷积网络提取深层特征，定量表征性能退化程度。

图11 性能退化阶段不同时期的时频图Fig.11 Time-frequency maps of different degradation periods

健康状态和性能退化阶段的振动信号时频图共400组数据，将其随机打乱后选择其中的300组数据作为训练数据，100组数据作为测试数据。

3.3 试验结果及分析

由于学习过程中，网络结构的增加、学习率的大小、卷积核宽度的增减、Dropout值的高低均可能造成模型过拟合。目前，还没有统一的确定超参数的理论。本文综合考虑试验数据量大小，输入的时频图大小，采用手动调整超参数的方法，确定使得验证误差相对较小的超参数值，如表1所示。

表1 网络超参数

为了进一步分析不同网络层学习得到的特征，将测试集中的时频图输入到已训练的网络中，分别提取第1层和第2层卷积层学习到的图像特征，如图12所示。

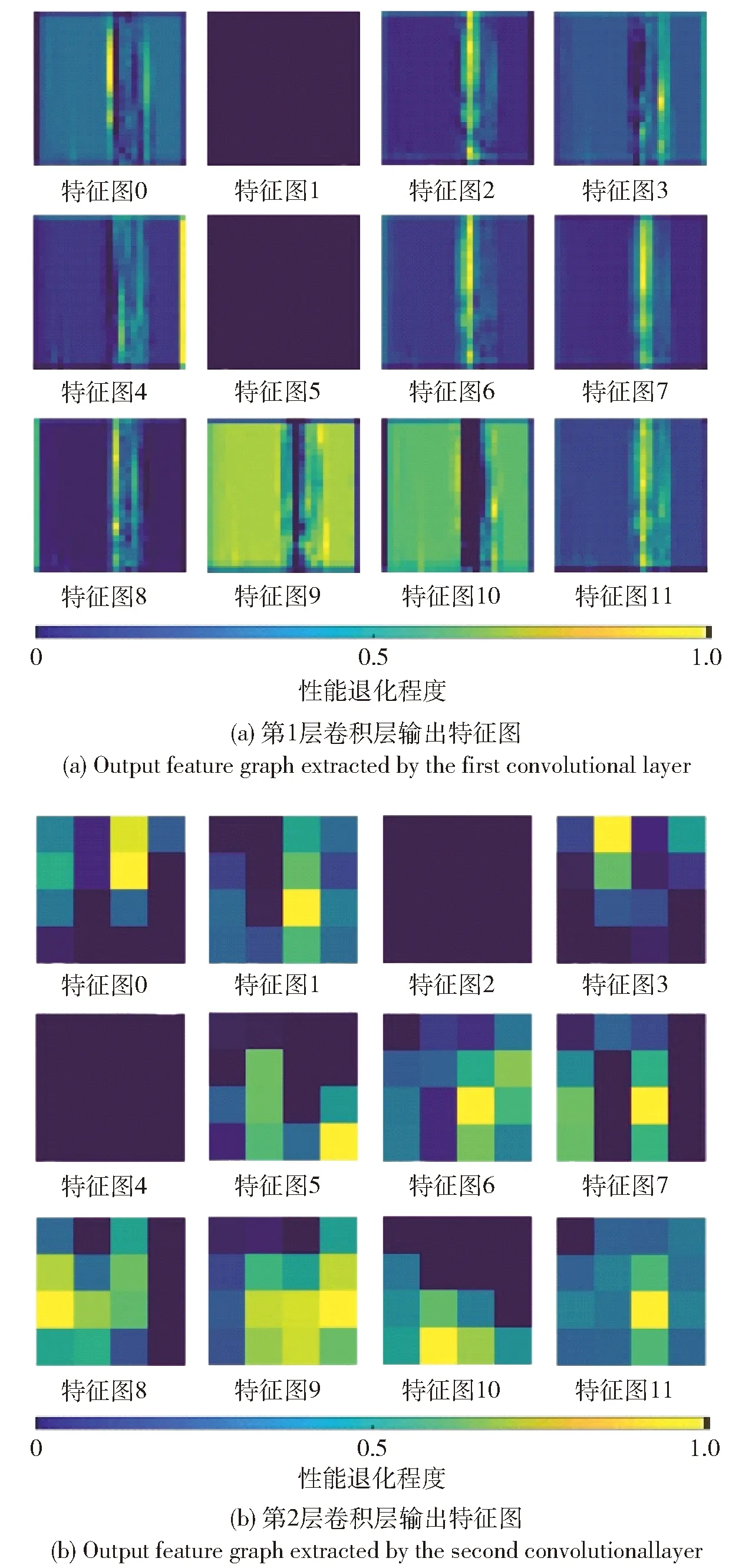
图12 不同卷积层提取的特征图Fig.12 Feature graphs extracted by different convolutional layers

由图12可知，随着卷积层数的增加，网络提取的特征愈加抽象。由第1层卷积层提取的特征图2、特征图6、特征图7、特征图9、特征图10、特征图11可知，性能退化阶段的特征大约出现在一个循环的22 s附近，此时供输系统进行摆弹动作，性能退化的滚轮在凹槽内滑动，与实际情况相符合，说明网络学习到了性能退化阶段滚轮运行的时间特征；通过第2层卷积层输出的12个特征图可知，能量较高的模块大都集中在中低频段，可知表征滚轮性能退化阶段的频率也大都集中在中低频段。由此可见，网络能够有效学习供输系统健康状态与性能退化阶段的频谱特征。

为了验证本文所提方法的有效性，与两种常用的识别方法进行对比。识别准确率曲线如图13所示。第1类信息熵结合神经网络的识别方法是指提取振动信号时域信息熵作为输入，搭建基于神经网络的软测量模型，输出健康状态识别结果(简称信息熵+神经网络方法)。第2类方法是提取振动信号时域均方根(RMS)作为输入，搭建基于神经网络的软测量模型，输出健康状态识别结果(简称RMS+神经网络方法)。由图13可知，本文所提方法在迭代训练80次后识别准确率可达90%，信息熵+神经网络方法在迭代训练50次后，识别准确率基本稳定在70%，RMS+神经网络方法识别准确率较低，仅有55%。

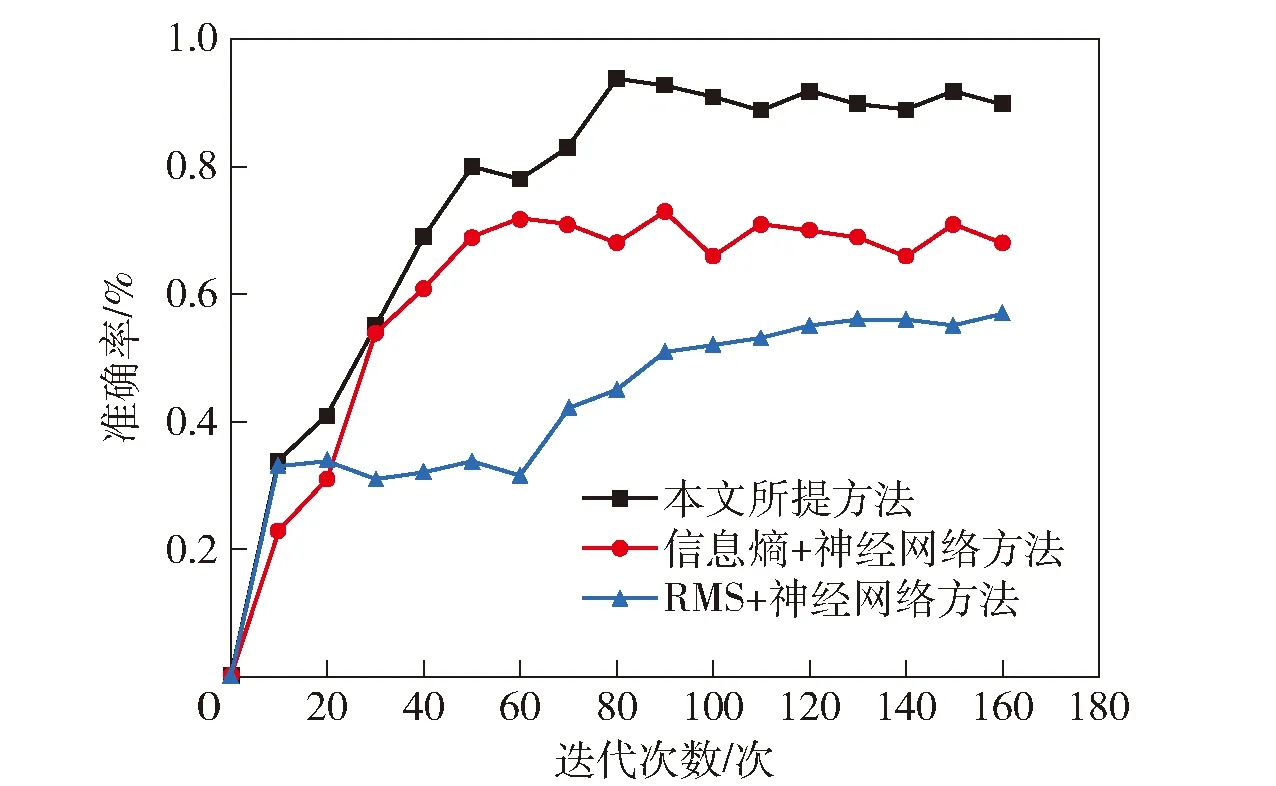
图13 不同方法的识别准确率Fig.13 Recognition accuracies of different methods

当供输系统进入性能退化阶段时，本文提出一种基于深度卷积神经网络的回归预测模型，能够定量测量性能退化状态，进而为下一步的剩余寿命预测奠定基础。本文搭建的用于回归预测的深度卷积神经网络是在分类深度卷积神经网络的基础上，将最后的二分类层改为回归预测层，输出节点数为1。供输系统进入性能退化阶段后是一个循序渐进的过程，即从性能退化开始一直到滚轮出现裂纹无法工作的过程是单调不可逆的。将供输系统性能退化阶段采集到的振动加速度信号转换成时频图后作为深度卷积神经网络的输入，可表示为It={xt,yt}，其中：xt为t时刻一个循环内尺寸为H×H的时频图，xt∈RN×N，H为整数，表示时频的尺寸，本文采用的时频图尺寸为100×100；yt为t时刻循环对应的供输系统性能退化程度，yt∈[0,1]，yt=t/T，T表示总的运行时间。通过多次试验可知训练数据标签yt与循环时刻t的关系并不影响最终的健康因子构建结果。因此，在此选择线性模型构造训练数据标签。此处，供输系统共运行了400个循环，则第200个循环对应的退化程度yt=200/400=0.5。将所有数据随机打乱后分为训练组与测试组，利用训练集对深度卷积网络进行训练，将测试数据输入到已训练的深度卷积网络，得到性能退化定量测量结果。将所有数据输入到训练好的网络中，得到供输系统性能退化曲线，如图14所示。由图14可知，网络能够根据设定标签有效学习到滚轮性能退化过程。将测试数据输入到训练好的网络中，得到性能退化程度预测值。

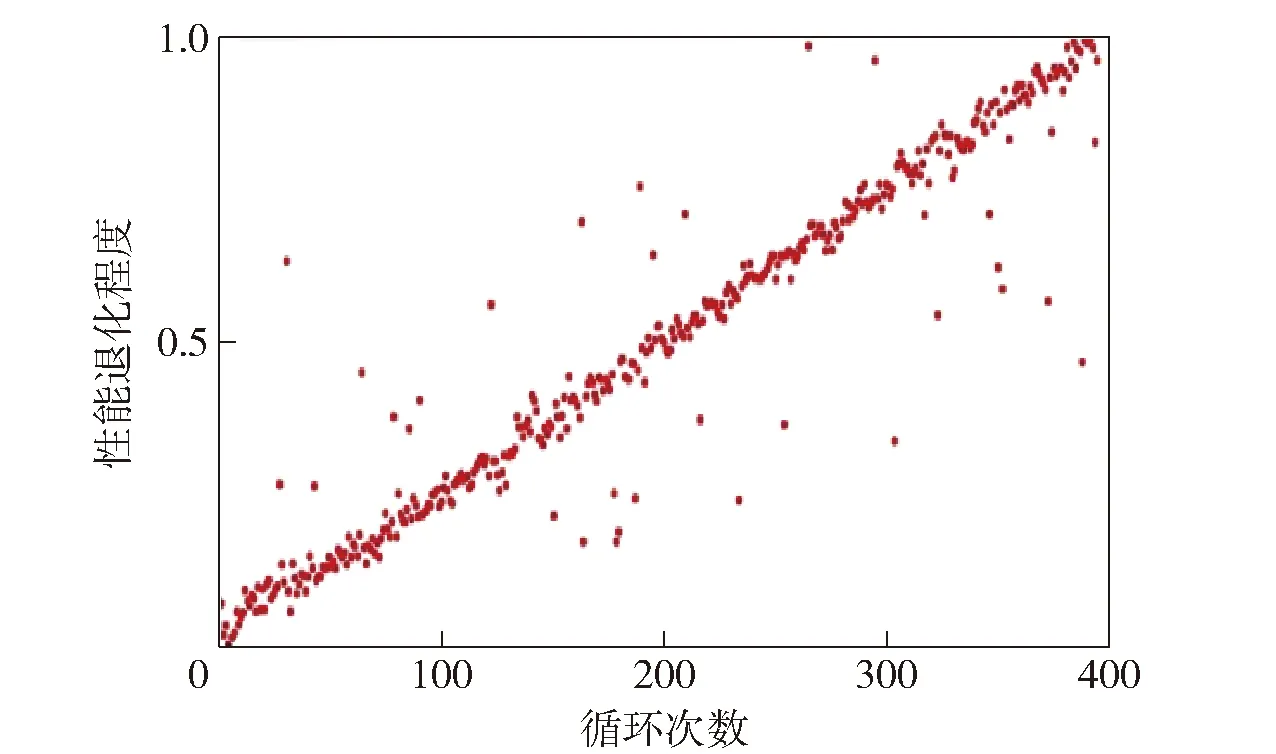
图14 供输系统性能退化曲线Fig.14 Performance degradation curve of feeding and ramming mechanism

利用预测结果与真实结果的相对误差作为评估预测精度的准则，计算公式为

(13)

式中：Erη表示第η次循环得到的预测精度值；ActDgredη表示第η次循环实际的性能退化程度；Dgredη表示第η次循环软测量模型预测的性能退化程度。

将本文所提方法的软测量精度与其他3类方法进行对比分析，结果如图15所示。RMS+神经网络方法表示提取RMS作为特征，利用神经网络预测性能退化程度；信息熵+神经网络方法表示提取信息熵作为特征，利用神经网络预测性能退化程度；时频图+神经网络方法表示提取时频图作为特征，利用神经网络预测性能退化程度。时频图+神经网络方法来自文献[21]，其卷积网络结与本文方法不同，没有设置dropout层。由图15可知，本文方法的相对误差最小，即测量精度最高。同时，测量结果误差范围相对较小，表明该方法具有一定的稳定性。对比时频图+神经网络方法可知，没有采用dropout层的卷积网络测量精度与本文所提方法接近，但是测量结果误差范围较大，同时，出现两个异常点，可能的原因是网络出现一定程度的过拟合。

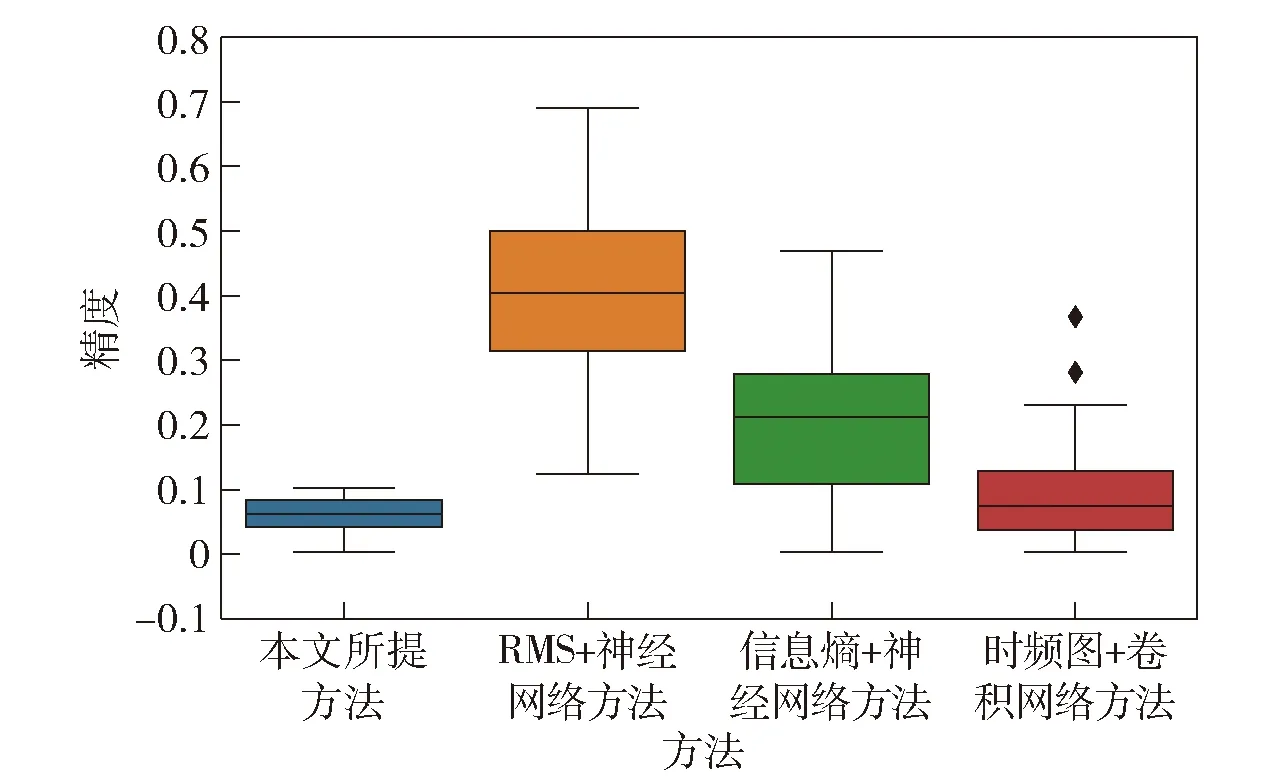
图15 不同方法的精度对比图Fig.15 Accuracy comparison of different soft measurement methods

为了验证dropout正则化项是否能够缓解过拟合现象，将实验数据随机分为两组，其中350组数据作为训练集，50组数据作为验证集，将dropout值分别设为0.1、0.2、0.3、0.4，计算训练集、验证集的损失函数值，结果如表2所示，当dropout取值为0时，训练集损失函数值最小，拟合度最高，但是在验证集上的损失函数值最大，说明过拟合现象最严重；随着dropout值的增加，训练集上的损失函数值先增加、后平稳变化，而验证集上的损失函数值则先减小、后增加。训练集和测试集损失函数差值先减小、后增加。当dropout值为0.2时，其在验证集上的损失函数值最小，且训练集与验证集损失函数差值最小，说明添加dropout正则化项后一定程度上缓解了过拟合问题，且不同dropout值对过拟合问题的缓解程度存在差异。

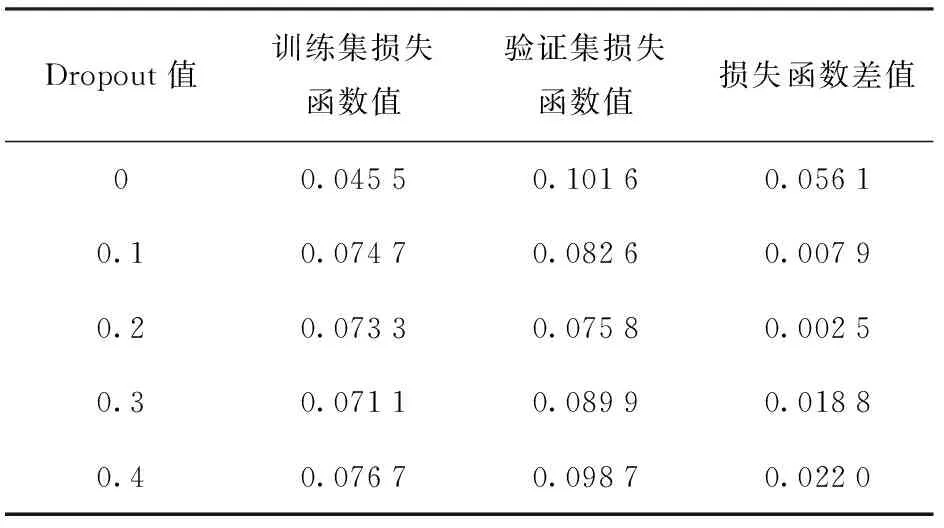
表2 不同dropout值下的损失函数值

为了进一步评估不同dropout取值对模型不确定性的影响，以第49个测试数据为例，dropout取值分别为0.1、0.2、0.3、0.4时的概率分布如表3和图16所示。图16中，4组曲线对应的均值分别为0.602、0.610、0.511、0.562，这4组值是将第49个测试数据的时频图输入到训练好的模型中，模型对应的输出值，即为软测量结果。总的试验循环次数为400次，因此对应的软测量循环次数依次240.8、244.0、224.8、204.4，实际的循环次数应为245.2。由于循环次数应为整数，四舍五入后的软测量结果分别为241、244、224、204。将软测量结果代入(13)式中，即可计算得到对应的软测量精度分别为1.63%、0.41%、8.57%、16.73%。由此可知，随着dropout的取值增加，软测量精度先是逐渐增加，之后逐渐减小。当dropout值由0.1变为0.2时，软测量精度增加，同时数据分布方差变小，即模型不确定性降低。以上结果表明，当dropout值为0.2时，模型容量与数据最匹配，得到的软测量精度最高，模型不确定性相对较小。由表3和图16可知，随着dropout值的增加，模型不确定性不断增大，测量结果的方差增加，即结果不确定性增加。

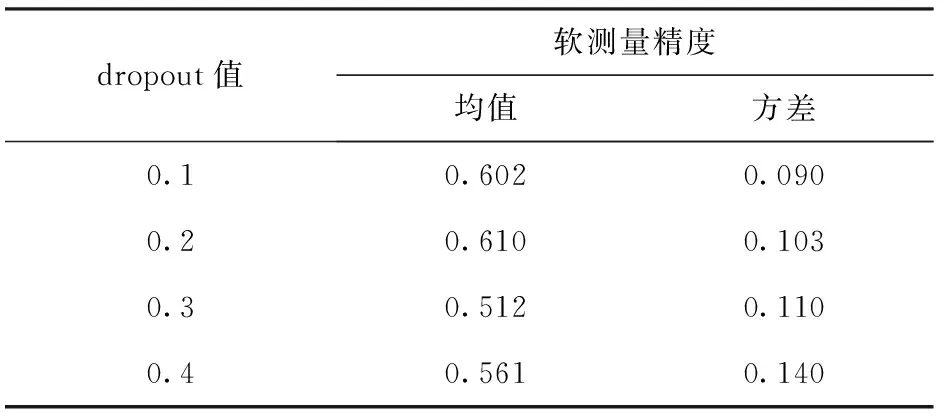
表3 不同dropout值的测量结果

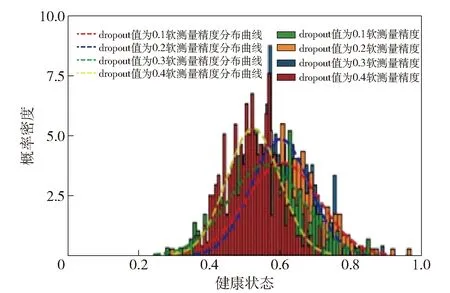
图16 软测量结果概率密度曲线Fig.16 Probability density curve of soft measured results

4 结论

为解决复杂力学环境下工作的供输机构健康状态评估问题，本文提出了一种基于时频图和深度卷积网络的健康状态软测量方法。通过morlet小波变换提取振动信号时频图作为输入特征，构建了基于深度卷积网络的软测量模型，并引入dropout正则化层，实现了供输机构健康状态识别和性能退化程度定量评估。利用典型供输机构台架试验验证了所提方法的有效性，与不同方法的对比分析表明，基于时频图和深度卷积网络的软测量方法能够有效提高供输机构健康状态识别准确率和性能退化程度软测量精度，降低测量结果的不确定性。本文研究方法对复杂供输机构健康状态评估提供了一种新的思路，也为供输机构健康管理提供一定的理论参考。