四旋翼飞行器的固定时间轨迹跟踪控制

王 宏，刘宜成，涂海燕，熊宇航，陈 杰

(四川大学电气工程学院，成都 610000)

0 引言

近年来，四旋翼飞行器凭借其小巧灵活、机动性强、造价低廉等诸多优点，备受青睐而广泛用于军用、民用领域，受到国内外各界的密切关注[1]。四旋翼飞行器系统是一种多输入多输出的复杂非线性欠驱动系统，具有强耦合的特点，在飞行控制方面较为困难。因此，对四旋翼飞行器控制方法进行研究具有理论意义和应用价值。

为了提高四旋翼飞行器的轨迹跟踪性能，国内外众多研究人员针对位置和姿态控制问题，提出了许多控制方法，较典型的有PID控制、反演控制[2]、滑模控制[3]等。文献[4]提出一种基于有限时间收敛干扰观测器的分层控制器，利用该观测器在线估计未知的不确定性和扰动。然而，有限时间控制的收敛时间通常与系统的初始状态有关，初始状态偏离平衡点较远会导致收敛时间过长，为了解决该问题，文献[5]首次提出了固定时间稳定理论，并给出了固定时间稳定的定义，保证收敛时间具有明确上界，摆脱了对初始状态的依赖。之后，固定时间理论迅速成为研究热点，文献[6]针对柔性吸气式高超声速飞行器，提出一种基于固定时间扰动观测器的固定时间反演控制算法，采用一种与初始状态无关的固定时间扰动观测器来估计和补偿跟踪过程中的不确定性。

本文针对四旋翼飞行器系统，基于反演法提出一种保证系统全局固定时间稳定收敛的新型控制方法。使用固定时间干扰观测器对四旋翼飞行器所受外界扰动与自身建模不确定性组成的混合扰动进行估计，通过固定时间命令滤波器对虚拟信号进行处理来避免因多次求导而引起的“微分爆炸”问题，相比于传统命令滤波器[7]，可使滤波器的输出更加接近于虚拟控制信号的导数。建立一种新的误差补偿系统来减小微分器带来的影响，保证四旋翼系统的跟踪误差可以在固定时间内收敛到平衡点附近的一个小邻域内，且收敛时间上界与系统初始状态无关，同时使得闭环系统的所有信号都是有界的。最后，通过仿真验证了本文方法的有效性和优越性。

1 四旋翼飞行器模型描述和预备知识

1.1 四旋翼飞行器模型

四旋翼飞行器是具有六自由度的单刚体结构，如图1所示，要准确地描述四旋翼飞行器的空间运动状态，需按不同坐标原点位置建立惯性坐标系E(xe,ye,ze)和机体坐标系B(xb,yb,zb)，f1～f4表示4个旋翼产生的升力。

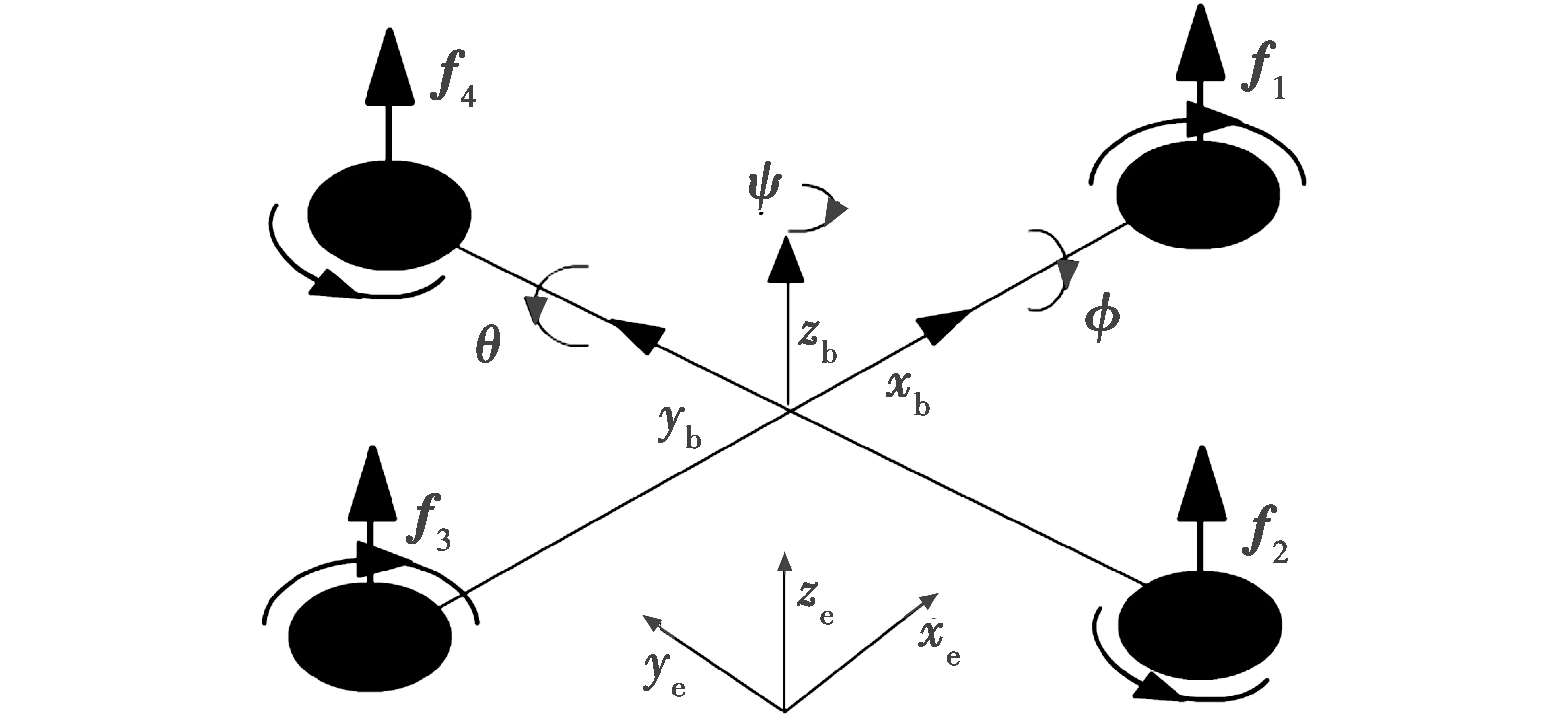
图1 四旋翼飞行器结构图Fig.1 Structure diagram of quadrotor aircraft

根据四旋翼飞行器飞行原理可知，其所有运动方式都直接由4个旋翼的转速决定，而转速的快慢则由控制输入的大小决定。因此，为了便于理解与设计控制器，结合旋翼动力学，四旋翼飞行器线速度的控制输入定义为U1，横滚角、俯仰角和偏航角的控制输入定义为τ=[τ1τ2τ3]，各控制输入量与各桨叶转速的关系为

(1)

(2)

其中：Ωi(i=1,2,3,4)为旋翼的转速；kf和kN分别为旋翼升力系数和扭力系数的简化值；l为各电机中心与质心的距离。

四旋翼飞行器位置子系统的状态空间描述可写为

(3)

其中：[xyz]T，[vxvyvz]T，分别为四旋翼飞行器在惯性系下的位置向量和线速度向量，分别记为ξ和v;U1表示线速度的控制输入；[d1xd1yd1z]T为由风力、空气阻力等外部干扰和系统自身建模不确定性组成的混合扰动，记为d1；m为机体质量；g为重力加速度。

四旋翼飞行器姿态角子系统的数学模型可写为

(4)

式中：η=[φθψ]T，为欧拉角向量，φ,θ,ψ分别表示横滚角、俯仰角和偏航角;w=[pqr]T，为角速率向量，且四旋翼飞行器角速率子系统的状态空间描述可写为

(5)

式中：d2=[d2φd2θd2ψ]T,表示风力、空气阻力等外部干扰和系统自身建模不确定性组成的混合扰动；M=[qr(Jy-Jz)/Jxpr(Jz-Jx)/Jypq(Jx-Jy)/Jz],Jx，Jy，Jz分别为绕机体xb，yb，zb轴的转动惯量;N=diag(1/Jx,1/Jy,1/Jz)。

做如下一般性假设。

假设1 期望轨迹[xdydzd]T和ψd连续有界，其一阶导数存在且有界。

假设2 风力、空气阻力等外部干扰和系统自身建模不确定性组成的混合扰动di有界且受限于已知充分光滑非线性函数Γi，即||

di||

≤Γi,i=1,2。

1.2 预备知识

考虑如下自治非线性系统

(6)

式中：x(t)∈Rn，是系统的状态变量；f(x(t))∈R+×Rn,表示光滑的非线性函数。

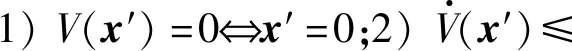
(7)

(8)

式中，常数ρ∈(0,1)。收敛到残差集内的时间满足

(9)

引理3[8]对于xi∈R,i=1,2,3,…,n,λ∈(0,1]，如下关系成立

(10)

引理4[9]杨不等式方程

(11)

式中,a,b大于0，ε为任意正整数，当且仅当ab=ε时等号成立。

2 控制器设计

2.1 固定时间干扰观测器

根据所建数学模型，四旋翼飞行器在平移运动过程中受到的混合扰动可以记为d1，旋转运动过程中所受的混合扰动可以记为d2。

针对扰动d1设计固定时间干扰观测器如下

(12)

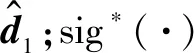
(13)

针对扰动d2设计固定时间干扰观测器如下

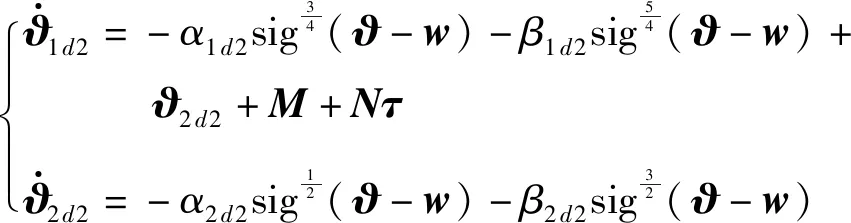
(14)

(15)

2.2 固定时间命令滤波器

本文使用固定时间滤波器[11-12]，可以使滤波跟踪误差在固定时间内收敛到平衡点附近一个极小的闭球区间内，滤波器形式如下

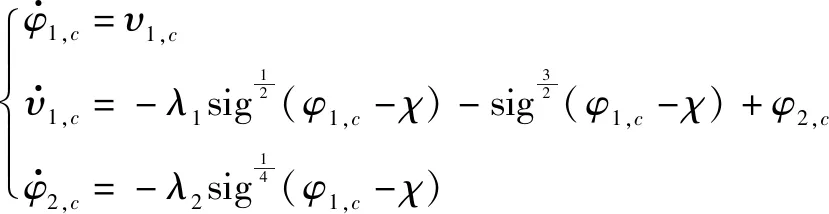
(16)

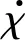
2.3 位置子系统控制器设计

为了简化控制器的设计，根据位置子系统的状态空间描述式(3)，可以定义虚拟控制输入为

(17)

式中，ux，uy，uz分别是x，y，z方向上的虚拟控制输入，记为u。则平移运动学方程可以写为

(18)

(19)

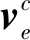
(20)

对位置误差设计虚拟控制律ve，对线速度误差设计控制输入u，分别为

(21)

式中：ki=diag(kix,kiy,kiz),si=diag(six,siy,siz)，i=1,2，均为大于0的常参数；e1,e2为补偿后的跟踪误差；γ为常参数且满足0<γ<1。因为使用命令滤波器会产生滤波误差，影响系统性能，本文引入误差补偿机制，e1,e2分别定义为

(22)

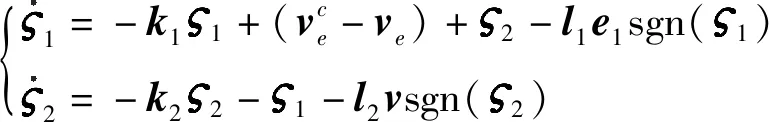
(23)

式中，参数li=diag(lix,liy,liz)>0,i=1,2。

在进行姿态控制器之前，需获取机体的期望姿态信息ηd，由虚拟控制输入ux，uy，uz可以反解得到位置子系统的速度控制输入U1为

(24)

期望偏航角ψd为给定条件，由U1可解得期望横滚角φd和期望俯仰角θd分别为

(25)

2.4 姿态子系统控制器设计

欧拉角和角速率的误差定义为

(26)

(27)

式中：ki=diag(kiφ,kiθ,kiψ)，si=diag(siφ,siθ,siψ)，为大于0的设计参数,i=3,4；e3,e4是命令滤波误差信号补偿后的跟踪误差，分别定义为

(28)

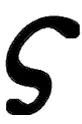
(29)

式中，li=diag(liφ,liθ,liψ),为大于0的待设计常参数，i=3,4。

3 稳定性分析

总结以上设计，建立补偿后的整个跟踪误差子系统为

(30)

考虑误差e1设计候补李雅普诺夫函数V1为

(31)

对式(31)求导得

(32)

考虑误差e2设计修正后的候补李雅普诺夫函数V2为

(33)

对式(33)求导得

(34)

(35)

对式(35)求导得

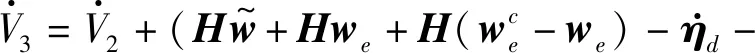
(36)

考虑误差e4设计候补李雅普诺夫函数V4为

(37)

对式(37)求导得

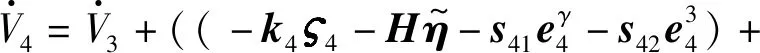
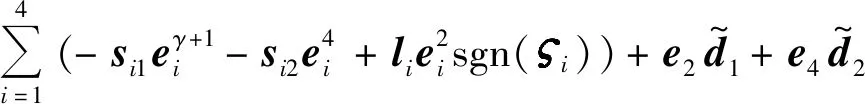
(38)

根据引理4可得

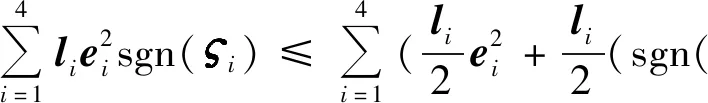
(39)

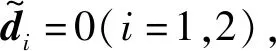
(40)

4 数值仿真

为了验证本文方法的有效性，在Matlab中针对四旋翼飞行器模型进行了仿真，四旋翼的主要参数见表1。

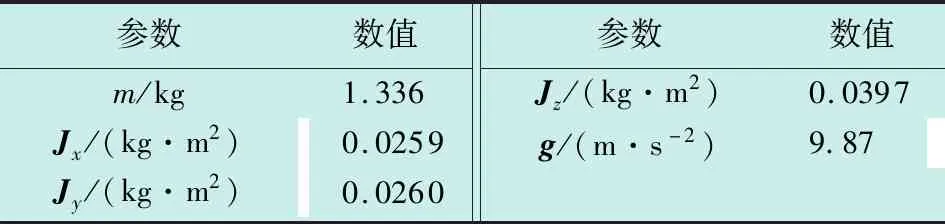
表1 四旋翼飞行器模型参数Table 1 Parameters of quadrotor aircraft model

固定时间滤波器的参数选择为λ1=19,λ2=2，控制器参数选择:ki=diag(12,12,12),i=1,2，k3=diag(7.5,7.5,7.5),k4=diag(18,18,18),si1=diag(10,10,10),i=1,2，si2=diag(20,20,20),i=1,2，si1=diag(5,5,5),i=3,4,si2=diag(8,8,8),i=3,4，li=diag(2,2,2),i=1,2,3,4。

在上述初始条件和模型参数等条件下，将本文方法与文献[13]所提出的有限时间干扰观测器方法进行对比仿真。仿真结果如图2～5所示。

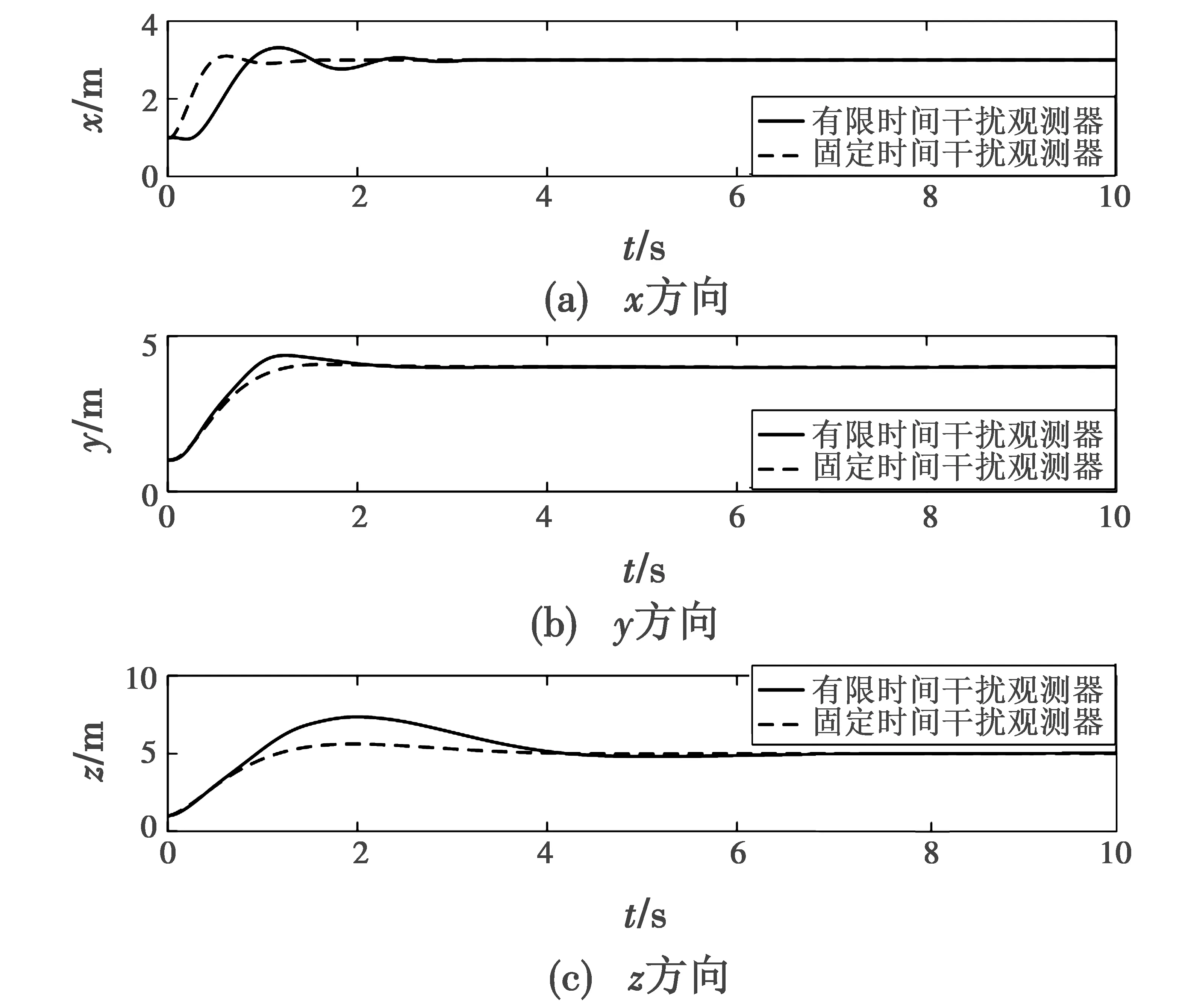
图2 位置响应曲线对比Fig.2 Comparison of position response curves

从图2来看，本文所设计的控制器在x,y,z方向上分别于1.8 s,2 s,3.8 s左右实现稳定跟踪且跟踪误差收敛到零的附近，而文献[13]所提方法则分别于3.2 s,3 s,4.5 s左右实现稳定收敛。从图3来看，本文方法的收敛精度高于有限时间干扰观测器方法的精度。从图4和图5来看，本文方法在姿态控制上比文献[13]所提方法的收敛速度更快。以上仿真结果表明本文设计方法在系统跟踪控制上的有效性和优越性。

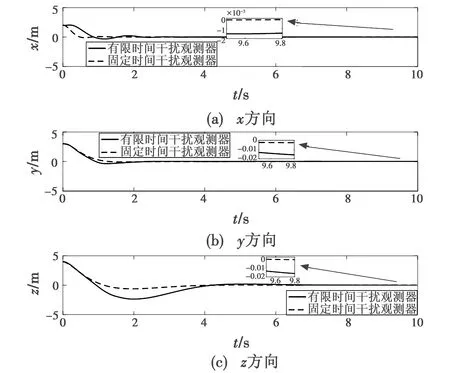
图3 位置误差曲线对比Fig.3 Comparison of position error curves

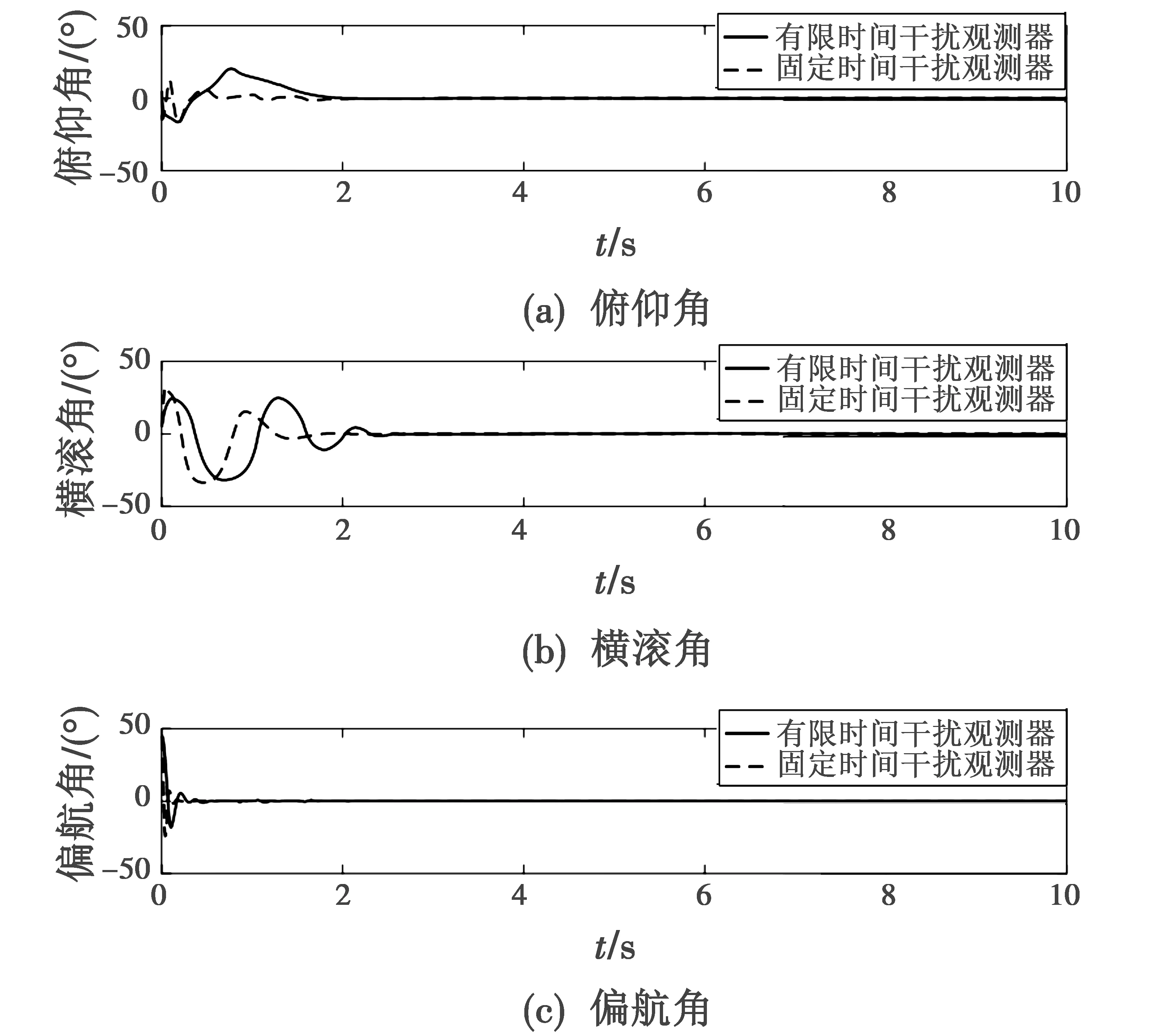
图4 姿态响应曲线对比Fig.4 Comparison of attitude response curves

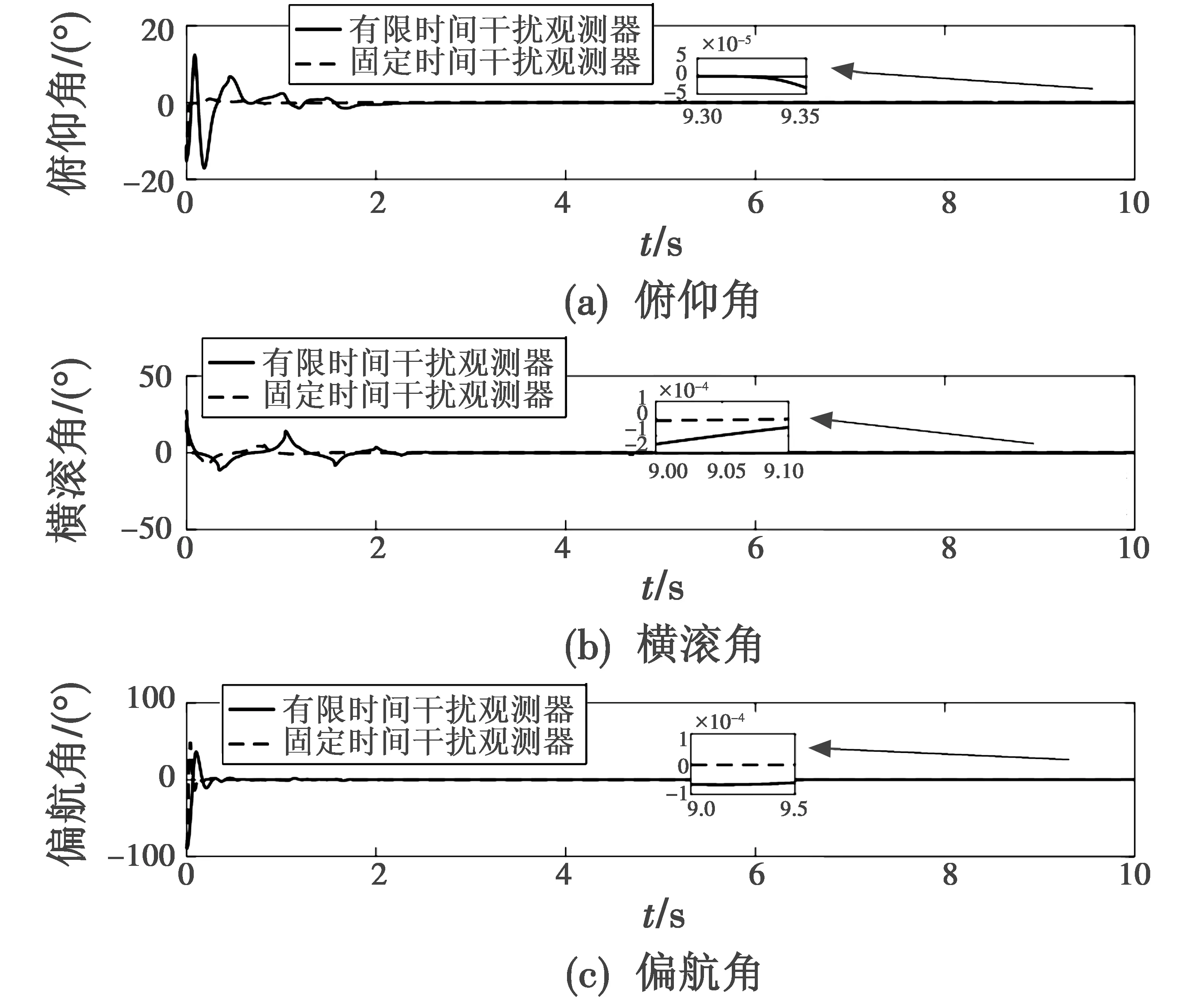
图5 姿态误差曲线对比Fig.5 Comparison of attitude error curves

5 结论

针对四旋翼飞行器轨迹跟踪稳定问题，本文提出一种基于固定时间干扰观测器的固定时间反演控制算法。将四旋翼飞行器分为位置和姿态两个子系统分别进行控制，降低了耦合性与设计难度。使用固定时间干扰观测器对四旋翼飞行器受到的内外部混合扰动进行估计，以此来抑制干扰。采用固定时间命令滤波器对虚拟控制信号进行处理，有效地解决了传统反演法中的“微分爆炸”问题，并建立误差补偿系统对滤波误差进行补偿，提高系统的动态性能。利用Lyapunov稳定性理论证明系统可以在固定时间内收敛到平衡点附近的一个非常小的闭球区间内。最后，通过仿真验证了本文设计方法的有效性和优越性。