基于响应面法的重载机械臂优化设计

徐赛华，张高峰，杨秀萍，王收军

（1.天津理工大学机械工程学院 机电工程国家级实验教学示范中心，天津 300384；2.天津理工大学 天津市先进机电系统设计与智能控制重点实验室，天津 300384；3.南京晨光集团有限责任公司，南京 210006）

0 引言

重载机械臂广泛用于矿山、冶金和航天航空等工业领域，是实现灵巧工作和安全生产、降低人力成本、提高工业效率的重要工作装置。在工作过程中，在保证机械臂安全准确工作的同时，应尽可能减轻其自重，因此，对机械臂结构进行优化设计十分必要[1，2]。

近年来，对于大型机械装备，研究人员采用了不同方法进行设计及优化。陈继文等[3]对码垛机器人小臂进行拓扑优化，实现轻量化；李伟等[4]应用响应面优化法对变速箱壳体进行设计；刘明亮等[5]对极限工况下的安全阀自动上料机械手抓取机构进行应力分析，采用MOGA算法对其变量优化以减小总质量；王小明等[6]采用响应面分析法中的中心组合设计对货叉进行尺寸优化。

本文采用ANSYS Workbench软件对重载机械臂的三种工况进行静力学分析，得到相应的应力和变形云图；根据Box-Behnken试验设计方法对伸缩臂的截面尺寸进行设计，采用响应面法，得到伸缩臂最优设计参数组合；在ADAMS中利用刚柔耦合仿真分析对比优化前后重载机械臂的轨迹总误差，验证了优化结果的可行性。

1 重载机械臂有限元分析

1.1 有限元模型

重载机械主要由抓手、仰俯摆动马达、滚摆马达、进退导轴、平摆马达、伸缩内臂、伸缩外臂、变幅缸和回转驱动组成，如图1所示。在SolidWorks中建立重载机械臂的几何模型，将其导入到ANSYS Workbench中，进行静力学分析。采用四面体网格和六面体网格对重载机械臂分块进行划分，以提高网格质量。

图1 重载机械臂结构示意图

重载机械臂最大工作负载为1500kg，整个臂架的长度l为5.83m。各部分材料均采用45钢，屈服强度为355MPa，取安全系数[7]为1.34，则许用应力为263MPa，许用刚度[7]f=0.1l2=3.4cm=34mm。

1.2 工况分析

机械臂工作时，最大负载量为1500kg，伸缩臂全部伸出时长度为4.015m，臂的俯仰角在-35°～45°范围内变化。为确定危险工况，选取伸缩臂全部伸出且满载时，俯仰角分别为0°、45°和-35°时的三种工况进行静力学分析，其他工况介于这三种工况之间，不做讨论。

1.3 仿真结果与分析

由分析结果可知，重载机械臂俯仰角为-35°时为危险工况。图2(a)为机械臂变形云图，最大变形位于重载机械臂抓手顶端，为19.93mm，小于许用刚度，刚度要求满足。

图2(b)为机械臂等效应力云图，最大应力位于滚摆马达与进退滑块相连接的局部，为482.07MPa，超过了45钢的许用应力，由于该处模型几何尺寸不连续，应力产生奇异，以此作为强度校核依据显然不合理[8]。并且根据塑性强化理论，该处应力不会线性增加。采用ANSYS Workbench的应力线性化工具进行处理，去除应力奇异引起的峰值应力，保留名义应力。此时最大等效应力为174.17MPa，满足强度要求。

由图2可以看出，伸缩臂最大等效应力为118.56MPa，最大变形为11.28mm，小于伸缩臂的许用刚度为16.2mm，强度和刚度都存在较大冗余，因此，本文以伸缩臂质量最小为优化目标，对其截面尺寸进行优化设计。

图2 静力学分析结果图

2 结构优化设计

伸缩臂截面形状如图3所示，选取翼缘板厚度S、半径R和腹板厚度X作为设计变量，其变化范围分别为4mm～8mm、10mm～20mm和4mm～8mm，将伸缩臂质量M作为输出变量[9]。

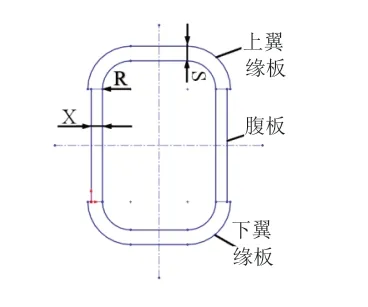
图3 伸缩臂截面示意图

2.1 Box-Behnken试验设计

采用Box-Behnken试验设计方法，应用Design Expert软件对伸缩臂截面尺寸进行三因素三水平试验设计，得到13组参数组合，如表1所示。

表1 试验设计组合

对表1中试验设计参数组合分别进行静力学分析，得到13组样本对应的质量M。构建响应面函数采用含有交叉项的二次多项式，通过最小二乘回归分析[10]，得到响应面函数：

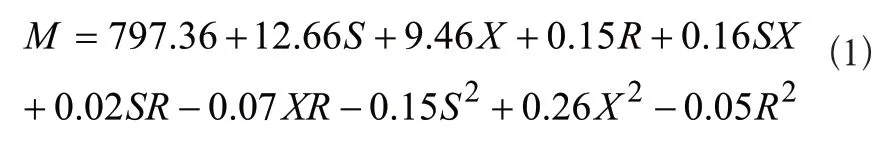
通过方差分析得到响应面模型受不同因素的影响情况，质量M方差分析结果如表2所示。若p值小于0.05则认为影响显著，去除不显著项，式(1)可简化为：

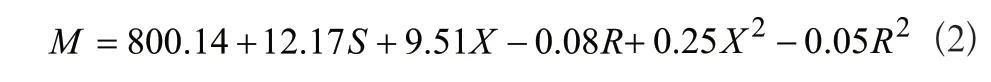
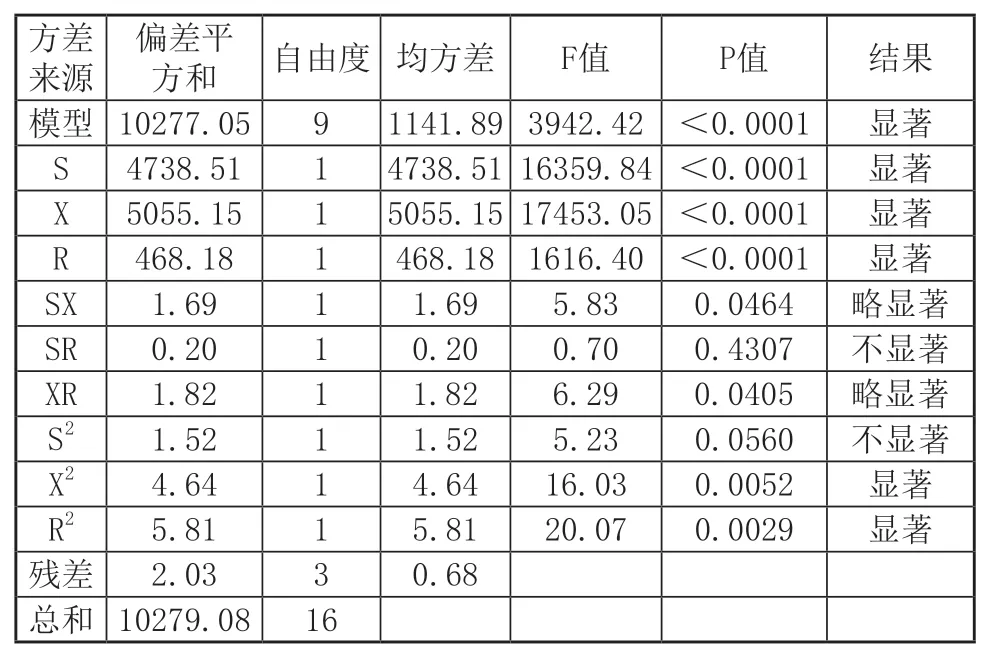
表2 M方差分析结果

响应面模型相关系数的平方R2为0.9998，大于0.95，说明响应面模型拟合得很好，能够很好的预测输出变量与设计变量之间的关系。

通过Box-Behnken试验设计点拟合响应面，可以得到对伸缩臂性能影响较大的关键尺寸对伸缩臂质量、变形和应力的变化规律，如图4所示。可以看出：尺寸参数S、X、R与伸缩臂应力、变形和质量成线性关系，其中参数S与质量成正比，与应力和变形成反比。R与应力和变形成正比，与质量成反比，但影响程度小于S、X。参数X与质量成正比，对应力和变形影响不大。说明减小伸缩臂相应尺寸参数可达到轻量化的效果，但重载机械臂应力与变形会有所增加。

图4 响应面关系图

2.2 响应面优化

以式(2)作为目标函数，以参数S、X、R的取值范围为约束条件，建立优化模型[11]：

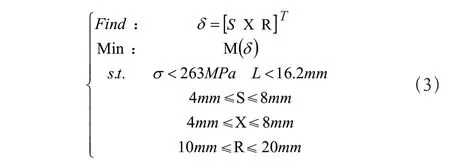
式(3)中：δ为参数组合函数；M(δ)为目标函数；σ为伸缩臂最大等效应力；L为伸缩臂最大变形量。

采用响应面优化算法搜索使伸缩臂质量最小的尺寸参数，得到最优尺寸参数组合为δ=[7 4 20]T。

根据伸缩臂优化尺寸，重新建立重载机械臂的有限元模型，进行静力学分析，所得结果与优化前的仿真结果如表3所示，可知，伸缩臂的质量比优化前减轻了65.1kg，伸缩臂的变形及最大应力较优化前略有增加，但强度和刚度仍有一定的冗余。伸缩臂优化后，重载机械臂的强度和刚度也满足要求。

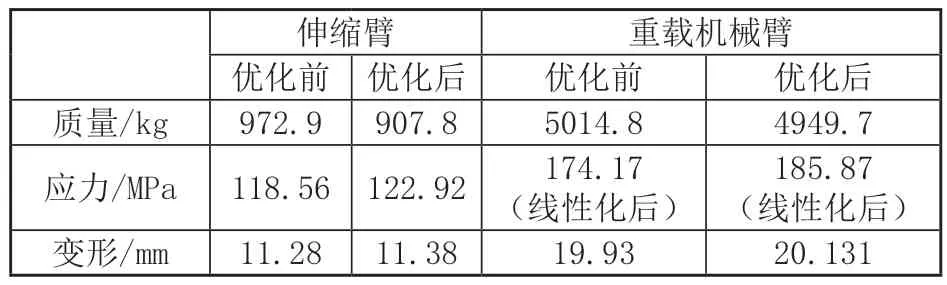
表3 优化前后质量、应力和变形量对比结果

3 重载机械臂轨迹误差

将重载机械臂危险工况的三维实体模型导入到ADAMS软件中，对样机几何模型添加约束、载荷，得到重载机械臂多刚体模型，如图5所示。运用ADAMS/ViewFlex模块将模型中关节柔性化，得到重载机械臂刚柔耦合模型。确定仿真轨迹，利用step函数添加运动驱动，对重载机械臂刚柔耦合模型的运动轨迹进行仿真[12]，得到重载机械臂末端实际位移。将实际位移与期望轨迹位移做比较，得到轨迹总误差，如图6所示。对比优化前后轨迹总误差，由7.77mm降到1.67mm，明显提高了重载机械臂的轨迹精度，也验证了该优化方案的可行性。

图5 多刚体模型简化图

图6 优化前后的重载机械臂轨迹总误差

4 结语

1）利用ANSYS Workbench软件对重载机械臂的三种典型工况进行静力学分析，由应力和变形云图，得到最危险工况，强度和刚度满足要求，且伸缩臂有较大冗余。

2）以伸缩臂轻量化为目标，对伸缩臂截面的关键尺寸参数进行优化设计。采用Box-Behnken试验设计得到伸缩臂截面的最佳参数组合，采用响应面优化方法，在满足伸缩臂强度和刚度前提下，伸缩臂质量减少了65.1kg，减轻了重载机械臂自身质量，降低了成本。

3）对重载机械臂刚柔耦合运动轨迹进行仿真分析，优化后的轨迹总误差较优化前减少了6.1mm，提高了轨迹精度，验证了优化结果的可行性。