基于SLP和AHP的输液器组装车间布局优化及仿真
2022-05-12黄鹏鹏魏春珊郑雅琳
黄鹏鹏,魏春珊,郑雅琳
(江西理工大学 机电工程学院,赣州 341000)
0 引言
设施布局的优劣决定了生产效率和生产成本的高低,并且被认为是仅次于增加新设备节约投资的关键性措施[1]。特别医疗器械生产行业中对车间无尘化要求较高。科学有效的设施布局能够减少物料在流通过程中的等待和搬运时间,节约生产管理成本,缩短产品周期,有效提高生产能力。
宁芳等采用SLP从物流、人流与应急部门的关联进行分析,通过加权因素法对优化前后的设施建筑布局评价[2]。周佶睿等在SLP的基础上,仅采用物流—距离分析法从物流成本角度比较布局方案,存在一定的局限性[3]。一些学者运用SLP和AHP结合得出最佳方案,为设施布局的选择提供了一种新的方法,但没有进行仿真验证[4~6]。周尔民等通过对福州台钻厂的基本要素分析,运用SLP法进行平面布置优化,利用Em-plant仿真验证了模型的有效性[7]。彭飞等采用SLP法和Plant Simulation仿真,对多品种小批量的高铁小部件生产车间进行产线工艺规划,可有效弥补SLP法的不足[8]。侯智等以搬运总费用和总面积最小为目标,采用SLP和遗传算法相结合的方式对仓储布局进行优化,弥补了遗传算法易陷入局部最优的缺陷[9]。
基于前人的研究成果,本文针对A公司输液器组装车间的特点,通过运用SLP和AHP方法,考虑实际约束条件,确定优化布局方案,再采取Flexism仿真软件验证了优化方案的可行性。该套方法体系对其他设施布局优化提供一定参考意义。
1 基于SLP输液器组装车间布局分析
组装车间作为输液器生产的核心,共有六条生产线,包括袋式、普通型、止液型和避光型这四条人工组装线以及B3型全自动组装线和输液针全自动组装线。市场需求条件下,公司需要引进大型全自动化B3输液器组装机及输液自动组装机、滴斗自动组装机等。由于车间面积有限,为提高车间物流效率,所以需要对车间布局进行更系统的改善,其中输液器车间照各作业单位的代号及尺寸如表1所示,接下来的图中均用代号表示各区域单位名称。
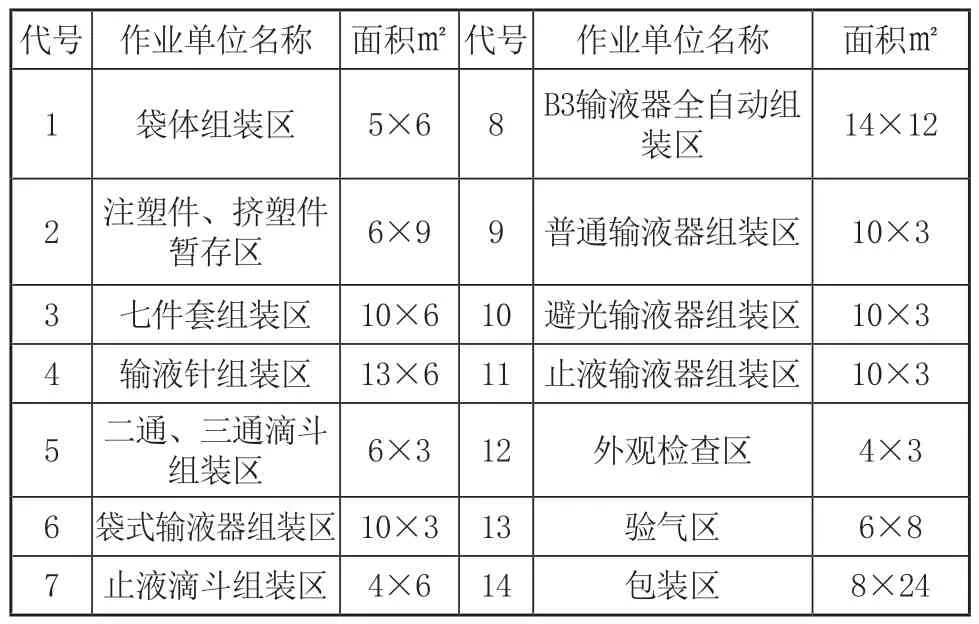
表1 各作业单位代号及尺寸表
采用“曼哈顿距离”计算各作业单位之间的距离,根据各类产品的工艺路线和年产量以及在各类在制品的重量可以计算出年物流量,将物流量和距离的乘积量距积作为衡量物流强度的指标,结果如表2所示。
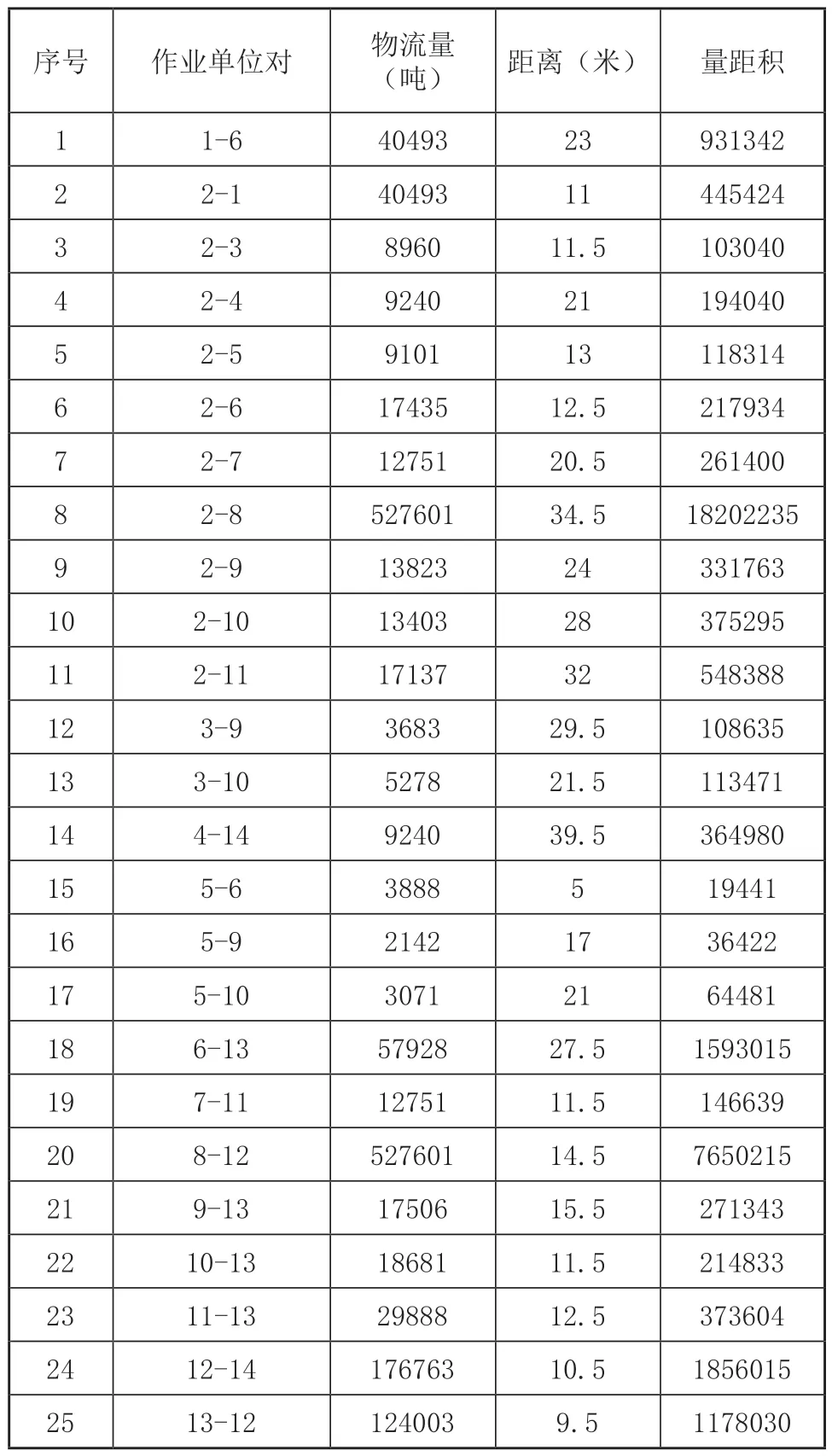
表2 各作业单位间物流量距积
由于直接分析大量物流数据比较困难且没有必要,可以用如表3所示的物流强度等级划分表来确定作业单位间物流强度。
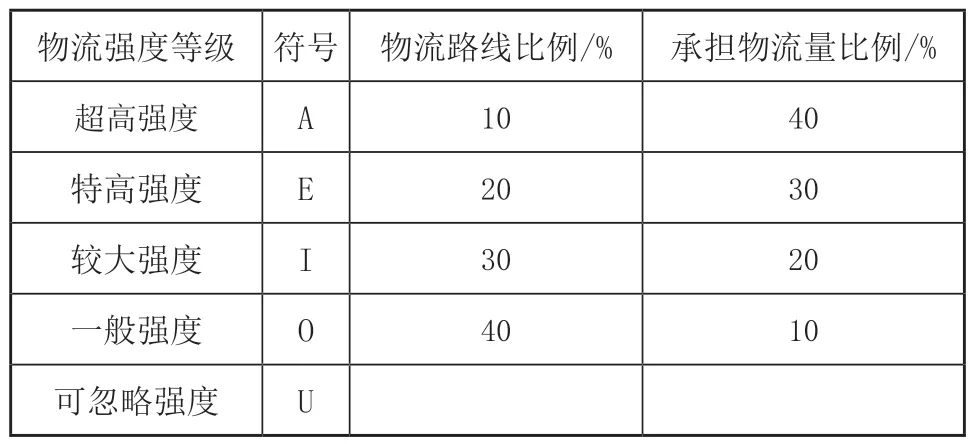
表3 物流强度等级划分表
对表2的量距积降序排列,再结合表3的物流强度等级,建立各作业单位物流强度分析表如表4所示。
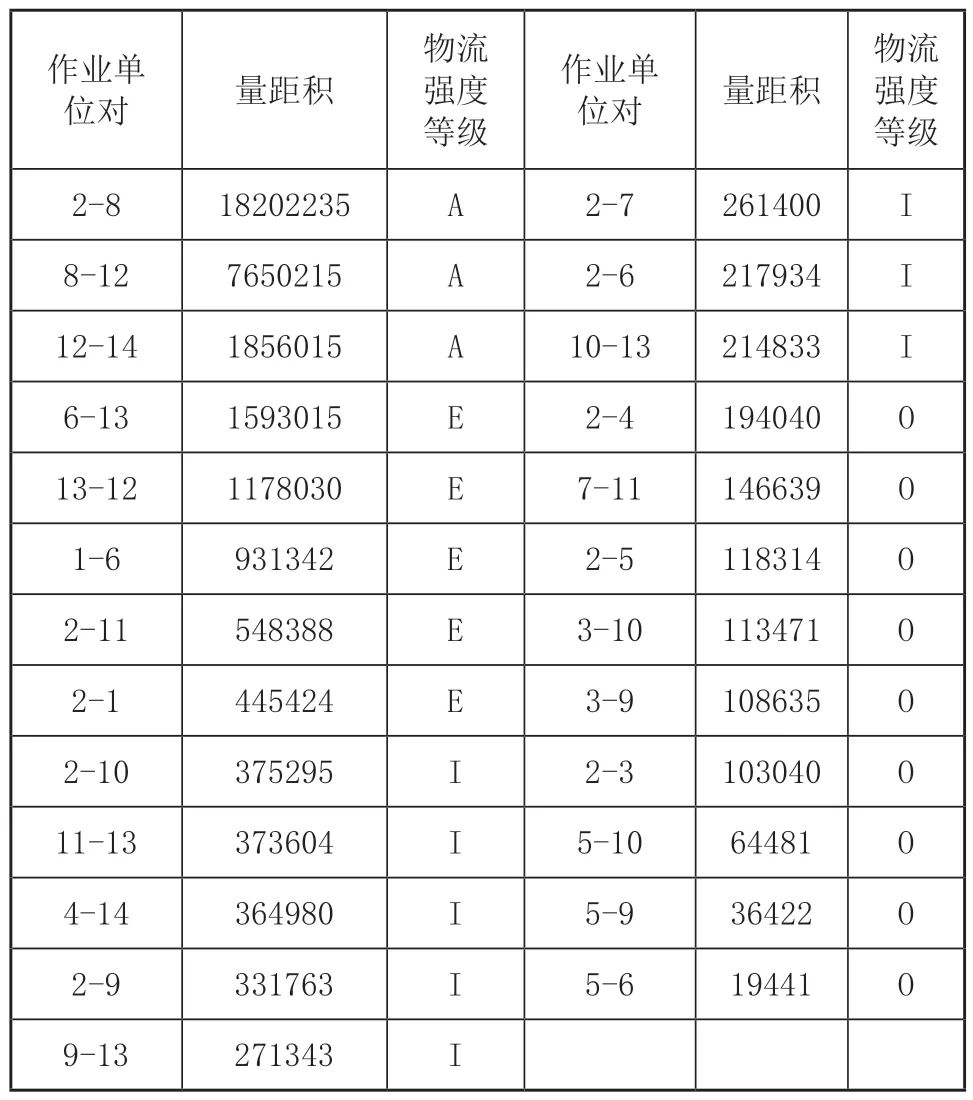
表4 各作业单位物流强度分析表
非物流关系与物流效率密不可分,非物流关系分析主要考虑工作流程的连续性、生产服务、物料搬运、管理方便、安全及污染、共用设备及辅助动力源、振动和人员联系之间的密切程度[10]。
结合输液器组装车间的实际情况,按照物流与非物流加权值为1∶1对得出的作业单位物流强度等级和非物流关系密切程度等级进行计算。不同的物流强度等级和密切程度等级对应着不同的分值,取A=4,E=3,I=2,O=1,U=0,X=-1。建立各作业单位综合相互关系图如图1所示。
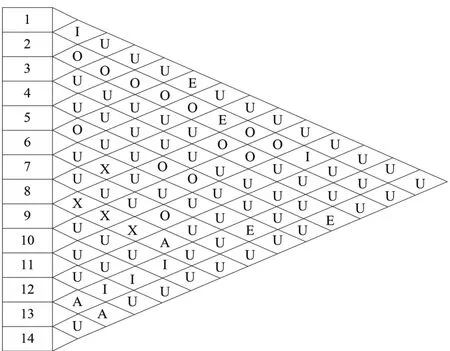
图1 各作业单位间综合相互关系图
由图1可以清晰看到各个作业单位间的相互综合关系,如为A级的作业单位对有3对,分别是8和12、12和13、12和14。
综上对作业单位间关系进行分析,绘制车间作业单位面积相关图如图2所示。
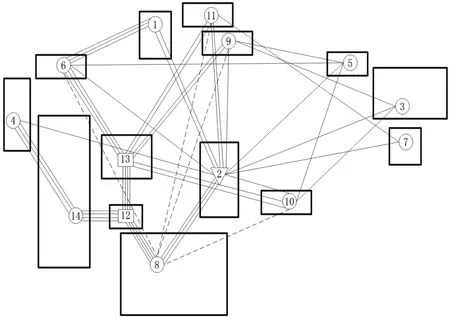
图2 作业单位面积相关图
根据作业单位面积相关图,并参考车间实际可用面积,各设施之间的最小间距等作出改善后的设施布局方案如图3、图4所示。由于每平方米的建设及维持成本远高于一般车间,故方案一在布局时考虑增加较大的预留面积;同类型产品生产过程的高连续性可降低物流成本,故方案二在布局时着重考虑缩短生产同种类型输液器的各作业单位之间的距离。其中方案一、方案二布局图中虚线下方空白部分为优化布局后减少的占地面积。
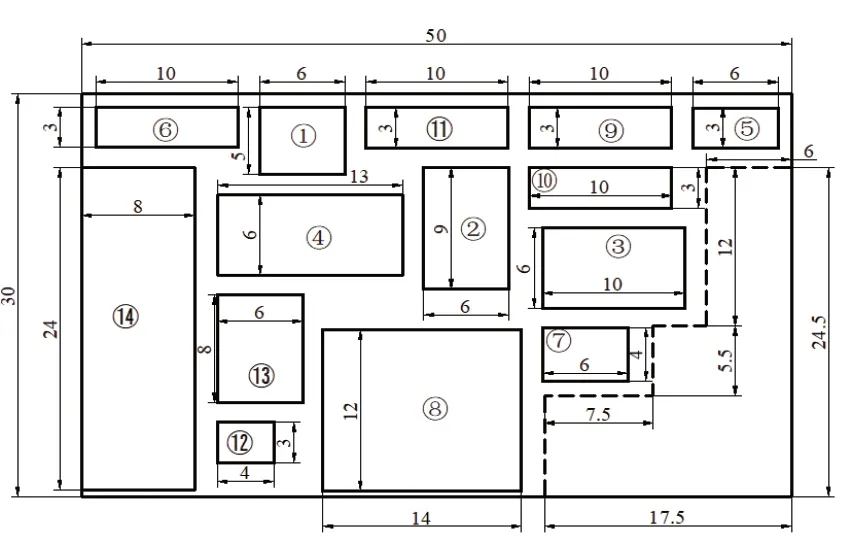
图3 优化布局方案一
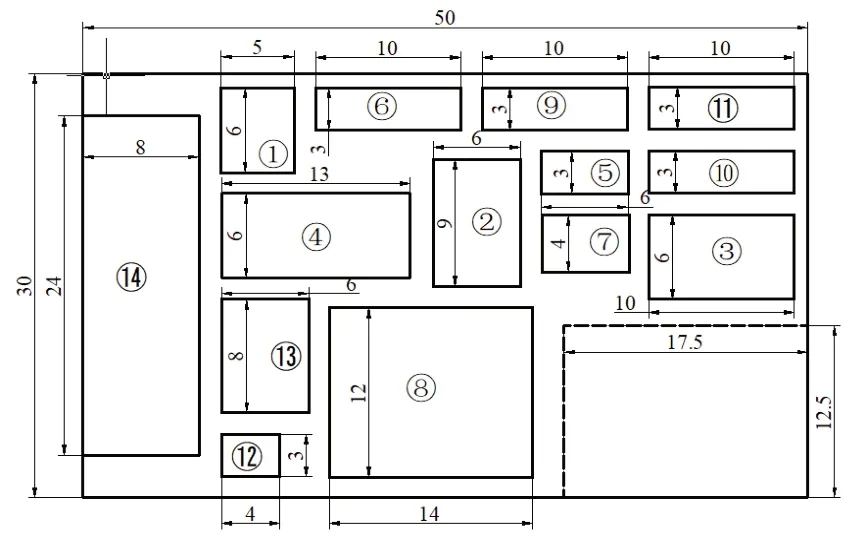
图4 优化布局方案二
根据得出的布局方案图,按照车间之前月净化成本为42元/m2计算年净化成本,按照表4所示方式可计算出改善方案量距积,结果对比如表5所示。
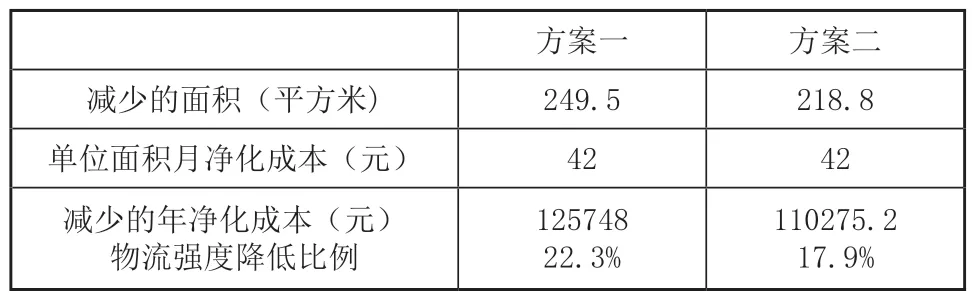
表5 方案对比表
2 基于AHP对布局方案决策评价
由表8可知,方案一与方案二的占地面积基本相等且物流料搬运量距积均小于原始布局方案,方案一的物料搬运量距积却小于方案二,但不能就此得出方案一即为最佳布局方案的结论。本节将采用层次分析法从净化成本、物流效率、质量控制、工作环境和设备利用率等多个角度分析输液器车间原始布局与改善方案的优劣,选择出最合适的布局方案。
2.1 构建层次分析模型
根据输液器组装车间设施布局方案,运用AHP法首先明确决策目标,再对系统各个相关因素进行分析,构建特定的层次结构模型如图5所示。
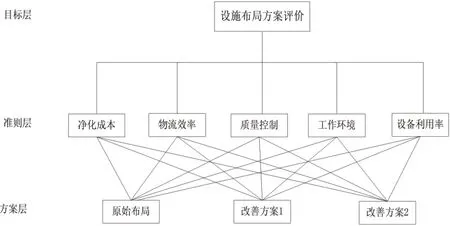
图5 车间布局层次分析结构模型
2.2 构建判断矩阵
把准则层的元素两两比较,根据9级标度法对照元素标度表给准则元素的重要程度进行打分。分数主要利用专家询问法和问卷调查法得出,分值按照如表6所示的元素标度表进行评定。
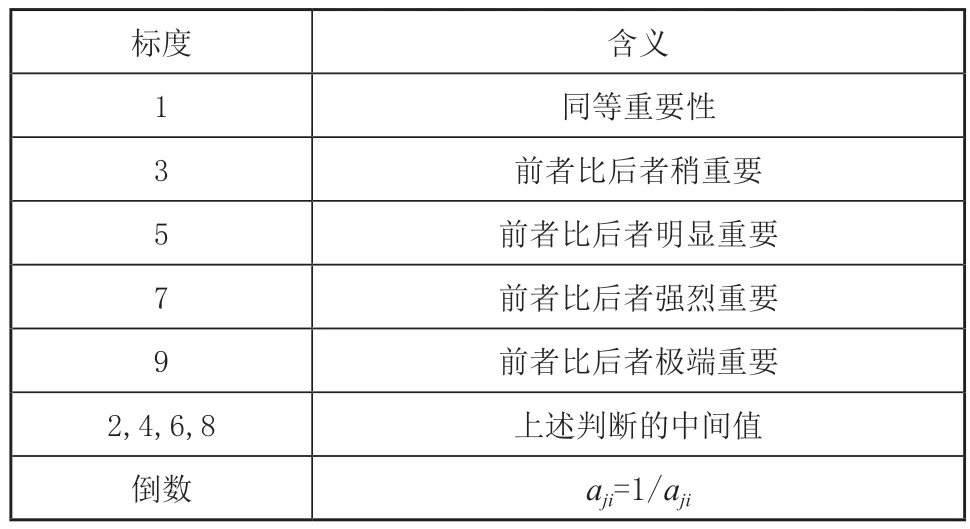
表6 元素标度表
选取10位专家及技术相关人员对每项对比准则打分,取所打分值的众数为该项的最终分值,可得到矩阵如下:
1)准则层对比目标层的判断矩阵:

2)方案层对准则层的判断矩阵:

2.3 层次单排序及一致性检验
1)由MATLAB可得准则层对比目标层的判断矩阵的最大特征值λmax=5.32,特征列向量:

根据一致性指标一致性比率的计算公式得出:
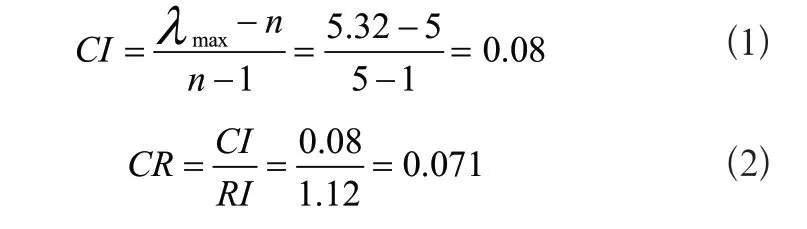
CR=0.071<0.1,表示该判断矩阵通过了检验。
2)由MATLAB程序求解可得方案层元素相对物流效率的判断矩阵的最大特征值λmax=3.04,特征列向量:
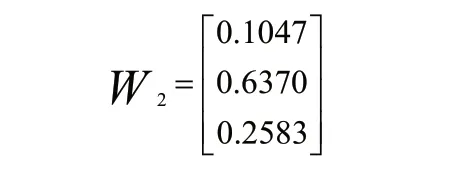
根据一致性指标和一致性比率的计算公式得出:

CR=0.03<0.1,表示该判断矩阵通过了检验。
由于方案层元素相对准则层其他元素的计算方式与物流效率相同,可以相同的计算方式得到方案层各元素相对准则层各元素的特征向量权重为:

2.4 层次总排序及一致性检验
层次总排序计算过程如下:

计算结果为:
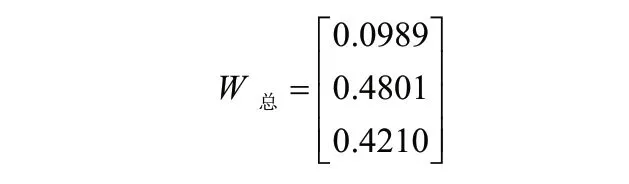
通过层次总排序特征向量可以看出,方案一分数最高,其次为方案二,最后为原始布局。因此方案一为最佳设施布局改善方案。
3 仿真验证方案
上节采用AHP评价,确定方案一为最佳布局方案。由于方案实施需要一定的成本,得出改善方案的最优性和有效性目前只在理论层面上成立。为了直观看出改善后的设施布局是否满足企业实际生产要求,采用Flexsim仿真软件对最优布局方案进行生产模拟。
3.1 条件假设
为了防止计算机仿真建立的模型产生更多误差,在进行仿真前需要对生产条件做出如下假设。
1)输液器生产车间一共生产B3输液器、袋式输液器、普通输液器、避光输液器和止液输液器五种类型产品,生产方式为按订单生产,不考虑库存量。
2)生产期间暂存区物料供应充足,且由于原始方案与优化的两个方案中设施设备的故障率没有发生变化,所以直接假设机器设备无故障。
3)不额外添加操作员和搬运人员,处理器加工产品代表工人在操作,产品在作业单位之间的流动代表工人搬运物料。
4)模拟6天工作时间,每天工作8h,因此仿真总时间为216000秒。
3.2 数据收集
完成生产条件假设后,收集输液器组装车间生产数据如表7所示。
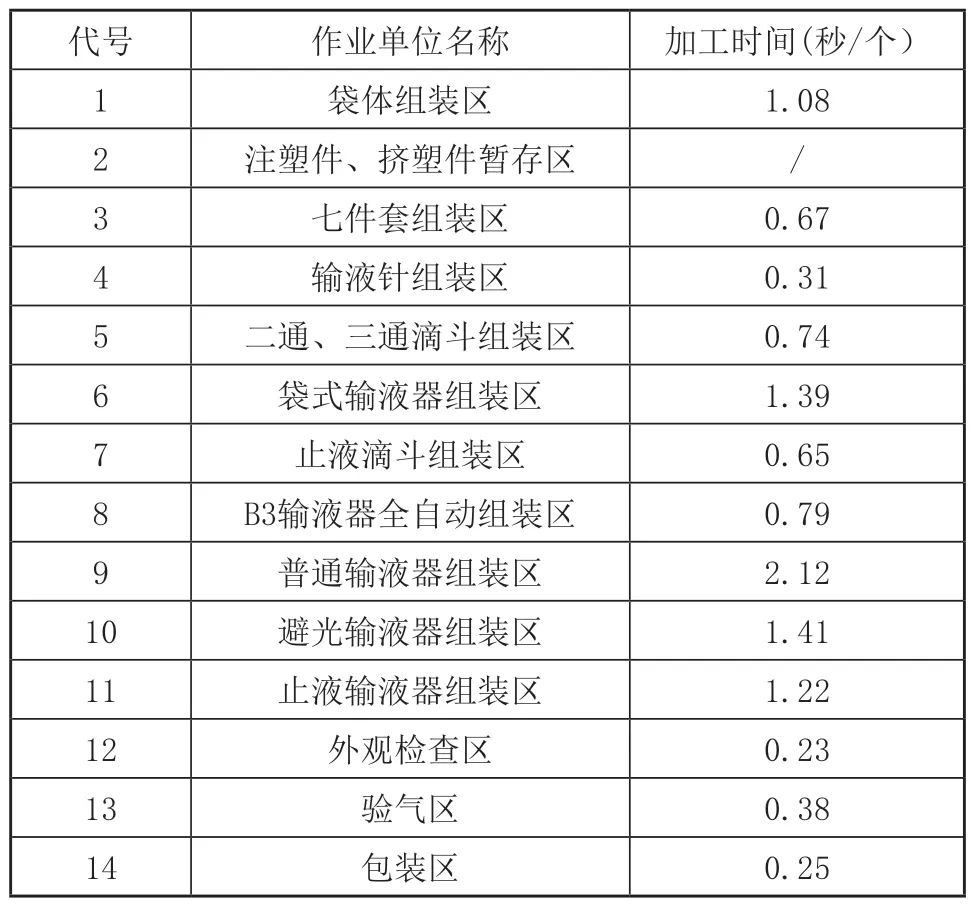
表7 各作业单位加工时间表
3.3 建立仿真模型
根据A公司输液器组装车间的实际生产情况,运用Flexsim软件建立仿真模型如图6所示。
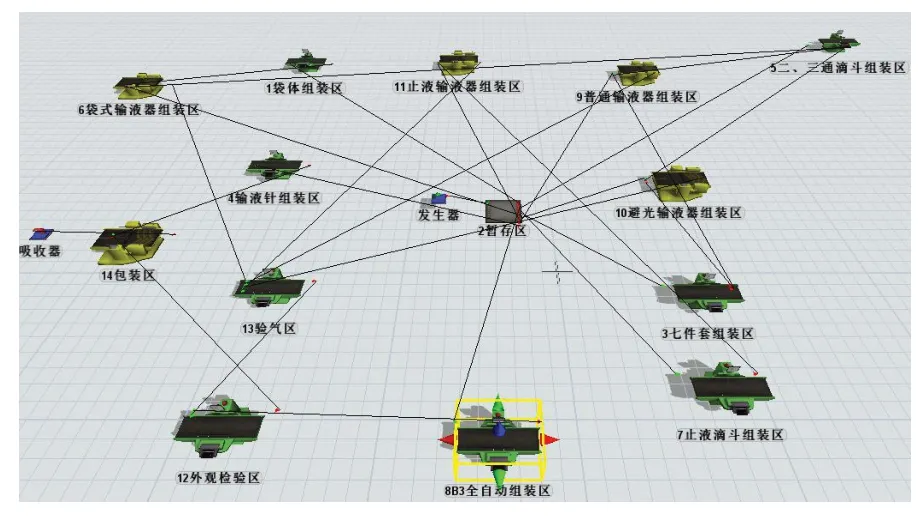
图6 仿真模型布局图
3.4 仿真结果分析
设置完各实体参数待运行结束后,可得到仿真结果报告如表8所示。
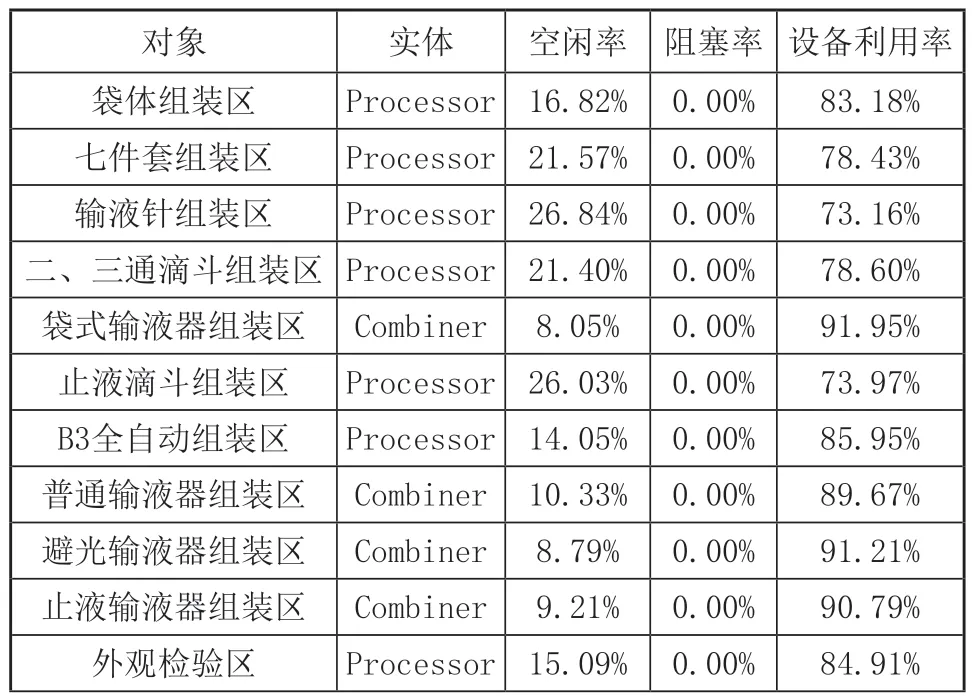
表8 仿真结果统计表
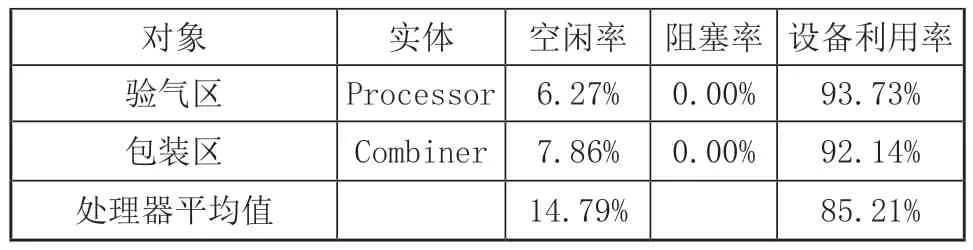
(续)
从表7可以清晰看到,改善后组装车间的平均设备利用率为85.21%。其中输液器手工组装线的设备空闲率较低在10%以下,设备利用率较高在90%以上。表明改善后的设备闲置较少,设施布局满足企业实际生产要求,有效利用了现有资源为产能效力。
4 结语
1)运用SLP法对输液器组装车间设施布局进行优化设计,结合工厂设施的现实条件约束获得两个优化方案,优化方案在成本和物流强度方面均有较大降低;
2)为选出最佳优化方案,通过运用AHP法从多个维度评价方案证实优化方案具有理论可行性,同时采取Flexsim仿真模拟实际生产证实优化方案具有实践可行性;
3)本文分析方法及体系具有通用性,只要对优化对象和作业单元进行调整后,就可应用于其他布局优化车间。
