木结构组合墙体自动装配系统的研究

陶承宗，陈海卫,2*，陈延斌

（1.江南大学 机械工程学院，无锡 214122;2.江苏省食品先进制造装备技术重点实验室，无锡 214122)

0 引言

近年来，随着生活水平的提高及全球低碳环保理念的盛行，人们更加追求建筑材料的环保性和建筑物功能的多样性[1]。现代木结构建筑凭借抗震性好，艺术表现性强，较其它建筑材料有噪音低，尘土少，废水污染小等优点[2]，一直受到人们的关注。木结构组合墙体作为木建筑的主体，在载荷承受、防潮、保温、隔音等方面有很高的要求[3]，因此生产商对墙体的生产加工装配过程格外重视。目前，墙体生产过程存在自动化程度低、装配路线规划不合理的局面，亟需研制一款以装配序列规划为核心的自动化装配系统去改善这样的生产现状。国内外在该领域有很多深刻的研究，美国VRCIM实验室与美国NIST合作开发的虚拟装配环境VADE[4]能自动从CAD系统中自动提取模型的几何、物理属性，通过戴头盔人机交互的方式实现产品的自动装配工艺规划。秦锴[5]利用拆卸法思想对装配模型进行装配序列规划，用全回转推进器的实例验证了所开发装配系统的有效性。张强[6]通过利用实时拆卸运动仿真跟实时干涉检验的方式求得装配序列，成功实现HCW轧机的虚拟装配。彭敏[7]利用SW的二次开发提取出装配体模型矩阵信息，结合干涉矩阵的特性自动生成装配顺序，最后成功实现一级圆柱齿轮减速器的自动化装配。Remeo M.Marian[8]等对改进型液压直线电动机建立连接表，干涉表模型，利用GA算法对序列群优化，实现了电机的装配工艺的改良。李慧[9]针对机器人自动化作业的需求，设计了机器人自动装配系统，实现了产品的装配信息建模、装配序列规划及装配路径规划的功能。

本文针对墙体的生产装配环节，首先设计了墙体的柔性装配方案，之后对墙体模型进行底层分析和数字化建模，之后基于拆卸法思想进行墙体的装配序列规划；而后构建了基于机器人运动行程的评价指标数学模型，对序列群综合评价筛选出了最优序列，使墙体的装配任务得到了优化。

1 墙体模型的分析

本文研究的木结构组合墙体，主要是由托梁、底板、顶板、带板、过梁等横截面相同，长度不同的木板构成，如图1(a)所示，零件木板没有凹槽，卡口部件，采用的装配方式是传统的多块木板的直接钉钉。根据墙体装配图以及墙体装配的技术要求，由研究人员设计，得到如图1(b)所示的墙体模型。

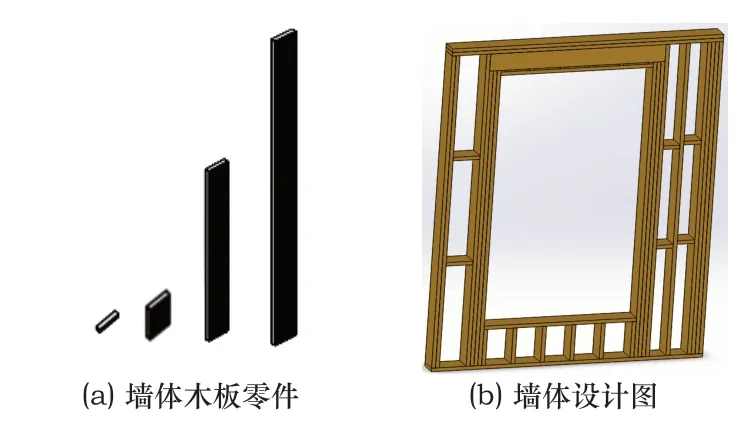
图1 墙体组成零件及设计图

墙体的装配过程主要分为上料、运料、定位、装配几个环节，而系统主要由龙门机床、工业机器人，运料传送带、光纤传感器、PLC控制器以及一些非标设备构成。首先搬运机器人将木板由载物台运送到传送带，之后采用运料传送带实现木板运料，利用龙门平台将木板零件运送到工作台，利用三台工业机器人跟龙门平台配合完成整个打钉操作。装配方案如图2所示。

图2 墙体的装配系统图

装配系统建立之后，需要对墙体模型本身进行底层分析，采集出模型基本信息，从而为装配工艺生成奠定基础。对于给定的墙体模型，由于初始模型只是木板布局图，并没有给明打钉的情况，所以首要工作就是判定打钉的状态，因两板贴合是两板可打钉的必要不充分条件，第一步也就是分析板与板的贴合状态，从而初选出打钉位置。

对于两面贴合，有如下充要条件：

1）面与面的距离为0，即两面重合；

2）实体中面与面的外法向量方向相反，或者面与面的不包含边界的矩形区域存在交集；

本文采用重合跟面面区域存在交集的方法判断贴合。设存在面S1与S2，它们位于XOY平面且位于不同的部件：

ymin跟ymax定义类似x，则两面贴合的充要条件为：

通过solidworks的API进行二次开发，完成装配体信息的提取。利用Feature：：FirstFeature()和Featu -re：：GetNextFeature()按特征树顺序遍历零件，通过Component2：：GetBodies2获取对象的实体，再通过实体跟Face2：：GetFaces()获得所有面信息，利用Assem -blyDoc：：ClosestDistance筛选出不可能贴合的部件，利用Measure：：NormalDistance测量面面距，结合Measure：：IsPerpendicular进行筛选出垂直面，再通过Face2：：GetEdges()获得面的边信息，通过边信息跟Edge：：IgetStartVertex()就可以获得边的起始向量信息，通过Vertex：：GetPoint()获取局部坐标系下的点坐标，再通过 MathPoint：：MultiplyTransform的方法去实现变换，从而转换成全局坐标系下的坐标，进行坐标的冒泡排序后再根据(5)设计贴合程序，从而提取出相应的贴合信息。

在贴合信息提取完成的基础上，需进一步分析墙体的打钉面的位置，打钉的位置及打钉的个数，完成整个墙体模型的打钉附属工艺的初步规划，从而为装配序列规划奠定基础。

在贴合面的基础上，与贴合面间隔一个板厚距离的面即为打钉面。当仅存在一个打钉面时，打钉面即为此面。当存在二个打钉面时，根据装配体的方位选择打钉面，打钉区域位于整个装配体左侧，那打钉方向往右边，若在装配体右侧则往左边打钉，若为上边则往下打钉，若为下边则往上打钉。而打钉位置则在贴合面交集区域形心的基础上，根据贴合面交集区域的面积大小，设置合理的长、宽方向间隔进行网格化打钉。

如图3所示，设两面在XOY平面下贴合，两贴合面的z坐标相同，令z=zsame，

图3 贴合面交集区域形心图

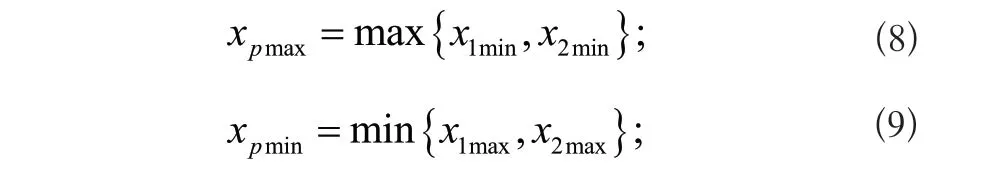
ypamx与ypmin的定义类似xpmax与xpmin，则形心坐标(x0，y0，z0)可表示为：

若x方向设定打钉间隔为Δx，y方向为Δy，那么该贴合区域打钉个数N可以表示为：

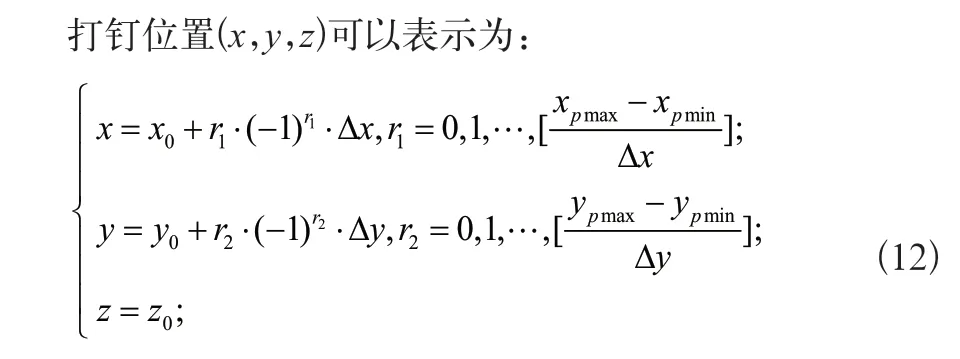
结合Assembly：：AddMate5和Assembly：：AddC -omponent5的API，设计程序可以自动完成墙体打钉分析，生成打完钉后的墙体模型。

2 墙体的装配序列规划及评价

针对打完钉后的墙体模型，做适当编码处理后，便要寻找合理的表达方式充分表达该墙体的模型信息，从而便于生成装配序列。常用的模型有AND/OR图，节点图等表达方式，但便于计算机处理的仍然是矩阵模型。

针对多紧固件装配体模型，这里给出了紧固件连接矩阵模型和紧固件阻挡矩阵模型来表达模型。设打钉后的墙体有n个木板零件，m个紧固件，行代表紧固件，列代表木板零件，编码规则是装配体所有零件号码为1∶n+m，1∶n代表木板零件，n+1∶n+m代表紧固件，紧固件号=矩阵行号+n；则紧固件连接矩阵FAM中的元素aij：

紧固件阻挡矩阵FAM中的元素bij：

装配序列规划(Assembly Sequence Planning)，即在装配体几何约束的条件下找出一条或多条满足几何可行性和在建立一系列评价准则后经综合评价并筛选出评价值最好的装配路线过程。而拆卸法的思想只需考虑单方面的约束，因为已拆卸的零件不会干涉后面零件的拆卸，相比于装配的双向约束，拆卸法一定程度上简化了ASP问题的求解难度[6]。紧固件作为特殊的零件，如果在ASP问题中忽略紧固件而单纯的研究零件的装配序列，这样会忽略重要的模型信息，导致求解出来的序列解不一定满足几何可行性，如果考虑所有的紧固件将会导致理论解为n+m个，将会产生组合爆炸问题导致求解速度很慢[10]，因此需要对紧固件进行特别处理。紧固件跟其连接的零件存在一种内在的隐藏优先关系，在实际工程经验中，一般先拆卸紧固件，在拆卸紧固件所连接的零件，通过建立紧固件与跟其连接零件的内在绑定关系，将大大缩减ASP问题的规模，节省规划时间。

在已知FAM和FCM条件下求解ASP问题的步骤如下，定义存放序列的数组xulie初始等于φ：

Step1：根据FAM找出未被阻挡的紧固件qi，qi对应的零件号为Si，将所有的qi存放于数组k1；

Step2：遍历k1数组的元素，根据qi代表的行号搜索矩阵FCM，在该行存在所有为1的列Aj中，对FCM的Aj列求和，若值等于1，将所有的Aj存入数组k2，按顺序取出k2中Aj，Aj对应的零件号为Sj，则分别将Si和Sj加入xulie，若不存在和等于1，则返回k1数组的下一个元素，重复Step2；

Step3：删除矩阵FCM和FAM中qi和Aj对应的行或者列；

Step4：重复Step1，Step2，Step3，如果FAM的行数等于零，则输出xulie，否则继续重复；

Step5：遍历所有数组k1跟k2元素，输出所有xulie解，将xulie倒序，即为装配解。

在生成满足几何可行性的序列后，需要建立合理的评价指标对序列群进行综合评价，选出最节省装配时间的装配工艺指导生产实际。

传统的装配序列评价指标包括几何可行性、装配方向改变次数、装配工具的改变次数，装配体稳定性、聚合性等。在墙体生产过程中，影响最重要的因素就是墙体的装配时间。研究表明：产品装配所需工时占产品生产制造总工时的40%～60%[5]。由此可见装配时间的提高对产品的高效率生产有着至关重要的影响。所以对于本墙体，拟采用机器人的运动行程作为评价指标。

机器人的运动行程包括龙门平台运料行程、机器人打钉行程、机器人辅助定位行程。而机器人的运动行程具体可以表征为距离。常用的距离模型包括欧氏距离、曼哈顿距离、闵可夫斯基距离、马氏距离等，本文利用欧式距离衡量机器人的运动行程。

对于生成的各个装配序列，由于墙体各个零件的安装位置固定，所以每个序列的龙门平台从开始运料到摆放木板零件到相应位置的运动行程和都是相等的；同理，机器人的辅助定位行程和也是相等的，最关键的因素即机器人的打钉行程。该打钉行程优化模型类似于TSP旅行商问题，即一个邮递员如何找出最短路径，使得他从邮局出发，给n个城市送完信件以后再返回邮局所走的路径最短。而本文的距离模型就是4个机器人在若干个打钉位置跟机器人原点之间的TSP问题。

设D(Pi，Pj)为点Pi和Pj的欧式距离，假设有n个打钉位置，P={P1，P2，...，Pn}为一条访问路径，Pn+1=P1为初始位置[11]，则每一条序列的打钉行程f(x)可以表征为：

其中i≠j；i，j∈{1，2，3，...nk}。

则本优化的模型可以表征为：

优化目标：minf(x)

优化条件：x∈Ω，其中Ω为所有满足几何可行性的序列集合。

3 实例分析

贴合信息为打钉信息奠定了基础，通过贴合信息进一步能得出打钉的位置，初步反映零件之间的位置关系，不仅表达两部件是贴合的，还能高亮显示贴合面，如图4所示。贴合信息的提取为打钉信息的生成垫底基础。

图4 零件贴合信息提取

贴合信息提取完成后，就要分析墙体的打钉信息。墙体打完钉后的效果如图5所示，能清晰地反映出打钉的面、打钉的位置及每一个打钉面打钉的个数等信息。

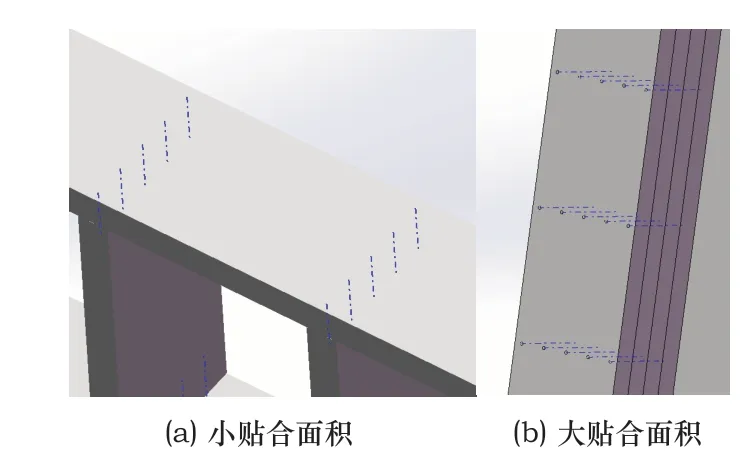
图5 不同贴合面积打钉情况图

针对打钉后的模型进行并行简化、编码等处理，如图6所示（括号内数字代表个数），从而方便装配序列规划工作。

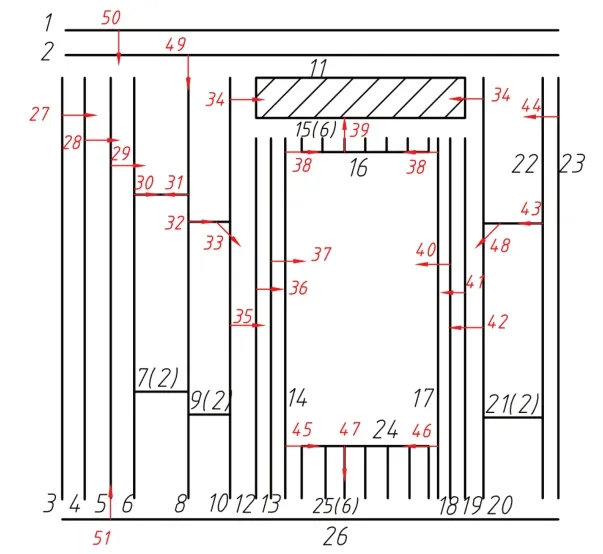
图6 打钉后模型编码后图片

在MATLAB环境下编程，对墙体采用第2节的方法进行装配序列规划，取零件24为初始装配件，通过实验共得到2412902个可行解，通过评价计算后共得到16组最优序列解，评价函数值为47.1293，综合装配资源等因素在16组解中选一组最优解如下：

24 14 45 17 46 25 47 16 38 18 40 19 41 20 42 21 48 22 43 23 44 15 39 13 37 12 36 10 35 9 33 11 34 8 32 7 31 6 30 5 29 4 28 3 27 2 49 1 50 26 51。

针对该最优装配序列进行演示，演示结果如图7所示。

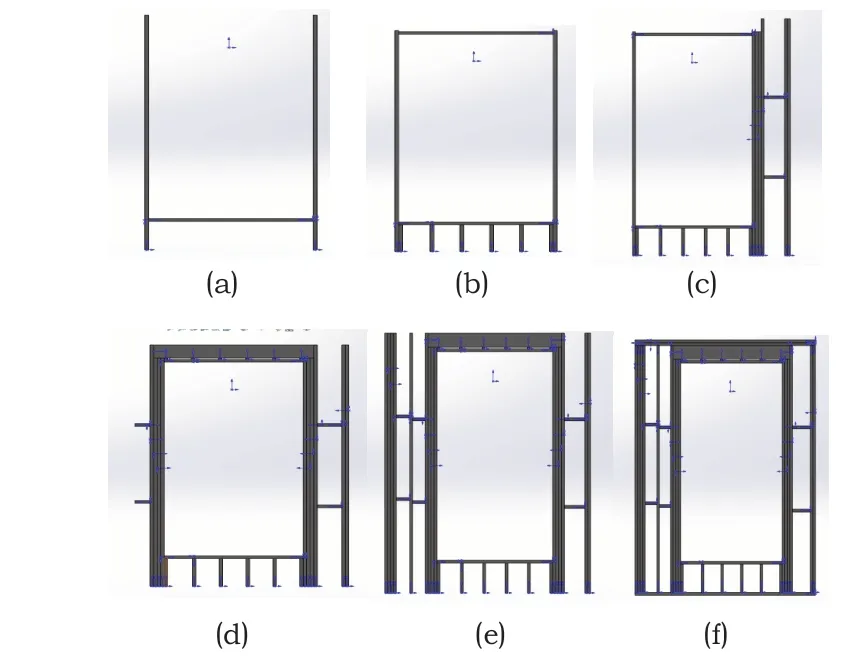
图7 最优序列的装配过程

4 结语

本文针对木结构组合墙体的产品报废率高，自动化程度低的生产现状，设计了一套包含装配方案、信息提取、装配工艺生成、工艺评价等模块的自动化装配系统、核心在于利用装配序列规划去改进墙体的装配工艺，产生的装配序列不仅满足几何可行性要求，而且经优化后的序列一定程度上减少了装配时间，提高了墙体的生产效率。并且从装配体底层分析、装配信息提取到装配序列规划、评价全由计算机完成，大大提高了木结构组合墙体生产的智能程度，为智能制造行业提供了一个典型范例。