县乡村多级生鲜果蔬电商物流节点布局与优化研究

□ 何立志，庞 燕

(中南林业科技大学 物流与交通学院，湖南 长沙 410004)

1 引言

在国家脱贫攻坚和乡村振兴政策的号召与扶持下，众多物流企业布局农村电商，生鲜果蔬产品线上消费需求越发旺盛。随着生鲜果蔬产量大幅增加，进一步打通农村生鲜果蔬产品“上行”进入城市消费的渠道成为城市消费者和农村种植户的共同愿景。但由于农村地区人口村落相对分散、交通设施不完善、建设资金匮乏、小农生产的农业模式依然存在，生鲜果蔬产品有序、及时“上行”进入城市消费还面临诸多困难。2019年交通运输部《推进乡镇运输服务站建设加快完善农村物流网络节点体系的意见》指出要大力推进县、乡、村三级物流节点体系建设，为农村物流基础设施建设提供了政策保障。合理构建县、乡、村多级物流节点，畅通生鲜果蔬“上行”渠道，提高“上行”效率和品质的研究既是对政策的响应支持也是农村经济发展的现实需要。

通过对近年国内外研究成果的总结，我们发现，在农村多级物流体系建设方面，武晓钊[1]对基于城乡对接的农村物流服务进行研究，提出构建覆盖“县、乡、村”的三级物流体系，黎红梅等[2]认为构建“县、乡、村”三级物流节点是降本提效的有效措施。梁潇等[3]对林果冷链“最先一公里”建设情况进行研究，为湖南林果冷链发展建言献策。汪子明[4]研究了农村物流网络建设的主要问题，并提出了改进措施。在农产品物流节点布局优化方面，窦志武等[5]总结了物流节点布局优化的模型方法与求解算法。Junnan Hua等[6]建立了海上生鲜果蔬物流节点配送优化模型，利用改进蚁群算法对节点配送进行优化。Liang Kaihao等[7]建立冷链物流节点优化模型，并给出算法求解。庞燕等[8]结合湖南新农村建设实践，建立了农产品物流节点优化模型,求解出物流节点优化方案。Javier Arturo等[9]基于多层次、多产品的运输需求，对山区易腐产品物流节点选址进行研究。李玉明等[10]通过TOPSIS算法求解模型提供了农村冷链物流节点布局最优方案。但关于“县、乡、村”三级物流节点的研究更多是在定性研究方面，而多级物流节点布局多是针对工业产品[11-12]，农村生鲜果蔬多级物流节点的布局研究并不丰富。本文将在前人研究的基础上，就农村多级生鲜果蔬电商的物流节点布局优化进行研究。

2 问题描述

农村发展果蔬种植，城市消费者在电商平台购买生鲜果蔬产品，各级节点要保质、高效完成生鲜果蔬运输任务，为此建设生鲜果蔬运输三级物流节点。首先，为提高节点服务覆盖率，降低成本，方便种植户快速邮寄果蔬产品，准备以村级供销合作社作为一级节点建设对象，一级节点布局优化前已知。其次，在各乡镇选择二级备选节点，负责汇集乡镇内或临近乡村的果蔬产品，产品汇集到本节点后向第三级节点运输。最后，在县域内寻找经济、交通优势较大的区域作为三级备选节点，负责汇集二级节点的货物，并向外部市场运输。本文主要研究生鲜果蔬产品到达县级节点的过程，到达县级节点后该过程结束。

在建设该三级物流节点时要考虑各级节点建设的数量和位置，使该多级物流节点运营总成本最低，以此得到最优布局方案。该多级物流节点布局结构如图1所示。

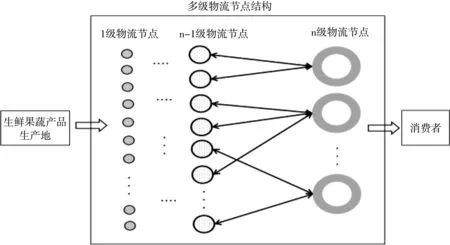
图1 多级物流节点结构图

3 模型构建

3.1 符号说明

3.1.1 参数说明

3.1.2 决策变量

3.2 基本假设

模型的建立满足以下假设：

①各级节点的生鲜果蔬产品运输需求必须得到满足且只能由一个上级节点来满足；②各节点熟悉当地运输路线，产品运输路线均为最优；③生鲜果蔬产品运输储存过程中保持适宜温度，且温度保持不变；④运输过程中不接受货物跨级运输。

3.3 成本分析

①建设成本。由于建设成本在运营前期占有较大份额，因此一次性将建设成本计算到模型运营成本当中显然会影响最终节点的布局优化。我们通过资金回收公式确定平摊系数：

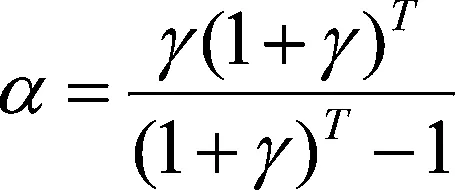
(1)

将建设成本平摊到规划使用年限当中。

根据参数设置和平摊系数可知每年需要投资的建设成本为

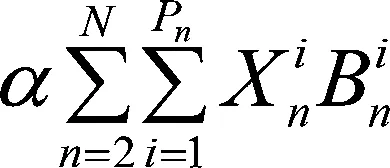
(2)

由于第一级物流节点以农村供销合作社作为载体进行建设，因此第一级物流节点无需投入实际建设费用，但是运营费用仍然存在，且与产品流通量相关。我们令

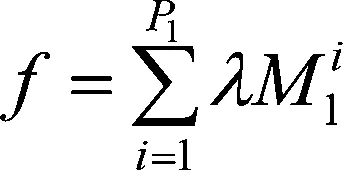
(3)

为第一级物流节点的建设运营费用。

②运输成本。运输成本的计算主要取决于单位质量产品节点间的运输费用和产品的运输质量，因此成本为

(4)

③储存成本。产品的储存成本包括两个部分，一个是仓库的固定运营成本，即不管产品是否存储，仓库也要支付的费用，另一个就是随产品储存活动发生而产生的可变成本，该成本由储存产品的多少来决定。其中，产品的固定储存成本可表示为

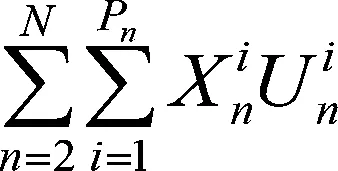
(5)

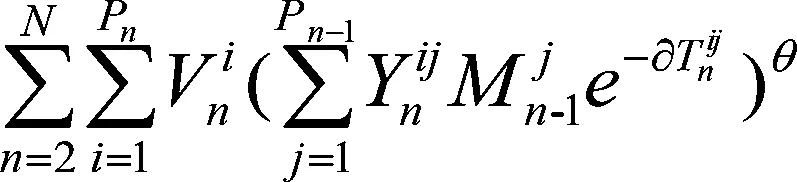
(6)

根据鲍姆尔-沃尔夫方法，θ与物流节点的规模有关，取值范围为θ∈(0,1)，一般情况下取值θ=0.5。

④损耗成本。受各个物流环节时间和温度等因素的影响，冷藏或冷冻食品到达消费者手中时最终品质会产生变化。为分析产品的损耗成本，这里我们引进生鲜产品损耗函数[13]：

(7)

其中,H0为产品初始质量，H(t)为产品经过t时间后剩余质量，∂指在一定的温度下生鲜产品的损耗系数，我们取值为0.05。这里我们根据研究对象和模型对公式进行完善：令产品的初始质量为从第一级节点运出的量，则产品损失的量为

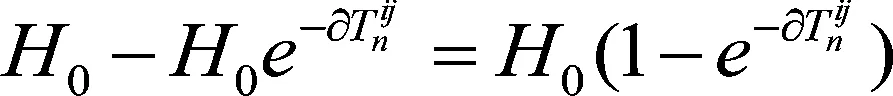
(8)

根据公式(8)可知产品损失的费用为

(9)

最终该模型为

(10)

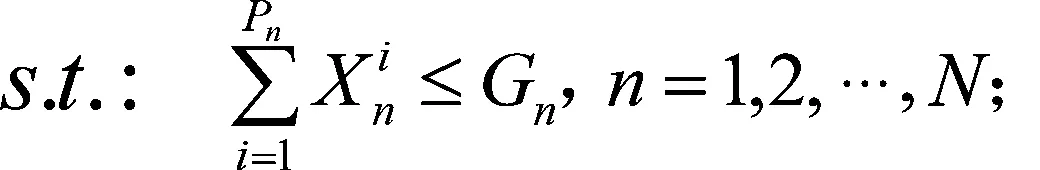
(11)

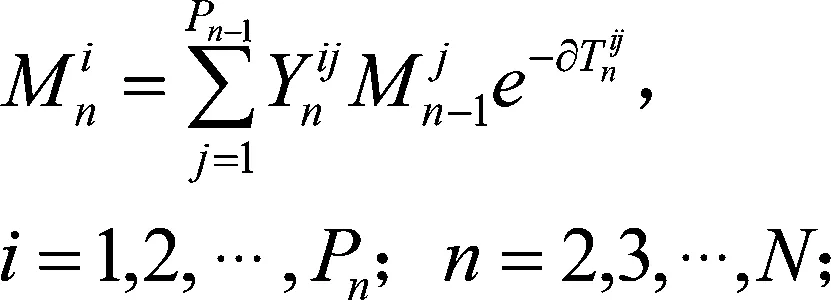
(12)

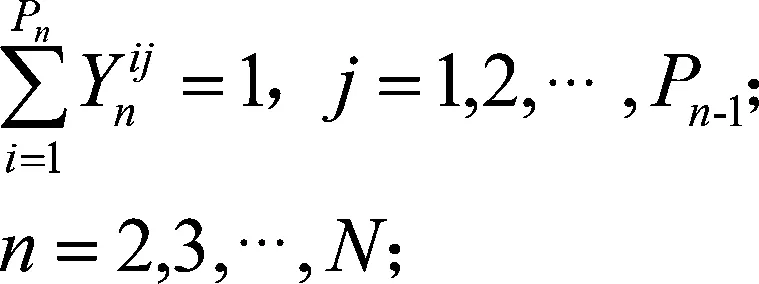
(13)

(14)

(15)

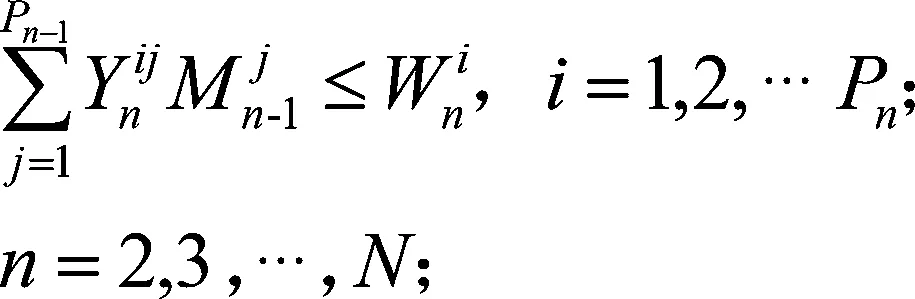
(16)

(17)

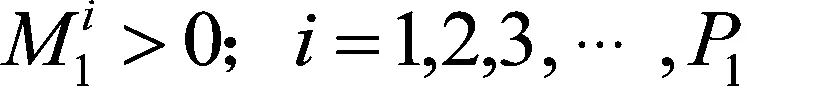
(18)

上式中，式(10)表示的是目标函数，要求目标达到总成本最低；式(11)表示被选中的物流节点数量不能超过该级拟规划建设的物流节点数量；式(12)表示除第一级物流节点外，各级物流节点的货物量由下一级物流节点运送的量决定；式(13)表示每个物流节点只能向一个上级节点发货；式(14)表示被选中的物流节点才可以发货且必须发货；式(15)表示物流节点建设后必须接收货物；式(16)表示下级物流节点向上级节点运输的货物量不得超过该上级节点的每年货物最大储存能力；式(17)表示从第二级物流节点开始每一级物流节点的总收货量等于该级物流节点需要运输的货物量；式(18)表示第一级物流节点需要运输的货物量大于0。

4 算法设计

4.1 染色体编码方案

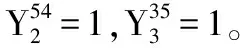
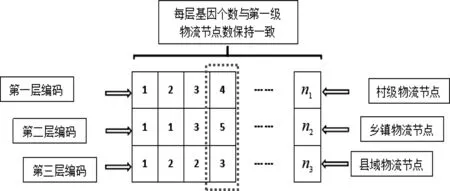
图2 染色体编码图

4.2 初始群体确定

初始种群在完成染色体编码以后通过设定种群规模参数SIZEPOP随机产生，并根据该问题存在的容量上限对各节点间的运输量进行约束产生可行解。

4.3 适应度函数设计

传统遗传算法中，适应度函数值越大，算法结果越接近最优值，因此本文定义模型目标函数的倒数作为适应度函数。

4.4 算法流程

①初始化参数：种群规模、最大迭代次数max-k、交叉概率、变异概率等；

②通过对节点容量进行判断，构造初始种群，并初始化迭代次数k=0，根据适应度函数计算初始种群的适应度值；

③根据轮盘赌法从初始种群中选出部分个体(子代1)进行交叉变异操作；

④从子代1中随机选取两个个体，设定交叉片段长度N。随机选取交叉位置，对两个个体进行片段交叉。然后通过映射原则对交叉后的两个个体进行修复，确保染色体信息正确。最后对修复后的两个个体进行容量约束的判断，满足则保留个体，形成子代2，不满足则重复此操作；

⑤对子代2中的所有个体进行变异操作，即选中一个个体，对选中的个体中的第二层和第三层染色体部分片段进行逆转操作。对逆转操作后的个体进行容量约束的判断，满足则保留，形成子代3，不满足则重复此操作；

⑥计算子代3中所有个体的适应度函数值，并与父代个体进行整合，形成下一次迭代的父代种群。迭代次数k=k+1；

⑦判断迭代次数是否大于max-k，是则进行下一步，否则转至步骤4；

⑧输出结果。

算法流程图如图3所示。

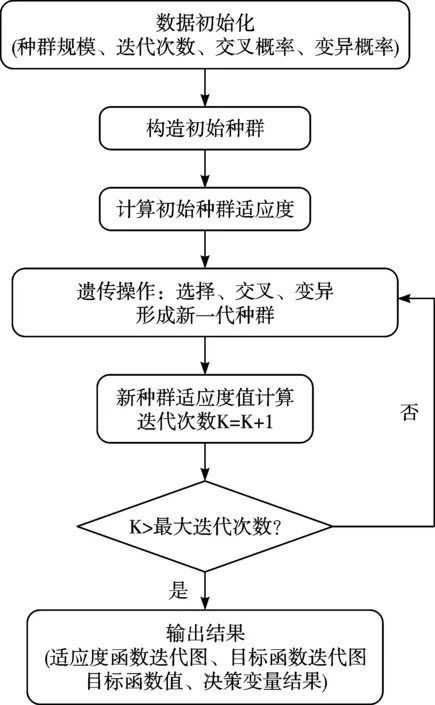
图3 算法流程图

5 算例分析

算例中，物流节点建设层级分为三层，即N=3；其中一级物流节点按照全面覆盖的原则，设为74个，该县城下辖18个乡镇(街道)，其中街道5个，乡镇13个，按照经济、交通以及基础设施等区位优势划分，二级乡镇备选物流节点为13个，三级县域备选物流节点5个。该多级物流节点系统建设规划年限为5年。拟建设的节点数量Gn(n>1)在程序运行中每次迭代时随机生成，但不超过备选节点数量，其他数据随机生成。

根据各个地点的编号以及坐标的确定，该县域多级备选物流节点分布如图4所示。

图4 多级备选物流节点分布图

在模型求解中，程序每次迭代1000次，并反复运行10次求解程序，运行结果如表1所示。

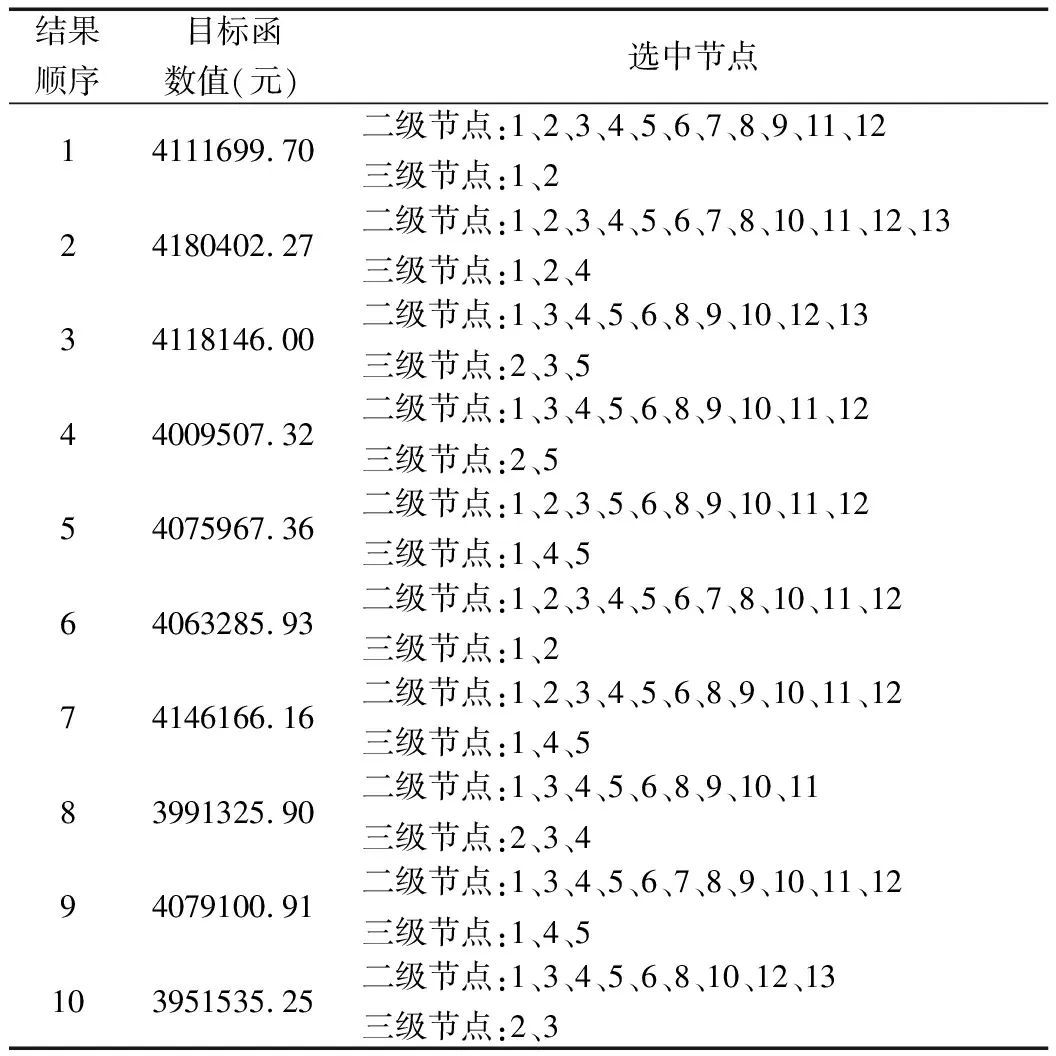
表1 算法运行结果统计表

由表1可以看出，最优解为第十次求解的结果。观察第十次算法收敛迭代图(图5)，当迭代次数超过600次时，成本的波动已基本趋平，因此可以认为迭代次数的设置在合理范围内，迭代结果具有参考意义。

图5 算法收敛迭代图

按照实际问题要求，我们求得的最低成本为3951535.25元，其中二级备选节点中选择第1、3、4、5、6、8、10、12、13个节点作为建设节点，一级备选节点选择第2、3个节点作为建设节点，与此结果对应的各节点间的运输对接情况如表2所示，优化后的多级物流节点布局如图6所示。

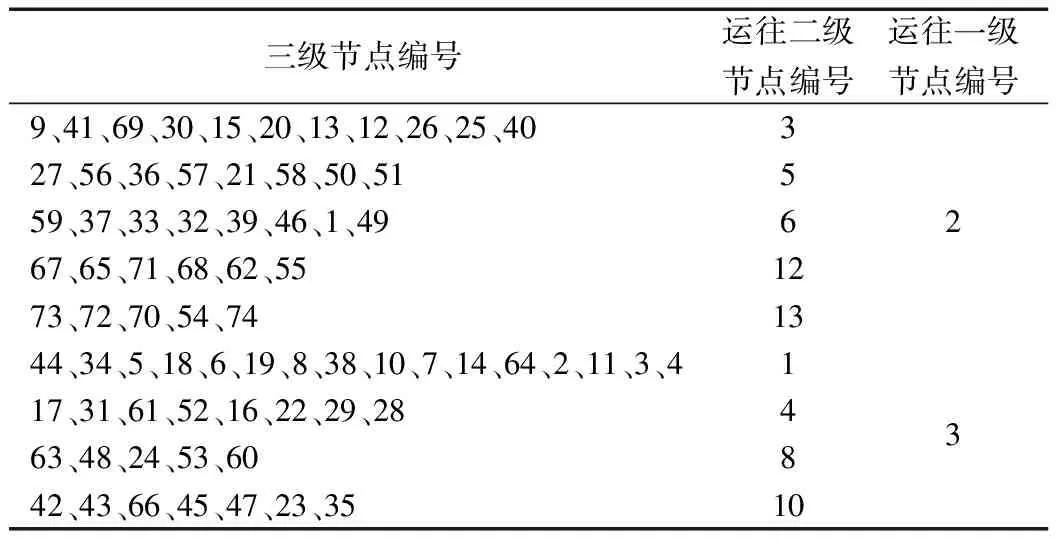
表2 各节点生鲜果蔬产品运输对接情况

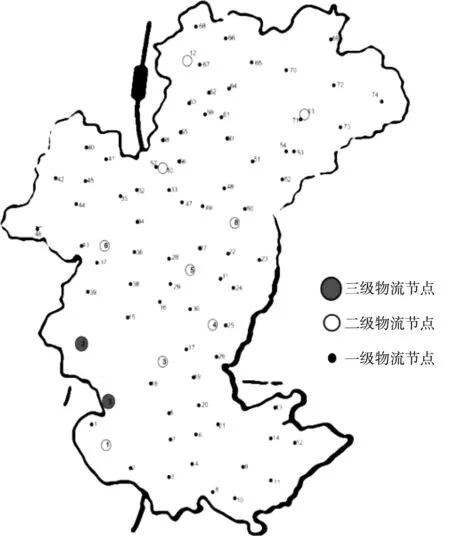
图6 优化后的多级物流节点布局图

6 结论

本文根据农村地区物流节点布局现状，将多级物流节点建设运用到农村生鲜果蔬产品“上行”至城市消费的过程中，发挥出了多级物流节点运输的高效性和服务范围的广泛覆盖性。建立了“自下而上”运输的生鲜果蔬产品物流模型，并运用遗传算法进行求解，对于广大农村地区生鲜农产品“上行”物流节点布局具有一定的指导价值和参考意义。但是本文在建模过程中，并没有考虑该多级物流节点体系在生鲜果蔬产品运输返程过程中向农村运输货物的问题。因此，如何对农村地区生鲜果蔬电商多级物流节点双向运输物流运营成本与收益作出综合评估，使该类型物流节点布局既能提高社会效益又能提高经济效益，是接下来的主要研究方向。