水下拖曳浮标系统要素匹配性分析
2022-05-12何文生邵永勇杨壮滔
张 镇, 张 涛, 何文生, 朱 敏, 邵永勇, 杨壮滔
水下拖曳浮标系统要素匹配性分析
张 镇, 张 涛, 何文生, 朱 敏, 邵永勇, 杨壮滔
(中国船舶集团有限公司 第705研究所昆明分部, 云南 昆明, 650118)
水下拖曳浮标系统是水下航行器隐蔽通信和定位的重要手段之一, 浮标、拖缆和拖带平台三要素之间的相互匹配对系统的使用至关重要。基于Ablow和Schechter提出的经典拖缆动力学分析方法, 以某水下拖曳浮标系统为研究对象, 研究分析了拖曳速度、拖带深度、浮标俯仰角等因素变化对拖缆位形和张力的影响; 以满足拖带安全性和最小化拖带负荷为目标, 建立了一种浮标、拖缆与拖带平台三要素匹配分析方法, 分析了不同工况下的最优匹配规律, 并提出了绞车及浮标相应的控制期望目标。研究结果表明: 存在浮标最优俯仰角, 使水下拖曳浮标系统满足拖带安全性、拖带负荷最小等要求, 且最优俯仰角随拖曳速度的减小、拖带深度的增大而逐渐增大。
水下拖曳浮标; 拖缆; 匹配分析
0 引言
海洋拖曳系统在海洋探测、水文调查、海上打捞救援、军事反潜以及水声对抗等领域具有重要且广泛的应用[1]。水下拖曳浮标系统主要由浮标、拖缆和拖带平台三部分组成, 是水下航行器(拖带平台)隐蔽通信和定位的重要手段。以水下航行器作为拖带平台, 通过绞车放缆释放浮标至水面或近水面。浮标升起搭载的大尺寸倒伏天线, 出水完成导航定位和通信任务。任务完成后, 浮标收起天线, 绞车收缆, 回收浮标。水下拖曳浮标系统的工作流程如图1所示。
水下拖曳浮标系统工作时, 拖曳速度、拖带深度以及浮标升阻特性影响着拖缆位形和张力, 拖缆位形及张力反过来又影响着拖带平台的拖带负荷、拖带平台及浮标的稳定控制等。另外, 从拖带平台与拖缆的安全性看, 当拖缆与拖带平台的夹角过小时, 拖缆很容易被航行器的螺旋桨吸入, 发生事故。因此, 构成水下拖曳浮标系统的浮标、拖缆和拖带平台三要素之间的相互匹配对拖曳浮标系统的使用至关重要。此外, 水下拖曳浮标系统的要素匹配性分析也是开展水下拖曳浮标系统优化设计的核心。然而, 在拖曳系统的研究方面, 国内外学者多聚焦于系统的运动预报, 未见对拖曳系统要素匹配性分析的相关研究报道[2-4]。
水下拖曳浮标系统的三要素互相耦合, 受力非常复杂。开展水下拖曳浮标系统的要素匹配性分析, 首先需要对三要素复杂的受力关系进行解耦。不难发现, 在三要素中, 浮标和拖带平台的运动均受拖缆受力影响较大, 因此, 解耦的关键是开展拖缆运动的动力学分析。
在拖缆运动的动力学分析研究中, 拖缆的数学建模方法主要有集中质量法[5]、有限差分法[6]、有限元法[7]和直接积分法[8]4种。其中Ablow和Schechter提出的有限差分法, 因在大时间步长的仿真中具有较好的稳定性而得到了广泛的应用[9]。国内外学者采用该方法对水面船拖曳线列阵和水下拖体、水下航行器拖曳线列阵和浮标的拖缆运动开展了大量研究, 能够准确地预报拖缆位形和张力[10-15]。
文中以某水下拖曳浮标系统为研究对象, 采用Ablow和Schechter提出的经典拖缆动力学分析方法, 研究分析拖曳速度、拖带深度、浮标俯仰角的变化对拖缆位形和张力的影响; 以满足拖带安全性和拖带负荷最小化为目标, 建立浮标、拖缆与拖带平台三要素匹配分析方法, 分析不同工况下的要素最优匹配规律, 为绞车和浮标使用提出相应的控制期望目标。
1 拖缆动力学分析方法及验证
1.1 拖缆动力学分析方法
在Ablow和Schechter方法中, 拖缆动力学方程写成矩阵形式为
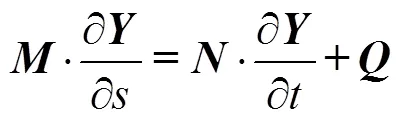
拖缆动力学方程是非线性的偏微分方程, 无法得到解析解, 采用有限差分法对其进行空间和时间离散, 即

拖缆首端与拖带平台相连, 首端点速度与拖带平台速度相等; 拖缆尾端与浮标相连, 尾端张力使浮标处于平衡状态。由此可建立拖缆首端和尾端边界条件, 使方程组封闭。
联立拖缆首端和尾端边界条件, 对离散方程组采用牛顿迭代法进行数值求解, 即可得到拖缆运动的计算结果。求解流程如图2所示。
1.2 试验验证
为验证求解算法的准确性, 采用Rispin[16]海上水面船拖曳线列阵试验数据进行验证, 如图3所示。该试验中, 水面船分别以10 kn、18.5 kn航速拖曳线列阵直航, 线列阵的相关参数如表1所示。仿真结果与试验数据的对比如表2所示, 仿真得到的拖缆位形如图4所示。
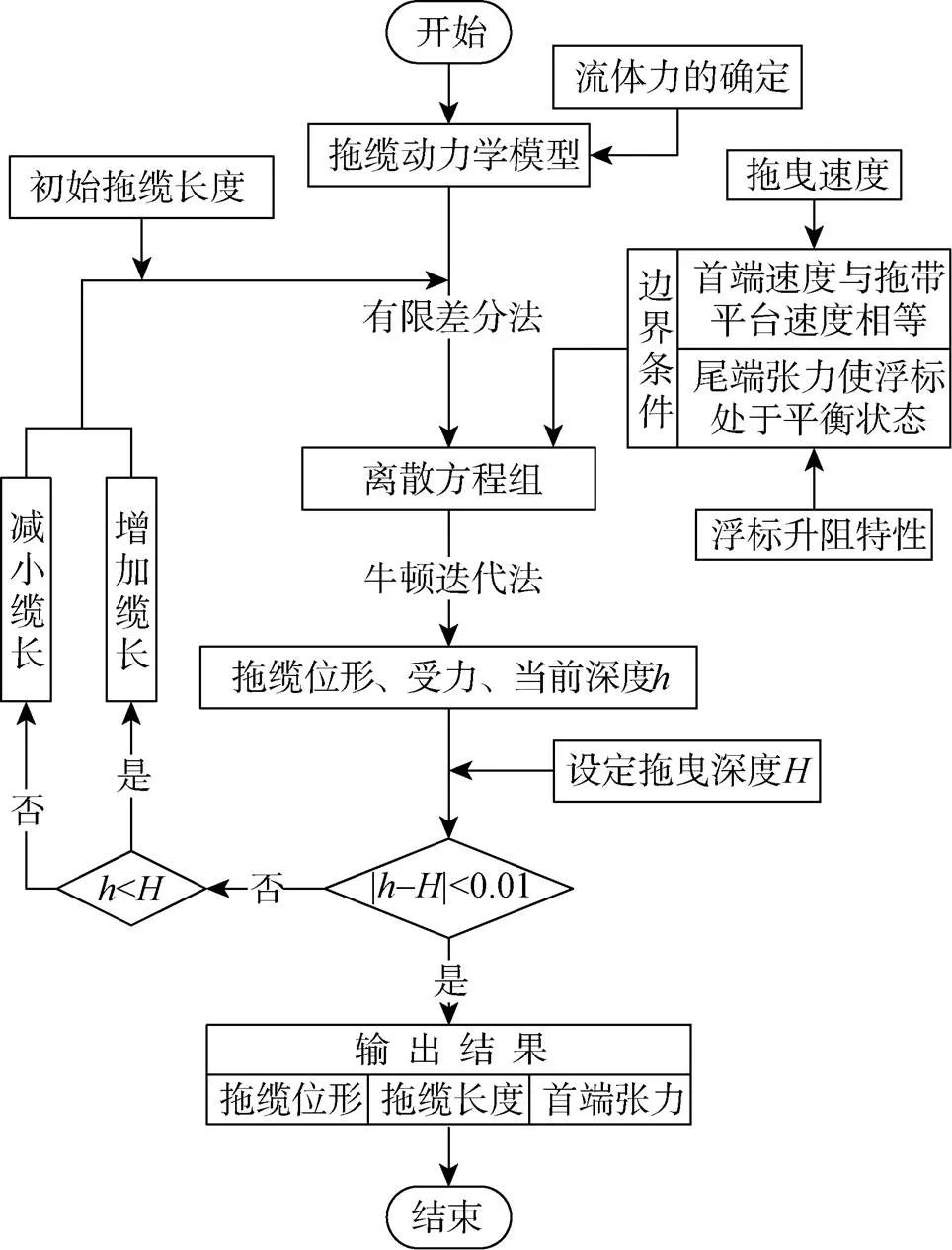
图2 求解流程图
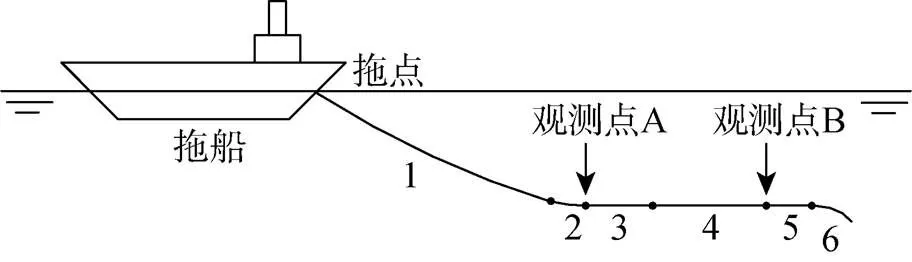
图3 拖曳线列阵示意图

表1 拖缆各组成部分物理参数
注:和分别为拖缆切向阻力系数和法向阻力系数。
通过对比发现, 仿真结果与试验数据吻合较好, 拖缆纵倾角的误差为3.70%, 观测点深度误差在1%以内, 计算精度较高。因此, 采用该求解算法是合理准确的。

表2 仿真结果与试验结果对比

图4 10 kn和18.5 kn拖曳速度下的缆形
2 研究对象及输入条件

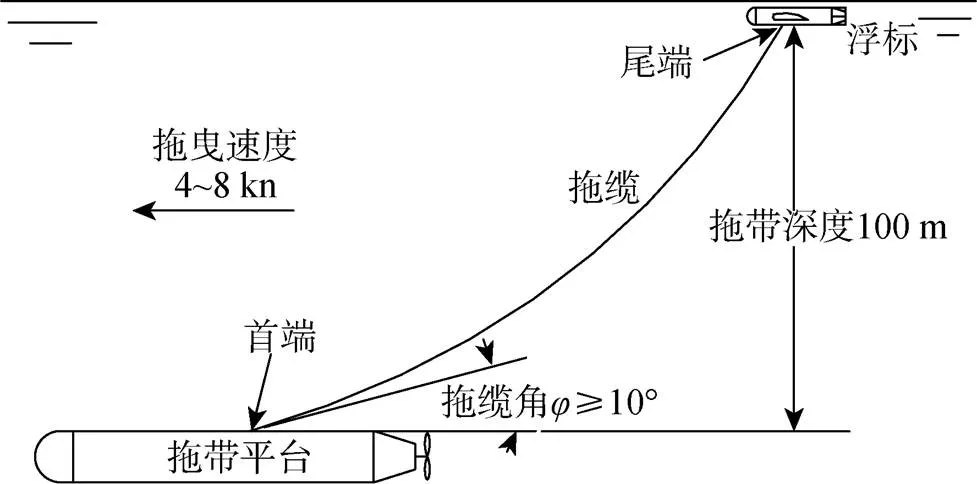
图5 水下拖曳浮标系统示意图
2.1 浮标升阻特性
浮标与拖缆尾端相连, 其升阻特性是拖缆动力学分析计算的重要输入条件。文中研究的浮标采用升力体设计, 外形结构如图6所示, 浮标主翼产生升力, 抵消拖缆的下拽力, 尾部有“X”型全动舵, 能够自主调节浮标的俯仰角。

图6 浮标外形图

该浮标的升阻特性如图7所示。

图7 浮标升阻特性曲线
2.2 拖缆参数
拖缆本身的物理参数也是拖缆动力学分析计算重要的输入条件, 具体参数如表3所示。
在额定拉力下, 拖缆直径的变化仅有0.15%, 对拖缆受力和位形影响很小[17], 拖缆计算中, 忽略拖缆受拉后直径变化的影响。

表3 拖缆物理参数
3 拖缆动力学特性影响因素分析
以图5所示水下拖曳浮标系统为研究对象, 根据给定的输入条件, 研究分析拖曳速度、拖带深度、浮标俯仰角等因素对拖缆动力学特性的影响。
3.1 拖曳速度
拖带平台以航速4~8 kn、深度100 m直航拖曳浮标, 浮标俯仰角稳定在5°, 拖缆直径13 mm。仿真计算的拖缆位形和张力结果如表4、图8和图9所示。

表4 不同拖曳速度的拖缆计算结果
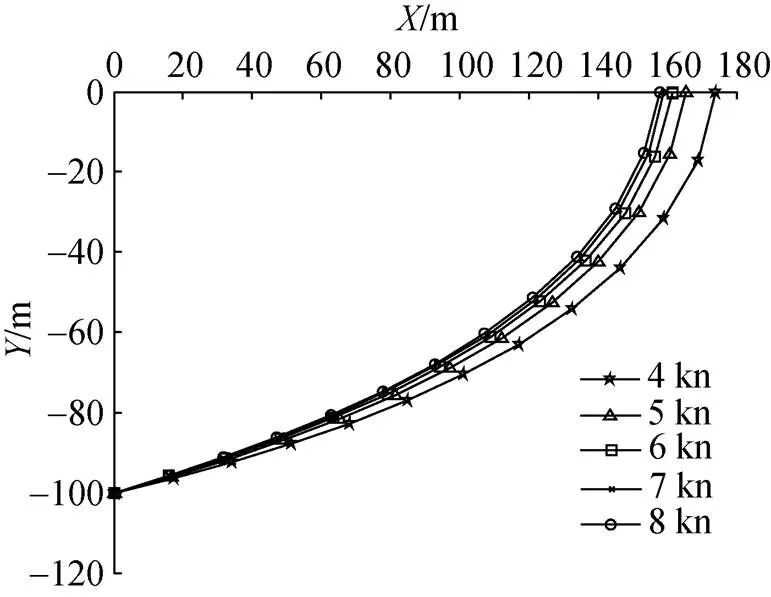
图8 不同拖曳速度下的拖缆位形

图9 不同拖曳速度下的拖缆张力分布
对比可知, 不同拖曳速度下, 拖缆位形均呈抛物状, 拖缆张力分布趋势相同: 从拖缆首端至尾端, 缆上张力逐渐减小; 当拖曳速度增大时, 拖缆角随之增加, 维持拖带深度所需拖缆长度逐渐变短, 拖缆首端张力逐渐增大。
由表4可见, 4~8 kn拖曳速度范围内, 以5°俯仰角拖曳浮标, 拖缆位形均满足拖缆角不小于10°的使用要求。
3.2 拖带深度
拖带平台以航速6 kn、深度80~120 m直航拖曳浮标, 浮标俯仰角稳定在5°。仿真计算的拖缆位形和张力结果如表5、图10和图11所示。

表5 不同拖带深度的拖缆计算结果

图10 不同拖带深度下的拖缆位形

图11 不同拖带深度下的拖缆张力分布
由表5、图10和图11可见, 不同拖带深度下, 拖缆位形均呈抛物状, 拖缆张力分布趋势相同; 当拖带深度逐渐增大时, 拖缆角随之减小, 维持拖带深度所需拖缆长度和拖缆首端张力逐渐增大。
3.3 浮标俯仰角
拖带平台以航速6 kn、深度100 m直航拖曳浮标, 浮标俯仰角取1°~5°范围。仿真计算的拖缆位形和张力结果如表6、图12和图13所示。
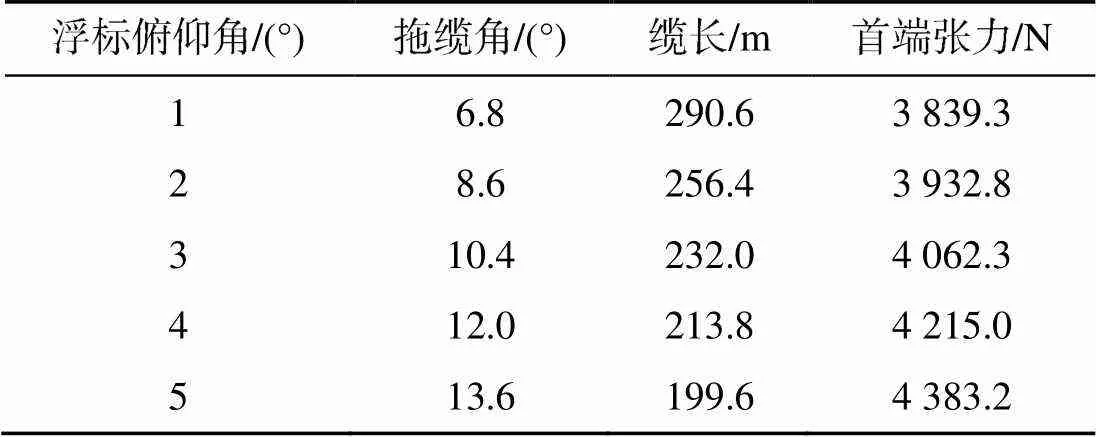
表6 不同浮标俯仰角的拖缆计算结果

图12 不同俯仰角下的拖缆位形

图13 不同俯仰角下的拖缆张力分布
由表6、图12和图13可见, 不同俯仰角下, 拖缆位形均呈抛物状, 拖缆张力分布趋势相同; 当浮标俯仰角增大时, 拖缆角随之增加, 维持拖带深度所需拖缆长度逐渐变短, 拖缆首端张力逐渐增大。从表6还可以看出, 浮标俯仰角必须大于2°, 才能满足拖缆角不小于10°的要求。
4 匹配性分析
在拖曳速度、拖带深度和浮标俯仰角3个参数中, 前两者由工作海域环境与实际任务决定, 浮标俯仰角则能够通过操舵实现自主控制。因此, 对不同的拖曳工况, 可以采用调节浮标俯仰角并配合收放拖缆的方式, 达到满足拖带安全性且拖带平台拖带负荷最小的拖曳状态。
结合俯仰角对拖缆角的影响规律, 建立浮标、拖缆和拖带平台3要素匹配分析流程如图14所示。对确定的水下拖曳浮标系统, 根据给定的拖曳速度和拖带深度, 通过迭代求解浮标俯仰角, 达到既满足拖缆使用安全性即拖缆角不小于10°, 又实现拖带平台拖带负荷最小的最优匹配目标, 得到该工况下浮标、拖缆和拖带平台的最优匹配关系。

图14 匹配性分析流程图
通过对不同拖曳速度、拖带深度等拖曳工况开展匹配分析, 可以得到不同工况下的最优匹配结果。将这些结果按变工况次序连接, 可以得到变工况下的要素最优匹配曲线。
4.1 变速工况
对拖带平台航速4~8 kn、拖带深度100 m直航拖曳浮标的设计工况进行匹配分析, 得到不同拖曳速度下, 浮标、拖缆和拖带平台的最优匹配关系如表7所示。
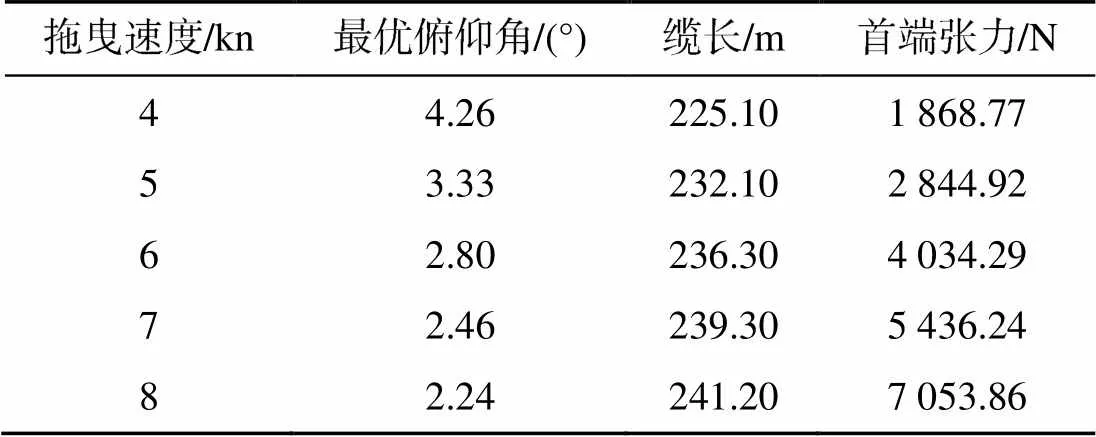
表7 不同拖曳速度工况的匹配最优解
由表7可见, 在拖缆角不小于10°及拖带平台负荷最小约束条件下, 不同拖曳速度下存在不同的最优俯仰角, 当拖曳速度逐渐增大时, 最优俯仰角逐步减小、所需拖缆长度逐步增加。
4.2 变深工况
对拖带平台航速6 kn、拖带深度80~120 m直航拖曳浮标的工况进行匹配分析, 得到不同拖带深度下, 浮标、拖缆和拖带平台的最优匹配关系如表8所示。
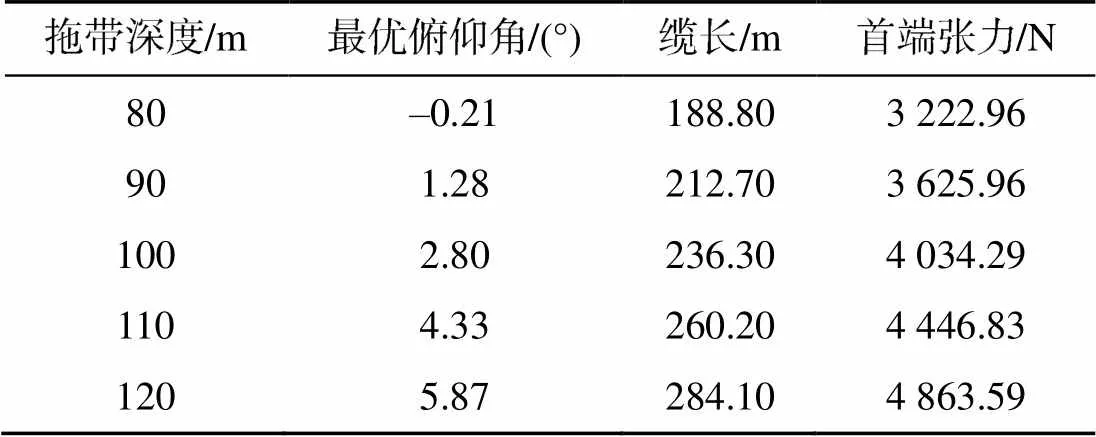
表8 不同拖带深度工况的匹配最优解
由表8可见, 在拖缆角不小于10°及拖带平台负荷最小约束条件下, 不同拖带深度下存在不同的最优俯仰角, 当拖带深度逐渐增大时, 最优俯仰角逐步增大、所需拖缆长度逐步增加。
4.3 变速变深工况
对拖带平台航速4~8 kn、拖带深度80~100 m直航拖曳浮标的工况进行匹配分析, 得到不同拖曳速度和拖带深度下, 浮标、拖缆和拖带平台的最优匹配关系如图15~图17所示。
由图可见, 不同拖曳速度、拖带深度下的匹配优化结果呈空间曲面分布。当拖曳工况由逐渐变为时,按其在图15和图16所示空间曲面上的投影曲线变化规律调节浮标俯仰角和拖缆长度, 即可实现在对应工况变化下, 满足拖缆角不小于10°的安全性要求, 且拖带平台的拖带负荷最小。图17对应的首端张力变化则能够作为拖带平台稳定控制的输入, 为拖带平台的变速变深稳定控制提供数据支撑。
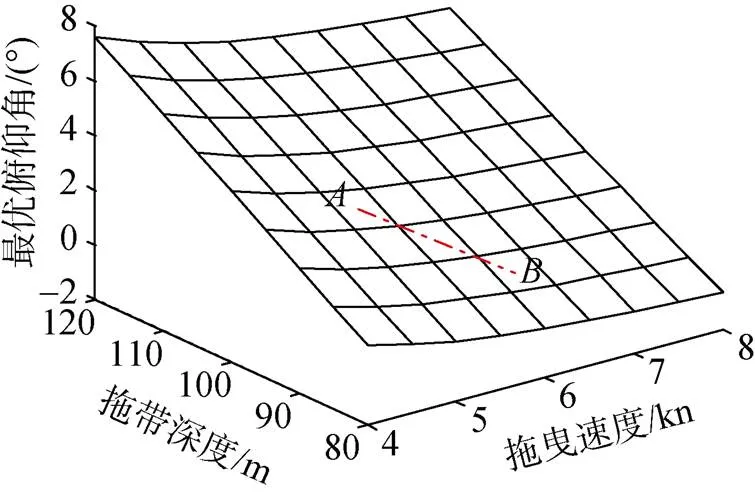
图15 不同拖曳速度和拖带深度下的最优俯仰角

图4 最优俯仰角对应的拖缆长度

图17 最优俯仰角对应的拖缆首端张力
将最优浮标俯仰角及对应的拖缆长度和首端张力随拖曳速度和拖带深度变化的规律拟合成空间曲面数学关系式, 即

由式(4)可见, 最优俯仰角、所需拖缆长度以及拖缆首端张力均与拖曳速度成平方关系, 与拖带深度成线性关系。将式(4)所示规律写入浮标舵控制指令、绞车缆长控制程序以及拖带平台稳定控制算法中, 可实现使水下拖曳浮标系统满足安全性的同时, 拖带平台拖带负荷最小的精准自动控制。
5 结论
文中采用Ablow和Schechter提出的经典拖缆动力学分析方法, 以某水下拖曳浮标系统为研究对象, 研究分析了拖曳速度、拖带深度、浮标俯仰角等因素变化对拖缆位形和张力的影响, 并以满足拖带安全性和最小化拖带平台拖带负荷为目标, 建立了一种浮标、拖缆与拖带平台三要素匹配分析方法, 分析了不同工况下的要素最优匹配规律, 并对绞车及浮标提出了相应的控制期望目标, 具体结论如下。
1) 不同拖曳速度、拖带深度、浮标俯仰角的工况下, 拖缆位形均呈抛物状, 拖缆张力分布趋势相同: 首端张力最大, 从首端至尾端逐渐减小;
2) 随着拖曳速度的增大、拖带深度的减小、浮标俯仰角的增大, 拖缆角逐渐增大, 所需的拖缆长度逐渐变短; 随着拖曳速度、拖带深度、浮标俯仰角的增大, 拖缆首端张力逐渐增大;
3) 不同拖曳工况下, 使拖曳系统在满足拖带安全性、拖带平台负荷最小的最优匹配结果呈现不同的规律: 当拖曳速度逐渐增大时, 最优俯仰角逐渐减小, 所需的拖缆长度逐渐增大; 当拖带深度逐渐增大时, 最优俯仰角和所需的拖缆长度都逐渐增大;
4) 基于优化匹配结果, 得到最优俯仰角及对应拖缆长度和首端张力与拖带深度、拖曳速度的函数关系, 提出了绞车和浮标的控制期望目标。
文中建立的匹配分析方法和得到的规律性成果对水下拖曳浮标系统优化设计具有现实的指导意义。需要指出的是, 该结果是在忽略风、浪及洋流等环境影响下得到的, 后续研究工作应将环境因素对水下拖曳浮标系统的影响考虑在内。
[1] 叶果洛夫. 水下拖曳系统[M]. 北京: 海洋出版社, 1989.
[2] 苑志江, 金良安, 田恒斗, 等. 海洋拖曳系统的水动力理论与控制技术研究综述[J]. 科学技术与工程, 2013, 13(2): 408-415, 420.
Yuan Zhi-jiang, Jin Liang-an, Tian Heng-dou, et al. Comments on the Research of Hydrodynamic and Control Technology of Underwater Towed System[J]. Science Technology and Engineering, 2013, 13(2): 408-415, 420.
[3] 庞师坤, 刘旌扬, 王健, 等. 二级深拖系统的回转运动特性[J]. 船舶工程, 2017, 39(9): 71-77.
Pang Shi-kun, Liu Jing-yang, Wang Jian, et al. Motion Characteristics of Two-part Towed System during Towing Ship Turning Maneuvers[J]. Ship Engineering, 2017, 39(9): 71-77.
[4] 敖雷, 连琏, 徐雪松, 等. 母船垂荡运动下拖缆响应研究[J]. 船舶工程, 2013, 35(z1): 28-31, 51.
Ao Lei, Lian Lian, Xu Xue-song, et al. Study of Towed Cables Response under Heave Motion of Mother Ships[J]. Ship Engineering, 2013, 35(z1): 28-31, 51.
[5] Walton T S, Polachek H. Calculation of Transient Motion of Submerged Cables[J]. Mathematics of Computation, 1960, 14(69): 27-46.
[6] Ablow C M, Schechter S. Numerical Simulation of Undersea Cable Dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457.
[7] Leonard J W, Nath J H. Comparison of Finite Element and Lumped Parameter Methods for Oceanic Cables[J]. Engineering Structures, 1981, 3(3): 153-167.
[8] Sun Y, Leonard J W, Chiou R B. Simulation of Unsteady Oceanic Cable Deployment by Direct Integration with Suppression[J]. Ocean Engineering, 1994, 21(3): 243-256.
[9] 吴家鸣, 郁苗, 朱琳琳. 带缆遥控水下机器人水动力数学模型及其回转运动分析[J]. 船舶力学, 2011, 15(8): 827-836.
Wu Jia-ming, Yu Miao, Zhu Lin-lin. A Hydrodynamic Model for a Tethered Underwater Robot and Dynamic Analysis of the Robot in Turning Motion[J]. Journal of Ship Mechanics, 2011, 15(8): 827-836.
[10] Wu J, Chwang A T. A Hydrodynamic Model of a Two-part Underwater Towed System[J]. Ocean Engineering, 2000, 27(5): 455-472.
[11] 马伟, 师子锋. 收放拖缆对拖体深度影响的仿真分析[J]. 水雷战与舰船防护, 2012(3): 67-69.
Ma Wei, Shi Zi-feng. Simulation Analysis on Effects of Deploying and Retracting Cable to Towed Body Depth[J]. Mine Warfare & Ship Self-Defence, 2012(3): 67-69.
[12] 叶凡滔, 陈彦勇, 邵永勇, 等. 一种水下非均质拖曳线列阵动力学仿真方法及试验验证[J]. 舰船科学技术, 2017, 39(3): 127-130, 134.
Ye Fan-tao, Chen Yan-yong, Shao Yong-yong, et al. A Dynamic Simulation Method and Experimental Verification of Underwater Heterogeneous Towed Linear Array[J]. Ship Science and Technology, 2017, 39(3): 127-130, 134.
[13] 张大朋, 白勇, 章浩燕, 等. 海洋缆索对水下航行器的动态响应[J]. 水道港口, 2019, 49(5): 600-605.
Zhang Da-peng, Bai Yong, Zhang Hao-yan, et al. Dynamic Response of Marine Cable for the Underwater Vehicle[J]. Journal of Waterway and Harbor, 2019, 49(5): 600-605.
[14] 杜晓旭, 宋保维, 潘光. 拖曳式导航浮标对回转体UUV操纵性的影响[J]. 兵工学报, 2010, 31(9): 1164-1168.
Du Xiao-xu, Song Bao-wei, Pan Guang. Effects of Dragging Navigation Buoyage on Maneuverability of Body-of-revolution UUV[J]. Acta Armamentarii, 2010, 31(9): 1164-1168.
[15] 杜晓旭, 宋保维, 潘光. 水下双拖系统动力学建模与仿真[J]. 西北工业大学学报, 2011, 29(1): 82-86.
Du Xiao-xu, Song Bao-wei, Pan Guang. A New Method for Calculating a Two-Part Underwater Towed System[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 82-86.
[16] Rispin P. Data Package No.1 for Cable and Array Maneuvering[R]. Bethesda, MD, US: Naval Ship Research and Development Center, 1980.
[17] 王飞, 黄国樑, 邓德衡. 水下拖曳系统的稳态运动分析与设计[J]. 上海交通大学学报, 2008, 42(4): 679-684.
Wang Fei, Huang Guo-liang, Deng De-heng. The Design and Steady-State Simulation of Underwater Towed System[J]. Journal of Shanghai Jiao Tong University, 2008, 42(4): 679-684.
Element Matching Analysis Method for Underwater Towed Buoy Systems
ZHANG Zhen, ZHANG Tao, HE Wen-sheng, ZHU Min, SHAO Yong-yong, YANG Zhuang-tao
(Kunming Branch of the 705 Research Institute, China State Shipbuilding Corporation Limited, Kunming 650032, China)
An underwater towed buoy system is an important means of undersea vehicle concealed communication and positioning. To utilize this system, it is crucial to match the buoy, tow cable, and towed vehicle. In this study, based on the classical method proposed by Ablow and Schechter for analyzing towed cable dynamics, we investigated the influence of towing velocity, towing vehicle depth, and buoy’s pitch angle on the tow cable’s shape and tension, considering an underwater towed buoy system as the research object. To meet the requirements of towing security and minimize the towing vehicle load, we established an analysis method for matching the buoy, tow cable, and towing vehicle, obtained the optimal matching law under different working conditions, and proposed the corresponding control expectation target of the winch and buoy. The results demonstrate that the buoy optimal pitch angle, which ensures that the underwater towed system fulfils the towing safety and minimum towing load requirements, increases with decreasing towing velocity and increasing towing depth.
underwater towed buoy; towed cable; matching analysis
张镇, 张涛, 何文生, 等. 水下拖曳浮标系统要素匹配性分析[J]. 水下无人系统学报, 2022, 30(2): 170-177.
U674.941; TJ630.2
A
2096-3920(2022)02-0170-08
10.11993/j.issn.2096-3920.2022.02.005
2022-01-01;
2022-01-11.
张 镇(1998-), 男, 在读硕士, 主要研究方向为水下航行器总体技术.
(责任编辑: 许 妍)
