一种求解无线传感器网络定位问题的改进状态转移算法
2022-05-11王小荣李建军
王小荣 彭 炫 李建军 张 海
(新疆大学工程训练中心,新疆 乌鲁木齐 830047)
1 概述
传感器网络定位(SNL)问题广泛应用于无线传感器网络的控制和监测中,如在给定的无线电范围内收集环境数据(温度、振动运动、湿度),以及库存管理等[1]。无线传感器网络是一组分布在一定地理区域的传感器,网络中传感器的准确位置是影响应用效率的关键。具体来说,对于一个有n 个无线传感器的网络,SNL 问题是在给定一些传感器对之间的距离和ma个已知传感器(称为锚)的精确位置的条件下,估计m 个未知传感器的位置,其中n=m+ma,m≻ma。需要注意的是,锚的位置可以通过全球定位系统(GPS)或在部署过程中的人工处理来获得,但其代价昂贵,而且有物理条件的限制,因此锚的数量很少。目前的大多数研究是通过最小二乘法将SNL问题转化为一个非凸优化问题来求解[2]。要准确定位未知传感器,主要有三个难点:第一,距离测量可能包含噪声。第二,很难找到SNL 问题的充分条件。第三,已经证明SNL 问题是NP-hard 问题[3]。在过去的十年中,人们提出了许多基于梯度的方法来近似求解SNL 问题。其中,半定规划(SDP)松弛法往往不能准确地得到SNL 问题的最优解[4]。因此,由SDP 方法得到的解通常四舍五入为次最优解。由于距离测量可能包含某种噪声,因此SDP 得到的次优解不可靠且鲁棒性较差。与SDP 松弛相比,二阶锥规划(SOCP)松弛法得到的解略差,但结构简单,消耗时间短,常被用作SNL 问题的预处理[5]。另一方面,据我们所知,虽然元启发式算法在近几十年发展迅速,一些随机优化方法也被应用于SNL 问题,但其效果并不理想。例如粒子群优化算法解决SNL 问题时,传感器的数量限制在100 个以内[6]。值得一提的是,文献[2]采用了一种动态转移算法来解决SNL 问题。虽然能够解决100 个以上传感器的SNL 问题,但鲁棒性较差,解决大规模的SNL 问题耗时较长。状态转移算法是近年来提出的一种随机优化方法[7]。不同于许多基于种群的元启发式算法,如遗传算法、粒子群算法、蚁群算法,它是一种基于个体的搜索技术。由于STA 搜索能力强大,易于实现,其已被广泛应用于许多工程领域,如风电功率预测[8]、图像分割[9]、混沌系统参数辨识[10]等。虽然STA 在解决许多优化问题方面具有很好的表现,但其仍存在一些不足[11]。例如,在求解某些复杂基准函数时,基本STA 求解精度低,收敛速度慢。在解决大规模SNL 问题时,鲁棒性较差,甚至无法得到可行解。鉴于基本STA 的不足,本文提出了一种改进的状态转移算法。首先采用统计方法对STA 的参数进行选择。然后采用二次插值技术增强其局部开发能力,提高求解精度。此外,为了减小算法陷入局部最优解的概率,设计了一种新的变异策略来提高全局探索性能。最后采用基于梯度的方法对算法进行加强,并成功地应用于300 个传感器的大规模SNL 问题。
2 基本状态转移算法
状态转移算法(STA)是一种基于状态空间和状态转移概念的随机优化方法。一般来说,在基本STA 中,生成候选解的统一形式定义如下[12]:

2.1 状态变换算子
在标准STA 中,通过参考各种类型的状态空间变换,使用四个智能算子来解决连续优化问题。
2.1.1 旋转变换

2.2 规则邻域及采样技术
不难理解,对于一个特定的解,理论上可以使用某种状态变换算子生成无限多个候选解,从而形成一个规则邻域。显然,列出所有候选解决方案是不实际的,考虑到STA 中每个算子的状态转移矩阵是随机生成的,算子生成的候选解也是随机的,不是唯一的,且任何两个解都相互独立。在此基础上,将生成的候选解视为样本,通过选取具有代表性的样本来反映邻域的整体特征。例如,在伸缩变换中,独立执行扩展运算符SE 次,其伪代码如下:
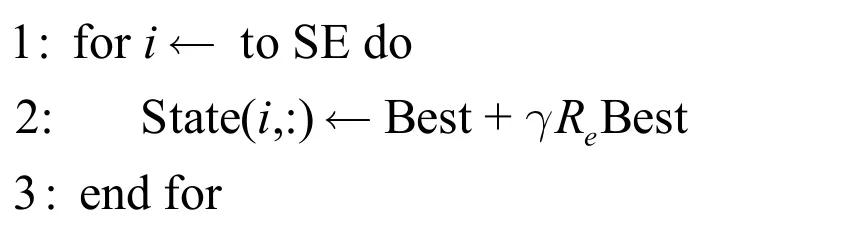
其中,SE 为搜索强制,表示伸缩变换生成的样本数;Best 为当前最好解。
3 改进状态转移算法
本小节提出了一种改进的状态转移算法(ISTA)。在ISTA 中,采用统计方法优化状态变换算子因子的选择[13],然后采用二次插值技术代替平移变换算子,并提出了一种新的随机变异策略,以提高算法跳出局部最优解的概率。下面将详细介绍这些修改策略。
3.1 最优参数选择

3.2 二次插值策略
虽然STA 具有很强的搜索性能,在许多工程领域得到了广泛的应用,但在某些问题上仍然存在收敛速度慢的缺点。例如,在求解一些基准函数时,如Rosenbrock 函数,基本STA 在后期收敛缓慢,这也是许多启发式算法的一种现象。此外,研究发现平移变换算子的局部搜索能力不是很强,而二次插值[14](QI)方法具有很强的局部搜索能力。因此,采用QI 方法代替平移变换算子来增强STA 的局部搜索能力。QI 生成候选解的公式如下:

3.3 随机变异策略

3.4 所提算法的操作流程
通过以上讨论和分析,ISTA 算法的完整步骤描述如下:
步骤1 初始化算法参数;
步骤2 通过统计方法选择最优伸缩变换算子参数;
步骤3 执行伸缩变换,若伸缩变换产生的最好解优于当前解,以50%的概率选择执行二次插值或随机变异操作,并以贪婪准则更新当前最好解;
步骤4 重复步骤3,Tp次;
步骤5 重复步骤2,3 和4。不同的是将伸缩变换替换为旋转变换;
步骤6 重复步骤2,3 和4。不同的是将伸缩变换替换为坐标变换;
步骤7 直到满足迭代的终止条件,迭代完成,输出最优值。
为了形象的表达ISTA 算法的步骤,图1 给出了ISTA 的流程图,其中A,B,C 模块分比执行Tp次。
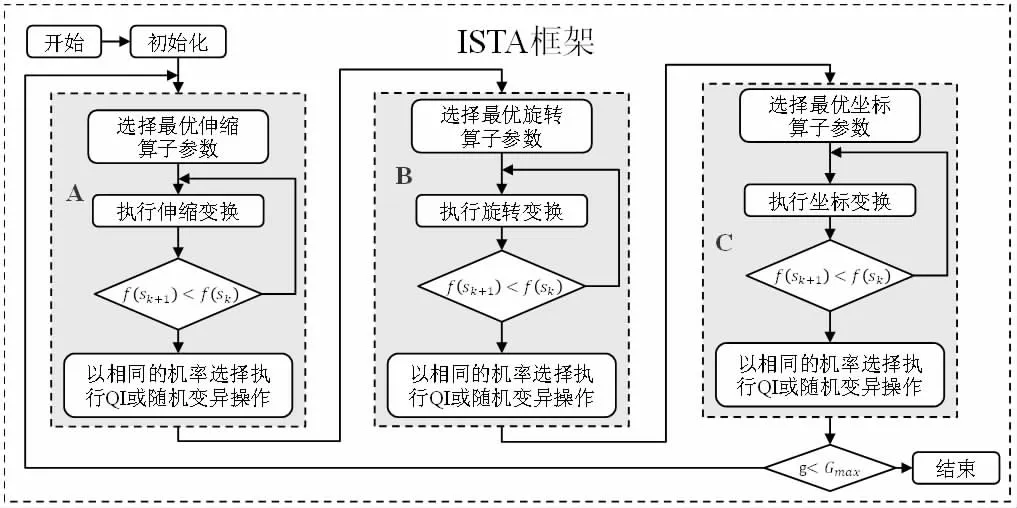
图1 ISTA 流程图
4 应用于传感器网络定位问题
4.1 ISTA 算法测试


实验中采用的4 个基准函数的理论最优值均为0。从表1 中的统计结果可以观察到,相比于基本STA 以及两种STA 的变体,ISTA 在4 个测试函数上都获得了最好的平均值和标准差。特别是对于山谷型函数Rosenbrock,ISTA 可以获得不错的精度解,这表明二次插值技术可以增强STA 的局部开发能力,加快搜索速度,使得算法快速收敛。另外,对于多峰函数Pathological,STA,DSTA 和POSTA 都陷入了局部最优解,但ISTA 也可以获得全局最优解,这表明随机变异策略可以增强算法的全局探索能力。从ISTA,HHO 和SMA 的对比结果可以看出,3 种算法除了在函数Pathological 上获得了相同结果以外,ISTA 在其他的三个测试函数上均获得了最好的结果。从图2 中几种算法的平均迭代曲线也可以形象地看出,ISTA 收敛速度快于其他5 种对比算法,且获得了更高的精度解,这证明所提算法在求解效率以及寻优精度方面均具有明显优势。

表1 几种算法在四个基准函数上的结果
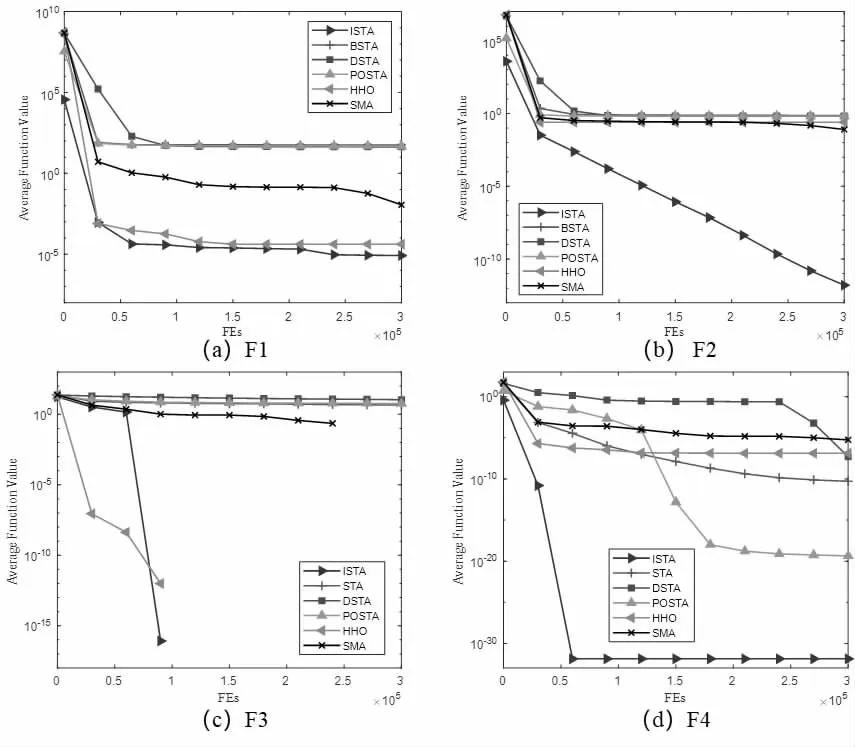
图2 几种算法的平均迭代曲线图
4.2 应用于SNL 问题

显然,由于非凸优化问题存在局部最优解,而STA 具有良好的全局搜索能力,为了进一步加强算法后期的搜索效率使其更适合求解SNL 问题,本文采用基于梯度的技术对ISTA 进行加强以提高其搜索效率,并将其应用于大规模SNL 问题的求解。
传感器实例由SFSDF[17]随机创建,它是一个用于解决SNL 问题的MATLAB 软件包。本研究创建了3 个具有4 个锚点a= (0,0),a= (0,1),a= (1,0),a=(1,1)的SNL实例,传感器均产生在区间[0,1]范围内。第一个实例有12 个传感器,无线电范围设置为1,无噪声添加。另外两个都是大规模的SNL 问题,分别有100 和300 个传感器,使用的无线电范围是0.3,噪声系数是0.001。在解决12 个传感器的SNL 问题时,ISTA 不使用基于梯度的方法进行强化,实验结果与标准STA 和DSTA 进行了比较。所有算法的最大评价函数设置为1e5,搜索范围设置为[0,10],其他参数设置与数值实验中的相同。但在解决大规模的SNL 问题时,采用了基于梯度的优化技术来提高算法的搜索效率。所有算法独立运行20 次,3 个SNL实例的实验结果见表2 和图3-6。
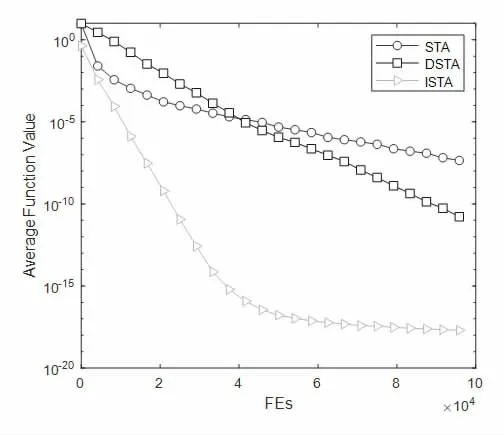
图3 三种不同算法在12 个传感器上的平均迭代曲线
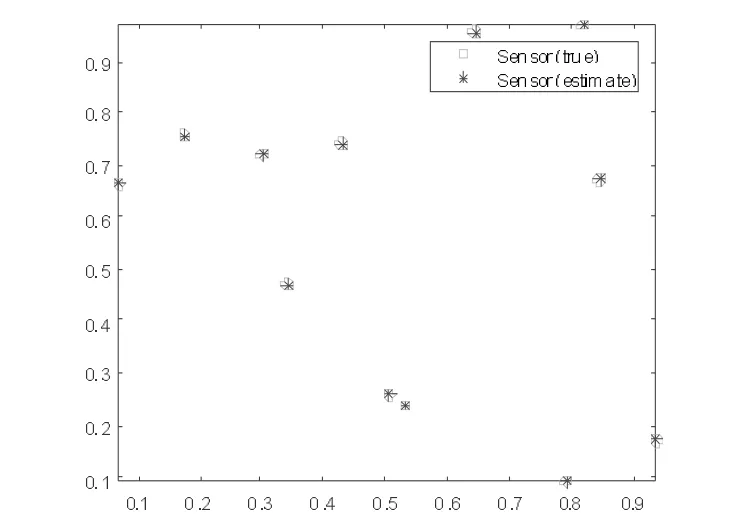
图4 STA 在300 个传感器的SNL 问题上获得的最好结果

图5 STA, DSTA and ISTA 在100 个传感器的SNL 问题上获得的最好结果

图6 STA, DSTA and ISTA 在300 个传感器的SNL 问题上获得的最好结果
更具体地说,对于12 个传感器问题,三种算法都找到了最优解。从表2 中可以看出,ISTA 得到的统计结果显示,基本STA 消耗的时间最少,但ISTA 获得的最好值、平均值、最差值和标准差均为最佳。此外,从图2 中的平均迭代曲线可以明显看出,ISTA 相比于基本STA 和DSTA 可以更快地收敛到全局最优解。此外,对于两个大规模的SNL 问题,使用基于梯度的优化技术对这三种算法都进行了进一步加强。表2 中的统计结果表明ISTA的获得的结果也是最好的,而STA 和DSTA 都陷入局部最优解,这在图5 和图6 中也得到了验证。值得强调的是,在300 个传感器的大规模SNL 问题求解中,ISTA 比基本STA 和DSTA 消耗的时间少得多。
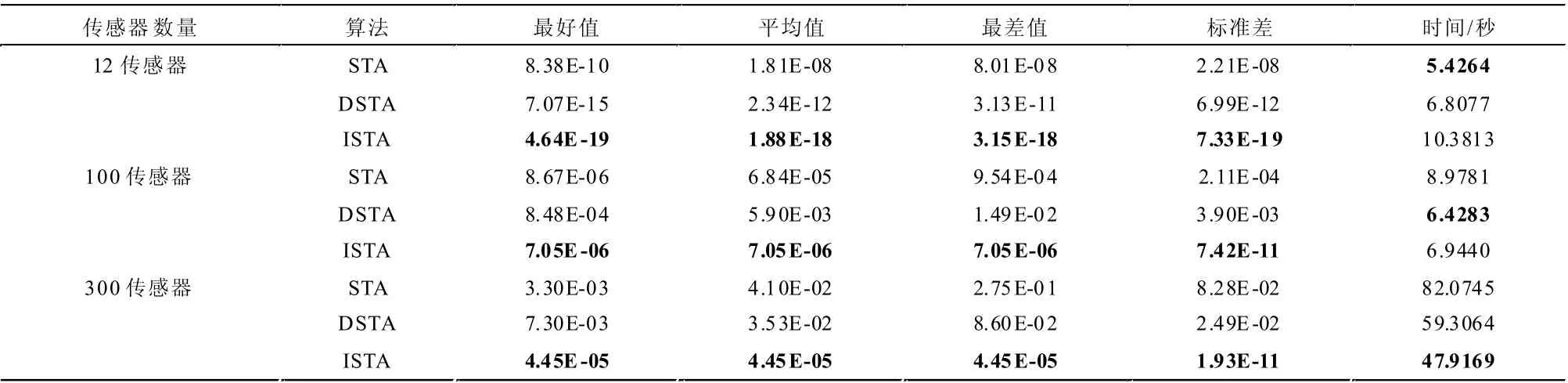
表2 几种算法在SNL 实例上的求解结果
5 结论
本文提出了一种改进的状态转移算法来求解全局数值优化和传感器网络定位问题。该算法采用二次插值技术代替平移算子进行局部搜索,提高了STA 的局部搜索能力。另外,采用随机新变异策略,减小算法陷入局部最优解的可能性。数值实验表明,与其他5 种随机优化算法相比,ISTA 具有更强的局部和全局搜索能力和较快的收敛速度。采用梯度技术增强的ISTA 在求解大规模SNL 问题的结果表明,与基本STA 和DSTA 相比,所提算法的性能也有显著提高。在未来的工作中,该算法可以扩展到多目标优化、约束优化、组合优化和更复杂的现实问题。
