孤岛运行下垂逆变器二次调频方法

董家伟，王志新，朱国忠，包 俊

（1. 上海交通大学 电气工程系，上海 200240；2. 上海正泰电源系统有限公司，上海 200210；3. 上海禧龙科技股份有限公司，上海 201517）

0 引言

微电网及其应用有利于提高对风电、光伏等分布式可再生能源的消纳能力。分布式可再生能源通过逆变器实现电力变换［1-2］，微电网存在并网和孤岛运行2 种方式，因此，也要求逆变器具有并网和孤岛运行2种工作模式。

在孤岛运行工作模式下，逆变器除了作为可再生能源发电设备提供电能，还要为微电网提供电压与频率支撑［3］。下垂控制作为一种分布式的控制方案，可以自动实现微电网内多逆变器的功率平衡分配，其实质是通过控制方法模拟同步发电机的下垂特性，使得逆变器获得类似于同步发电机的一次调频功能，而代价是在功率不匹配情况下带来稳态频率和电压静差［4-5］。对于由同步发电机构成的电网系统，稳态频率静差是通过二次调频环节来消除的，即通过提高或降低同步发电机出力消除稳态频率静差。而对于逆变器，其二次调频调压是通过平移下垂曲线的方法来实现的。

现有研究主要采用通信的方法，如一致性算法等实现多并联逆变器微电网的二次调频。文献［6］提出通过平移下垂曲线进行孤岛下垂微电网的二次调频调压控制，其是采用基于通信的一致性算法实现的。文献［7］设计一种基于二次型最优控制和一致性算法的方法用于频率电压的二次调节。文献［8］设计基于线性自抗扰控制方案的微电网时频电压控制策略。由于下垂环路对多并联逆变器系统的稳定性影响很大，将通信环节加入下垂环将对系统稳定性产生较大影响。此外，逆变器下垂系数的取值需满足一定范围要求，否则将造成系统不稳定［9］。

对于孤岛多并联逆变器微电网运行问题，保障功率分配平衡的前提是保障孤岛多并联逆变器的小信号稳定。分析孤岛小信号稳定性的方法主要有阻抗法［10-13］和状态空间法［14-15］2 种。状态空间法由于可以直观显示各类参数对系统稳定性的影响，如下垂系数等对稳定性的影响［16-17］，因此常用于控制方案的稳定性分析。文献［18］分析并网电感对下垂逆变器稳定性的影响。文献［19］设计一种并网逆变器模型降阶的方法。组件连接法［20-21］是从状态空间法发展出的用于研究系统整体稳定性的方法。本文将基于状态空间法和组件连接法进行分析。

本文提出一种不含通信的孤岛下垂逆变器二次调频方法。该方法在消除孤岛下垂逆变器稳态频率静差的同时，可以提高逆变器的下垂系数稳定范围，从而提高下垂控制逆变器的稳定性。

1 含有二次调频调压项的下垂控制

下垂控制是一种自动均衡多并联逆变器之间有功和无功分配的控制方案。对于由n台逆变器构成的微电网系统，第j台逆变器满足的下垂关系为：

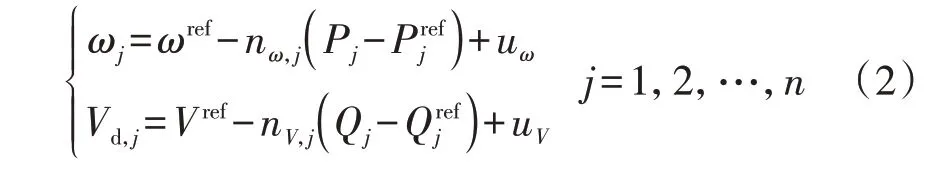
式中：uω和uV分别为二次调频、调压分量，为使得各台逆变器的下垂特性曲线仍交于一点，各台逆变器的二次调频、调压分量需保持一致［22］。根据图1，引入二次调频分量本质上相当于将下垂特性曲线上下平移。当孤岛运行的多并联逆变器系统负荷不变时，各台逆变器的有功分配不变，因此通过二次调频分量uω平移下垂曲线将使得多并联逆变器的静态频率工作点同方向同数值移动，即：

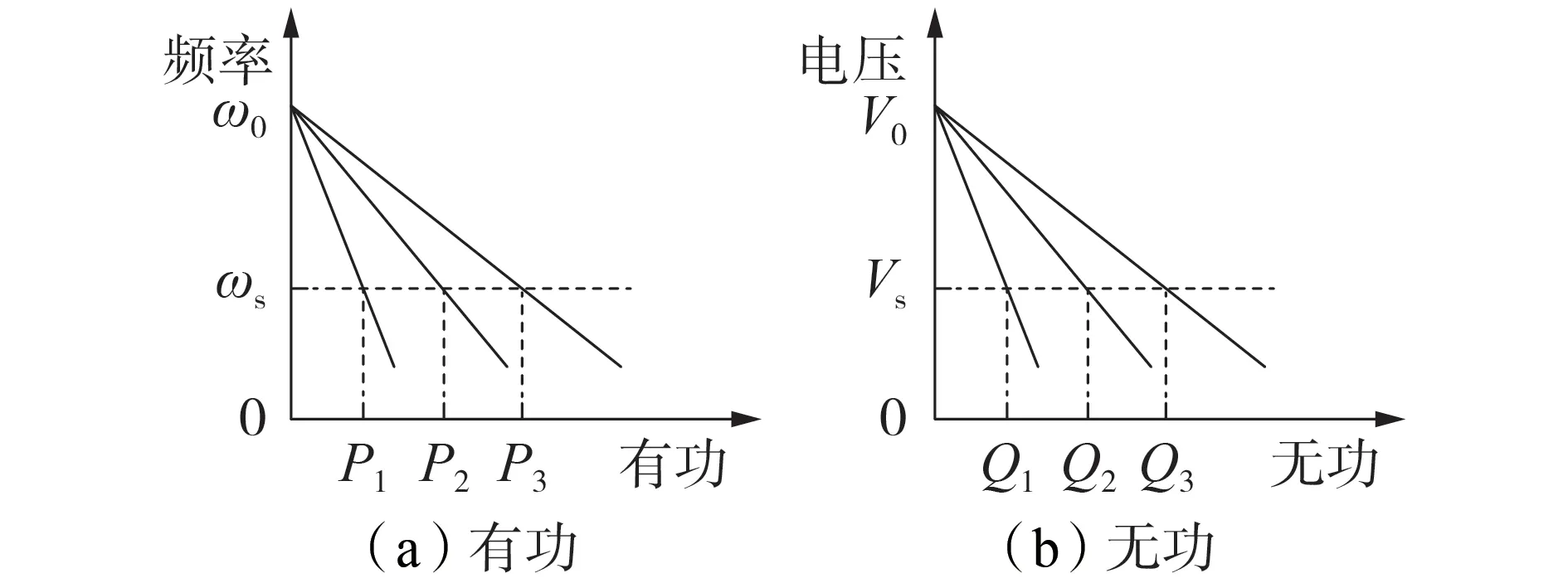
图1 下垂曲线示意图Fig.1 Schematic diagram of droop curves

式中：Δωs为静态频率的补偿量。据此，本文设计一种无需通信的孤岛多并联下垂控制逆变器二次调频方案，从而实现孤岛运行的多并联逆变器系统的频率无静差控制。需要注意的是，理想情况下相同的方案可以应用于系统的电压无静差控制，但由于实际系统中存在线路压降，且线路压降与逆变器出口电压相关，因此线性的平移无法同时实现电压调整与无功分配平衡［23-24］。因此，本文所提方法仅针对孤岛多并联逆变器的二次频率调节。

2 基于积分超前矫正器的二次调频稳定器方法

为实现孤岛运行的多并联下垂逆变器系统的无静差二次调频，同时加强孤岛多并联下垂逆变器系统的小信号稳定性，本文提出采用基于积分超前矫正器的二次调频稳定器对静态频率差进行补偿，表达式为：

式中：uω，j为第j台逆变器的调频分量；T1、T2为超前校正器的2个时间常数，且有T1＞T2。所提控制方法框图如图2 所示，图中Uc，abc，j、I2，abc，j分别为第j台逆变器的输出电压与输出电流。

图2 基于积分超前矫正器二次调频模块的有功频率下垂方法框图Fig.2 Block diagram of active power droop method based on secondary frequency regulation module of integral lead corrector

根据内模原理［25］，矫正器中零极点的作用在于消除频率静差。超前校正环节能提高频率静差补偿的响应速度以及下垂系统的小信号稳定性。类比同步发电机系统中的调频装置［26］，本文提出的积分超前矫正环节功能对应于同步发电机的二次调频装置以及电力系统稳定器PSS（Power System Stabilizer）。超前校正环节的波特图如图3所示。

图3 超前矫正环节的波特图Fig.3 Bode diagram of lead correction part

最大校正相位φmax及其对应频率ωmax分别为：

由图3 可知，超前矫正环节将在矫正频率附近为系统提供一个较大的相位补偿。当矫正频率接近系统剪切频率时，该相位补偿将有效提高系统的相位裕度，从而实现系统稳定性的提升。基于该原理，本文采用超前矫正器对调频环节进行稳定性矫正和增强，确保二次调频过程中多逆变器并联系统的稳定性不受下垂曲线动态调节的影响。

下面本文将基于小信号状态空间分析法和组件连接法，对基于积分超前校正的二次调频模块参数进行设计，并对稳定性进行分析［15-16］。

3 参数设计与稳定性分析

考虑3 台逆变器并联运行的情况，附录A 图A1为所研究的多并联逆变器系统的模型图，图A2为下垂控制器的控制系统框图。本文控制系统采用经典的P-ω、Q-V下垂控制，并考虑虚拟阻抗环路增强系统稳定性。控制内环采用同步dq坐标系下的电流、电压双闭环结构，电流内环采用P 控制，电压外环采用PI控制。按照图A2可以建立详细的系统小信号模型。

3.1 包含二次调频环节的多并联微电网系统小信号模型

式中：Δxfilt为滤波器小信号状态空间变量；Δi1，dq为逆变器侧电感电流d、q轴分量的小信号；Δuc，dq为电容电压d、q轴分量的小信号；Δi2，dq为网侧电感电流d、q轴分量的小信号；Δus，dq为逆变器端口输出电压d、q轴分量的小信号；ΔuPCC，dq为公共耦合点（PCC）处电压d、q轴分量的小信号；Δω为逆变器对应频率的小信号；Af、Bf1、Bf2、Bf3为参数矩阵，表达式见附录B 式（B1）。需要注意的是，尽管逆变器采用LCL 滤波器，但对于下垂控制而言，终端控制目标为电容电压而非网侧电感电流。内环控制器小信号模型如式（7）所示。

对于下垂环，由于功率为电流变量与电压变量的乘积，且坐标变换使用的相位变量与频率变量相关，因此下垂环是非线性控制环路。为建立小信号状态空间模型，需要对下垂环进行线性化。基本的下垂环方程为：

式中：Ainv，j、Binv，j、Cinv，j为参数矩阵，表达式见附录B式（B5）；Δxinv，j、Δxσ，j、Δxv，j、Δxdroop，j为第j台逆变器的状态变量；Δyinv，j为第j台逆变器的输出；Δi2j，dq为第j台逆变器的输出电流。

根据组件连接法，对单台逆变器模型进行组合即可得到仅包含逆变器的系统模型，即：

式中：Δxg为电网模型对应的状态变量；Ag、Bg、Cg、Dg为电网状态空间模型对应的参数矩阵；Rload为阻性负荷电阻；J2为2阶单位矩阵。实际中，阻性或电阻、电容、电感相互并联的阻抗形式均为最小相位环节，因此均可写成式（15）的形式，而电阻、电感串联的比例微分阻抗形式可近似看作额外并联了一个很大阻值的电阻，从而简化为最小相位环节并整理为式（15）的形式。由于本文采用纯阻性负荷，因此，式（15）中Δxg的维度为0，Ag、Bg、Cg均为空矩阵，即电网络方程仅由代数方程构成，不包含微分方程。结合式（13）和式（15）可得到：

式（18）即为本文讨论的多并联逆变器系统的小信号模型。

3.2 基于特征值分析的方案参数设计与稳定性分析

系统参数在附录A表A1、表A2和表1中列出，下文若无特别说明，则参数值均与这些表中相同［6］。

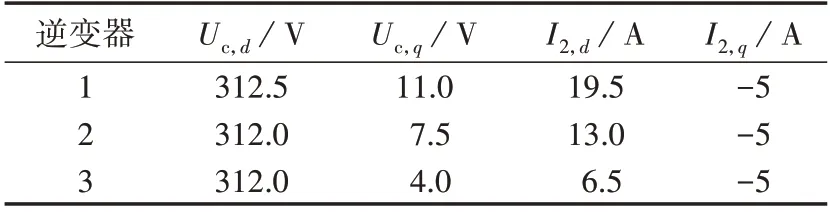
表1 逆变器稳态运行点Table 1 Stable operation point of inverters

根据以上模型绘制参数Tα与α变动时系统的特征值轨迹图，绘图时忽略左半平面远离虚轴的特征值，结果如附录A 图A3 所示。由图可以看出，随着Tα增大，多并联下垂逆变器系统的特征值会向右半平面移动，但始终不会穿过右半平面。对于参数α，由于超前校正环节的限制，α＜1。当α从接近1的数值减小时，特征值会明显向左半平面移动。

在图A3特征值模拟计算的参数设置条件下，即使不使用该超前校正环节，多并联逆变器系统也是稳定的。此时本文设计的环节仅作为二次调频模块使用，不体现其稳定性增强的功能。下面测试当下垂参数设置得过大导致系统原本就处于小信号不稳定状态时所设计环节对稳定性的校正作用。将逆变器1—3 的有功下垂系数均扩大10 倍，分别变为1.20×10-4、6.00×10-5、4.00×10-5Hz／W 时，系统特征值轨迹图如附录A 图A4所示。由图可见，超前校正模块对原本不稳定的多逆变器系统有很好的稳定性校正能力，该校正能力主要取决于分母时间常数与分子时间常数的比值α。随着Tα增大，系统特征值向右半平面移动，但移动范围很小。而随着α减小，系统特征值快速向左半平面移动。从物理意义上而言，较小的α值对应的超前校正环节更近似于一个微分环节，能够给予系统更大的相位补偿。

尽管理想情况下多逆变器并联运行时的有功功率分配与各下垂系数成反比，而与下垂系数的具体值无关，但较小的下垂系数会导致功率分配受其他因素（如线路呈现阻性）干扰，因此较大的下垂系数更有利于稳态功率的精确分配。综上，为保障系统有较好的动态性能，同时使逆变器下垂系数可在较大的范围内进行调整，本文选取参数Tα与α的值分别为1.5 s和0.0165，即式（4）中，T1=1.5 s，T2=0.02475 s。

4 仿真验证

下面将通过MATLAB／Simulink 仿真验证本文所提方法的可行性。基于附录A 图A1 建立仿真系统，采用8 Ω 纯阻性负荷。此外采用自适应虚拟电阻技术对逆变器控制模式的切换过程进行阻尼，使虚拟电阻Rv从300 mΩ变化至3 mΩ。

4.1 控制模式切换性能分析

首先分析本文所提方法在控制模式从并网运行切换至孤岛运行时的切换性能。初始时刻，逆变器1—3 均运行于并网PQ 运行模式，其有功输出分别设定为5、12、13 kW，无功输出均设定为0。1 s 时系统内逆变器运行模式切换为孤岛下垂运行模式，下垂参数如附录A表A2所示。

仿真结果如附录A图A5所示。由图A5（a）可以看出，本文所提方法不会影响逆变器的功率分配，3台逆变器的有功依然满足P1∶P2∶P3=1∶2∶3 的关系。由图A5（b）可以看出，采用本文所提方法可以有效地将下垂控制带来的稳态频率偏差减小至0。同时由图A5（c）、（d）可以看出，在控制模式切换时，采用本文所提方法对输出电压、电流的冲击较小，且动态响应时间在1 s内，响应速度较快。

4.2 与传统下垂控制性能对比

当各台逆变器下垂系数满足小信号稳定性要求时，仿真结果如附录A 图A6 所示。5 s 前系统运行于传统下垂控制模式，5 s 时将本文所提方法应用于控制系统中。由图A6（a）可以看出，采用本文所提方法不会改变多并联逆变器系统输出有功功率的分配比例，这是本文所提方法可行的重要前提条件。由图A6（b）可以看出，在应用本文所提方法前，逆变器系统存在明显的频率静差，这是由下垂控制的特性造成的，而在应用本文所提方法后，并联逆变器系统的频率静差得到快速补偿，并最终达到稳态无静差的效果。因此本文所提方法是有效的。

图4 为在逆变器下垂系数不满足小信号稳定条件下的仿真结果。在图4（a）中，1 s 前3 台逆变器运行于并网运行模式，1 s 时系统切换至传统下垂控制模式，由图可以看出，此时逆变器功率输出以及频率快速发散，呈现出不稳定性质。当采用本文的调频校正模块后，仿真结果如图4（b）所示，模块参数T1=1.5 s、T2=0.024 75 s，由图可以看出，此时不仅系统可以稳定，而且逆变器输出功率仍满足下垂系数之比要求，稳态频率静差也被消除。因此本文所提方法可以在消除稳态频率静差的同时有效提升下垂控制系统的稳定性。

图4 下垂系数初始不稳定条件下本文所提方法与传统下垂控制效果对比Fig.4 Effect comparison between proposed method and conventional droop control under initial unstable condition of droop coefficient

4.3 参数变化影响与小信号模型验证仿真

下面对小信号分析得出的结论进行仿真验证。逆变器1—3 的下垂系数分别设定为1.20×10-4、6.00×10-5、4.00×10-5Hz／W。这些下垂系数对于不采用本文所提方法的传统下垂逆变器是不稳定的，这从图4与附录A图A3的结果均可以得到验证。

仿真结果如图5 所示。由图5（a）—（c）可以看出：参数Tα的值对系统稳定性影响不大，这与小信号分析得到的结论类似，Tα值主要影响系统动态响应的时间；采用超前校正环节后频率的响应可以明显分成快速响应和低速调节2 个过程，在控制模式切换后很短的时间内就可以使得频率回调至接近参考值，该回调过程是一个低速的调节过程，Tα值越大，这2 个过程的区分越明显。由图5（d）—（f）可以看出，参数α的值显著影响含有调频校正环节的下垂控制逆变器系统的稳定性。根据小信号分析可以得出各参数设置下主系统主特征值（即实部最大的特征值）实部：Tα=1 s、α=0.01时，系统主特征值实部为-0.500 3；Tα=1 s、α=0.062 8 时，系统主特征值实部为0.1035；Tα=1 s、α=0.1时，系统主特征值实部为2.69。由仿真结果也可看出，后2种情况出现了小信号不稳定的现象。因此，前文小信号分析得出的结论与仿真结果是吻合的。

图5 不同参数设置下系统仿真结果Fig.5 System simulative results under different parameter settings

4.4 与含通信的二次调频方法对比

文献［6］提出基于一致性算法的二次调频方法，本节将对比本文所提方法与该方法的性能差异。将逆变器1—3 的下垂系数分别设定为1.2×10-5、6.0×10-6、4.0×10-6Hz／W（该参数下系统小信号稳定）。仿真结果如附录A 图A7所示。由图可见，在本文参数设定条件下，本文所提方法的响应速度慢于文献［6］中的方法，采用文献［6］中方法的调节时间约为1 s，采用本文所提方法的调节时间约为5 s。然而由于本文所提方法不采用通信实现，因此实际应用中将比文献［6］中的方法更易实现，且本文所提方法还可提升下垂系数的稳定范围。由图A7（b）、（d）可见，采用本文所提方法不会影响逆变器之间的功率分配。因此，本文所提方法是有效的。

5 结论

本文提出一种无需通信的孤岛运行多并联逆变器下垂二次调频方法，通过基于积分超前校正环节的二次调频稳定器，消除了孤岛多并联下垂逆变器系统频率静差，提高了多并联下垂逆变器系统的稳定性，扩大了下垂系数的稳定域范围。同时，采用组件连接法建立多逆变器并联运行系统的详细小信号状态空间模型，设计了积分超前环节参数，并分析了相关参数对多逆变器并联运行系统稳定性的影响。分子时间常数T1增大使得特征值绝对值减小，分子时间常数与分母时间常数之比T1/T2对稳定性的影响较为显著。通过与采用通信方案的二次调频方法进行比较发现，本文所提方法在响应速度上稍慢于采用通信方案的二次调频方法，但在具体实现上由于无需在逆变器之间进行实时通信，因此，显著降低了多并联逆变器系统的通信压力。

附录见本刊网络版（http：//www.epae.cn）。