基于矩阵的迹的弱电网下永磁直驱风电场直流电压时间尺度小扰动振荡稳定性分析

2022-05-11刘克权刘文飞郝如海陈仕彬

电力自动化设备 2022年5期

刘克权，刘文飞，刘春，郝如海，陈仕彬，高振，王洋

（1. 国网甘肃省电力公司，甘肃兰州 730070；2. 国网甘肃省电力公司电力科学研究院，甘肃兰州 730070；3. 四川大学电气工程学院，四川成都 610065）

0 引言

大规模风力发电并网的安全与稳定运行对加快推动实现“双碳”目标起到关键作用。风力发电系统的电气部分主要基于电力电子变流器的矢量控制实现功率和电压的解耦［1］。随着风电并网容量占比的升高，电力系统的电力电子化程度愈发明显，由风机换流器控制环节引发的系统振荡失稳问题给电网安全稳定运行带来了极大的隐患［2-5］。弱电网下永磁直驱风电场的并网稳定性问题主要受网侧换流器（GSC）动态的影响［6-7］，永磁直驱风机（PMSG）换流器控制系统主要采用基于dq坐标系的电流矢量控制策略，通过三相同步锁相环（PLL）定位dq坐标系与电网xy公共坐标系下的相角，从而保证风机系统与外部电网同步运行［8-10］。

文献［11］研究了电流时间尺度下由PLL 与网侧换流器电流环的交互作用所引发的弱电网下PMSG系统小扰动稳定性问题。文献［12-13］研究结果表明，在直流电压时间尺度下PMSG 小扰动稳定性主要由直流电压动态所对应的二阶线性系统主导。然而，以往研究表明PLL 的带宽可以在较宽的频带范围内变化。弱电网下，当PLL 带宽与PMSG 网侧换流器的直流电压环带宽相接近时，二者强交互作用将引发直流电压环对应模式的阻尼进一步恶化甚至引发小扰动失稳［14-16］。文献［14］通过建立PMSG 的状态空间模型，利用特征值法研究线路电抗和有功功率变化对直流电压动态主导的PMSG 次同步振荡的影响，算例结果显示当线路电抗或风机有功出力增大时，系统参数安全域面积越窄，系统阻尼越差。文献［15］通过建立考虑网侧换流器直流电压、无功控制外环和PLL 动态的降阶模型，研究了弱电网下各控制环的交互作用，研究结果表明在直流电压时间尺度下，PLL 与直流电压环的动态交互作用是导致PMSG 系统小扰动稳定性进一步恶化的主要原因。然而以上文献主要通过模式分析法分析PMSG系统小扰动稳定规律，所得结论缺少理论依据。文献［16］通过建立直流电压时间尺度下永磁直驱风电场降阶模型，结合Routh-Hurwitz 稳定判据定量研究了弱电网下永磁直驱风电场在直流电压时间尺度下的小扰动稳定极限问题，其研究的局限性在于所得稳定极限解析式过于复杂，仍需借助计算机进行辅助分析。文献［17］分析了可对风电场进行单机等值的理论依据和成立条件，并提出了可用于振荡分析的风电场动态等效模型。文献［18］利用风电场单机等效模型，建立保留PLL 和线路动态的二阶PMSG模型，推导得到永磁直驱风电场小扰动稳定极限的解析式，利用解析结果解释了弱电网下永磁直驱风电场由PLL动态主导的小扰动稳定性受风机有功出力和风机数量等因素影响的规律。

本文尝试从理论角度揭示弱电网下永磁直驱风电场直流电压时间尺度小扰动稳定性规律。首先建立考虑PLL和直流电压环动态的永磁直驱风电场等效降阶模型；然后基于降阶模型状态矩阵的迹的解析式，分析得到弱电网下永磁直驱风电场等效降阶系统全部模式总阻尼受线路电抗、风机数量和风机无功出力等运行参数的影响规律；最后通过非线性时域仿真算例验证本文所得结论的正确性。

1 并网永磁直驱风电场的闭环模型

1.1 并网永磁直驱风电场模型

图1 为含N台PMSG 的永磁直驱风电场拓扑结构图，风电场整体呈现放射状拓扑结构，共含有M条汇流支路，各汇流支路将风机发电功率经母线汇集后通过远距离交流输电线路馈送至受端交流电网。图中，xL为交流线路电抗。

图1 含N台PMSG的并网永磁直驱风电场结构图Fig.1 Structure diagram of grid-connected PMSG wind farm with N PMSGs

风电场中第k台（k=1，2，…，N）PMSG 的n阶线性化状态空间模型可表示为：

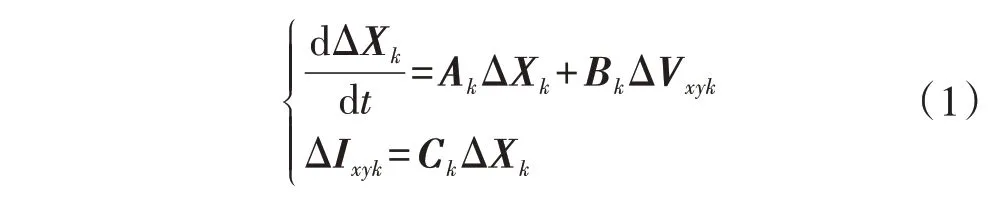
式中：ΔXk为第k台PMSG 的状态向量小扰动分量；ΔVxyk和ΔIxyk分别为xy公共坐标系下第k台PMSG 的端口电压和输出电流向量的小扰动分量；Ak、Bk和Ck分别为第k台PMSG 的系统状态矩阵、输入矩阵和输出矩阵。

若将受端交流电网视为理想电网，则各风机的端口电压与输出电流之间的网络关系可表示为［16］：

式中：xij（i，j=1，2，…，N）为风电场网络矩阵Xnet中的元素，Xnet如式（4）所示。

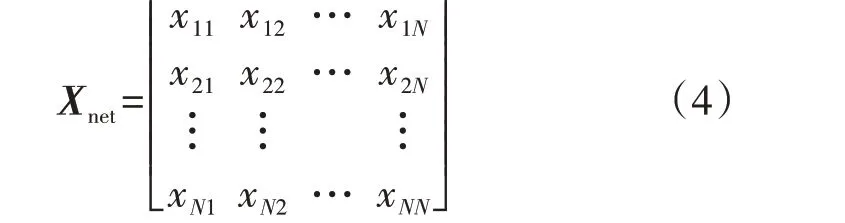
风电场网络矩阵形成原则［18］简述如下：自阻抗xii为第i台风机所发电流从PMSG 的端口到受端理想电网所流经线路的阻抗之和；互阻抗xij为第i台风机和第j台风机所发电流公共流经线路的阻抗之和。

将各风机状态空间模型（式（1））与风电场网络矩阵模型（式（2））联立可得并网永磁直驱风电场的闭环模型为：

式中：k=1，2，…，N；di[Ak]、di[Bk]和di[Ck]分别为Ak、Bk和Ck的分块对角阵。

1.2 并网永磁直驱风电场等效子系统模型

当风电场规模不大，各风机由同一厂家生产时，风机参数和输出功率等基本相同。由于本文主要研究风机数量和交流输电线路电抗对系统稳定性的影响，不研究风电场汇集系统拓扑结构和汇集线路参数的影响，故有如下合理假设条件：

1）风电场内所有风机的线性动态方程相同；

2）忽略风电场汇集系统拓扑结构和汇集线路参数的影响。

关于上述2 条假设对并网风电场系统小扰动稳定影响规律，文献［17］已进行了详细的研究，本文不再赘述。

根据以上2 条假设，可将原阶数为N×n的高阶风电场模型通过等效变换解耦为阶数等于单台并网风机的动态等效子系统模型（阶数为n），并用其来研究原并网风电场的小干扰稳定性问题［18］。由假设1）可知风机具有完全相同的线性化方程，此时有Ak=Ap，Bk=Bp，Ck=Cp（k=1，2，…，N）。因此，可将式（5）所示的N×n阶并网风电场模型变换为如下N个独立的n阶等效子系统：

根据式（10）可知等效子系统模型可表示为单台PMSG经线路电抗NxL接入理想交流电网。

1.3 考虑PLL 和直流电压动态的永磁直驱风电场等效子系统模型

由文献［15］可知，研究弱电网下永磁直驱风电场直流电压时间尺度的小扰动稳定性时，PLL 与直流电压模式强交互作用对由直流电压动态主导的PMSG 小扰动稳定性具有明显影响。故为降低模型阶数，简化推导过程的同时考虑PLL 对直流电压环的交互作用，将阶数为n的全阶模型（式（10））降阶为考虑PLL 动态和直流电压环动态的四阶模型。图2 为dq坐标系下风电场中第k台PMSG 的结构示意图。图中：Vk、θk分别为第k台PMSG的机端电压幅值、相角；Idk、Iqk分别为第k台PMSG 输出电流的d、q轴分量；Pmk、Pk分别为第k台PMSG 的直流电容输入侧、输出侧的有功功率；Vdck为第k台PMSG 直流电容电压；Cdck、Xfk分别为第k台PMSG 的直流电容、滤波电抗；θpllk为第k台PMSG的PLL输出相角。

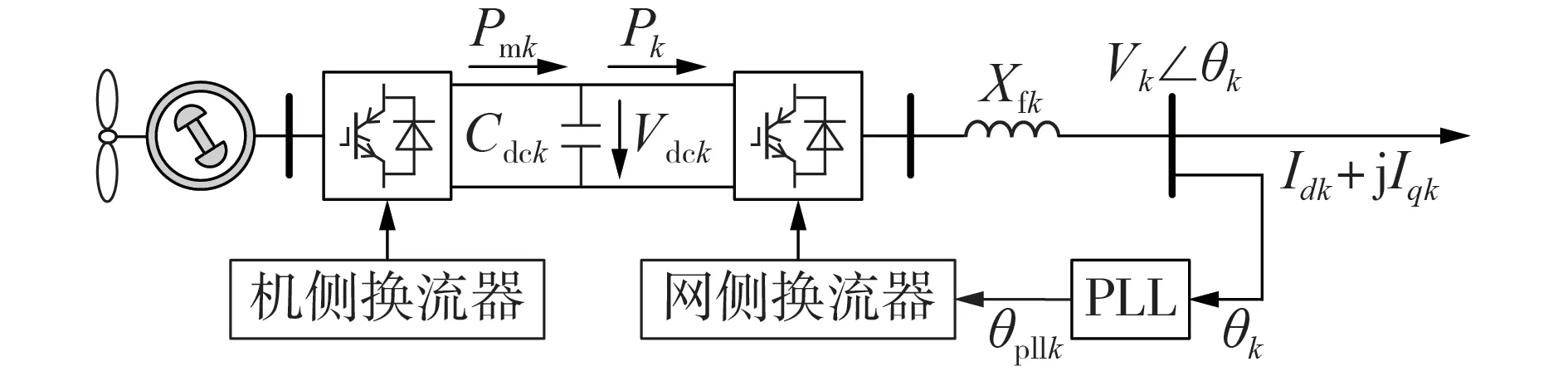
图2 第k台PMSG的结构示意图Fig.2 Structure schematic diagram of PMSGk

建立保留PLL 和直流电压动态的PMSG 降阶模型时，有如下合理假设条件［16，18］：

1）忽略脉宽调制（PWM）动态的影响；

2）由于网侧换流器内环电流动态比外环电压的动态至少快10 倍，故可以忽略内环电流动态的影响；

3）忽略PMSG永磁机和机侧换流器的影响；

4）忽略网侧换流器无功外环的动态过程；

5）忽略不计换流器的内部功率损耗。

PLL 采用目前广泛应用的三相同步PLL 控制策略，其工作原理和小信号控制框图分别如图3（a）、（b）所示。图中：Kp_pllk和Ki_pllk分别为第k台PMSG 锁相环PI 控制器的比例系数和积分系数；Δθk和Δθpllk分别为第k台PMSG 机端电压相角小扰动分量和PLL 输出相角小扰动分量；Δxpllk为第k台PMSG PLL积分状态变量小扰动分量；F（s）为低通滤波器传递函数；Vk0为第k台PMSG机端电压幅值的稳态值。

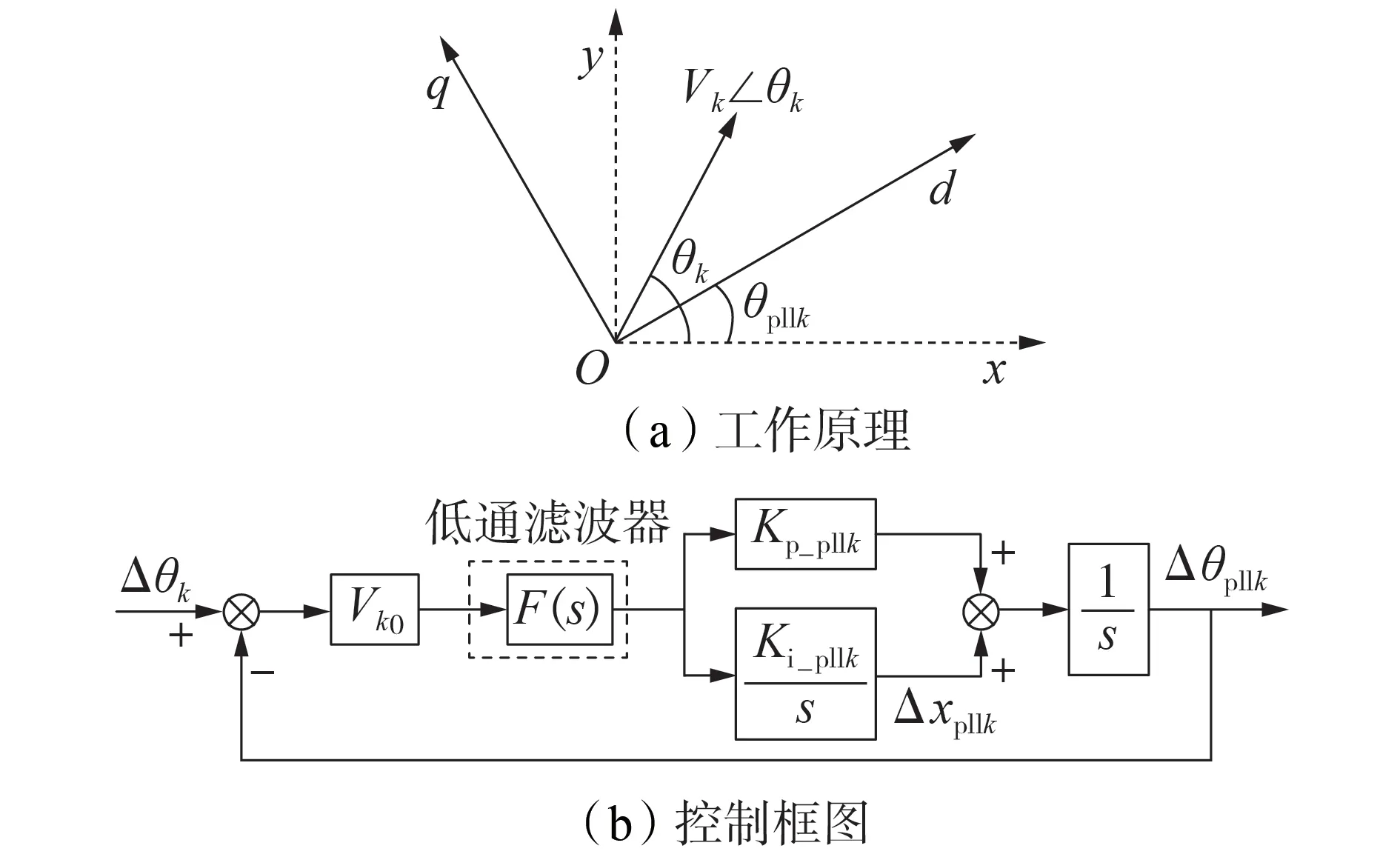
图3 PLL工作原理和小信号控制框图Fig.3 Operating principle and small signal control block diagram of PLL

由图3（a）可得机端电压相角与xy公共坐标系下电压分量的关系为：

图4 PMSG网侧换流器矢量控制模型Fig.4 Vector control model of GSC for PMSG

式中：Q0为风机输出的无功功率稳态值。

将式（16）代入式（10），可得考虑PLL 和直流电压动态的永磁直驱风电场等效子系统的四阶状态矩阵的详细表达式如式（17）所示。

式中：I0为风机输出电流幅值的稳态值。

2 保留PLL 和直流电压环动态的永磁直驱风电场小扰动稳定性规律

根据矩阵论中相关理论可知，m×m阶矩阵的迹定义为矩阵主对角元素之和，其值等于矩阵全部特征值之和。设PLL 和直流电压环模式分别为λPLL=ξPLL±jωPLL和λdc=ξdc±jωdc。则四阶状态空间矩阵AzN的迹为：

由式（22）可知，当风机控制参数、直流电容和直流电压参考值固定不变时，风机数量N、线路电抗xL、风机无功出力Q0对并网永磁直驱风电场等效子系统状态空间矩阵的迹的影响规律为：

1）当其他参数不变，线路电抗xL增大时，Tr(AzN)向正方向移动，说明PLL 和直流电压环二者至少有1 个模式的阻尼降低；

2）当其他参数不变，风机无功出力Q0增大时，Tr(AzN)向正方向移动，说明PLL 和直流电压环二者至少有1个模式的阻尼降低；

3）当其他参数不变，风机数量N增大时，Tr(AzN)向正方向移动，说明PLL 和直流电压环二者至少有1 个模式的阻尼降低。

实际上根据以往研究成果可知，弱电网下永磁直驱风场直流电压时间尺度小扰动稳定性主要由直流电压动态主导［12-13］。故由以上3 条规律并结合以往研究成果可进一步推理出如下结论：考虑PLL 和直流电压动态交互作用时，系统运行参数（xL、Q0或N）增大，弱电网下永磁直驱风电场的直流电压环这一主导模式阻尼减弱。关于该结论的正确性可进一步通过阻尼转矩分析法进行论证，详见附录A。

3 算例分析

本文算例系统用10台PMSG并联结构的并网永磁直驱风电场，其中PMSG 用文献［16］给出的十五阶模型和参数，单台风机默认有功出力P0=0.25 p.u.，无功出力Q0=0.05 p.u.，线路电抗xL=0.07 p.u.。在此基础上研究风机无功出力Q0、线路电抗xL和风机数量N的变化对并网风电场稳定性的影响规律。仿真平台采用的是MATLAB 2014a。

3.1 降阶模型的仿真验证

以风机无功出力Q0变化为例，对比用全阶模型与降阶模型时PLL 和直流电压环模式的差异，以验证本文所推导的降阶模型（即式（17））的合理性。当单台风机有功出力P0=0.25 p.u.，线路电抗xL=0.05 p.u.，风机数量N=10，无功出力Q0从0.04 p.u.增大到0.12 p.u.时，全阶模型和降阶模型下2种模式的计算结果如图5所示。

图5 2种模式的计算结果Fig.5 Calculative results of two modals

由图5 所示的模式对比结果可知，当直流电压环与PLL 带宽接近时，在弱电网下随着无功出力的增大二者发生近似强模式谐振，导致直流电压环模式下的阻尼减弱甚至发生失稳现象。由图5 可知，本文所推导的降阶模型与全阶模型的模式轨迹变化趋势基本一致，可以用来研究弱电网下永磁直驱风电场的小干扰稳定性问题。

3.2 输电线路电抗xL对风电场小干扰稳定性的影响

根据第2 节所得影响规律1），输电线路电抗xL增大会导致并网永磁直驱风电场PLL或直流电压环模式下的阻尼降低。在xL从0.05 p.u.增大到0.11 p.u.的过程中，计算并网永磁直驱风电场矩阵AzN的特征值，根据参与因子得到PLL 和直流电压环模式变化规律，如表1所示，表中xL为标幺值。根据表1可知，随着xL增大，直流电压环模式下的阻尼逐渐变弱直到失稳，矩阵的迹随着xL的增大不断向正方向移动，这与第2节所描述的规律是一致的。

表1 xL变化时2种模式的计算结果Table 1 Calculative results of two modals with variation of xL

0.5 s 时，风机有功出力发生小扰动，并在0.55 s时切除扰动，得到非线性仿真结果如图6 所示，图中永磁直驱风电场输出有功功率为标幺值。由图6 可知，当xL=0.09 p.u.时，永磁直驱风电场有功出力发散失稳，这与表1所示的结果一致。

图6 非线性仿真结果Fig.6 Nonlinear simulative results

3.3 PMSG 无功出力Q0对风电场小干扰稳定性的影响

根据第2 节所得影响规律2），风机无功出力Q0增大会导致并网永磁直驱风电场PLL 或直流电压环模式下的阻尼降低。在Q0从0.03 p.u.增大到0.09 p.u.的过程中，计算并网永磁直驱风电场矩阵AzN的特征值，根据参与因子得到PLL 和直流电压环模式下的变化规律见附录B表B1。根据表B1可知，随着Q0增大，直流电压环模式下的阻尼逐渐变弱直到失稳，矩阵的迹随着Q0的增大不断向正方向移动，这与第2节所描述的规律是一致的。

扰动设置与3.3节一致，得到非线性仿真结果见附录B 图B1。由图可知，当Q0=0.07 p.u.时，永磁直驱风电场有功出力波形发散失稳，并网永磁直驱风电场小扰动失稳，这与附录B 表B1 所示的结果相吻合。

3.4 风机数量N对风电场小干扰稳定性的影响

根据第2 节所得影响规律3），风机数量N增大会导致并网永磁直驱风电场PLL或直流电压环模式下的阻尼降低。在N从7 增大到16 的过程中，计算并网永磁直驱风电场矩阵AzN的特征值，根据参与因子得到PLL 和直流电压环模式下的变化规律，见附录B 表B2。根据表B2 可知，随着N增大，直流电压环模式下的阻尼逐渐变弱直到失稳，矩阵的迹随着N的增大不断向正方向移动，这与第2节所描述的规律是一致的。

扰动设置与3.3节一致，得到非线性仿真结果见附录B 图B2。由图可知，当N=13 时，永磁直驱风电场有功出力波形发散失稳，并网永磁直驱风电场小扰动失稳，这与附录B表B2所示的结果相吻合。