基于时间序列与混合核函数SA-SVR的滑坡位移预测模型研究*

尚 敏 熊德兵 张惠强 赵国飞

(①湖北省地质灾害防治工程技术研究中心(三峡大学)，宜昌 443002，中国)(②湖北长江三峡滑坡国家野外科学观测研究站，宜昌 443002，中国)(③三峡库区地质灾害教育部重点实验室(三峡大学)，宜昌 443002，中国)(④三峡大学土木与建筑学院，宜昌 443002，中国)

0 引 言

滑坡地质灾害是当今主要地质灾害之一，对人民生命财产造成严重威胁。构建合理完善的滑坡位移预测模型是实现滑坡地质灾害监测预警的关键技术，能有效减少其给国家和人民造成的重大损失(尚敏等，2019)。因此，科学有效地展开滑坡位移预测模型研究，具有重要的理论意义和现实意义。

根据现有资料，滑坡的预测预报可追溯到20世纪60年代日本学者斋藤(Satio，1969)通过经验公式对滑坡预测的初步探索，其后滑坡预测方法经历了从线性预测到非线性预测的转变(Scheidegger，1973；Murray et al.，1994；韩贺鸣等，2019)。时间序列分解方法以其完善的理论获得广大学者的青睐，根据其分解项的复杂程度不同采用线性或非线性的预测方法，大幅度提高了滑坡灾害预测准确性。该方法主要是基于滑坡位移监测数据、降雨量数据、库水位调度数据等对滑坡位移进行时间序列分解，然后分别对分解的子序列应用模型进行预测。目前提取趋势项的主要方法有：周超等(2015)应用移动平均法，将白水河滑坡累积位移分解为周期项和趋势项，这种方法操作简单，在阶跃幅度基本一致的滑坡上能取得不错的效果；黄海峰等(2014)采用平滑先验法经过简单计算快速分离趋势项和周期项，对白家包滑坡进行了预测，结果表明，在正则化参数取值较小时，其精度高于移动平均法但其正则化参数的取值规律还有待探究；张凯翔等(2017)应用小波变换将滑坡累积位移分解为各个频段，低频分解项即为趋势项位移，小波变换具有不需要先验知识，可以处理具有复杂变化趋势的数据等优点，但其基函数和小波阶次较难确定；邓冬梅等(2017)应用集合经验模态分解白水河滑坡位移，具有不需要事先估计分量的函数类型且适用性高的特点，但该方法需要对累积位移序列、降雨量序列和库水位分别重构，工作量较大，较为复杂。以上方法各有优劣，本文在移动平均法的基础上进行改进，采用指数平滑法对累积位移反复分解，将最后一次分解的结果作为趋势项，克服了移动平均法在累积位移阶跃幅度不一致时分解结果仍保留明显阶跃性的问题。

在周期项的预测上，柳青等(2019)将时间序列和BP神经网络相结合，其预测位移与实际位移曲线较一致；汤罗圣等(2012)采用GM(1，1)预测八字门滑坡位移，杨背背等(2018)采用长短时记忆神经网络(LSTM)对三峡库区白水河滑坡位移进行预测，能更好地反应滑坡演化的动态本质；然而灰色模型缺乏对数据样本的学习过程，神经网络受限于局部最优，收敛速度慢等缺点。支持向量机回归(SVR)具有小样本，多维度，非线性的特点，在滑坡预测预报上获得广泛应用。针对SVR参数寻优困难的问题，学者们采用不同的优化智能算法进行参数寻优，李麟玮等(2018)采用灰狼优化算法(GWO)、杨帆等(2019)采用人工蜂群算法、张俊等(2015)采用粒子群优化算法(PSO)、徐峰等(2018)采用自适应粒子群算法(AMPSO)；在此基础上，本文采用模拟退火算法(SA)进行参数寻优，通过线性核与RBF核构造混合核函数，采用构造后的混合核函数对SA-SVR进行优化，结果表明，混合核函数对SVR预测精度有重要影响。

同时，滑坡影响因子的选取对周期项预测有重要影响。杨背背等(2018)选择当月降雨量、两月降雨量、库水位高程、当月库水位、当月库水位变化、双月库水位变化、当月位移增量、前两月位移增量、前三月位移增量作为周期项预测的影响因子，结合鲁芃等(2017)通过Geo-studio对滑坡渗流场及应力-应变进行数值模拟结果，对比白家包累积位移、降雨和库水位监测曲线，得出白家包滑坡变形对库水位下降更加敏感，变形速率与库水位下降速率正相关的特性。本文在此基础上，对库水位因子进行更加详细的划分，分别为库水位、库水位变化量、两月库水位变化量、库水位下降量、平均库水位、平均库水位变化量、两月平均库水位变化量和平均库水位下降量，经过对比，前4个更能反应周期项的细部变化，后4个更能代表周期项的整体变化趋势。

基于上述研究背景，本文以三峡库区白家包滑坡为例，基于时间序列分解原理，通过指数平滑法反复分解累积位移序列，将最后一次分解所得结果作为趋势项；趋势项采用K-flod交叉验证后的3次多项式拟合；周期项采用混合核函数SA-SVR模型进行预测；最后，将预测的趋势项位移和周期项位移叠加，即为滑坡累积位移预测结果，并通过判定系数和均方根误差对模型进行评价。

1 滑坡位移预测模型

1.1 时间序列分析

滑坡位移的产生是一个复杂的非线性过程，按时间序列分解理论可将滑坡位移分解为3个部分：由滑坡自身地质条件(如岩土体类型及成分、地形地貌、地质构造等)决定的趋势项位移，其表现为随时间的单调递增；由外界诱发因素(如降雨、库水位调度等)引起的周期项位移，表现为随时间呈周期性变化；以及由随机事件引起的波动项位移(黄显峰等，2007)。基于对同类型滑坡的研究，波动项的值普遍较小，故本文不对波动项位移进行探究，因此时间序列分解模型可简化为：

S(t)=ψ(t)+η(t)

(1)

式中：S(t)为时间位移序列；ψ(t)为趋势项位移；η(t)为周期项位移。

由于白家包滑坡不同年份阶跃幅度变化较大，采用移动平均法分解所得的趋势项位移仍保留明显的阶跃性，且得到的周期项较难预测。因此，本文反复使用指数平滑法对累积位移进行分解，将第N次分解的趋势项作为最终的趋势项，来获得可以代表滑坡趋势的位移曲线。

指数平滑法是C.C Holt于1958年提出的，在滑坡预测中广泛应用(尹光志等，2007)。指数平滑法是一种特殊的加权平均法，是一种对本期观测值和上期平滑值赋予不同的权重，求得本期平滑值的方法。指数平滑法基本原理如下：

(2)

式中：St为第t期平滑值，也即第t期的趋势项；yt为第t期观测值；St-1为第t-1期平滑值；a为平滑指数。由式(2)可知，当a越接近1时，第t期平滑值越接近第t期观察值。

只使用一次指数平滑法与移动平均法一样难以较好分离趋势项和周期项，因此需要多次使用指数平滑法，其步骤为：

(1)采用指数平滑法将滑坡累积位移分解，获得趋势项1。

(2)将趋势项1用指数平滑法继续分解，获得趋势项2。

(3)多次重复上述步骤，可获得趋势项N，此时周期项即为累积位移与趋势项N之差，当趋势项较平滑且周期项有较好预测效果时，分解结束。

1.2 混合核函数支持向量机回归

支持向量机回归(Support Vector Regression，SVR)是Vapnik于20世纪90年代提出的一种非线性问题回归预测方法(Cortes，1995)。其主要原理是：将样本数据划分为训练样本和预测样本，通过非线性映射函数φ(x)将训练样本映射到高维空间，使得低维空间的非线性问题转化为高维空间的线性问题，然后在高维空间中利用核函数替换映射函数的点积运算，获得具有最优拟合效果的决策函数模型。该决策函数即为SVR回归预测模型，通过预测样本对决策函数进行验证。SVR回归预测模型原理如下：

针对需要训练的样本数据，假定训练样本集为Ω={(x1，y1)，(x2，y2)，…，(xm，ym)}，其中，xi为输入向量，yi为输出向量，则SVR回归预测模型的决策函数可表示为：

f(x)=ωTφ(x)+b

(3)

式中：ωT为权重系数；φ(t)为非线性映射函数；b为偏置量。

求解决策函数的过程可看作求解最小化问题：

(4)

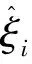
(5)

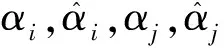
(6)

其中：K(xi，xj)=φ(xi)Tφ(xj)为核函数，通过核函数可以在不确定非线性映射函数φ(x)形式的情况下求得决策函数，极大地提高了SVR模型计算效率，常见的核函数如下：

其中：线性核泛化能力强、学习能力弱，它拥有越是远离测试点对核函数越有影响的特性，是一种全局核，RBF核泛化能力弱、学习能力强，它拥有越是接近测试点对核函数越有影响的特性。此外，核函数还具有以下性质(刘琰，2012)：

(1)若k1为核函数，λ为常数，则λk1也是核函数；

(2)若k1和k2为核函数，则对于任意正数γ1和γ2，其线性组合γ1k1+γ2k2也是核函数；

(3)若k1和k2为核函数，则核函数直积k1k2也是核函数；

本文通过性质(2)构造混合核函数，将泛化能力强、学习能力弱的线性核和泛化能力弱、学习能力强的RBF核函数组合在一起，构造成新的核函数，其形式为：

Kmix=λKploy+(1-λ)Krbf，λ∈[0，1]

(7)

式中：Kmix为混合核函数；Kploy为线性核函数；Krbf为RBF核函数；λ为线性核比例。

1.3 模拟退火算法

模拟退火算法(Simulated Annealing，SA)是美国物理学家S.Kirkpatrick于1983年以Metropolis方法为基础用来解决组合优化问题中最优解问题的一套算法(康立山等，1994)。模拟退火算法模拟了热力学中固体退火过程中，固体在降温后，内能会降到最低，达到一种稳定状态。模拟退火算法是一个“产生新解-判断-接受/舍弃”的过程，其全局寻优能力较强，理论上能以概率1收敛于全局最优解。在寻优初期，能以很大的概率接受一个较差的解从而避免过早寻到局部最优解而结束寻优过程；在寻优后期，这个概率会逐渐减小，从而保证模拟退火算法在后期时的收敛能力(李元香等，2019)。以求解f(x)最小值为例，模拟退火算法详细步骤如下：

(1)初始温度为T0，马尔可夫链长度为L0，在可行解中随机挑选一个初始解x0，此时迭代次数i=0，计算目标函数f(x0)。

(2)用摄动装置产生一次随机扰动，在可行解空间中产生一个新解xi，计算目标函数f(xi)。

(3)用Metropolis准则判断是否接受新解：若f(xi)≤f(x0)时，接受新解xi，此时最优解xp=xi；若f(xi)>f(x0)，则以概率pt接受新解xi，当pt>random(0，1)时，最优解为f(xi)，否则最优解仍为f(x0)。

(4)重复步骤2、3，得到链长为L0过程的最优解。

(5)判断是否满足停止条件，若满足则终止；若不满足则开始下一次迭代，温度为Ti+1=μTi，马尔可夫链长度为Li+1，回到步骤2。

混合核函数SA-SVR预测周期项流程图如图1所示。

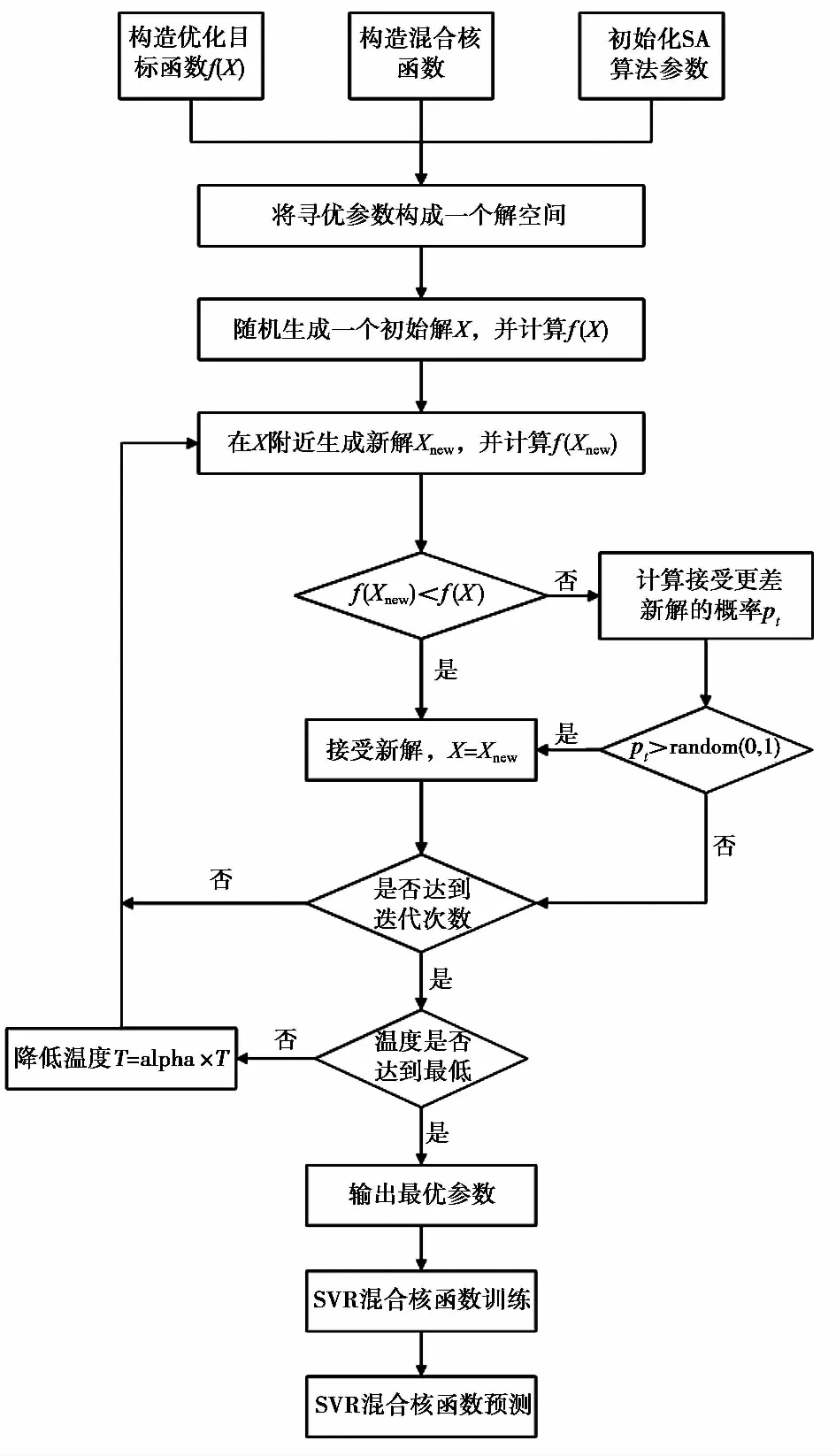
图1 混合核函数SA-SVR位移预测技术路线

1.4 评价指标

判定系数(coefficient of determination，R2)和均方根误差(root mean square，RMSE)在滑坡的位移预测模型中常作为精度评价指标，因此，使用它们来评价预测模型，其定义为：

(8)

(9)

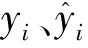
2 白家包滑坡变形特征分析

2.1 白家包滑坡工程地质概况

白家包滑坡位于湖北省秭归县归州镇，位于香溪河右岸，距香溪河入江口2.5 km。白家包滑坡为土质滑坡，坡体为逆向结构，其前缘直抵香溪河，滑坡剪出口位于约高程130 m处，滑坡后缘以基岩为界，高程265 m，滑坡左侧以山脊下部基岩为界，右侧以山梁为界，前缘宽500 m，后缘宽300 m，纵长约550 m，滑坡面积2.2×105m2。

白家包滑坡物质为崩坡积物，坡积物厚度在空间上分布不均，前缘坡积物厚度较厚，滑体物质成分为碎块石土。滑床为基岩，成分为长石石英砂岩、泥岩，产状285°∠30°，滑坡平面形态呈短舌状(尚敏等，2021)。

2.2 白家包滑坡位移分析

白家包滑坡上目前布设ZG323、ZG324、ZG325和ZG326共4个GPS监测点，于2006年9月开始监测，各监测点位置如图2所示，监测位移图像如图3所示。ZG325监测点位于滑坡中上部，ZG324监测点位于滑坡中下部，且位移曲线相较于ZG323和ZG326更具有代表性，能够更好地代表白家包滑坡的整体位移过程，如图2和图3所示。鉴于篇幅有限，因此本文选取ZG325监测点进行详细分析，以ZG324监测点进行对比分析，ZG325监测点累积位移、降雨量和库水位监测曲线如图4所示。显然，白家包滑坡位移随时间呈阶跃式增长，且每间隔几年会有一次较大的阶跃增长。根据库水位的调度情况，白家包滑坡位移可划分为两个阶段：

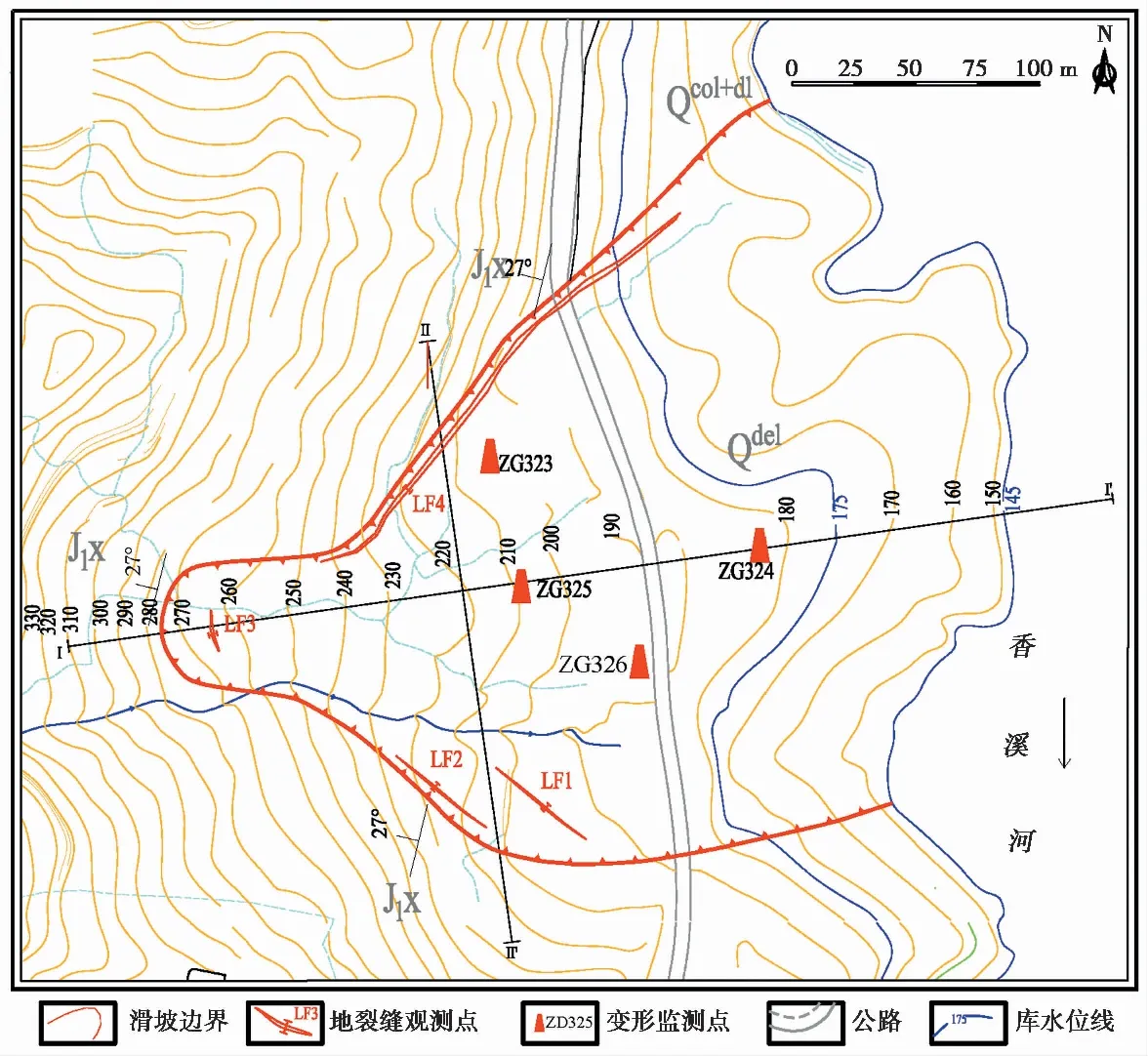
图2 白家包滑坡工程地质平面图

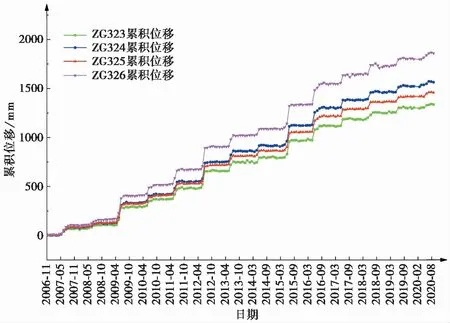
图3 白家包滑坡累积位移曲线图

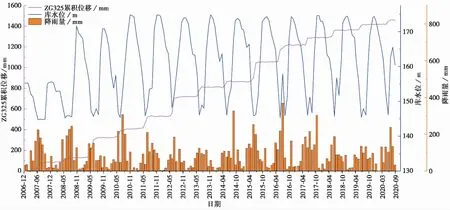
图4 ZG325累积位移-降雨量-库水位监测曲线

(2)2009年4月至2020年9月，库水位峰值由155 m上升到175 m，波动范围为145～175 m，每年8～12月，库水位逐渐从波谷上升到波峰，1～5月，库水位从波峰下降到波谷，6～7月库水位先小幅上升再下降，滑坡在每年5～9月发生阶跃性位移，其中2009年、2011年、2012年、2015年和2016年阶跃较大，分别为178.4 mm、112.1 mm、170.5 mm、182.7 mm、150.4 mm。

综上所述，白家包滑坡为蠕滑-拉裂型滑坡，其变形主要受库水位升降的影响，降雨仅对滑坡变形起推动作用(邓茂林等，2020)，并且库水位和降雨对滑坡的影响是不同步的，具有明显的滞后效应。如图4所示，在8～12月期间，月降雨量逐渐减小，库水位处于上升阶段，又因白家包滑坡坡体黏土渗透性差，坡体受到与坡面正交且指向坡面的渗透水压力，减缓坡体下滑。在1～7月期间，月降雨量逐渐增加，库水位处于下降状态，此时水向坡体外渗透速率远小于库水位下降速率，产生指向坡外的渗透水压力，加剧坡体下滑。值得注意的是，渗透水压力对坡体的响应在时间上存在一定的滞后，8～9月库水位上升时产生的阶跃位移为库水位下降期间的滞后影响造成的。

3 白家包滑坡位移预测

本文取2009年1月～2020年9月的GPS监测数据作为原始数据，但多次使用指数平滑法提取趋势项位移的过程中，会损失一部分数据，因此实际分析时间段为2012年1月～2020年9月。取2012年1月～2019年9月的监测数据作为训练样本集，以2019年10月～2020年9月的监测数据作为预测集。

3.1 趋势项位移提取和预测

本文采用指数平滑法进行趋势项提取，其中平滑指数a的取值不同分解效果不同，不同a的取值分解效果如图5所示。当a值越趋近于1时，曲线越接近于原始位移，a值越趋近于0时，曲线越平滑。经过测试，当a取0.3～0.6时，周期项的预测效果较好，由图5可知，a在0.3～0.6范围内时，提取出的趋势项仍然呈现明显的阶梯状，因此本文通过多次使用指数平滑法对原始数据进行分解，分解次数越多，提取出的趋势项越平滑，但是周期项的预测效果也会逐渐降低，因此综合考虑预测精度和提取效率，取a=0.35，分3次提取趋势项，其过程为：以G325的累积位移作为原始数据，应用指数平滑法提取趋势项，将所得的数据项作为新的原始数据，再次应用指数平滑法，循环此步骤直到第3次提取，其中平滑初值为前12期数据的算数平均值。每次趋势项提取结果如图6所示。

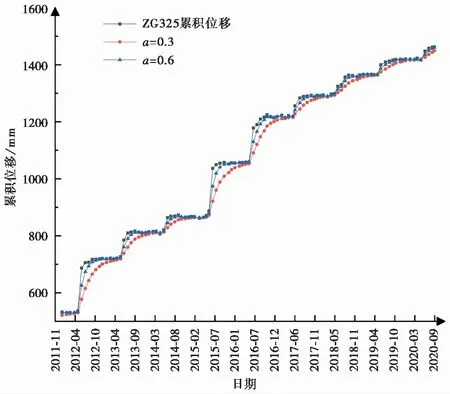
图5 不同a值的分解效果图

图6 趋势项分解结果

将第3次提取的趋势项作为白家包滑坡的最终趋势项，根据图6结果将该曲线分为两段(第1阶段：2012年1月～2015年7月，第2阶段：2015年8月～2019年9月)，分别用3次多项式进行拟合，3次多项式通项公式为：

y=ax3+bx2+cx+d

(10)

直接对第2阶段拟合会导致第2阶段的3次多项式在预测集严重不适应，这是由于过拟合造成多项式曲率偏小或偏大造成的。为了解决这个问题，本文在第2阶段采用K-flod交叉验证的思想，将第2阶段的趋势项位移随机分为5等份(黄光华等，2020)，不重复的每次取其中一份作为测试集，其余4份用来拟合曲线，保留每次拟合曲线的a、b、c、d参数并计算该模型在测试集上的RMSE，计算5次RMSE、a、b、c、d的平均值，多次重复上述步骤，最终取RMSE最小的那一组参数进行拟合。在1000次试验中，获得最佳K-flod交叉验证RMSE为7.331，3次多项式参数如表1第2阶段①所示，用该3次多项式参数预测2019年10月～2020年9月这12期的趋势项位移，获得其RMSE为7.669，预测图像如图7a所示。在非阶跃段，预测绝对误差逐渐减小，在2020年2月达到最小1.120 mm，在阶跃段绝对误差逐渐增大，最大值为13.834 mm。

图7 趋势项位移预测结果

通过上述分析可知，在一次预测12期时，由于缺乏最近的数据对多项式参数进行校正，随着预测期数越多，预测值渐渐偏离真实值，在实际预测中可采用每次预测一期的方法，将上一期的真实值带入训练集校正多项式参数，预测参数如表1第2阶段②。结果表明，在阶跃阶段，预测的绝对误差呈逐渐减小的趋势，其中2020年9月的绝对误差由13.834 mm下降到6.491 mm，而在2019年10月～2020年4月绝对误差下降不大，这说明阶跃阶段的数据对校正起关键作用。

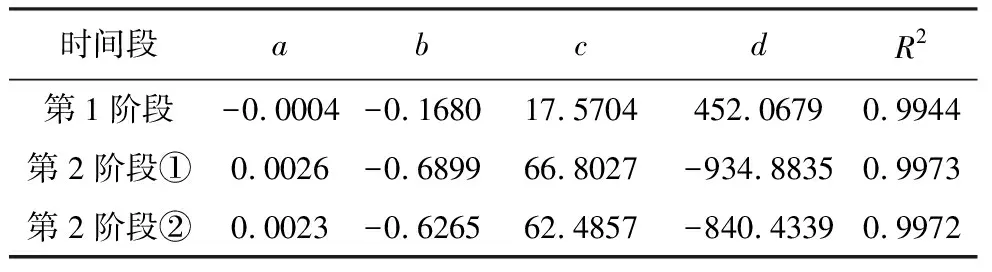
表1 趋势项位移多项式预测参数

3.2 周期项位移提取和预测

3.2.1 周期项位移的提取

将滑坡ZG325累积位移减去第3次使用指数平滑法提取的趋势项，即可获得周期项。如图8所示，所获得的周期项位移在2012年7月和2015年7月有较大增幅，其中2012年7月到2015年6月振幅逐渐减小，到2015年7月振幅突然增大，其后振幅逐渐减小，该规律与ZG325累积位移的阶梯性保持一致。

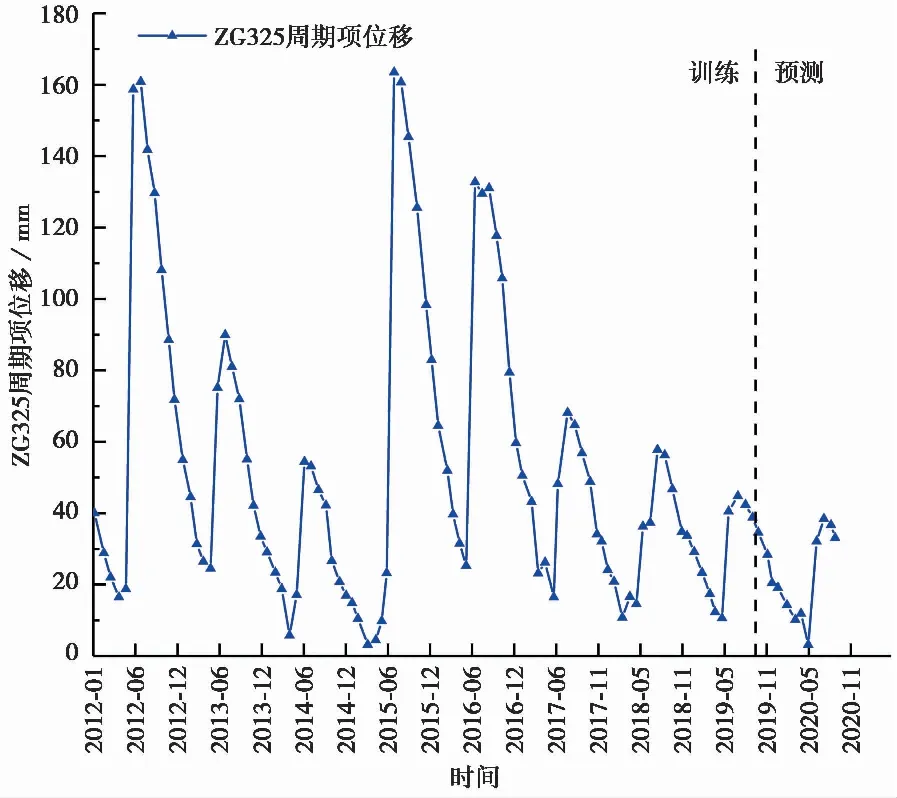
图8 周期项位移提取值

3.2.2 影响因子选取

影响因子的选取对周期项预测起关键作用，好的影响因子能反应预测曲线的走势。白家包滑坡累积位移序列呈明显的阶跃性，这是由于库水位的周期调动和降雨量的联合作用造成的。除此之外，由3.2.1分析可知，累积位移的阶跃性波动也能在一定程度上反应周期项的变化趋势。

3.2.2.1 库水位

库水位调度会改变坡体地下水渗透压力。在库水位下降期间，由于白家包滑坡渗透系数远小于库水位的下降速度，因此产生指向坡外的动水压力，不利于滑坡稳定。本文选取库水位、库水位变化量、两月库水位变化量、库水位下降量、平均库水位、平均库水位变化量、两月平均库水位变化量和平均库水位下降量这8个影响因子。其中平均库水位、平均库水位变化量、两月平均库水位变化量和平均库水位下降量更能总体反应周期项的变化趋势，而库水位、库水位变化量、两月库水位变化量和库水位下降量则更能从反应周期项的细部变化，周期项和库水位关系如图9a。

如图9b，对比当月平均库水位下降量、两月前平均库水位下降量与周期项位移曲线可知，两月前平均库水位下降量的峰值与周期项位移峰值基本保持一致，这不仅说明库水位月下降速率对周期项位移有重要影响，而且表明库水位对周期项的影响在时间上滞后两月。且由图可知，库水位在1～5月逐渐从波峰下降到波谷，6～7月库水位先小幅上升再下降，而滑坡在每年5～9月发生阶跃性位移，1～4月累积位移基本保持不变，也即库水位下降没有立即使1～4月累积位移发生阶跃性变化，这说明库水位对累积位移的影响还存在一个阈值，只有低于这个阈值时才会产生阶跃性位移。从库水位的调度情况来看，当库水位从175 m下降到165 m左右时，其后约两个月，滑坡累积位移将逐渐发生阶跃性跃迁。由于库水位影响因子中有两月因子，考虑到库水位对滑坡位移的综合影响，因此本文将库水位影响因子延后一月，即以一月前的库水位影响因子对当前月位移进行预测。降雨和位移增量对周期项位移的影响在时间上和库水位保持一致，因此将降雨因子和位移增量因子都延后一月。

3.2.2.2 降 雨

根据马锐(2019)对白家包滑坡变形与降雨、库水位相关性定量化分析研究结果，白家包滑坡的变形主要是库水位快速下降造成的，因此本文仅选取降雨量和降雨变化量作为降雨因子。降雨一定程度上会使土体软化，降低岩土体强度，随着降雨量增加，坡体自重逐渐增大，从而引起坡体位移速率增大(吴仁铣，2013)。如图9c可知，强降雨和周期项位移峰值在时间上基本保持同步。

3.2.2.3 位移增量

滑坡累积位移-时间曲线呈阶跃性，并且其阶跃的高度与周期项位移的振幅基本保持一致，说明滑坡累积位移月增长速率和周期项位移有一定的联系，如图9c所示。因此将第2次分解后趋势项的位移增量作为影响因子。

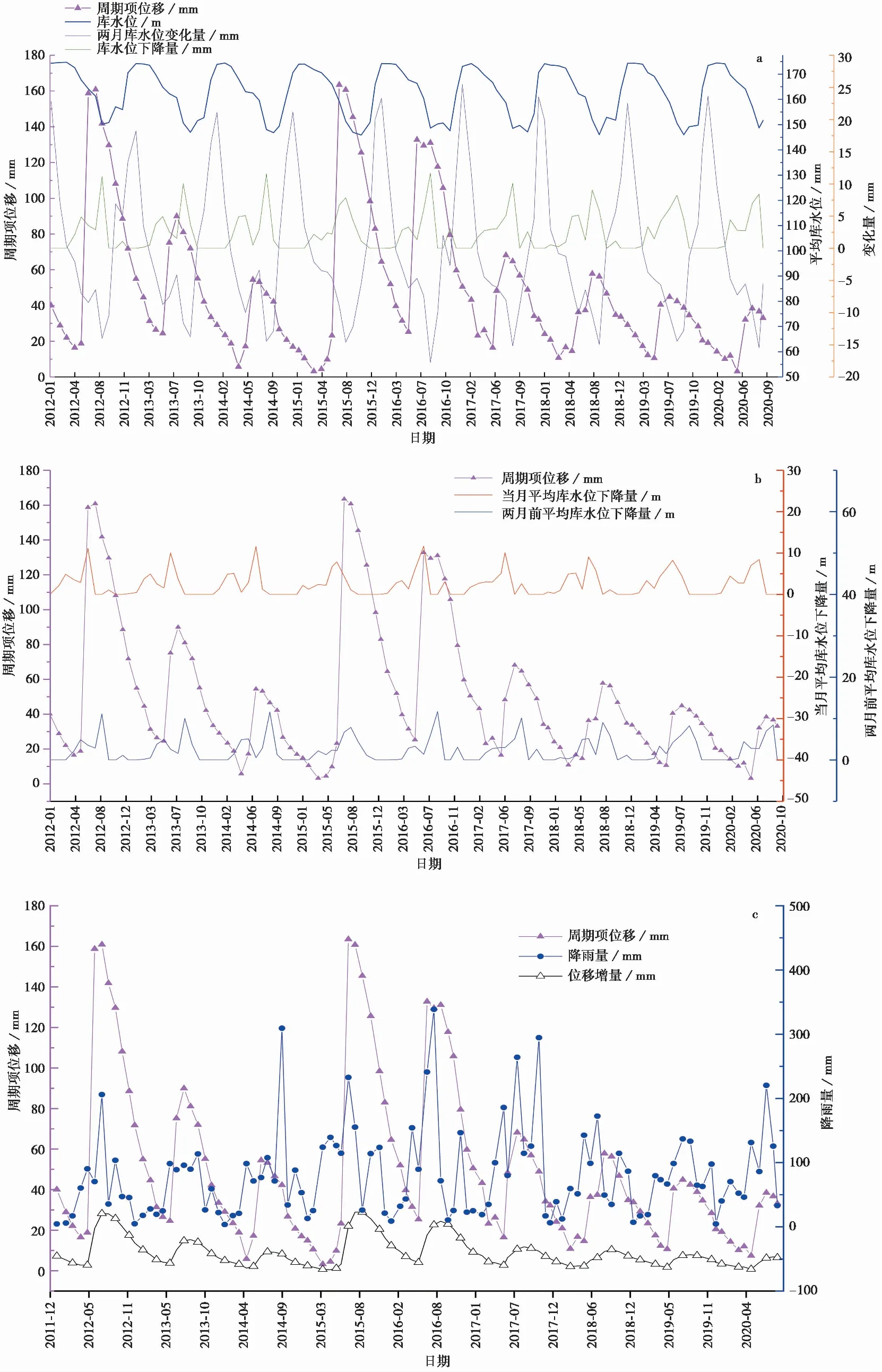
图9 周期项位移与影响因子关系

3.2.3 混合核函数SA-SVR模型预测过程

3.2.3.1 数据预处理

为了消除不同量纲对模型的影响，需要将样本数据进行归一化处理。本文采用Min-Max归一化方法，将影响因子和周期项位移归一化到[0，1]区间内。

3.2.3.2 构造混合核函数

本文通过线性核函数与高斯径向基核函数的线性组合构造混合核函数，通过调整线性指数的数值，以期获得泛化能力和学习能力都较强的SVR模型。试验证明，不同惩罚系数C和核函数参数g下的线性核比例-预测结果RMSE曲线的差别巨大，如图10所示，在参数C=8.15，g=0.89时，预测结果均方根误差先减小，然后逐渐增大；而在参数C=6，g=3时，预测结果均方根误差随着线性指数先减小，再缓慢增大，且最大值与最小值差距较大。这两种情况充分说明线性指数对预测精确度有重大影响。本文以线性核比例控制混合核函数作为SVR模型的优化参数之一，通过模拟退火算法对线性核比例进行参数寻优。混合核函数实现采用MATLAB分析软件，由于LIBSVM工具箱没有现成的混合核函数可以调用，因此需要自己构建混合核函数。

图10 线性核比例与预测结果RMSE曲线图

3.2.3.3 模拟退火算法参数设定及目标函数构造

设定初始温度为100，温度衰减系数为0.9，最大迭代次数为200，每个温度下迭代次数为150，将惩罚系数C、核函数参数g和线性核比例λ构成一个解空间，并设定其上限为[20，10，1]，下限为[1，0，0]，以SVR交叉验证的均方根误差作为目标函数进行参数寻优。

3.2.3.4 混合核函数SA-SVR模型预测

本文取2012年1月～2019年9月样本作为训练集，2019年10月～2020年9月样本作为预测集，应用MATLAB 2018a数学分析软件实现模型预测。将归一化的11个影响因子作为SVM输入向量，周期项位移作为输出向量，SVM固定参数采用LIBSVM工具箱中的默认值，惩罚系数C、核函数参数g和线性核比例λ使用模拟退火算法进行参数寻优，核函数使用混合核函数，在训练集中获得的最佳参数组合为C=8.154，g=0.891，λ=0.460。将该参数带入预测集中进行预测，周期项位移预测结果如图11所示。混合核函数SA-SVR预测模型的判定系数R2和均方根误差RMSE分别为0.791和4.9348，由图11可知，在2019年10月～2020年4月期间，由于累积位移基本保持不变，因此周期项表现为逐渐下降的趋势，在2020年5月～2020年9月，由于库水位下降和持续降雨，滑坡累积位移发生阶跃性跃迁，因此周期项表现为逐渐增大的趋势。模型在2019年10月～2020年4月表现良好，平均绝对误差为2.648 mm，RMSE为3.075。在2020年7月～2020年8月，模型在峰值处预测相较于真实值略高，绝对误差分别为9.99 mm和4.39 mm，表现为预测的结果更加保守，结合2019年10月～2019年12月预测结果可知，模型在峰值后下降速度较真实值更快。

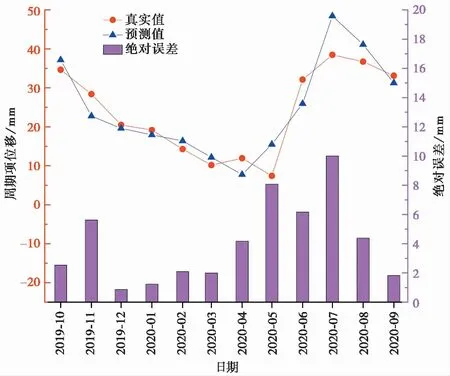
图11 ZG325监测点周期项位移预测结果

3.3 滑坡累积位移预测

将趋势项位移预测和周期项位移预测相加即为累积位移预测，预测结果如图12所示。由图可知，预测结果和真实值基本保持一致，预测阶段判定系数R2为0.790，均方根误差RMSE为8.5877，在阶跃时预测结果较真实值略高，其原因是周期项和趋势项在阶跃阶段预测结果比真实值都偏高。如表2所示，2020年7月出现最大绝对误差，其值为15.831 mm，此时相对误差为1.086%，最小绝对误差在2020年3月，其值为1.699 mm，此时相对误差为0.119%。从整体上看，预测结果在6月会提前靠近阶跃峰值，有一定的预警效果，预测结果在阶跃段略高于真实值，然后在非阶跃段逐渐回落至真实值，因此在实际应用中具有一定的安全保障。

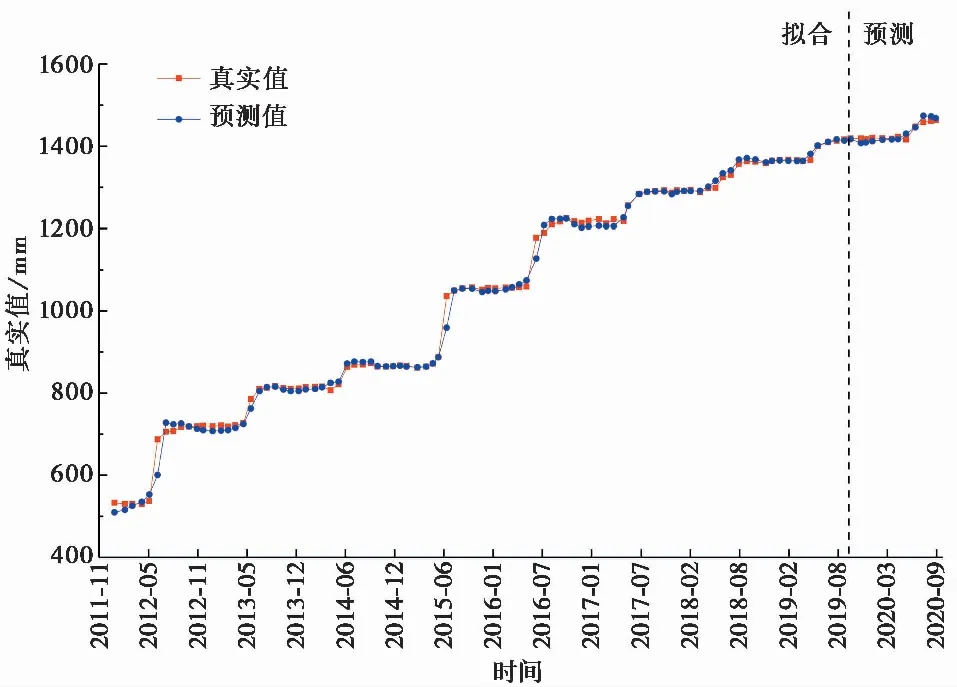
图12 ZG325监测点累积位移预测结果

表2 累积位移预测精度

4 在监测点ZG324上的验证

将基于时间序列分解和SA-SVR混合核函数预测模型应用到ZG324监测点上进行辅助验证，采用K-flod交叉验证思想的3次多项式预测，在2019年10月～2020年9月期间，预测结果的绝对误差呈现先减小后增大的趋势，最大绝对误差发生在12月，其值为9.014 mm，最小绝对误差在4月，其值为0.689 mm，均方根误差RMSE为6.532。通过MATLAB分析软件的LIBSVM工具箱对样本进行训练并通过SA算法对参数寻优，其最佳参数为C=9.963，g=0.957，λ=0.950，最大绝对误差为10.574 mm，最小绝对误差为0.038 mm，均方根误差RMSE为4.559，预测结果在2019年10月～2020年4月效果较好，在2020年5月～2020年8月预测值略高于真实值，并于2020年7月达到峰值，随后预测值逐渐回落，该趋势与ZG325监测点基本保持一致，ZG324监测点趋势项位移与周期项位移预测结果如图13所示。

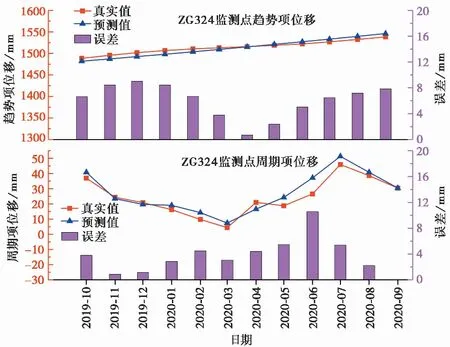
图13 ZG324监测点趋势项位移与周期项位移预测结果

叠加趋势项位移和周期项位移预测结果获得累积位移预测，如图14所示。预测阶段最大绝对误差为15.598 mm，最小绝对误差为0.722 mm，均方根误差RMSE为8.445，并且预测结果在阶跃阶段较真实值略高，有一定的安全保障，该过程与ZG325监测点基本一致，说明本模型具有较强的推广能力。

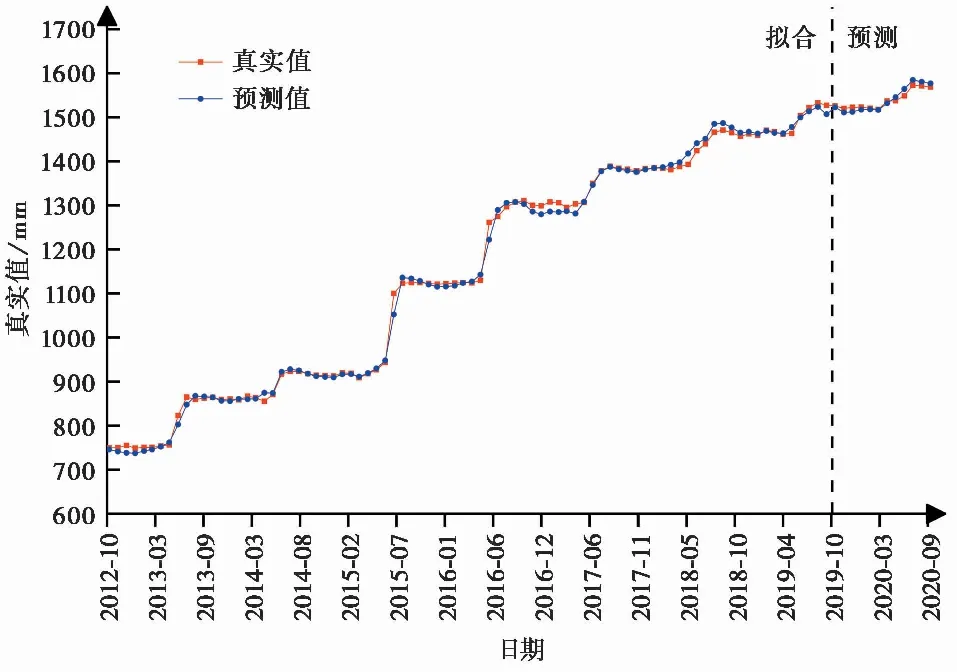
图14 ZG324监测点累积位移预测结果

5 结 论

本文结合时间序列分解和SA-SVR混合核函数预测模型，对白家包滑坡ZG325监测点累积位移进行预测，预测结果与真实值基本一致，其中平均绝对误差为4.016 mm，最大绝对误差为15.830 mm，最小绝对误差为1.699 mm，判定系数R2为0.790，均方根误差RMSE为8.5877，随后采用ZG324监测点进行辅助验证，取得了很好的效果，可以作为同类滑坡监测预警参考模型。

同时，基于本文研究，时间序列与混合核函数SA-SVR的滑坡位移预测模型和传统的时间序列SVR预测模型相比，具有以下优点：

(1)在分解方法上摒弃了传统的移动平均法，采用更适应白家包滑坡阶跃特点的指数平滑分解法，并反复使用指数平滑法使得分解的趋势项和周期项更符合客观规律。

(2)在趋势项预测方法上，采用K-fold交叉验证的多项式参数进行预测，有效缓解了多项式过拟合造成预测值和实际值严重偏离的问题。

(3)针对多参数寻优问题，采用更加高效的模拟退火算法。

(4)在核函数的选择上，不仅仅使用学习能力较强的RBF核函数，而是使用结合RBF核函数和线性核函数的混合核函数，结果表明，混合核函数对周期项预测精度有重要影响。

(5)通过分析诱发因子对周期项位移的滞后关系，以当期影响因子预测后一期周期项位移，从而实现1月内短期位移实时预测，具有较高实用价值。

(6)从预测结果上来看，该模型预测结果在6月会提前靠近阶跃峰值，有一定的预警效果，在非阶跃段预测结果与真实值基本保持一致，而阶跃段的预测结果略高于真实值，然后逐渐回落至与下一阶段非阶跃段高度，具有一定的安全保障。

本模型是建立在白家包多年的滑坡累积位移、降雨量、三峡库区库水位等监测数据上的，由于采用指数平滑法分解的过程中不可避免地损失部分数据，因此该方法在数据较少的滑坡上具有局限性。此外，在参数寻优过程中，训练参数过多会影响计算时间且占用更多内存，参数设置不合理或训练次数不足也可能导致模型输出结果不稳定。