砂土地基中矩形沟槽隔振效果影响区域的试验研究*

2022-05-11刘晶磊梅名彰

工程地质学报 2022年2期

刘晶磊李凯王洋梅名彰

(①河北省土木工程诊断、改造与抗灾实验室，张家口 075000，中国)(②河北省寒冷地区交通基础设施工程技术创新中心，张家口 075000，中国)(③河北建筑工程学院土木工程学院，张家口 075000，中国)

0 引言

随着人类社会经济的发展，轨道交通建设如火如荼，由轨道交通引发的振动不仅对自身运行产生安全隐患，而且对周围环境产生的不良影响越来越明显，许晨等(2018)通过建立动力模型试验，分析了地铁列车振动作用下地裂缝处地层的动力响应规律，研究表明地裂缝活动是影响隧道结构振动的重要因素；高广运等(2014，2016，2019)通过实测上海地铁运行对周围建筑的影响，发现在地铁运行高峰时段会对周围环境振动产生显著的影响，并研究得出了地铁激励作用下地面振动的衰减规律。因此，如何削减振动带来的不良影响已经引起人们的关注，而绝大部分人工振动都可以通过设置沟槽来进行振动隔离。

许多学者对轨道交通振动的沟槽隔振进行了广泛的研究，Woods(1968)通过大量的现场试验研究发现设置沟槽能够有效抑制沟后土体振动。Adam et al.(2005)采用时域耦合边界元-有限元算法、Tsai(2013)采用二维边界元方法、Shrivastava et al.(2002)采用有限元法对冲击荷载作用下空沟及填充沟的隔振效果进行了大量的研究。在国内，李建平等(2020)通过建立有限元模型分析了不同地下水位对沟槽远场隔振效果的影响；姚锦宝(2019)采用理论分析法研究了瑞利波在空沟附近的传播特性，研究表明：增大空沟深度可增强沟后土体振动的衰减；徐斌等(2012)通过2.5D边界元法分析了空沟对移动荷载引起饱和土体振动的被动隔振效果；时刚(2011a，2011b)结合薄层法和边界元法提出以二维饱和半空间薄层法基本解答作为Green函数的饱和土二维频域半解析边界元法；邓亚虹(2007)指出振源距离存在一个最佳位置使得隔震效率最高；孙连勇等(2020)针对机器基础振动，采用现场试验结合边界元分析，研究了空沟几何尺寸对隔振效果的影响；刘晶磊等(2018)通过试验分析认为矩形沟槽对隔振效果的影响与瑞利波的波长有关；徐平(2014)采用数值模拟结合现场试验研究了冲击荷载作用下空沟尺寸以及空沟-荷载间距的隔振性能。

以上对于沟槽屏障隔振效果的研究成果中，主要应用了理论分析和数值模拟等方法，较少将沟槽的振动隔离问题进行平面化、区域化、系统化分析。本文通过现场试验，以矩形沟槽的深度、宽度、长度、振源距离和横截面积为变量，结合不同的瑞利波波长对沟槽的区域隔振效果进行分析，为矩形沟槽的隔振设计提供依据。

1 测试方法

1.1 试验场地及仪器概述

室外试验场地位于郊区，车辆及行人较少，对试验的环境扰动较小，试验场地为4.0im×4.0im×2.0im(长×宽×深)的换填砂性土。如图1所示，试验采用WS-Z30型振动台控制系统，它由控制柜，电磁激励器，计算机和感应器组成。感应器是在测试中应用的11个加速度计，其中一个(0#传感器)位于激振器右侧30icm处用于校核，其他(1～10#传感器)用于流动测试。本次试验的激振波形为正弦波，设置的采样频率以及测量时间分别为5000iHz和5is。

图1 试验仪器及场地

1.2 试验方法及方案

为避免土中杂质对数据采集造成影响，将回填砂过筛且在回填过程中分层夯实，并将土体的含水率控制在12%左右、密度控制在 1.75 g·cm-2左右。如图2所示，在试验场地内部设置一个半径为3im的扇形数据采集区，由于沟槽附近的数据变化较为频繁，数据采集区遵循“前密后疏”的原则分为密集区、次密区和稀疏区3个区域，各区域传感器前后间隔分别为10icm、20icm以及30icm；由图2可以看出，OA轴线为平行于试验场地中线的直线，由于沟槽对称分布在OA轴线上，故扇形采集区为沟槽隔振区域的一半，以O点为圆心，每隔5°设置一条数据采集基准线，在沟槽附近，随着沟槽宽度及长度的变化增加或减少采集点的数量。

图2 测试布局

为了研究矩形沟槽几何参数变化时地表振动变化情况，本文设置了11种不同的试验条件(表1)，变量包括沟深d、沟宽w、沟长l、振源距离e和横截面积n。沟深d表示沟槽的深度，沟宽w表示沟槽的宽度，沟长l表示沟槽的长度，振源距离e表示激振器前端与沟槽中点线之间的距离，横截面积n为矩形沟槽长度与深度的乘积。

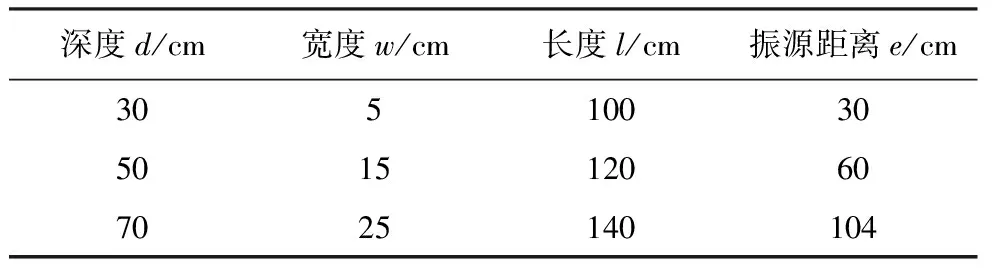
表1 试验参数明细表

2 评价指标

2.1 隔振效果评价指标

如式(1)所示，矩形沟槽的隔振效果采用振幅降低比Ar表示，Ar值小于1则表示有隔振效果。

(1)

式中：a1为有沟槽时控制点的加速度幅值；a0为无沟槽时控制点的加速度幅值。

2.2 参数评价指标

沟槽的几何尺寸对隔振效果的影响与瑞利波波长有着密切的联系(Yang et al.，1997)；为了明确沟槽尺寸和瑞利波波长关系以及它们对隔振效果的影响，引入下列参数进行分析评价。

(2)

(3)

(4)

(5)

N=D×L

(6)

式中：D为深度参数；W为宽度参数；L为长度参数；E为距离参数；N为归一化横截面积(Alhussaini et al.，1991)；λR表示瑞利波波长。

瑞利波波速通过表面波频谱分析方法(吴世明等，1988)测得，经测试计算后得到瑞利波平均波速为VR=109.99im·s-1(刘晶磊等，2018)，波长通过式(7)计算。

(7)

式中：λR表示波长；VR表示波速；f表示频率。

研究认为地铁振动对地面振动影响频段范围为15～200iHz(Sheng et al.，2003)，综合考虑试验参数范围，本文选取30iHz(Liu et al.，2018)(低频)、60iHz(闫维明等，2006)(中频)以及120iHz(高频)3种频率进行研究，由式(7)计算其对应的瑞利波波长，结果如表2所示。

表2 波长明细表

3 试验结果分析

3.1 深度参数对隔振效果的影响

矩形沟槽采用宽度为15icm、振源距离为60icm、长度为120icm，并设置30icm、50icm、70icm 3种深度研究深度参数变化对隔振效果的影响，通过测试指定区域内的加速度幅值，由式(1)绘制隔振沟槽深度参数的振幅降低比Ar值二维等值线图，具体试验工况如表3所示。

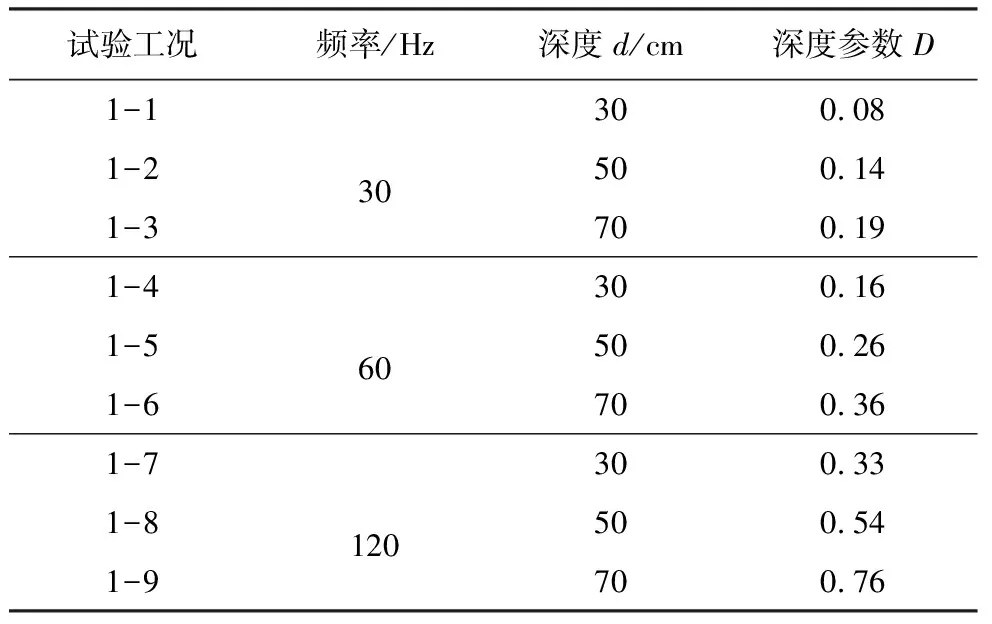
表3 深度参数工况明细表

通过对比各试验工况的隔振效果，以中频60iHz时的等值线图为例进行研究分析(图3)，低频和高频时的等值线图用于参考未在文中给出。

图3 深度参数等值线图

由图3可知，通过设置矩形沟槽，振幅降低比Ar值在沟槽前后出现两种截然不同的情况，在沟前及两侧出现明显的振动加强区域，而在沟后产生明显的隔振效果，这是因为瑞利波在弹性半空间传播时，遇到沟槽屏障会发生能量的重新分配，一部分瑞利波被沟槽反射回去从而增强了沟前的振动强度，另一部分通过沟底和沟侧的绕射以及波的透射突破沟槽屏障的阻隔继续向前传播。

沟后隔振区域的振幅降低比主要集中在0.6以下，Ar值小于0.4区域出现明显的界限范围，并且空沟的最佳隔振效果为60%(徐平等，2015)，故本文以Ar值小于0.4的区域作为振动屏蔽区域以分析沟槽的隔振效果。

比较工况1-4～1-6，矩形沟槽的深度由30icm增加到70icm时，沟前振动加强区域的面积不断增大，该区域的振动强度明显增强，沟后的振动屏蔽区域面积也在不断增大；产生此现象的原因是，沟槽深度的增加，增大了沟槽对瑞利波的阻隔面，更多的瑞利波被反弹回去，通过沟底的绕射波绕射距离增加，加强了瑞利波的耗散。

为进一步研究深度参数对振动屏蔽区域面积S0.4的影响，求得各工况振动屏蔽区域的面积如表4所示，并将各工况的振动屏蔽区域面积与D值进行拟合，得到在不同工况下S0.4与D关系式如式(8)所示，绘制回归方程的拟合图像如图4所示。

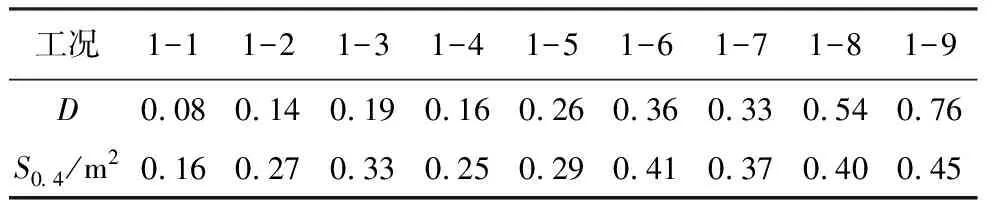
表4 振动屏蔽区域面积一览表

图4 S0.4与D值拟合曲线

S0.4=0.12lnD+0.50R2=0.90

(8)

拟合图像各相关节点的振动屏蔽区域面积S0.4及S′0.4在表5中给出，其中，S′0.4表示增长速率，是振动屏蔽区域面积S0.4与矩形沟槽几何参数拟合曲线在某一点处的切线斜率，S′0.4越小说明振动屏蔽区域的面积变化越不明显。

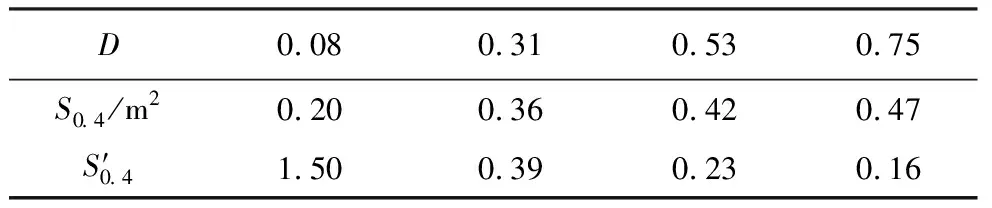
表5 深度参数列表

由图4及表5可知，随着D值不断增大，振动屏蔽区域面积S0.4逐渐增大，增长速率呈减小的趋势：当D值从0.08增加到0.36时，S0.4增大了0.16im2，增长速率减小了1.11，但始终保持在0.39以上，振动屏蔽区域的面积处于快速增长阶段；当D值为0.31～0.53时，S0.4增大了0.06im2，增长速率由0.39降低到0.23，此时，S0.4继续增大，但增加幅度相对减小，处于缓慢增长阶段；当D值为0.53～0.75时，S0.4增大了0.05im2，增长速率低于0.23，振动屏蔽区域的面积变化不大，处于低速增长阶段。

综上所述，深度参数是影响振动屏蔽区域面积的重要因素，在一定条件下，当D值取值范围为0.08～0.53时，随着深度参数的增加，振动屏蔽区域面积显著增大，当D值的范围为0.53～0.75时，振动屏蔽面积变化不明显。

3.2 宽度参数对隔振效果的影响

矩形沟槽采用深度为50icm、振源距离为60icm、长度为120icm，并设置5icm、15icm、25icm 3种宽度研究宽度参数变化对隔振效果的影响，通过测试指定区域内的加速度幅值，由式(1)绘制矩形沟槽宽度参数的振幅降低比Ar值二维等值线图，具体试验工况如表6所示。

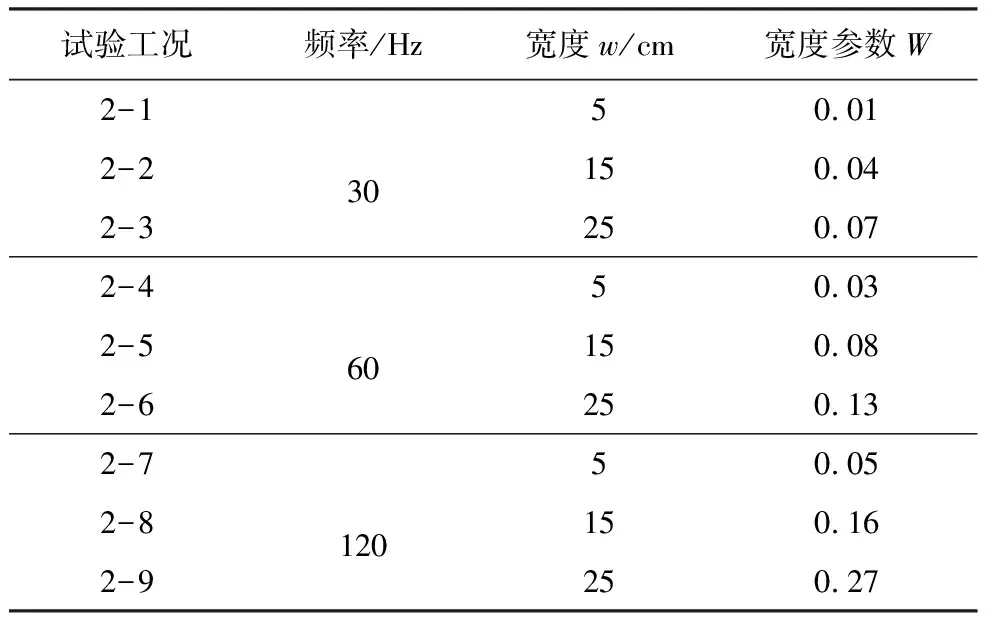
表6 宽度参数工况明细表

同样以60iHz为例进行分析，Ar值等值线图如图5所示，工况2-5的等值线图与工况1-5相同，比较工况2-4～2-6，随着宽度的增加，振动屏蔽区域的面积变化不明显，这是因为增加沟槽宽度主要减弱瑞利波的透射，而试验设置沟槽的宽度变化量为5icm不足最小瑞利波波长的十八分之一，瑞利波透过沟槽的能量差别不大。

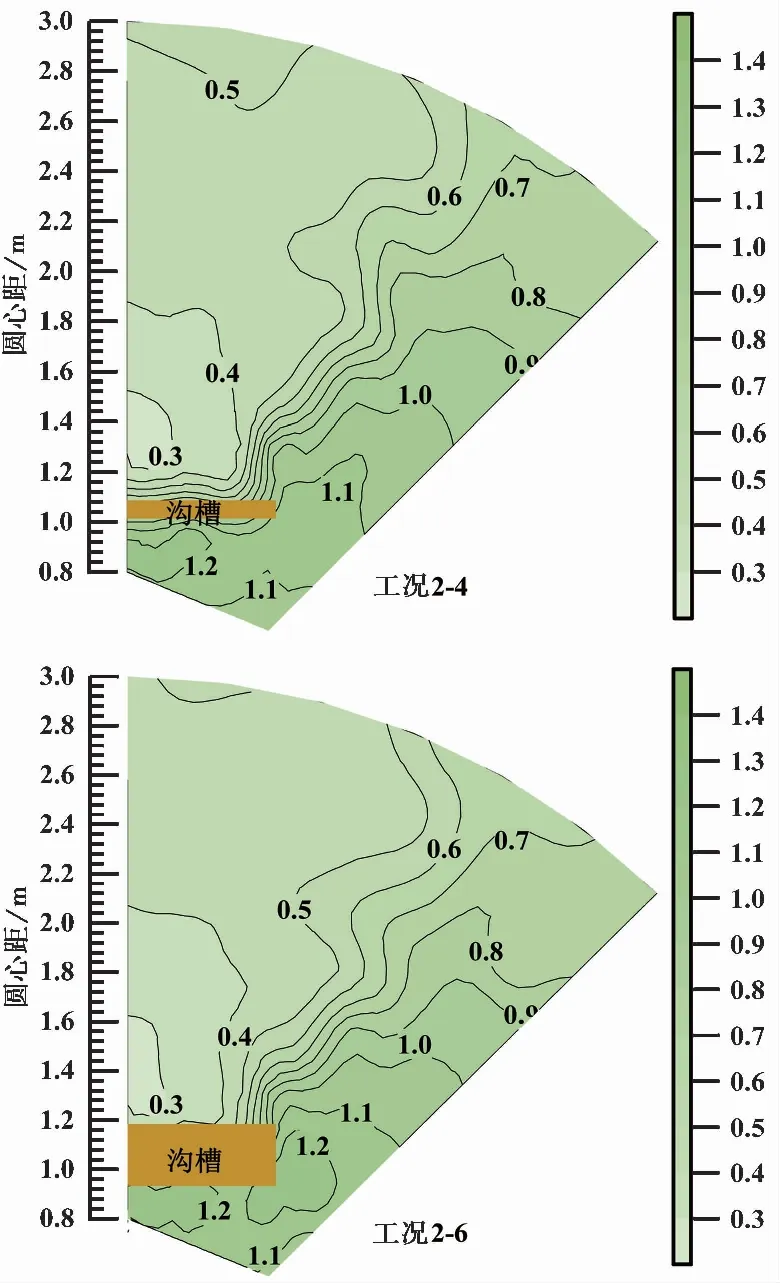
图5 宽度参数等值线图

进一步分析宽度参数变化对振动屏蔽区域面积的影响，求得各工况振动屏蔽区域的面积如表7所示，同样将各工况的振动屏蔽区域面积S0.4与W值进行拟合，得到在不同工况下S0.4与W关系式如式(9)所示，绘制回归方程的拟合图像如图6所示。

表7 振动屏蔽区域面积一览表

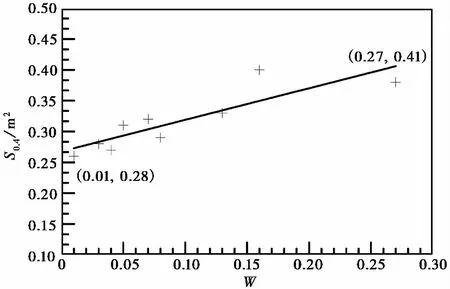
图6 S0.4与W值拟合曲线

S0.4=0.51W+0.27R2=0.75

(9)

由图6及式(9)可知，振动屏蔽区域的面积与宽度参数近似呈线性关系，当W值由0.01增长到0.27时，振动屏蔽区域的面积仅增长了0.13im2，变化不明显。

综上可知，矩形沟槽宽度参数变化对振动屏蔽区域的面积影响较小，一定范围内，增大矩形沟槽的宽度，参数振动屏蔽区域的面积变化不明显。

3.3 长度参数对隔振效果的影响

矩形沟槽采用的宽度为15icm、深度为50icm、振源距离为60icm，并设置100icm、120icm、140icm 3种长度研究长度参数变化对隔振效果的影响，通过测试指定区域内的加速度幅值，由式(1)绘制隔振沟槽长度参数的振幅降低比Ar值二维等值线图，具体试验工况如表8所示。

表8 长度参数工况明细表

综合考察各工况的隔振效果，同样以中频60iHz时的等值线图为例进行长度参数隔振效果分析，如图7所示，其中工况3-5的等值线图与工况1-5相同。

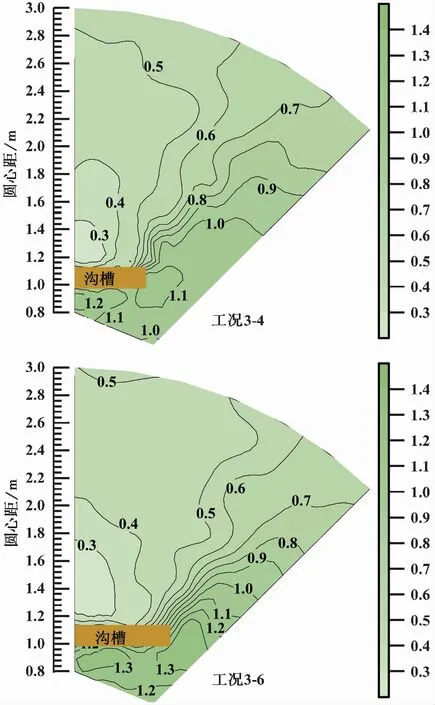
图7 长度参数等值线图

对比工况3-4～3-6可知，振动屏蔽区域的横向延伸范围随着沟槽长度的增加而扩展，振动屏蔽区域的面积明显增大，这是因为瑞利波在传播过程中遇到沟槽时，发生波的衍射现象，随着沟槽长度的增加，阻挡瑞利波传递的阻隔面增大，因此振动屏蔽区域的范围随之增大。

进一步分析长度参数变化对振动屏蔽区域面积的影响，求得各工况振动屏蔽区域的面积如表9所示，将各工况的振动屏蔽区域面积S0.4与L值进行拟合得到在不同工况下S0.4与L关系式如式(10)所示，绘制回归方程的拟合图像如图8所示。

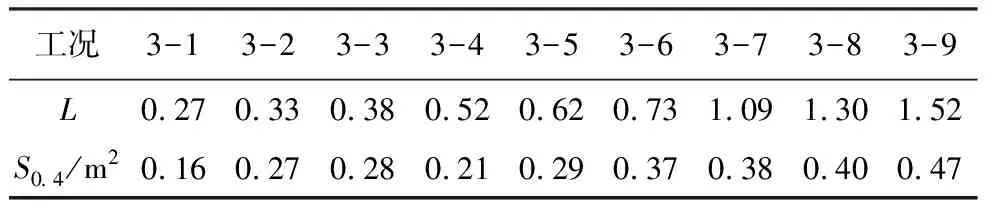
表9 振动屏蔽区域面积一览表

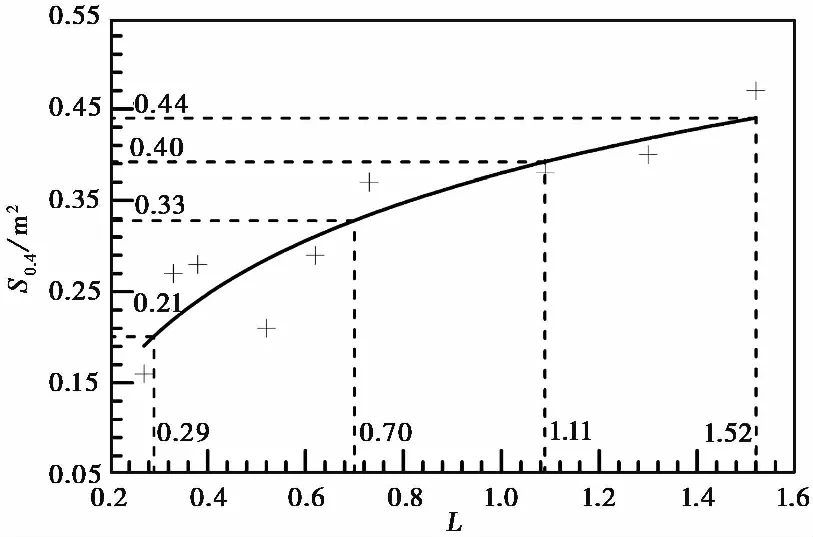
图8 S0.4与L值拟合曲线

S0.4=0.14lnL+0.38R2=0.82

(10)

同样将拟合图像各相关节点的振动屏蔽区域面积S0.4及增长速率S′0.4在表10中给出。

表10 长度参数列表

由图8及表10可知，随着L值不断增大，振动屏蔽区域的面积也在不断增大，增长速率呈现减小的趋势：当L值从0.29增加到0.70时，S0.4增大了0.12im2，增长速率由0.48降为0.20，S0.4处于快速增长阶段，此时，增加长度参数可以显著增大振动屏蔽区域的面积；当L值为0.70～1.11时，S0.4增大了0.07im2，增长速率不断降低且处于0.13～0.20之间，此时，振动屏蔽区域的面积继续增大，但增加幅度相对减小，处于缓慢增长阶段；当L值为1.11～1.52时，S0.4增大了0.04im2，增长速率继续下降且低于0.13，此时，振动屏蔽区域的面积变化不明显，处于低速增长阶段。

综上所述，增加长度参数对振动屏蔽区域面积影响较大；限于本文试验条件，当L取值范围为0.29～1.11时，随着长度参数的增大振动屏蔽区域的面积显著增加，当L值取1.11～1.52时，振动屏蔽区域的面积变化不明显。

3.4 距离参数对隔振效果的影响

矩形沟槽采用宽度为15icm、深度为50icm、长度为120icm，并设置30icm、60icm、104icm 3种振源距离研究距离参数变化对隔振效果的影响，通过测试指定区域内的加速度幅值，由式(1)绘制隔振沟槽距离参数的振幅降低比Ar值二维等值线图，具体试验工况如表11所示。

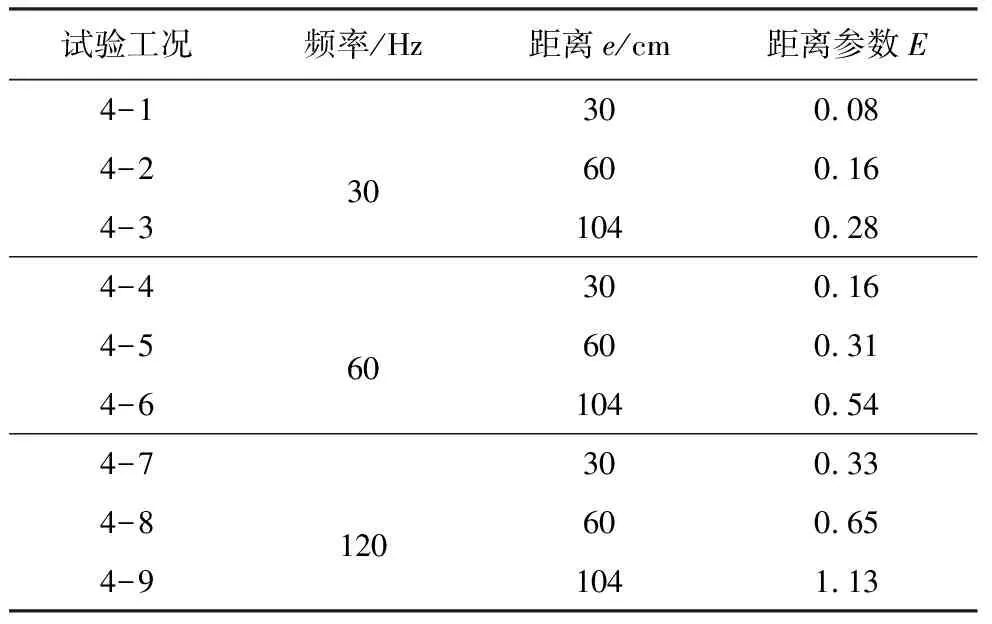
表11 距离参数试验工况明细表

以表11中的工况4-4～4-6为例进行距离参数隔振效果分析，Ar值等值线图如图9所示，其中：工况4-5的等值线图参见图3工况1-5。

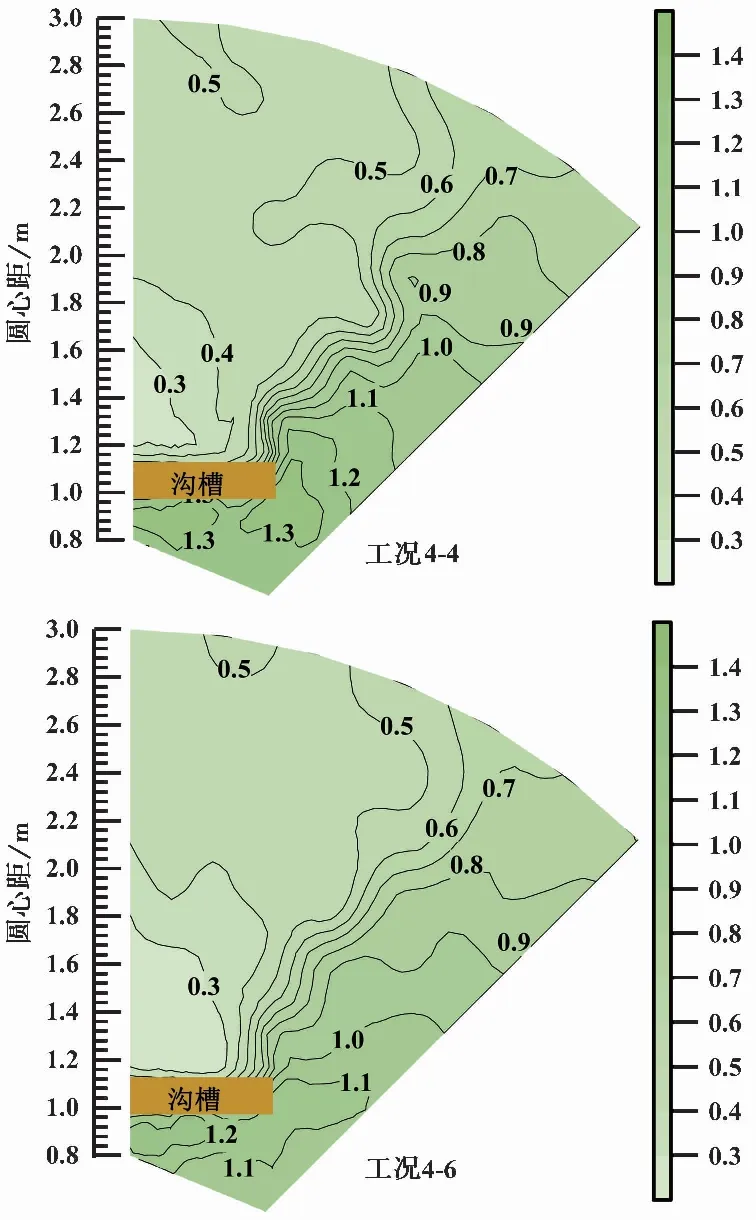
图9 距离参数等值线图

比较工况4-4～4-6可以看出，随着振源距离的增加，沟后的振动屏蔽区域和沟前的振动加强区域产生了明显的变化；对于振动加强区域：随着振源距离减小，振动加强区域的振动强度明显增大，如图9所示，当振源距为30icm时振动加强区域的Ar值基本在1.2以上，而当振源距为104icm时，振动加强区域的Ar值大部分在1.1～1.2之间；这是由于振源较近时，振动强度大沟槽反射较强，从而增强了沟前的振动强度。对于沟后的振动屏蔽区域：随着振源距离的增加，振动屏蔽区域的面积显著增大，原因是，随着振源距离的不断增大，瑞利波在发生绕射前的衰减不断增强。

进一步分析距离参数变化对振动屏蔽区域面积的影响，求得各工况振动屏蔽区域的面积如表12所示，同样将各工况的振动屏蔽区域面积S0.4与E值进行拟合得到在不同工况下E与S0.4关系式如式(11)所示，绘制回归方程拟合图像如图10所示。

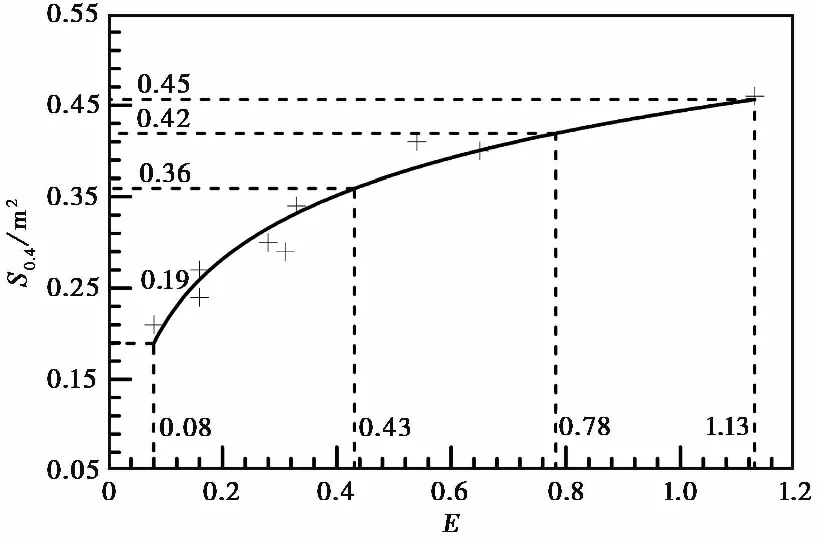
图10 S0.4与E值拟合曲线

表12 振动屏蔽区域面积一览表

S0.4=0.10lnE+0.44R2=0.94

(11)

同样将拟合图像中各相关节点的在振动屏蔽区域面积及增长速率S′0.4在表13中给出。

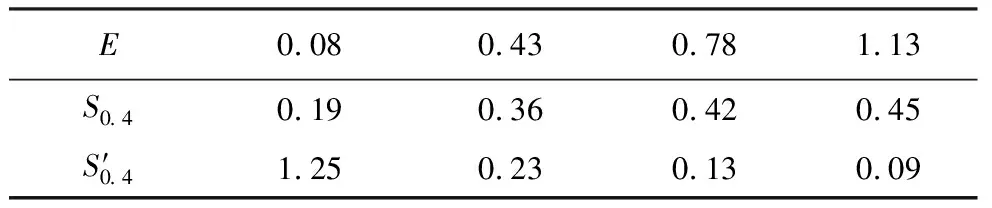
表13 距离参数列表

由图10及表13可知，随着E值不断增大，振动屏蔽区域的面积也在不断增大，增长速率不断减小：当E值由0.08增长到0.43时，S0.4增大了0.17im2，增长速率由1.25下降到0.23，此时，增加距离参数可以显著增大振动屏蔽区域的面积，处于快速增长阶段；当E值为0.43～0.78时，S0.4增大了0.06im2，增长速率继续下降且保持在0.13～0.23之间，此时，屏蔽区域的面积继续增大，但增加幅度相对减小，处于缓慢增长阶段；当E值为0.78～1.13时，S0.4增大了0.03im2，增长速率小于0.13，此时，振动屏蔽区域的面积变化不明显，处于低速增长阶段。

由上述分析可知，距离参数对矩形沟槽振动屏蔽区域面积分布有重要影响；限于本文试验条件，当E取值范围为0.08～0.78时，增加距离参数可以显著增大振动屏蔽区域的面积，当E值为0.78～1.13时，振动屏蔽区域面积变化不明显。

3.5 归一化横截面积对隔振效果的影响

矩形沟槽采用宽度为15icm、振源距离为60icm，并设置0.3im2、0.6im2和0.98im23种横截面积研究归一化横截面积变化对隔振效果的影响，通过测试指定区域内的加速度幅值，由式(1)绘制隔振沟槽距离参数的振幅降低比Ar值二维等值线图，具体试验工况如表14所示。

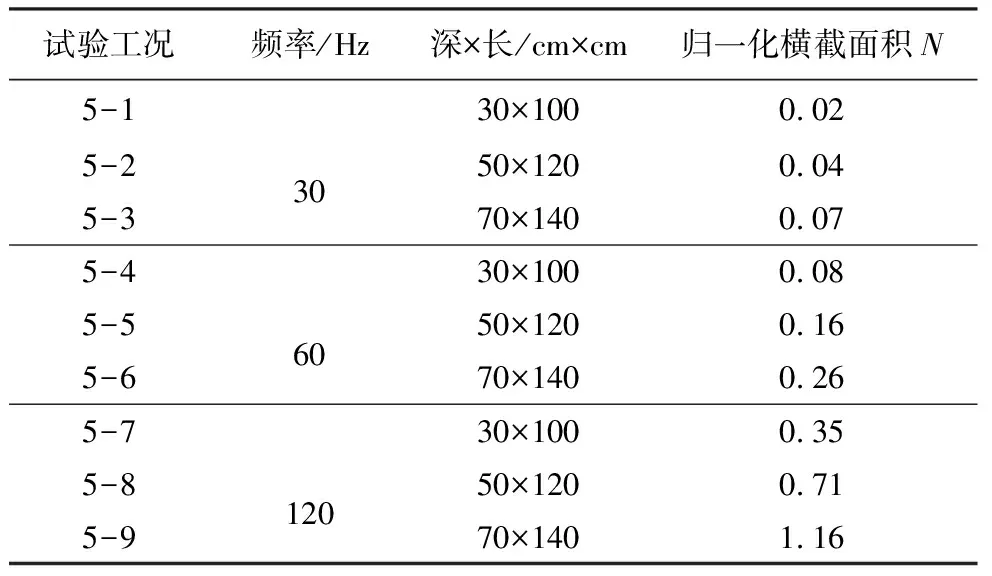
表14 归一化横截面积工况明细表

综合考察各工况的隔振效果，以表14中的工况5-4～5-6的等值线图为例进行归一化横截面积隔振效果分析，如图11所示，其中工况5-5的等值线图与工况1-5相同。

图11 归一化横截面积等值线图

比较工况5-4～5-6可知，随着矩形沟槽横截面积的增加，沟后振动屏蔽区域的面积逐渐增大，隔振效果越来越好，而沟前的振动加强区域的面积和振动强度明显增大；这表明增大矩形沟槽的横截面积可以有效降低瑞利波的绕射并增强瑞利波的反射。

进一步分析归一化横截面积变化对振动屏蔽区域面积的影响，求得各工况振动屏蔽区域的面积如表15所示，同样将各工况的振动屏蔽区域面积S0.4与N值进行拟合得到在不同工况下N与S0.4关系式如式(12)所示，绘制回归方程的拟合图像如图12所示。

图12 S0.4与N值拟合曲线

表15 振动屏蔽区域面积一览表

S0.4=0.07lnN+0.45R2=0.86

(12)

同样将拟合图像中各相关节点的在振动屏蔽区域面积及增长速率S′0.4在表16中给出。

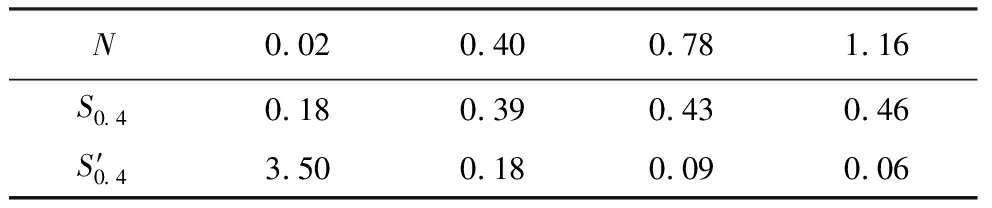
表16 归一化横截面积列表

由图12及表16可知，随着N值不断增大，振动屏蔽区域的面积也在不断增大，增长速率不断减小：当N值由0.02增长到0.40时，S0.4增大了0.21im2，增长速率由3.50骤降到0.18，此时，增加距离参数可以显著增大振动屏蔽区域的面积，处于快速增长阶段；当N值为0.40～0.78时，S0.4增大了0.04im2，增长速率继续下降且保持在0.09～0.18之间，此时，振动屏蔽区域的面积继续增大，但增加幅度相对减小，处于缓慢增长阶段；当N值为0.78～1.16时，S0.4增大了0.03im2，增长速率小于0.09，此时，振动屏蔽区域的面积变化不明显，处于低速增长阶段。

综上所述，矩形沟槽的归一化横截面积对振动屏蔽区域面积分布有重要影响；限于本文条件，当N取值范围为0.02～0.78时，增加距离参数可以显著增大振动屏蔽区域的面积，当N值为0.78～1.16时，振动屏蔽区域面积变化不明显。